光照对赤松生长的影响研究
董兴囤,陈传友,李慧,谢娜,赵燕,房克清
(1.山东省泰安市高新技术开发区良庄镇林业站,山东 泰安 271028;2.泰安市徂徕山林场,山东 泰安 271000;3.泰安市林业局,山东 泰安 271000;4.山东省泰安市岱岳区林业局,山东 泰安 271000;5.山东省林业监测规划院,山东 济南 250014)
影响树木等植物生长的主要自然因素是光照、温度和水,人们也在生产实践中通过对三种因素的调节,而达到较为理想的生产目的,如浇水、抚育、整地、保护地栽培、控光控温调节湿度等。有许多专家学者通过树木历史年轮数据的分析,建立树木生长量与降水量之间的数学方程,进而对历史降水量数据进行了重建,笔者对此也进行了十几年的研究,并取得了较为理想的研究成果。但对于光照而言,可能会起到更为积极的作用,因为水是可以人为调节的,但是光照要做到人为调节,其成本相当高,需要较为复杂的光控技术,对人员也有相当高的技术要求。笔者通过文献检索,很少有这方面的报道,只是局部(主要是花草等)做了许多光照影响试验,也有人做过太阳辐射强度对树木生长的直接影响研究,但是关于对树木生长的历史影响,还没有发现类似报道,笔者从降水量对树木生长历史影响的研究得到启发,利用数学经验方程对这一课题进行系统研究。
1 资料来源
历年日照时数资料由烟台市牟平区气象局提供,由于当地缺少年均太阳辐射强度资料,因此利用历年日照时数对光照对树木的影响进行研究。解析木材料来自2013年3月中旬笔者采自烟台市牟平区昆嵛山林场两株生长正常的赤松解析木,分别为65年生和45年生;风云林场两株生长正常的赤松解析木,分别为77年生和61年生。树高超过10 m的,胸径段用2.6 m区段,其余的采用2 m区段,分别在树高5 cm(0盘)、1.3 m、3.6 m、5.6 m、7.6 m、9.6 m处截取圆盘,树高不到10 m的,采用1 m区段,5 cm(0盘)、0.5 m、1.3 m、1.5 m……9.5 m处截取圆盘,经干燥(风干)、打磨,用高分辨率扫描仪进行彩色扫描,并将扫描好的图像放入CAD操作平台中进行量测,并用实测资料进行校正,分别量取南北径和东西径,并以5年龄阶进行交叉定年,数据精度为0.01 cm,量取各树盘各年度的树木直径,并根据有关测树学技术原理,推算树高和材积。
2 研究方法
经过近10多年来的研究,树木的生长量、生物量、碳储量均与树龄及年日照时数之间表现出十分明显的相关关系,而且凡是线性相关系显著的,其对数值表现更为显著的相关性。经过用指数经验方程y=exp(a+bx)用来判断因变量y随自变量x的变化程度(变化速度),其中y为树木的生长量、生物量、碳储量等指标,x为树龄及年日照时数等自然因素指标,a,b为待求系数(下同)。用混合经验方程y=exp(a-b/x)来寻求效益指标最大化,即用最少的投入(包括时间)以求获得最大的收益。以每一年为研究对象,对方程进行拟合试验,结果除个别指标表现出相关关系显著外,大部分指标相关关系不显著,但是通过累加效应(即用累计生长量与树木年龄、日照时数累加量等建立回归相关方程),则表现出十分显著的相关性,有许多研究人员用5年滑动的办法,使回归相关系数大大提高,事实上就用5年的数据累加,只不过是取了5年的均值而已,事实是这种做法只是提高回归精度的一种办法,其科学含义就不准确了,笔者采用累效应具有十分明确的科学含义。例如树木生长量和树木年龄。树木年龄就时间的累加量,树木生长量累加,即树木总生长量。而用5年滑动的办法处理数据,是用5年的均值代表中间年份的数据指标,是有点牵强附会,用5年滑动的办法,对于首尾两端的数据就不好处理了,因为缺乏数据支撑,但是对于研究上百年上千年的数据变化还是可以的,可以将两端数据舍弃。若充分利用累加效应,不仅弥补了滑动处理数据的不足,而且更能显示其科学含义,计算量相对小一点。
先用经验方程y=exp(a+bt)和y=exp(a-b/t)建立树木生长量与树木生长年龄的回归关系,求得待求系数,再用经验方程y=exp(a+bp)和y=exp(a-b/p)求得树木生长量与年日照时数的回归系数,再用树木年龄的回归方程计算结果对日照时数回归方程进行技术修正,所有过程均要进行检验和校验,然后用校验好的日照时数回归方程,对没有日照时数记载的年份的年日照时数进行重建,进而得出树木整个生长期的年日照时数,进而进行气候干湿周期的研究分析。具体研究过程如下。
3 研究过程
经过研究发现,对于经验方程y=exp(a+bx)的演算,当x的所有数据同时加上或减去同一数值,试验结果只是a值变化,b值和用来检验的t值、F值、R值及试验精度保持不变,因此通过这一方程,来实现以往没有实际记载数据的重建成为可能,而保持现有试验的精度不变。
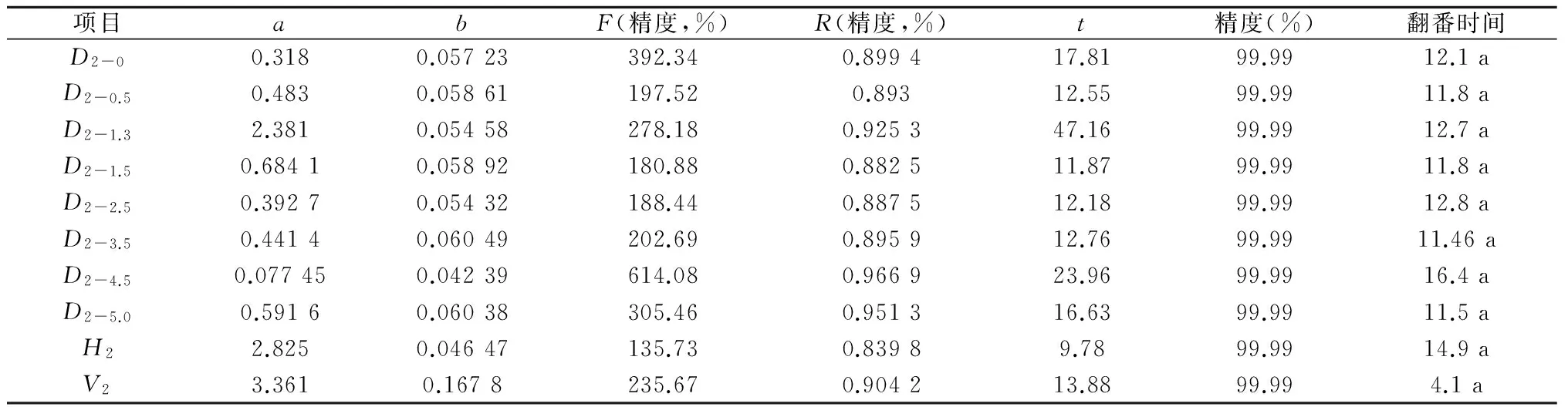
表1 77年生赤松生长过程经验方程拟合表(近42 a) y(t)=exp(a+bt)
以77年生样木为主,对这一科学研究方法进行论述。先用解析木资料建立树木生长量与树木年龄的经验方程。用D2-0代表地径项目,用D2-0.5代表0.5 m高处树径项目,余者类推,用H2代表树高项目,用V2代表树木材积项目。用Y(t)代表以时间(树木年龄)为自变量,以树木各种指标的生长量为因变量的函数。分别利用经验方程y(t)=exp(a+bt) 和y(t)=exp(a-b/t)建立数字回归方程。用电子表格计算,得到试验结果如表1、表2、表3、表4所示。所有项目均通过R检验、F检验和t检验,拟合精度均达到99.99%以上,表3的胸径项目、表4许多项目研究精度无限接近100%。表中的翻番时间为该树木生长量每增长一倍所需时间,用来形象的表达树木生长速度。从表1看出,树木材积增长最快,而表2中看出,树木5.0 m 径增长最快。表3、表4中的tm、tz分别为函数y(t)=exp(a-b/t)的一阶和二阶导数值,前者是在此时刻树木生长指标平均增长速度最大,后者是即时增长速度最大,前者是后者的二倍。试验精度之高,说明选用方法及试验数据的合理性和准确性。
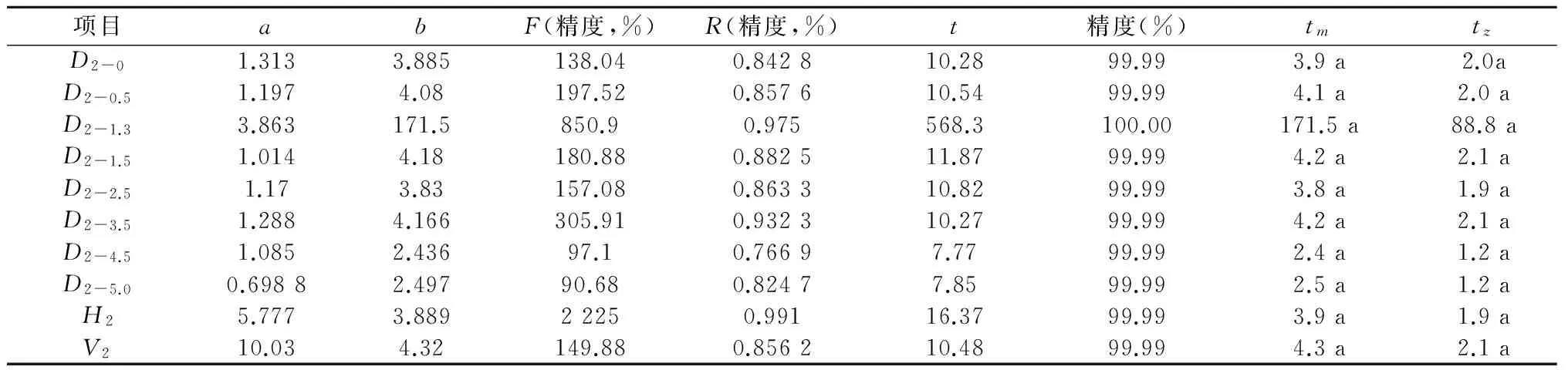
表2 77年生赤松生长过程经验方程拟合表(近42 a) Y(t)=exp(a-b/t)
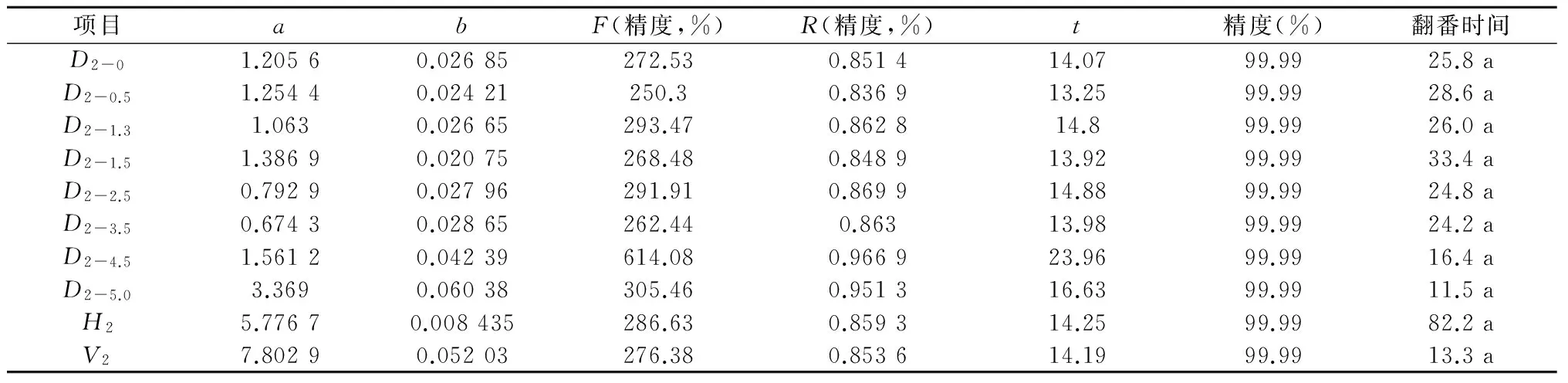
表3 77年生赤松生长过程经验方程拟合表 Y(t)=exp(a+bt)
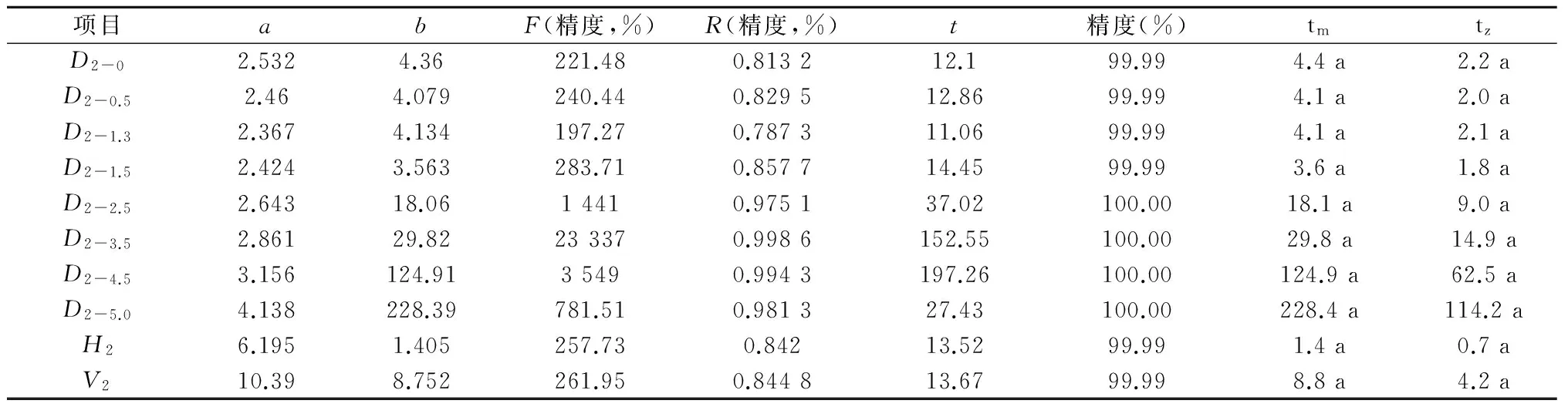
表4 77年生赤松生长过程经验方程拟合表 Y(t)=exp(a-b/t)
以同样的方法进行赤松生长量与日照时数经验方程的拟合试验,试验结果详见表5、表6。试验结果均未出现异常现象,均具有一致性,说明试验结果稳定可靠,试验精度达到99.99%以上,表5和表6的几个项目的试验精度无限接近100%。
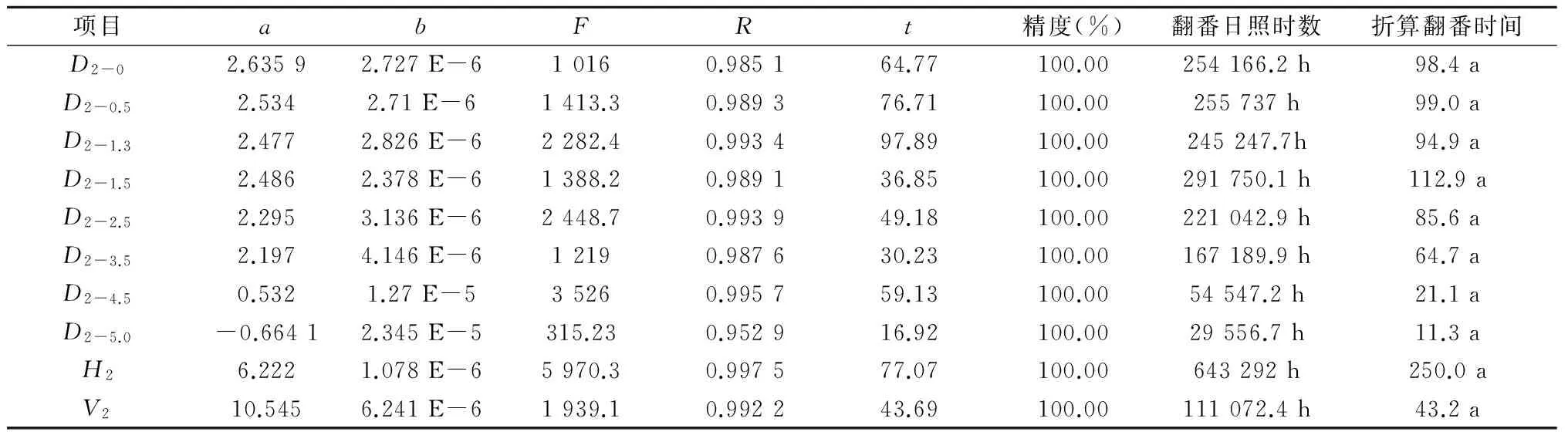
表5 77年生赤松生长量与日照时数经验方程拟合表(近32 a) Y(p)=exp(a+bp)
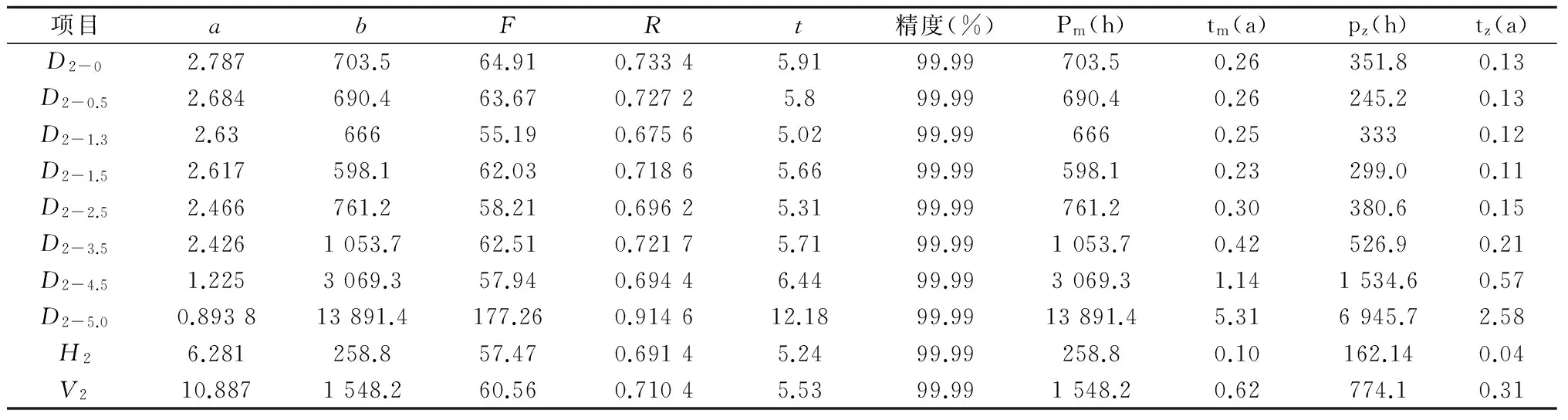
表6 77年生赤松生长量与日照时数经验方程拟合表(近32 a) Y(p)=exp(a-b/p)
为了进一步提高研究精度,以期求得日照时数相对于树木年龄的树木生长影响贡献率,对日照时数拟合经验方程进行校正,就是直接利用树木生长量的对数值与树木年龄经验方程拟合结果得出的树木生长量的对数差值为因变量,以降水量数据为百变量,重新建立经验方程进行拟合试验,
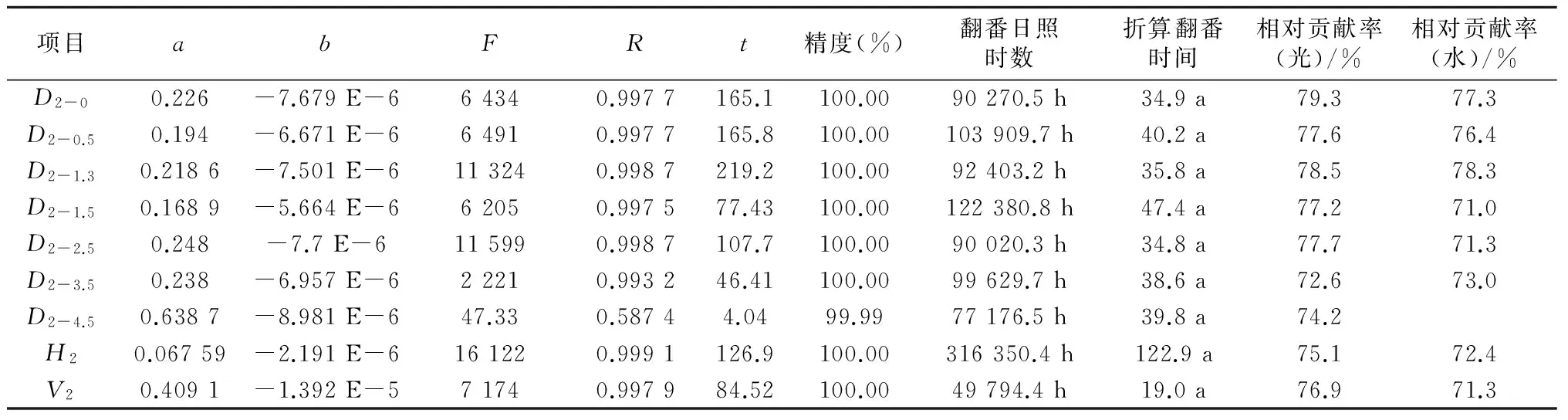
表7 77a生赤松生长量与日照时数经验方程拟合校正表(近32 a) Y(p)=exp(a+bp)
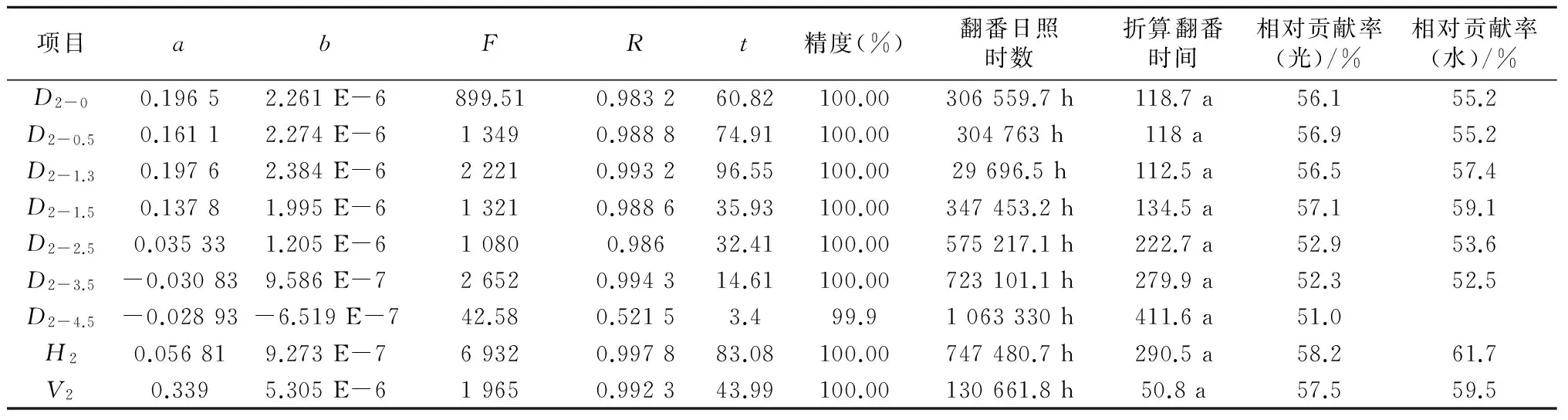
表8 77年生赤松生长量与日照时数经验方程拟合校正表(近32 a) Y(p)=exp(a+bp)
试验结果见表7、表8。表7是利用树龄指数经验方程的拟合结果的对数与树木生长量的对数差值为因变量Y(p),表8是利用混合经验方程拟合结果进行同样的试验。由于由此得出的混合函数方程试验精度很低,笔者不再在表中列出,只有D2-2.5和H2项目表现出接近100%的准确性。在校正试验中,只是列出试验精度相对较高的项目。从表中可以看出,试验结果除个别项目外,实验精度均无限地接近100%,因此可以付诸应用。从函数曲线的发展态势可以看出,由于所有研究指标的非负性,指数函数方程y=exp(a+bx)是研究y随x的增长的趋势,混合函数方程y=exp(a-b/x)是研究y随x的下降的趋势,由于直接用的后近42 a的日照时数数据资料进行的赤松生长量和日照时数之间的拟合试验,由于缺少前35a的降水量资料,而生长量又是整个年份的累加,因此表8中的b值为负值,翻番日照时数事实上也是负值,指的是下降一番(即下降50%)的日照时数,改为正值就是翻番日照时数了。再以表8中的D2-0项目介绍一下相对贡献率的计算。这里的折算翻番时间为34.9 a,可以理解为是扣除了树木生长曲线(S型)特性影响以后的数值,它与表3中同一项目指标25.8 a的差值9.1 a,也就是树木本身生长特性比日照时数单独影响提高了3.6 a,所以该项目的相对贡献率为1÷[1+(9.1÷34.9)]=79.3%。用同样的方法计算出其他项的想对贡献率。从计算结果可以看出降水量对树木生长量影响的相对贡献率,表7数值在71.0%~78.3%,表8数值在55.2%~61.7%,数值指标变化幅度不大,表现稳定,两表之间的数值相差12%左右,可能是由于研究精度的差别造成的,从表7可见精度较高,可靠性大。因此日照时数对树木生长量影响权重达到85%左右,可见研究日照时数对树木生长量影响是何等的重要。相对贡献率又可称作该因素的增益率。从表8中可以看出,光照增益率与降水增益率相比基本持平。
4 试验方程的适用性检验
用同样的方法对另外三株样木进行了试验,取得了较好的试验效果,以此三株样木试验结果对以上的试验结果进行适合性检验。检验结果如表9所示。表中FZ-1与FZj-1分别代表指数方程树龄因素校正前后与1号样木比较的F值,FH-1与Fhj-1分别代表混合方程树龄因素校正前后与1号样木的F值,D0代表地径项目,余者类推。
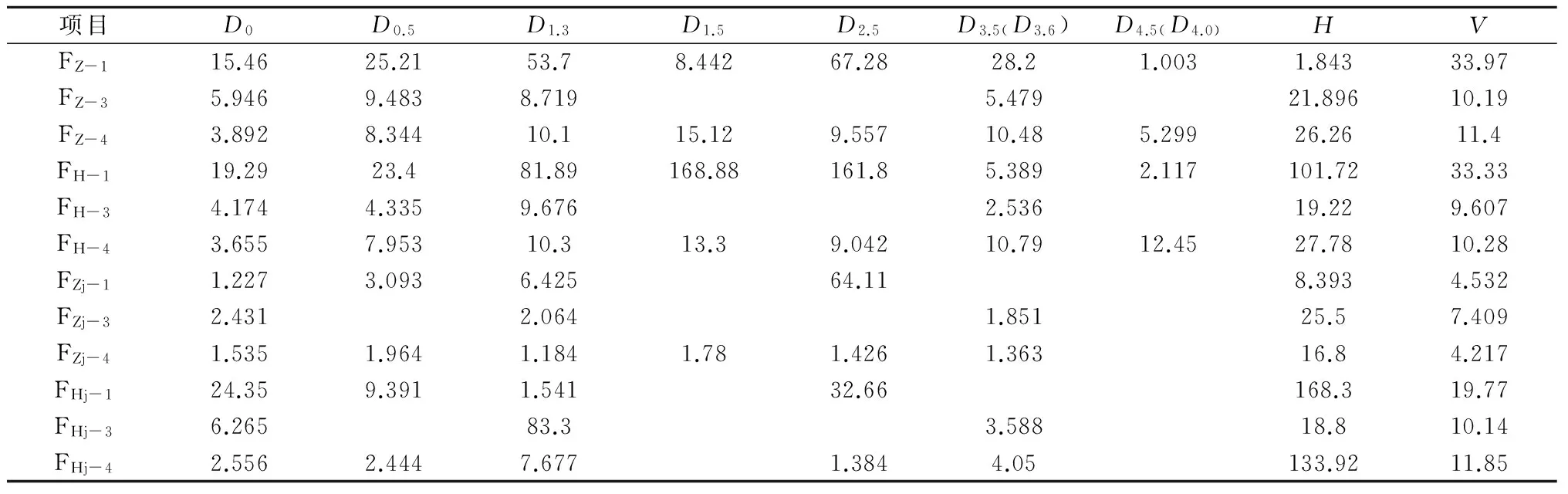
表9 经验方程适合性检验表
通过查表,F0.05-30(可靠度95%,自由度30的F值)为1.84,在表9中,凡是高于这一数值的,就算未通过适应性检验,只有校正后的数据试验部分通过了检验,从中可以看出年龄相近的样木更容易通过适用性检验。因此经验方程系数不能借用,必须在条件具备的条件下重新方程拟合试验,直到通过适应性检验为止。
5 讨论
先前许多学者大部分是利用孤立的树干圆盘,利用年轮测量仪器对年轮宽度进行了测量,是利用多个树木圆盘进行扫描,并在CAD状态下进行判读,利用实测数据进行校正处理,认为本人所进行的实验更具有科学合理性,节省了研究成本的投入,起到了事半功倍的作用,认为并不是实验数据小数点位数越多越好,因为年日照时数数据为4位有效数字,树木直径的测量保留4位有有效数字(即精确至0.01 mm)即可。有的学者精确至0.001 mm,如果是对于生长特别慢的红木等我认为是有必要的,但是对于其他树木就没有必要了,这样可以省下许多工作量,在CAD状态下进行判读,可精确至小数点后若干位,为了节省工作时间,只保留了4位有效数字。通过研究,科学回答了经验方程的科学含义,指数方程即呈指数增长,也就是递增的意思,是树木生长上升潜力的表达式,反映出树木生长的速度问题;而另一混合方程则是树木生长下行压力的表达式,它揭示了效益最大化问题。通过对树木自身增长潜力作用的剔除,而得到光照对于树木生长的相对贡献率,从增长潜力看,相对贡献率均值为74.1%,从增长的下行压力看,相对贡均率均值为55.4%,二者的中值为64.8%,这就是说树木的生长相对于树生长特性来说,光照对树木生长的影响起到65%左右的影响,树木本身特性仅占35%左右,因此研究光照对树木生长的影响是何等的重要,对于我们合理组织林业生产具有十分深远的现实意义。光照和降水对树木生长的贡献率大体相等,说明光和水对树木生长的影响具有同等重要作用,可能与光合作用的机理光解水有关,但是这个作用还得在一定温度下进行,至于温度对树木生长的影响有待于将另立课题进行研究。
[1] 廉丽姝,李为华,朱平盛.山东近40年气候变化特征[J].气象科技,2006,34(1):57-59
[2] 高卫东,袁玉江,张瑞波,等.树木年轮记录的天山北坡中部过去338a降水变化[J].中国沙漠,2011,31(6):1535-1540
[3] 刘国杰.注册咨询工程师(投资)执业资格考试教材复习指导[M].天津:天津大学出版社,2003

