水平井多段压裂非常规裂缝压力动态特征
王镜惠,梅明华,梁正中,王华军,刘娟
随着老油田产油能力不断下降,水平井水力压裂对于提高油井产量具有重要意义,通过水平井水力压裂,将原来井筒附近地层流体的径向流变为线性流,从而减小流体的渗流阻力。随着压裂技术的不断进步与完善,水平井压裂技术在开采致密油气藏中具有广阔的前景[1-6]。地层条件的复杂性以及压裂过程中出现的特殊情况,导致裂缝关于井筒不对称,因此求解压裂水平井压力的核心问题在于多条裂缝压力的相互叠加。在压裂直井压力动态分析方面,国外学者进行了大量研究,文献[2]和文献[3]将储集层渗流压力解与裂缝渗流压力解进行耦合,获得储集层和裂缝渗流系统的井底压力半解析解;文献[6]基于椭圆渗流建立了有限导流垂直裂缝试井解释模型,该模型的优点在于求解速度快,缺点是不能很好地对不对称有限导流垂直裂缝进行研究;文献[7]建立了不对称垂直裂缝试井解释模型,但该模型只描述了裂缝渗流特征,没有对裂缝和储集层渗流井底压力进行耦合求解;文献[8]利用数值模拟方法,对不对称垂直裂缝进行研究,分析了不对称因子对压力导数曲线的影响,但数值模拟计算速度慢。中国学者对不对称垂直裂缝的试井工作做了大量研究,为非常规多段压裂水平井试井模型的研究奠定了基础[9-14]。在水平井多段压裂非常规裂缝试井解释模型的研究方面,文献[15]和文献[16]提出了Laplace空间点源函数理论,对点源函数积分获得单条裂缝无限导流的线源解与面源解,通过压降叠加原理,获得水平井多段压裂非常规裂缝试井解释模型半解析解;文献[17]—文献[19]基于前人的研究,建立了对称裂缝水平井多段压裂试井解释模型,并进行求解;为了提高计算速度,文献[20]在文献[6]的研究成果中引入了裂缝导流能力函数,对无限导流井底压力解与导流能力函数组合,得到有限导流垂直裂缝井和水平井多段压裂井底压力计算的新方法,但该计算方法是基于多条对称裂缝的研究,没有考虑裂缝不对称对试井曲线的影响。在前人研究的基础上,本文建立均质地层单条有限导流不对称裂缝试井解释模型,利用Laplace变换获得其半解析解,然后通过压降叠加原理得到水平井多段压裂井底压力半解析解,最后利用Stehfest数值反演方法[21-22]绘制井底压力和压力导数曲线,并分析不对称因子、裂缝条数、裂缝分布方式和裂缝导流系数等因素对试井曲线的影响。
1 单条有限导流垂直裂缝压力动态特征
1.1 单条有限导流垂直裂缝试井模型
不对称垂直裂缝就是一条或多条水力压裂裂缝,以井筒为中心,裂缝两端关于井筒不对称。为了更好地建立不对称垂直裂缝试井解释模型,根据对称垂直裂缝试井解释模型的建立,以裂缝中点为中心建立直角坐标系,井偏离裂缝中心位置的位移为xw,储集层上下为不渗透边界(图1)。根据文献[15]给出的无限导流垂直裂缝试井解释模型解,结合不对称垂直裂缝试井解释模型,将裂缝与储集层渗流进行耦合,从而求得单条不对称有限导流垂直裂缝井底压力。模型基本假设条件如下:压裂裂缝两端没有流体通过;流体在储集层和裂缝中的流动符合等温达西渗流规律;裂缝宽度为bf,裂缝穿过整个地层;整条裂缝中压力不相同,即沿裂缝有压降产生,裂缝的渗透率为Kf;忽略毛细管压力和重力的影响;储集层流体为微可压缩单相流体。
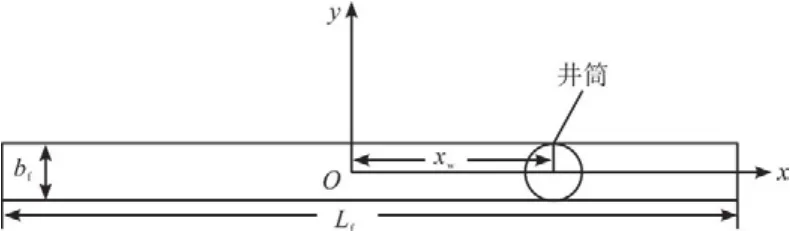
图1 单条有限导流不对称垂直裂缝示意
无量纲变量和不对称因子分别定义为

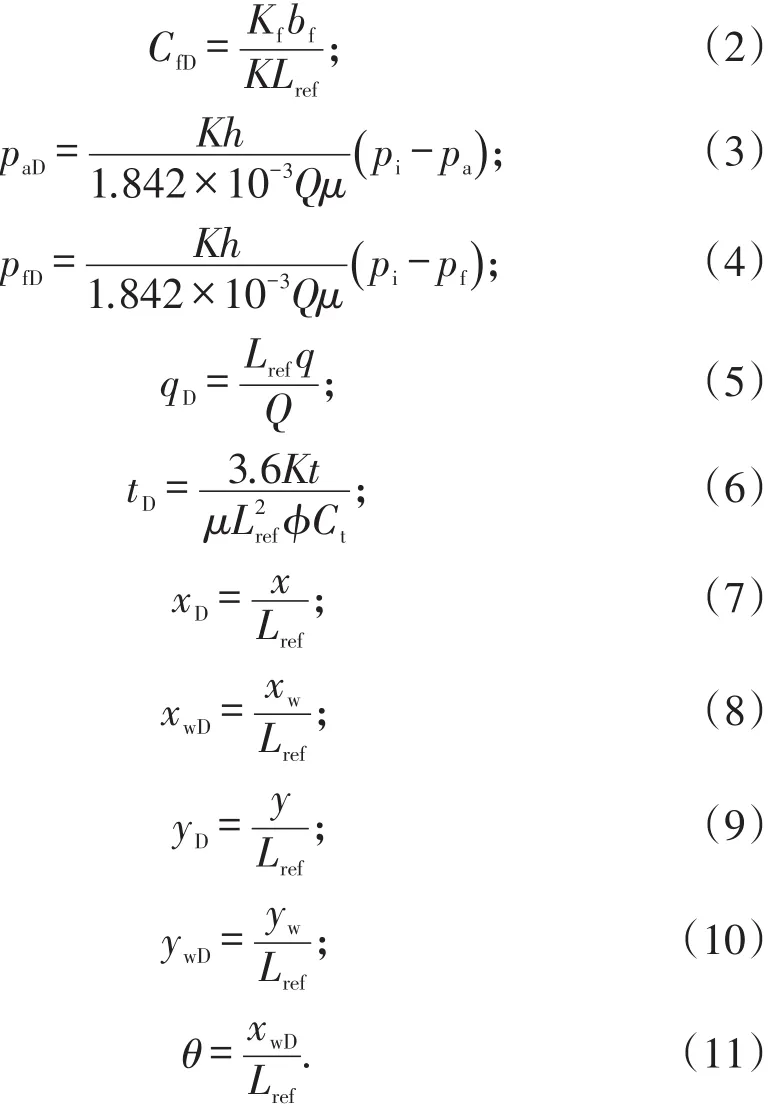
根据上述假设条件,得到无量纲裂缝试井解释模型为
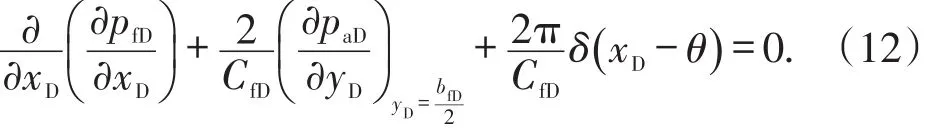
无量纲裂缝试井解释模型的边界条件为

通过使用Laplace变换和Green函数,并联合边界条件(13)式和(14)式,求得(12)式的解为
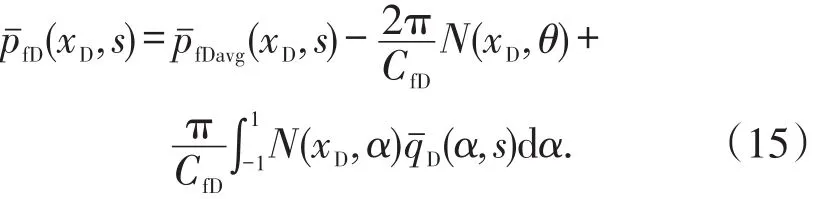
Laplace空间下裂缝平均压力可表示为

根据文献[7],Green函数可以写为

文献[15]和文献[16]对单条无限导流垂直裂缝做了研究,任意地层压力的表达式为

根据裂缝壁面处压力相等,联立(15)式和(18)式,可得无量纲单位长度裂缝流量与Laplace空间下无量纲裂缝平均压力方程:
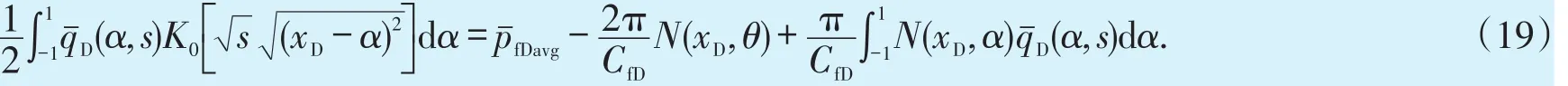
根据质量守恒原理,则无量纲单位长度裂缝流量满足表达式

1.2 裂缝离散化处理
对于有限导流垂直裂缝,流体沿裂缝流动方向存在压降,裂缝不同位置处流量不恒定,而是与位置有关的函数,因此,在计算流量过程中将裂缝进行离散,单位长度裂缝流量可以视为一个定值,对于多条裂缝,根据压降叠加原则,(19)式和(20)式经过离散化处理之后得到:

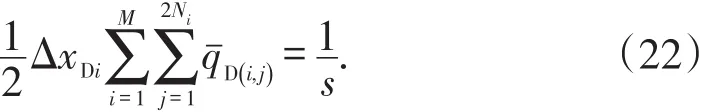
对于单条裂缝而言,M=1,ymD(i,j)=ywD(i,j),(21)式和(22)式构成2N+1个方程组,需求解出qˉD()i,j和pˉfDavg,共有2N+1个未知数,其中Bessel函数的积分可以通过高斯-勒让德数值积分获得,将所求未知参数代入(15)式,并取xD=xasmy,获得井底压力。
根据杜哈美原理,考虑井储和表皮效应的影响,得到的井底压力为[17]

根据(21)式和(22)式,采用Stehfest数值反演方法,绘制有限导流不对称垂直裂缝无量纲井底压力、压力导数与无量纲时间的关系曲线(图2)。将本文所获得的有限导流不对称垂直裂缝无量纲井底压力及压力导数结果与文献[8]中利用数值计算方法得到的结果进行对比,从图2可以看出,利用本文计算获得的结果与文献[8]中的结果符合率高。因此,关于不对称裂缝试井解释模型的研究,可以采用本文解析法代替数值差分求解方法,在数值反演的过程中,以向量为基本运算单元,采用并行算法,提高计算速度。

图2 有限导流不对称垂直裂缝无量纲井底压力曲线(不对称因子为0.6)
2 多条非常规裂缝压力动态特征
对于多段压裂水平井,当开井投产时,M条裂缝同时生产,M条裂缝之间的相互影响可以通过叠加原理得到,应用前面研究结果,对每条裂缝的压降进行叠加,获得所有裂缝的压力。根据文献[19]和文献[20]可知,当裂缝导流系数大到一定程度时,不对称因子变化几乎不影响压力和压力导数曲线形态,然而流体在井筒中的流动被视为无限导流,即井筒导流能力为无限大。因为裂缝不对称是相对于井筒而言,并且每一条裂缝与井筒都存在一个交点,这个交点可以被视为“井筒”,交点两端裂缝长度不相等,根据压裂水平井渗流方式,储集层流体首先从地层流入裂缝,再经过裂缝流入井筒,因此,可以将水平井井筒在x-y平面内弯曲而不改变原有的渗流方式。为了利用不对称因子建立水平井多段压裂非常规裂缝试井解释模型,将多段压裂常规对称裂缝与水平井的交点沿裂缝方向平移,实现裂缝关于“井筒”不对称,所以,可以采用井筒弯曲来进行水平井多段压裂非常规裂缝试井解释问题的研究(图3)。

图3 水平井多段压裂非常规裂缝示意
对于M条裂缝,共有2NM+1个未知数,联立质量守恒方程构成2NM+1个方程组,通过该方程组可以求得2NM+1个未知数,将其代入(15)式,得到井底压力。(19)式可以写成以下矩阵形式:
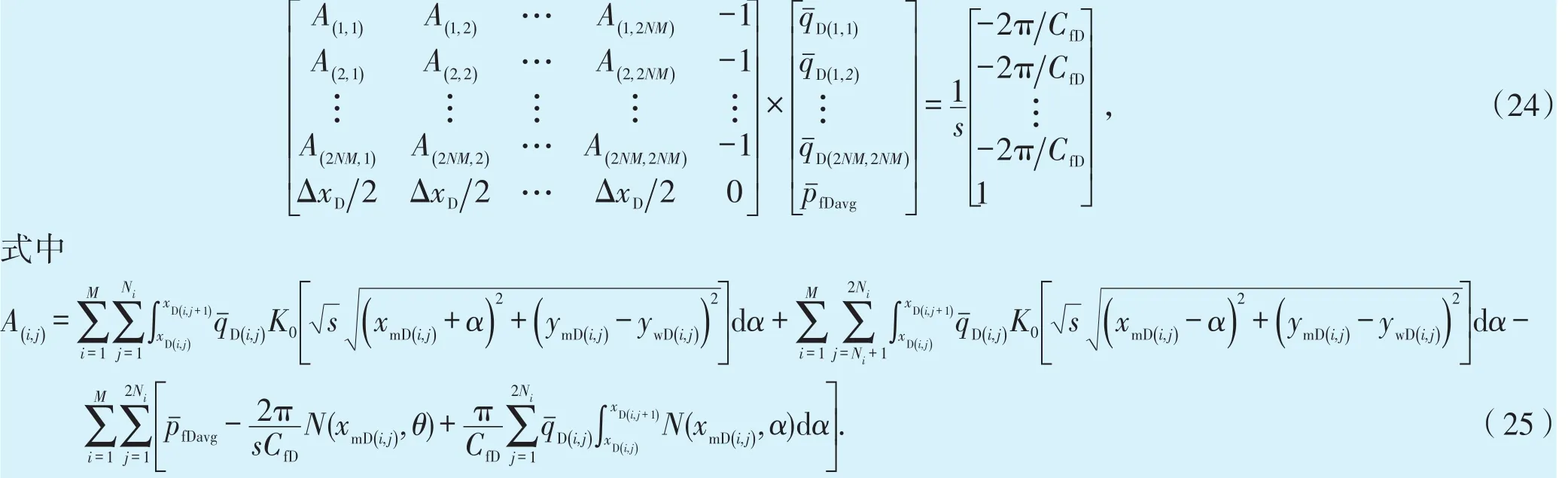
3 试井曲线与影响因素分析
利用Stehfest数值反演方法,对(24)式进行编程计算,得到不考虑井储和表皮效应的井底压力曲线,再根据(23)式,绘制考虑井储和表皮效应的压力和压力导数曲线。
3.1 试井曲线分析
水平井多段压裂非常规裂缝试井曲线[23-24]可分为7个阶段。
(1)井储阶段 纯井储阶段压力和压力导数重合,其曲线斜率都为1.00.
(2)双线性流阶段 沿裂缝流动的线性流和沿垂直裂缝方向的线性流,压力导数斜率为0.25.
(3)早期线性流阶段 只有地层中的流体向裂缝发生线性流,压力导数曲线斜率为0.50.
(4)第一径向流阶段 地层中的流体围绕单条裂缝产生径向流,压力导数曲线斜率为0.
(5)第二线性流阶段 流体沿垂直于井筒的方向发生线性流,压力导数曲线斜率为0.50.
(6)过渡流阶段 压力导数曲线斜率为0~0.50.
(7)系统径向流阶段 地层中的流体沿裂缝和井筒所组成的系统发生径向流,压力导数曲线斜率为0(图4)。图4中无量纲井储系数为0.000 8,表皮系数为0.01,裂缝条数为4条,无量纲导流系数为12,不对称因子为0.4.

图4 水平井多段压裂非常规裂缝试井曲线
3.2 影响因素分析
不对称因子主要影响双线性流和过渡流阶段井底压力和压力导数曲线特征的变化,流体首先从地层流入压裂裂缝,再沿裂缝流入井筒,由于井筒两端裂缝不对称,裂缝短的一端首先结束双线性流阶段,因此,裂缝不对称因子越大,双线性流阶段结束的时间越早,即压力导数曲线斜率为0.25的直线结束越早;由于压裂裂缝为有限导流,裂缝越不对称,在双线性流阶段到过渡流阶段,井筒与裂缝之间的压差就越大,流体流过该区域时所消耗的压降就越大,所以,裂缝越不对称,双线性流阶段到早期线性流阶段井底压力和压力导数曲线幅度越高;当裂缝完全不对称时,流体首先沿裂缝做线性流后直接进入早期线性流阶段,因此,压力导数曲线的斜率不为0.25(图5)。

图5 不对称因子对井底压力和压力导数曲线的影响
压裂裂缝条数主要影响双线性流阶段到第二线性流阶段的井底压力和压力导数曲线特征的变化,在水平井长度不变的情况下,裂缝条数越多,裂缝与裂缝之间的间距就越小,裂缝条数的增加会提高水平井井筒附近地层的渗透率,水平井井筒压力越低,水平井井筒与裂缝之间的压差越大,对于定产生产的油井,原油流过该区域时所消耗的压降就越小,所以,双线性流阶段到第二线性流阶段井底压力和压力导数曲线幅度越低,系统径向流阶段压力导数曲线对裂缝条数并不敏感,说明系统径向流阶段主要反映的是压力波传播到距离水平井井筒比较远的区域的渗流特征(图6)。图6中无量纲井储系数为0.000 5,表皮系数为0.01,无量纲导流系数为12,不对称因子为0.4.
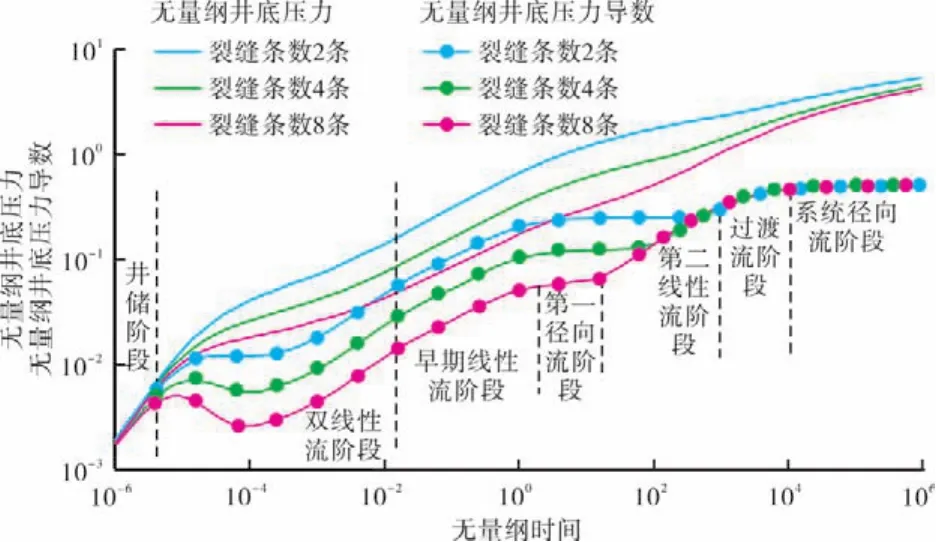
图6 裂缝条数对井底压力和压力导数曲线的影响
本文主要分析储集层被全部压裂开时,裂缝沿水平井不对称均匀分布对试井曲线的影响。从图7可以看出,在压裂裂缝条数不变的情况下,裂缝分布方式对试井特征曲线的影响主要集中在第二线性流阶段,压裂裂缝分布越不对称,即裂缝与裂缝之间的距离越小,第二线性流阶段持续的时间就越短,其压力导数曲线斜率不为0.50,系统径向流阶段开始的时间越早(图7)。图7中无量纲井储系数为0.000 5,表皮系数为0.01,裂缝条数为5条,无量纲导流系数为12,不对称因子为0.4.

图7 裂缝分布方式对井底压力和压力导数曲线的影响
裂缝导流系数越大,说明流体在裂缝中的流动阻力越小,裂缝导流系数对试井曲线的影响主要在双线性流阶段和早期线性流阶段。裂缝导流系数越大,井筒附近压差就越大,流体流过该区域时所消耗的压降就越小,沿裂缝方向流体流动阻力就越小,双线性流阶段结束时间越早(图8)。因此,裂缝导流系数越大,早期井底压力和压力导数曲线在井储阶段向双线性流阶段过渡曲线幅度越低;当裂缝导流系数为无穷大时,双线性流阶段消失,该阶段曲线特征为无限导流曲线特征。图8中无量纲井储系数为0.000 5,表皮系数为0.01,裂缝条数为5条,不对称因子为0.4.

图8 裂缝导流系数对井底压力和压力导数曲线的影响
4 实例应用
胜利油田樊154区块沙二段油藏多段压裂水平井M井,测试水平井井段为2 963~3 779 m,水平段长度为602 m,水平段井筒距离油层顶面为17.5 m,井筒半径为0.07 m,储集层有效厚度为35 m,平均孔隙度为12.4%,平均渗透率为2.27 mD,原油黏度为1.60 mPa·s,油藏压力为31.07 MPa,综合压缩系数为1.66×10-3MPa-1,原油体积系数为1.22.M井在3 185 m,3 550 m和3 760 m进行射孔压裂,其加砂量分别为25.1 m3,25.6 m3和 35.0 m3,压力恢复测试前油压为4.00 MPa,日产油量为16.5 t.根据M井实测井底压力与压力导数的双对数曲线形态,结合该油藏地质特征,选用有限导流水平井多段压裂非常规裂缝试井解释模型进行曲线拟合解释,由于该井没有进行微破裂影像监测,视人工压裂的3条裂缝均有效,并结合压裂施工设计与现场实际资料,解释裂缝拟合参数见表1.从图9可以看出,由(21)式和(22)式计算所得到的无量纲井底压力和压力导数数据与实测数据拟合效果很好,因此(21)式和(22)式可以用来解释多段压裂不对称试井资料。
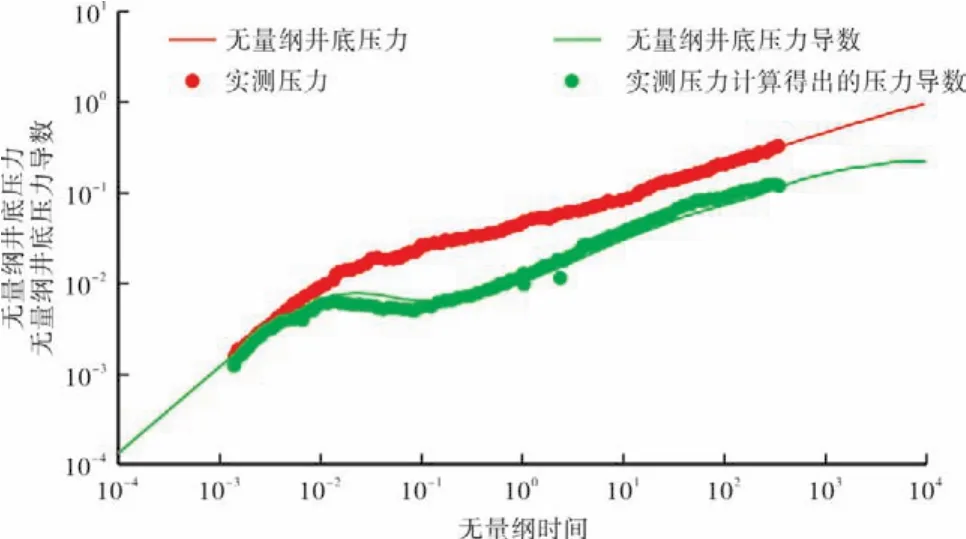
图9 (21)式和(22)式计算所得数据与实测数据拟合
定产生产时,首先将要绘制曲线的无量纲井筒储集系数、无量纲导流系数、裂缝条数、表皮系数和不对称因子代入(24)式中,计算Laplace空间下压力和时间数据,再通过Stehfest数值反演方法获得实空间无量纲压力曲线,然后结合实际的压降或压力恢复测试数据,绘制出实测压降或压力恢复测试数据曲线及其导数曲线,通过不断调整试井曲线的基本参数,使实测曲线与理论典型曲线达到最佳匹配,从而获得地层和裂缝的相关参数(表1)。

表1 M井裂缝拟合参数结果
5 结论
(1)利用点源函数基本理论,建立单条裂缝有限导流不对称裂缝试井解释模型,将本文的解析方法与Berumen数值差分方法进行了对比验证,本文给出的解析方法是可行的。
(2)利用叠加原理建立水平井多段压裂非常规裂缝试井解释模型,通过积分变换获得模型半解析解,利用Stehfest数值反演方法绘制井底压力和压力导数曲线。
(3)多段压裂非常规裂缝水平井与多段压裂常规裂缝水平井存在较大的差异。不对称因子越大,双线性流阶段结束的时间越早,当裂缝不对称因子为1时,不出现双线性流阶段;裂缝条数越多,系统径向流阶段的井底压力和压力导数曲线幅度越低;裂缝分布越不对称,第二线性流阶段压力导数曲线斜率为0.50的特征越不明显;裂缝导流系数越大,双线性流阶段压力导数曲线斜率为0.25的特征越不明显。
符号注释
A(i,j)——第 i条裂缝,第j个网格所对应的系数;
bf——裂缝宽度,m;
bfD——无量纲裂缝宽度;
C——井筒储集系数,m3/MPa;
CD——无量纲井筒储集系数;
CfD——无量纲导流系数;
Ct——综合压缩系数,MPa-1;
h——储集层厚度,m;
K——储集层渗透率,mD;
K0——零阶第二类Bessel函数;
Kf——裂缝渗透率,mD;
Lf——裂缝长度,m;
Lref——参考长度,本文取裂缝长度的一半,m;
M——裂缝条数,条;
N(xmD,α)——Green函数;
Ni——第i条裂缝网格数,个;
pa——任意位置地层压力,MPa;
paD——任意位置无量纲地层压力;
pˉaD——Laplace空间下任意位置无量纲地层压力;
pˉD——没有考虑井储及表皮效应的无量纲井底压力;
pf——裂缝压力,MPa;
pfD——无量纲裂缝压力;
pˉfD——Laplace空间下无量纲裂缝压力;
pˉfDavg——Laplace空间下无量纲裂缝平均压力;
pi——原始地层压力,MPa;
pˉwD——考虑井储及表皮效应的无量纲井底压力;
q——单位长度裂缝流量,m2/d;
qD——无量纲单位长度裂缝流量;
qˉD——Laplace空间下无量纲单位长度裂缝流量;
qˉD(i,j)——Laplace空间下第i条裂缝,第j个网格无量纲单位长度裂缝流量;
Q——井底产量,m3/d;
s——Laplace变量;
S——表皮系数;
t——生产时间,d;
tD——无量纲生产时间;
x,y——分别为直角坐标系x轴和y轴;
xasmy——井相对于裂缝不对称位置,m;
xD,yD——分别为无量纲直角坐标系x轴和y轴;
xw,yw——分别为井筒中心到直角坐标系原点x轴和y轴方向的位移,m;
xwD,ywD——分别为井筒中心到直角坐标系原点x轴和y轴方向的无量纲位移;
xD(i,j+1),xD(i,j)——分别为沿着 x轴方向第 i条裂缝第 j个网格起点和终点无量纲坐标;
xmD(i,j),ymD(i,j)——分别为沿着 x轴和 y轴方向第 i条裂缝第 j个网格中点无量纲坐标;
ywD(i,j)——第i条裂缝与井筒交点无量纲位置;
α——积分变量;
δ——Dirc函数;
θ——不对称因子;
μ——流体黏度,mPa·s;
ϕ——孔隙度,f;
ΔxDi——第i条裂缝网格无量纲步长。
[1] 何东博,贾爱林,冀光,等.苏里格大型致密砂岩气田开发井型井网技术[J].石油勘探与开发,2013,40(1):79-89.
HE Dongbo,JIA Ailin,JI Guang,et al.Well type and pattern optimi⁃zation technology for large scale tight sand gas,Sulige gas field[J].Petroleum Exploration and Development,2013,40(1):79-89.
[2] CINCO L H,SAMANIEGO V F,DOMINGUEZ A N.Transient pres⁃sure behavior for a well with a finite⁃conductivity vertical fracture[J].Society of Petroleum Engineers Journal,1978,18(4):253-264.
[3] CINCO L H,MENG H Z.Pressure transient analysis of wells with fi⁃nite conductivity vertical fractures in double porosity reservoirs[R].SPE 18172,1988.
[4] 陈汾君,汤勇,刘世铎,等.低渗致密气藏水平井分段压裂优化研究[J].特种油气藏,2012,19(6):85-89.
CHEN Fenjun,TANG Yong,LIU Shiduo,et al.Study on the optimi⁃zation of staged fracturing of a horizontal well in a tight gas reservoir with low permeability[J].Special Oil&Gas Reservoirs,2012,19(6):85-89.
[5] 谷建伟,于秀玲,田同辉,等.致密低渗透气藏压裂水平井产能计算与分析[J].特种油气藏,2016,23(2):77-82.
GU Jianwei,YU Xiuling,TIAN Tonghui,et al.Fractured horizontal well productivity forecast and analysis in low⁃permeability tight gas reservoir[J].Special Oil&Gas Reservoirs,2016,23(2):77-82.
[6] RILEY M F,BRIFHAM W E,HORNE R N.Analytic solutions for elliptical finite⁃conductivity fractures[R].SPE 22656,1991.
[7] TIAN D,LU J,NGUYEN H,et al.Evaluation of fracture asymmetry of finite conductivity fractured wells[J].Journal of Energy Resourc⁃es Technology,2010,132(1):11-17.
[8] BERUMEN S,TIABB D,RODRIGUEZA F.Constant rate solutions for a fractured well with an asymmetric fracture[J].Journal of Petro⁃leum Science and Engineering,2000,25(1):49-58.
[9] LUO W J.Preseeure transient analysis of multiwing fractures con⁃nected to a vertical wellbore[R].SPE 171556,2015.
[10] WANG L,WANG X.Type curves analysis for asymmetrically frac⁃tured wells[J].Journal of Energy Resources Technology,2014,136(2):1-8.
[11] 熊健,刘海上,赵长虹,等.低渗透气藏不对称垂直裂缝井产能预测[J].油气地质与采收率,2013,20(6):76-79.
XIONG Jian,LIU Haishang,ZHAO Changhong,et al.Study on pro⁃ductivity of asymmetrical vertical fracture well in low⁃permeability gas reservoirs[J].Petroleum Geology and Recovery Efficiency,2013,20(6):76-79.
[12] 曹宝军,李相方,姜子杰,等.压裂火山岩气井不对称裂缝产能模型研究[J].天然气工业,2009,29(8):79-81.
CAO Baojun,LI Xiangfang,JIANG Zijie,et al.A research on the asymmetric fracture productivity models for fracturing volcanic gas wells[J].Natural Gas Industry,2009,29(8):79-81.
[13] 王本成,贾永禄,李友全,等.多段压裂水平井试井模型求解新方法[J].石油学报,2013,34(6):1 151-1 158.
WANG Bencheng,JIA Yonglu,LI Youquan,et al.A new solution of well test model for multistage fractured horizontal wells[J].Acta Petrolei Sinica,2013,34(6):1 151-1 158.
[14] 李龙龙,姚军,李阳,等.分段多簇压裂水平井产能计算及其分布规律[J].石油勘探与开发,2014,41(4):457-462.
LI Longlong,YAO Jun,LI Yang,et al.Productivity calculation and distribution of staged multi⁃cluster fractured horizontal wells[J].Petroleum Exploration and Development,2014,41(4):457-462.
[15] OZKAN E,RAGHAVAN R.New solutions for well⁃test⁃analysis problems:part 1⁃analytical considerations[J].SPE Formation Eval⁃uation,1991,6(3):359-368.
[16] OZKAN E,RAGHAVAN R.New solutions for well⁃test⁃analysis problems:part 2 ⁃computional considerations[J].SPE Formation Evaluation,1991,6(3):369-378.
[17] GUO J J,WANG H T,ZHANG L H.Transient pressure and pro⁃duction dynamics of multi⁃stage fractured horizontal wells in shale gas reservoirs with stimulated reservoir volume[J].Journal of Atu⁃ral Gas Science and Engineering,2016,35(1):425-443.
[18] TIAN Q,LIU P H.Pressure transient analysis of non⁃planar asym⁃metric fractures connected to vertical wellbores in hydrocarbon res⁃ervoirs[J].Intenational Journal of Hydrogen Energy,2017,42(29):18 146-18 155.
[19] 包劲青,刘合,张广明,等.分段压裂裂缝扩展规律及其对导流能力的影响[J].石油勘探与开发,2014,41(2):281-289.
BAO Jinqing,LIU He,ZHANG Guangming,et al.Fracture propa⁃gation laws in staged hydraulic fracturing and their effects on frac⁃ture conductivities[J].Petroleum Exploration and Development,2014,41(2):281-289.
[20] 王晓冬,罗万静,侯晓春,等.矩形油藏多段压裂水平井不稳态压力分析[J].石油勘探与开发,2014,41(1):74-94.
WANG Xiaodong,LUO Wanjing,HOU Xiaochun,et al.Transient pressure analysis of multiple⁃fractured horizontal wells in boxed reservoirs[J].Petroleum Exploration and Development,2014,41(1):74-94.
[21] ZAKIAN V.Numercial inversion of Laplace transform[J].Elec⁃tronics Letters,1970,99(5):47-49
[22] 江涛,王玉根,张修明,等.在页岩气试井分析中Bessel函数溢出问题的解决方法[J].天然气工业,2017,37(6):42-45.
JIANG Tao,WANG Yugen,ZHANG Xiuming,et al.Solution to the numerical overflow of Bessel functions in the analysis of shale gas well testing[J].Natural Gas Industry,2017,37(6):42-45.
[23] 任龙,苏玉亮,郝永卯,等.基于改造模式的致密油藏体积压裂水平井动态分析[J].石油学报,2015,36(10):1 272-1 280.
REN Long,SU Yuliang,HAO Yongmao,et al.Dynamic analysis of SRV⁃fractured horizontal wells in tight oil reservoirs based on stim⁃ulated patterns[J].Acta Petrolei Sinica,2015,36(10):1 272-1 280.
[24] 吕志凯,冀光,位云生,等.致密气藏水平井产能图版及应用[J].特种油气藏,2014,21(6):105-110.
LV Zhikai,JI Guang,WEI Yunsheng,et al.Horizontal well produc⁃tion type⁃curve and its application in tight gas reservoirs[J].Spe⁃cial Oil&Gas Reservoirs,2014,21(6):105-110.

