环境因子对轻腌大黄鱼中溶藻弧菌生长/非生长界面的影响

郭全友，朱彦祺,2，姜朝军，李保国

0 引 言

大黄鱼（pseudosciaena crocea）是中国地方性海水鱼类，在中国渔业经济占据重要地位[1]。目前，轻腌加工已成为大黄鱼主要加工形式，加工后水产品食用方便、营养价值高，但由于其高蛋白、高含水率容易受到微生物污染，导致腐败变质和食品安全问题。

鲜大黄鱼室温下的特定腐败菌为弧菌和肠杆菌[2]，弧菌能黏附于大黄鱼的黏液，从而在储藏过程中导致大黄鱼的腐败。其中，溶藻弧菌（vibrio alginolyticus）为嗜盐嗜温性、兼性厌氧海生弧菌，广泛分布于世界各地海水及河口，数量居海水类弧菌之首[3]，适宜生长温度为17～35 ℃。Hilmer等[3]研究证明，溶藻弧菌为32 ℃储藏条件下鲯鳅的优势腐败菌，能促使大量组胺的形成；同时近年来研究证明溶藻弧菌是引起牙鲆和鳗鲡等许多经济鱼类发生细菌性鱼病的致病菌之一[4-5]，研究证实该菌与副溶血弧菌一样，易污染食物引起腹泻，能产生不耐热性肠毒素（heat-labile toxins，LT）和耐热性肠毒素（heat stable toxins，ST），是沿海地区食物中毒的常见的条件致病菌[6]。溶藻弧菌既能导致水产品的腐败又是一种致病菌，多见于海水及水产品中，抑制溶藻弧菌的生长对产品质量安全至关重要。

目前主要可通过“栅栏技术”改变微生物的生长环境，来达到抑制微生物的作用。栅栏技术[7]中，多使用水分活度、盐分、醋酸、Nisin、糖分等栅栏因子来控制微生物的生长。微生物的生长/非生长（growth/non- growth）界限可以通过数学模型来定义和描述，得到的数学模型可作为安全屏障参数，保证产品的安全性和稳定性[8]。目前微生物的生长/非生长界限模型的建模方法有 Logistic回归法[9]、最小多面体法[10]、人工神经网络模型[11]法、简化式法[11]等。Logistic回归是模拟食品中微生物生长边界（生长/非生长界面）常用的方法[12-16]，Fernandez-Navarro[17]与Dechuyffeleer[18]等都曾使用该模型建立微生物生长/非生长模型来控制微生物的生长。PNN人工神经网络模型是前馈型神经网络，具有强大的非线性模式分类能力，PNN神经网络结构简单、训练速度快，在模式分类问题中，它可以利用线性学习算法来实现非线性学习算法的功能，同时具有非线性算法的高精确度等性质，在解决生长/非生长界面问题时可以对其进行分类，Simon等[19]利用PNN神经网络模型对芽孢杆菌的生长情况进行了预测；Hajmeer等[20]使用PNN模型对细菌生长非生长数据进行建模分类。目前尚没有研究对溶藻弧菌的生长非生长模型进行研究，同时将logistic模型与人工神经网络模型对比能更好的对其生长界面进行预测。

本文主要研究了在25 ℃储藏条件下，水分活度、pH值及盐分的交互作用对轻腌大黄鱼货架期终点溶藻弧菌生长概率的影响，用Logistic回归和PNN人工神经网络建立该交互作用下的生长/非生长模型，比较3种影响因子对溶藻弧菌的生长抑制作用，及其生长动力学参数的变化。由此评估pH值、水分活度和盐分许用范围内水产品的稳定性，定义的非生长条件可作为抑制微生物、保障食品质量安全的指南，从而实现有效的保存方法，确保轻腌大黄鱼产品品质安全。

1 材料与方法

1.1 试验材料

菌株S1为从25 ℃轻腌大黄鱼货架期终点分离的菌株，菌株占比 58.1%，轻腌大黄鱼取自福建宁德某公司,盐分2.0%，含水率60.79±2.24%，水分活度（water activity，aw）0.96±0.002，菌株经16sRNA及MIDI气相鉴定后为溶藻弧菌（序列号：KY684259），4 ℃保存，S1每个月重新接种斜面保证活性。

1.2 试剂及仪器

胰蛋白胨大豆肉汤（tryptone soya broth，TSB）；胰蛋白大豆琼脂培养基（tryptose soya agar，TSA）；1%盐酸（NaCl）；1%氢氧化钠（NaOH）；甘油和氯化钠，国药集团化学试剂有限公司。

pHS-3C pH计，上海雷磁仪器厂; AW LAB-Touch PMB35水分活度仪，大昌华嘉商业(中国)有限公司; 微生物生长测定仪: 芬兰，Bioscreen公司; SW-CJ-1FB洁净工作台,上海博讯实业有限公司医疗设备厂; MIR-153低温培养箱，日本三洋公司; QT-2漩涡混合器，上海琪特分析仪器有限公司。

1.3 生长介质的制备

试验设计为多因子交互试验，使用TSB作为培养的介质。大部分弧菌类最大耐受aw为0.90～0.94，因此取aw为0.90、0.91、0.92、0.94、0.96共5个水平；一般鱼类的 pH值为 6.6～6.8之间，弧菌类最大耐受 pH值为4.8～5.0之间[21]，因此取 pH值为 4.5、5.0、5.5、6.0、6.5、7.0共6个水平；对市售轻腌大黄鱼盐分含量分析，86.8%的产品小于4.0%，考虑产品的特性，则设计在盐分1%、2%、3%、4%共4个水平下进行试验，共计120种情况，每种情况重复4次，参考文献[22]和[23]选取90例数据作为训练集，30例数据为验证集，其中其他条件不改变、当aw为0.91时作为验证集，aw为0.90、0.92、0.94、0.96均分数据为训练集，训练集与验证集情况如表 1所示。制备时添加甘油调节aw，利用稀盐酸和氢氧化钠调节pH值，用pH计确认最后读数。

表1 交互试验训练集与验证集设计Table 1 Design of training and validation set of interactive experiment

1.4 菌悬液的制备与接种

菌株活化：取溶藻弧菌接种于无菌营养肉汤中，震荡30 s，25 ℃培养24 h，划线得到单菌落。

菌悬液制备：用无菌介质环挑取菌株，接种到10 mL无菌TSB试管中，37 ℃培养12 h。取1 mL培养液至9 mL无菌生理盐水中得到10–1菌悬液，以此稀释，制成10–1、10–2、10–3、10–4、10–5、10–6梯度菌悬液，各取 0.1 mL 涂布于TSA平板，37 ℃培养48 h计数，选取菌量约105CFU/mL菌悬液作为接种液。

调节过pH值、水分、盐分的TSB溶液，经121 ℃灭菌处理，每孔180 μL接入200微孔板中，取105CFU/mL的接种液20 μL，确定最终接种液浓度为4.5×104CFU/ml，接种入孔，每个条件4组平行，1个空白，微生物生长测定仪BIOSCREEN中速震荡25 ℃培养，7 d内每隔1 h测其OD600nm值。

1.5 生长/非生长边界判别

当试验结束时，微孔中出现明显的沉淀物或混浊且OD 值读数高于空白3倍则判定为生长[24-26]。判定为生长的条件下，取微孔中培养液100 μL在营养琼脂平板上涂布，检验菌株是否仍为纯菌株。当OD值为1～3倍空白之间时，涂布TSA琼脂平板验证，若平板出现典型菌落，且菌数大于初始菌量0.5 lgCFU/mL时，则判定为生长[16]。每种情况下的生长概率由重复孔的生长情况计算得到。若4孔中的2孔判定为生长则该情况下的生长概率为50%。

1.6 生长／非生长模型构建

1.6.1 Logistic模型构建

选定90例数据为训练集用来建立模型。

简单Logistic方程为基于Logit-Boost算法与简单回归函数通过 5折交叉验证确定最优迭代次数的方法，数据在培训和测试中平均分配了5次，为最基础的Logistic模型。选用简单Logistic方程来拟合试验数据[9]

其中PO为生长/非生长概率，bi（i为0~3）为拟合参数，NaCl为盐分浓度（体积分数v/v）。

二阶线性 Logistic方程是一种建立在一个多项式的逻辑回归模型的算法，可避免对大系数的过度拟合[23]，使用二阶线性Logistic回归模型来拟合试验数据

式中PO为生长/非生长概率，bi（i为0~9）为拟合参数，NaCl为盐分浓度（体积分数v/v），若计算过程中该参数效果不显著则剔除。

1.6.2 PNN人工神经网络模型构建

概率神经网络是基于Bayes分类规则与Parzen窗的概率密度函数估计方法发展而来的一种并行算法[27]，PNN的结构由输入层、模式层、求和层、输出层组成[28-29]。

将试验数据归一化后，根据试验设计选取90例数据，盐分、pH值和aw作为三维向量进入输入层，进行训练，输出层神经元设定为1，结构概率≤0.5的记作非生长，大于0.5的记作生长。训练完成后，将验证集30例数据作为输入，验证训练模型的准确性。

1.7 模型拟合优度及预测力评价

1.7.1 拟合优度评价

Logistic模型拟合优度采用似然比测试（-2lnL，the likehood test）、赤池信息准则（AIC=-2lnL+2k，Akaike’s information criterion）、Hosmer–Lemeshow 测试（HL）和R2-Nagelkerke进行评价。-2lnL、AIC常用作对模型拟合优度的评判，数值越小，证明拟合的效果越好。Hosmer-Lemeshow常用来评估模型的拟合优度及任意数量的连续与分散的解释变量[30]，数值越小，拟合效果越好，但其无法将标准偏差纳入考虑，一个不理想的预测值也可能导致该值的升高，常结合R2-Nagelkerke值一起考虑，R2-Nagelkerke值主要反映了解释变量与响应变量间的关系，其值越接近1，拟合优度越好。

1.7.2 预测力评价

Logistic与 PNN神经网络模型的预测力采用C-matrix获得的正确率（fraction correct，FC）和假阳性率（false alarm rate，FAR）[29]，进行比较，FC值越接近于100%说明预测效果越好，FC值为预测值与实际值的吻合度，FAR为假阳性错判率，可作为模型的预测准确度的参考。

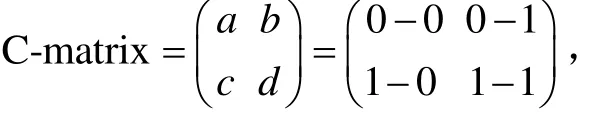
其中 FC=(a+d)/(a+b+c+d)，FAR=b/(a+b)。

1.8 模型验证

按试验设计选取30例数据为验证集用来验证模型，带入建立的Logistic模型与PNN模型中，通过FC和FAR验证模型的准确度和预测力。

1.9 生长动力学参数拟合

参考修艳辉等[31]针对环境因子对大黄鱼腐败希瓦氏菌生长影响的计数法，采用Gompertz方程对溶藻弧菌生长情况进行拟合，得到其生长动力学参数。

式中y为OD值；x为时间，h；a1为最小OD值；b1为最大 OD值与最小 OD值之差；c1为比生长速率，h–1；d1为延滞期，h。

1.1 0 数据分析

模型拟合通过软件Spss 18.0，通过Origin9.0绘制生长/非生长曲线（选取概率PO＝0.1、0.5、0.9时的预测值）。

人工神经网络建立通过MatlabR2016b建模。

2 结果与分析

2.1 生长/非生长模型构建及评价

2.1.1 Logistic回归模型拟合

溶藻弧菌3种生长/非生长模型的拟合参数如表2所示。表2可见，采用简单Logistic方程，盐分、aw与pH对溶藻弧菌生长影响极显著（显著性 P<0.01），采用二阶线性Logistic方程，aw、pH值、盐分与pH值交互作用、pH值与aw交互作用对溶藻弧菌生长影响极显著（显著性P<0.01），分别拟合得到式（4）与式（5）。

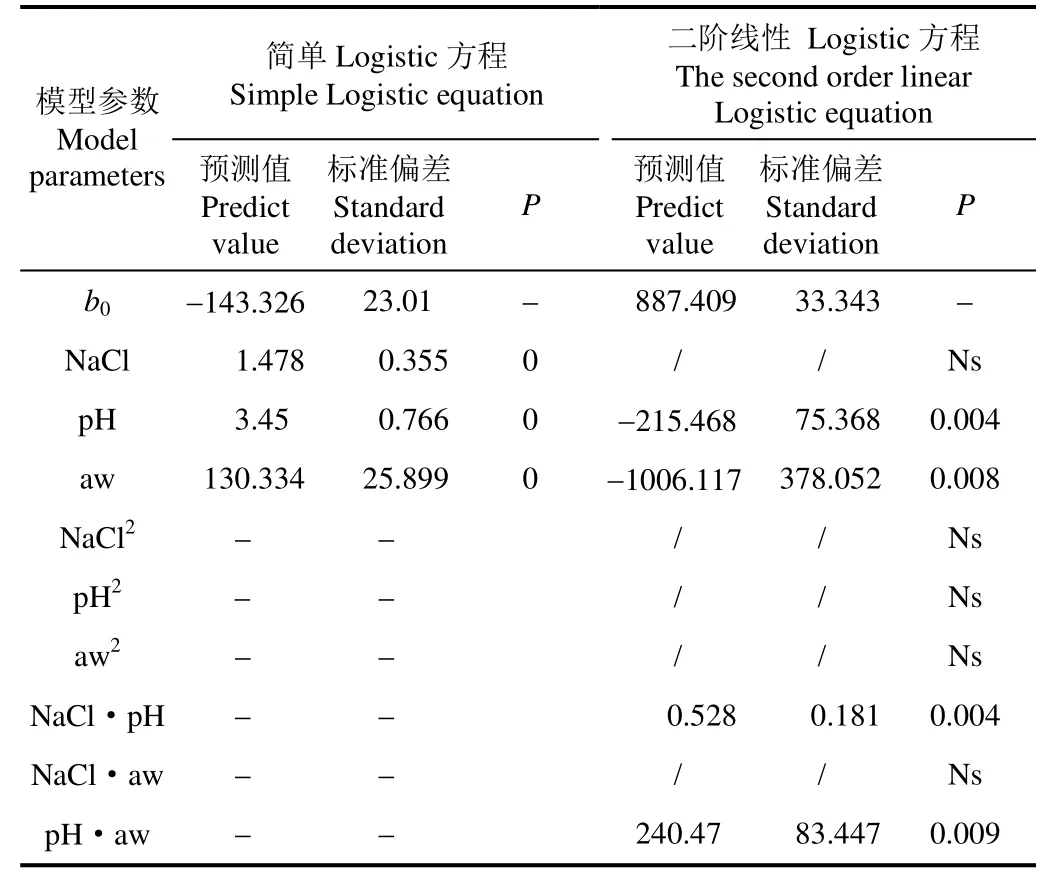
表2 Logistic模型拟合参数及拟合优度比较Table 2 Comparison of Logistic model fitting parameters and goodness of fit

2.1.2 PNN模型的建模结果

建立隐含层数2，输出层神经元1的PNN模型。网络建立后，开始训练网络，网络训练最优速度为0.1 s，训练集正确率为95.6%，按照试验设计选取30例数据进行验证。PNN 网络的测试诊断结果显示 30例验证中有27例数据符合实际试验情况分类，准确率为90.0%。

2.1.3 3种模型拟合优度评价与验证

模型拟合优度参数如表3所示，正确率（FC）通常表示模型的预测能力[29]，简单Logistic方程训练集、验证集的FC分别为87.5%与83.3%，二阶线性Logistic方程训练集、验证集的 FC为 94.80%与 90.90%，优于简单logistic方程。同时二阶线性Logistic方程的R2-Nagelkerke为0.91，Hosmer-Lemeshow为x2=0.55（P=1.00），假阳性率与假阴性率均优于简单Logistic方程。陈琛等[22]利用二阶线性logistic方程建立了环境因子交互作用下蜡样芽孢杆菌生长/非生长模型，结果显示logistic回归模型拟合度较高，具有较广的适用范围。渠飞翔等[24]利用二阶线性 logistic方程建立了软烤贻贝中蜡样芽孢杆菌生长/非生长界面的模型，结果显示该模型在预测软烤贻贝中蜡样芽孢杆菌的生长/非生长情况有很高的精确度和很好的适用性。

对于 PNN神经网络模型来说其训练集 FC高达95.6%，验证集FC为90.0%，但训练集和验证集的假阳性率却较 Logistic模型要高。PNN人工神经网络模型能够短时间内进行生长/非生长数据的快速分类，且总体准确率较高，但仅仅能对生长非生长数据进行分类，无法准确给出生长/非生长的界面，无法给出具体细致的生长概率，但其快速的分类功能却能为工业生产提供便利。3种模型拟合优度结果显示，二阶线性Logistic方程更能有效预测溶藻弧菌生长/非生长概率，能用于环境因子交互作用下溶藻弧菌生长/非生长概率变化趋势。

表3 三种模型拟合优度评价和比较Table 3 Evaluation and comparison of goodness fitting of three models

2.2 环境因子对溶藻弧菌生长概率的影响

2.2.1 盐分对溶藻弧菌生长/非生长的作用

图1为NaCl对溶藻弧菌生长概率影响的示意图，根据模型拟合出生长概率 PO=0.1、0.5、0.9的生长概率分界线，在PO=0.9界限之上则代表该种对应条件下生长概率大于0.9，该条件适宜生长；在PO=0.1以下则说明该区域下盐分、pH值及水分活度的交互作用对溶藻弧菌有较好的抑制作用，溶藻弧菌的生长概率小于 0.1。随着盐分的增大，生长非生长的界限明显向低水分活度，低pH值方向移动，水分活度和pH值的交互作用逐渐减弱；PO=0.1到PO=0.9之间的距离也逐渐增大，生长/非生长的转变区域逐渐增大，溶藻弧菌在盐分4.0%时生长最为活跃。

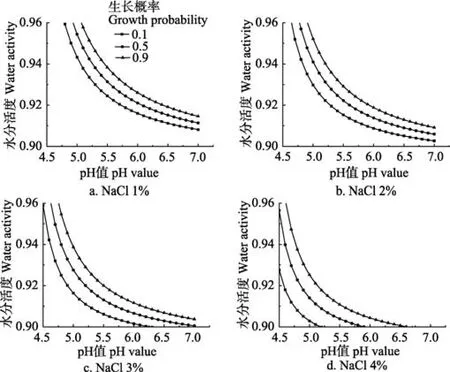
图1 对溶藻弧菌生长概率的影响Fig.1 Influence of the growth probability of Vibrio alginolyticus by NaCl

图2 中为1.0%～4.0% NaCl和不同aw条件下，生长概率随pH值增大的变化情况。盐分1.0%、aw为0.96时，生长概率在pH值为4.6时开始增大，随pH的增大生长概率逐渐增大最终达到1；aw为0.94条件下，生长概率在pH值为4.8时开始增大；aw为0.92、0.91条件下生长概率分别在pH值为5.3、5.9时开始增大，最终到达1和0.28；盐分1.0%、aw为0.90时，无论pH值如何变化，该交互作用下溶藻弧菌均不生长。

图2 盐分（NaCl）、水分活度和pH值交互作用下溶藻弧菌的生长概率Fig.2 Growth probability of Vibrio alginolyticus under interaction effects of salt (NaCl)、aw and pH uallue

盐分2.0%时，aw为0.96、0.94、0.92条件下，生长概率在pH值为4.5时均为0，随pH值的增大生长概率逐渐增大最终达到1；aw为0.91条件下，生长概率在pH值为4.7时开始增大，在pH值为7时达到0.94；盐分2.0%、aw为0.90时，无论pH值如何变化，该交互作用下溶藻弧菌均不生长。

盐分3.0%、4.0%时，aw为0.91条件下，生长概率在分别在pH值为4.7、4.5时开始增大最终到达1，与盐分1.0%、2.0%不同，当盐分为3.0%、4.0%时，aw为0.90条件下生长概率在pH值为5.1、4.6时开始增大，最终到达0.42和1。盐分越高，pH与aw的交互作用就被减弱，溶藻弧菌越适宜生长，生长界限开始变化的点趋于低pH值范围。但是，通常高盐分对腐败菌有生长抑制作用[31]，其机理在于高 Na+造成的高渗条件会导致细胞质失水从而引起质壁分离，进而膨压下降，细胞生长变慢而停止，生长受到抑制甚至死亡。修艳辉等[31]对单因素条件下环境因子对腐败希瓦氏菌的生长非生长界面做了研究，结果显示在25 ℃时，腐败菌的生长概率随盐分的增加而逐渐降低，当盐分大于等于 12%时腐败希瓦氏菌完全不生长。造成差异的主要原因在于菌类自身的特性有所不同，溶藻弧菌分离于 25 ℃轻腌大黄鱼货架期终点，为嗜盐菌，对盐分有较强的耐受性[3]，故在 4.0%盐分条件下，可减弱pH值与aw的交互作用，减少生长抑制。

2.2.2 aw对溶藻弧菌生长/非生长的作用

aw为0.92、0.94、0.96时，溶藻弧菌的生长概率受盐分影响逐渐减小，随pH值的增大而增大。aw越高，pH值与盐分的交互作用就被减弱，溶藻弧菌越适宜生长。Deschuyffeleer[18]研究了pH值、aw及酒精含量对高糖烘焙类食品中腐败菌的生长抑制作用，结果显示随着aw从0.89下降到0.755，目标腐败菌的生长受到抑制，生长概率逐渐降低。对于溶藻弧菌，当aw低于0.91时，盐分与pH值的交互作用逐渐受到影响，溶藻弧菌的生长同样也随水分活度的下降受到抑制。

2.2.3 pH值对溶藻弧菌生长/非生长的作用

pH值为4.5时，溶藻弧菌的生长受到强烈抑制，pH值为5.0~6.5时，溶藻弧菌的生长概率发生明显增长，aw为0.96、0.94、0.92条件下，生长概率在盐分4%时均能上升到1，概率变化的起始点也趋向低盐分梯度，aw为0.90条件下的生长概率也随盐分增大而增大最终到达0.86。Dang[7]研究了乙酸、aw、pH值对结合酵母生长非生长的交互作用，结果显示，随着pH值的降低，结合酵母的生长概率也随之降低，生长界限向更低乙酸、更高aw方向偏移，证明了低pH值是影响结合酵母生长的主要因素，在低pH值范围内pH值的改变只能引起生长概率微小的改变，高pH值范围内pH值的改变可以引起生长概率巨大的变化，该结论与本文结果相同。

2.3 环境因子对溶藻弧菌生长动力学参数的影响

图3为盐分1.0%～4.0%条件下，交互作用对溶藻弧菌生长动力学参数的影响。如图3a、图3b所示，在盐分1%时，比生长速率在aw为0.96且pH值为7时最大，为0.144± 0.006 h-1，且随pH值的下降而减小，生长速率明显减缓，同时该条件下的延滞期最小为 2.84±0.41 h；aw为0.94时，pH值为6时比生长速率为0.115±0.068 h-1，延滞期为10.56±0.37 h，延滞期随pH值的减小而增大；aw为0.92时，比生长速率很小，pH值4.5～7范围内的延滞期均大于30 h，生长迟缓，生长受到抑制。

图3c、图3d所示，在盐分2.0%时，比生长速率在aw为0.96且pH值为7时最大，为0.099±0.003 h-1，小于盐分1.0%时的比生长速率，但该条件下的延滞期比盐分1.0%时的小，为1.27±0.21 h；aw为0.92时，比生长速率总体上随pH的增大而增大，从0.027增长到0.072 h-1，大于盐分1.0%的情况。

图3e、图3f所示，在盐分3.0%时，aw为0.92时，比生长速率经显著性分析明显大于盐分 1.0%，2%的情况，延滞期有明显缩短，从1%时33 h左右缩短到15 h左右；aw为0.91时，溶藻弧菌也有缓慢生长。

图3g、图3h所示，在盐分4.0%、aw为0.90时，溶藻弧菌有缓慢生长，比生长速率为 0.02～0.03左右，延滞期在17.3～43.5 h范围内随pH值的减小而增大。有学者[32]研究了腐败菌随温度变化其生长动力学参数的变化，结果大多显示比生长速率随着温度的升高而增大，温度与延滞期及比生长速率均存在线性关系，但很少有学者深入探究腐败菌生长动力学参数随其他环境因子而变化的规律。

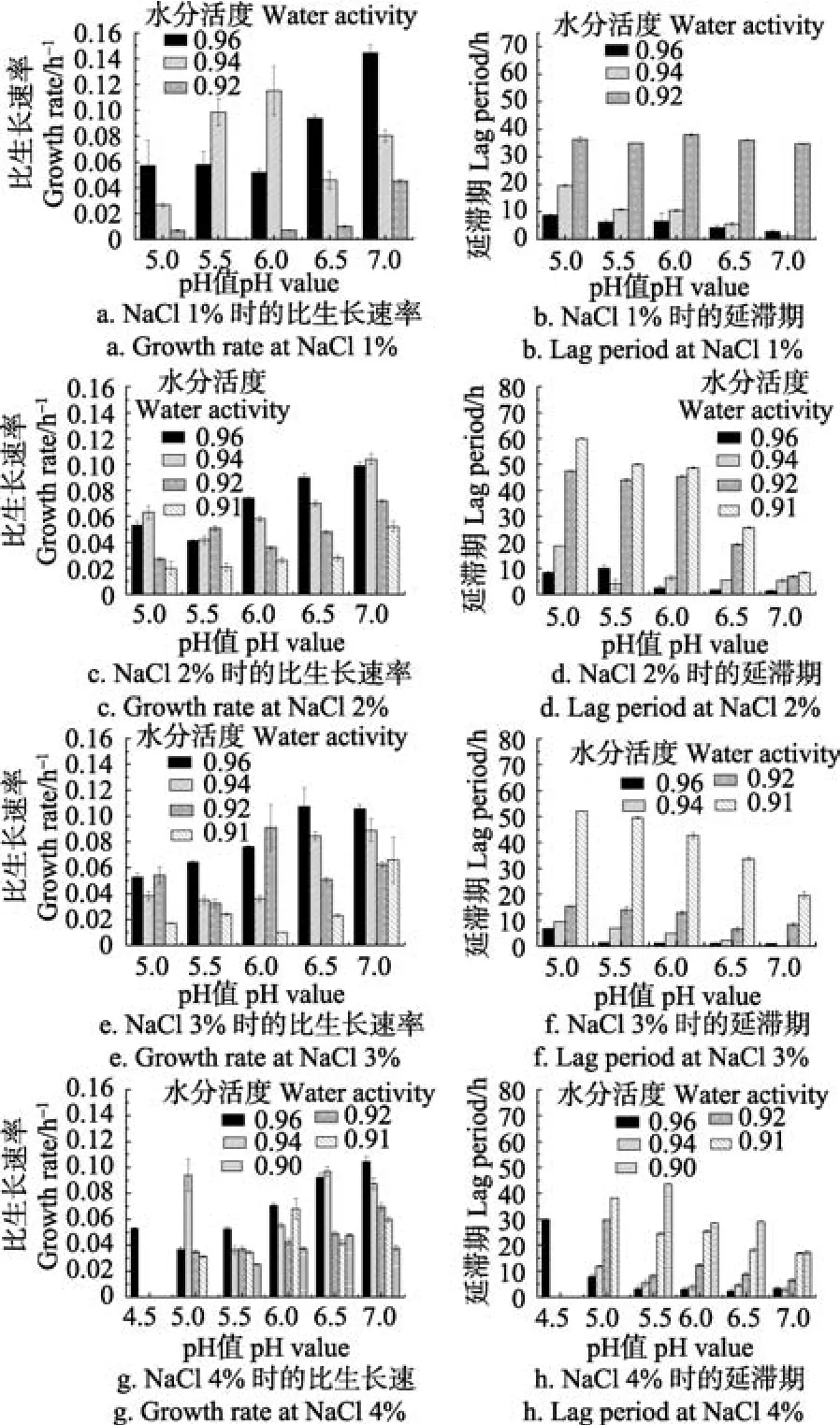
图3 环境因子对溶藻弧菌生长动力学参数的影响Fig.3 Effects of environment factors on growth kinetics parameters of Vibrio alginolyticus

3 结 论

本文研究了环境因子对源自轻腌大黄鱼的溶藻弧菌生长/生长界面和生长动力的影响。通过建立Logistic 生长/非生长模型，可以评估pH值、aw和盐分许用范围内的水产品稳定性，同时PNN模型虽不能具体预测溶藻弧菌的生长概率大小，但可对生长和非生长进行分类，由于其预测分类速度很快，可以在工业生产中起到重要作用。同时，通过概率模型预测的非生长区域可为保障水产品质量安全而不使用化学防腐剂提供指导。另外，预测模型可作为相关抑菌因素影响的有用指标，进而实现有效的保存方法，确保轻腌大黄鱼产品的稳定性和安全。主要结论如下：

1）建立了溶藻弧菌简单 logistic模型、二阶线性Logistic模型和PNN人工神经网络模型，来预测溶藻弧菌的生长/非生长情况。二阶线性logistic模型和PNN人工神经网络模型的训练集正确率分别为94.8%和95.6%，验证集正确率为90.9%和90.0%。PNN人工神经网络的能对生长、非生长数据进行快速分类，但二阶线性 logistic模型能更好的反映溶藻弧菌的生长概率预测。

2）随着盐分的升高，生长非生长的界限明显向低aw、低pH值方向移动，PO＝0.1到PO＝0.9之间的距离也逐渐增大，生长非生长的转变区域逐渐增大。溶藻弧菌为轻腌大黄鱼中分离嗜盐菌，对盐分有较强的耐受性，在4.0%盐分条件下，可减弱pH值与水分活度的交互作用，生长较为活跃。

3）在相同盐分条件下，高aw且pH值较高时比生长速率较高，溶藻弧菌生长繁殖迅速，延滞期也相应缩短；随着盐分的升高，0.91与0.90低aw条件下溶藻弧菌也开始缓慢增长，但存在较长时间的延滞期。高盐分下的交互作用使溶藻弧菌比生长速率增大，延滞期减小，对溶藻弧菌的生长有促进作用。

[1] 许钟，郭全友. 淡腌大黄鱼贮藏中的品质变化及腐败菌分析[J]. 食品科学，2008，29(12)：697－700.Xu Zhong，Guo Quan-you, Quality changes and spoilage bacteria in light salted pseudosciaena crocea during Storage[J], Food science, 2008, 29(12): 697－700. (in Chinese with English abstract)

[2] 郭全友，王锡昌，杨宪时. 不同贮藏温度下养殖大黄鱼货架期预测模型的构建[J]. 农业工程学报，2012，28(10)：267－273.Guo Quanyou, Wang Xichang, Yang Xianshi. Predictive model construction of shelf life for cultured Pseudosciaena crocea stored at different temperatures[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(10): 267－273. (in Chinese with English abstract)

[3] Hilmer A F, John D B, Malin C, et al. Identification and decarboxylase activities of bacteria isolated from decomposed mahimahi (Coryphaena hippurus) after incubation at 0 and 32C[J]. International Journal of Food Microbiology, 1985, (6): 331－340.

[4] 程亚琪，隋凌云. 一起溶藻弧菌引起的食物中毒[J]. 临床医药文献电子杂志，2014，1(11)：2043 Chen Yaqi, Sui Lingyun, With food poisoning caused by Vibrio alginolyticus[J], Electronic Journal of Medicine clinical literature, 2014, 1(11): 2043. (in Chinese with English abstract)

[5] Hormansdorfer S, Wentges H, Neugebaur K, et al. Isolation of Vibrio alginolyticus from seawater aquaria[J].International Journal of Hygiene and Environmental Health,2000, 203(2): 169－175.

[6] KanekoT,Colwell R..Distribution of Vibrio parahaemolyticus and Related Organisms in the Atlantic Ocean off South Carolina and Georgia[J].Applied and Environmental Microbiology.1974, 28(6)：1009-1017.

[7] Dang T D T, Mertens L, Vermeulen A, et al. Modelling the growth/no growth boundary of Zygosaccharomyces bailii in acidic conditions: A contribution to the alternative method to preserve foods without using chemical preservatives[J].International Journal of Food Microbiology, 2010, 137(1): 1－12.

[8] Garcia D, Ramos A J, Sanchis V, et al. Predicting mycotoxins in foods: a review. [J]. Food Microbiolgy, 2009,26(8):757－769.

[9] Sosa-Morales M E, Garcia H S, López-Malo A.Colletotrichum gloeosporioides growth-no growth interface after selected microwave treatments[J].food Protection , 2009, 72(7): 1427－1433.

[10] Theys T E, Geeraerd A H, Devlieghere F, et al. On the selection of relevant environmental factors to predict microbial dynamics in solidified media[J]. Food Microbiology, 2010, 27 (2): 220－228.

[11] Bolton L F，Frank J F. Defining the growth/no-growth interface for Listeria monocytogenes in Mexican-style cheese based on salt, pH, and moisture content[J]. Journal of Food Protection, 1999, 62 (6): 601－609.

[12] Koutsoumanis P K, Sofos N J. Effect of inoculum size on the combined temperature, pH and aw limits for growth of Listeria monocytogenes[J]. International Journal of Food Microbiology, 2006, 104 (1): 83－91.

[13] Skandamis P N, Stopforth J D, Kendall P A. Modelling the effect of inoculum size and acid adaptation on growth/no growth interface of Escherichia coli O157: H7 [J].International Journal of Food Microbiology, 2007, (3),237-249.

[14] Marín S, Hodzic I, Ramos A J, et al. Predicting the growth/no growth boundary and ochratoxin A production by Aspergillus carbonarius in pistachio nuts[J]. Food Microbiology. 2008,25(5), 683－689.

[15] Presser K A, Ross T，Ratkowsky D A. Modelling the growth limits (growth no growth interface) of Escherichia coli as a function of temperature, pH, lactic acid concentration, and water activity[J]. Applied and Environmental Microbiology,1998, 64(5): 1773－1779.

[16] Lanciotti R, Sinigaglia M, Gardini F, et al. Growth/no growth interfaces of Bacillus cereus, Staphylococcus aureus and Salmonella enteritidis in model systems based on water activity, pH, temperature and ethanol concentration[J]. Food Microbiology, 2001, 18(6): 659－668.

[17] Fernandez-Navarro F, Valero A, Hervas-Martinez C.Development of a multi-classification neural network model to determine the microbial growth/no growth interface[J].International Journal of Food Microbiology, 2010, 141(3)：203－212.

[18] Deschuyffeleer N, Vermeulen A, Daelman J. Modelling of the growth/no growth interface of Wallemia sebi and Eurotium herbariorum as a function of pH, aw and ethanol concentration[J]. International Journal of Food Microbiology,2015(192)：77－85.

[19] Simon L, Karim M N. Probabilistic neural networks using Bayesian decision strategies and a modified Gompertz model for growth phase classification in the batch culture of Bacillus subtilis[J]. Biochemistry Engineer, 2001, 7(1):41－48.

[20] Hajmeer M, Basheer I. A probabilistic neural network approach for modeling and classification of bacterial growth/no-growth data[J]. Journal of Microbiological Methods,2002, 51 (2): 217－226.

[21] Parthena Kotzekidou, Chapter 3 - Factors influencing microbial safety of ready-to-eat foods, In Food Hygiene and Toxicology in Ready-to-Eat Foods[M] San Diego, Academic Press, 2016：33－50.

[22] 陈琛，李学英，杨宪时，等. 环境因子交互作用下蜡样芽孢杆菌生长/非生长界面模型的建立与评价[J]. 现代食品科技，2015，31(12)：205-213.Chen Chen, Li Xueying，Yang Xiangshi, et al. Modeling and Evaluating the Growth/No Growth Boundaries of Bacillus cereus: Effect of Temperature, pH, and Water Activity[J].Modern Food Science and Technology, 2015, 31(12): 205－213. (in Chinese with English abstract)

[23] Ce Yu, Valerie J. Davidson, Simon X. Yang. A neural network approach to predict survival/death and growth/no-growth interfaces for Escherichia coli O157: H7[J] Food Microbiology, 2006(23): 552–560.

[24] 渠飞翔，李学英，杨宪时. 软烤贻贝中蜡样芽孢杆菌生长/非生长界面模型建立与评价[J]. 食品与机械，2016，32(4)：143－147.Qu Feixiang, Li Xueying，Yang Xianshi. Modeling and evaluating on growth/no growth boundaries of Bacilus cereus on soft-baked musels[J]. Food & Machinery, 2016, 32 (4):144－147. (in Chinese with English abstract)

[25] 赵学广，李学英，杨宪时. 三因子金黄色葡萄球菌生长/非生长模型构建[J]. 食品与机械，2016，32(3)：122－126.Zhao Xueguang, Li Xueying, Yang Xianshi. Establishment of Model on growth/no growth boundary of Staphylococcus aureus based for three factors[J]. Food & Machinery, 2016,32(3): 123－126. (in Chinese with English abstract)

[26] Marvig C L, Kristiansen R M, Nielsen D S. Growth/no growth models for Zygosaccharomyces rouxii associated with acidic, sweet intermediate moisture food products[J].International Journal of Food Microbiology, 2015,192(2): 51－57.

[27] 孙俊，路心资，张晓东，等. 基于高光谱图像的红豆品种GA-PNN神经网络鉴别[J]. 农业机械学报，2016，47(6)：215－221.Sun Jun, Lu Xinzi, Zhang Xiaodong, et al. Identification of Red Bean Variety with Probabilistic GA-PNN Based on Hyperspectral Imaging[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47 (6): 215－221.

[28] 赵桂艳，李一峰. 基于PNN神经网络和聚类分析的变压器故障诊断[J]. 信息系统工程，2015，28(6)：94－95.Zhao Guiyan, Li Yifeng. PNN transformer fault diagnosis based on neural network and cluster analysis[J]. Information Systems Engineering, 2015, 28(6): 94－95.

[29] Hajmeer M N, Basheer I A. A hybrid Bayesian–neural network approach for probabilistic modeling of bacterial growth/no-growth interface[J]. International Journal of Food Microbiology, 2003, 82(3), 233–243.

[30] Valero A, Carrasco E, Perez-Rodriguez F, et al. Growth/no growth model of Listeria monocytogenes as a function of temperature, pH, citric acid and ascorbic acid[J]. European Food Research and Technology, 2006, 224(1): 91－100.

[31] 修艳辉，郭全友，姜朝军. pH、水分活度和NaCl对腐败希瓦氏菌生长/非生长界限及生长动力学参数的影响[J].现代食品科技，2016，32(6): 156－162+199.Xiu Yanhui, Guo Quanyou，Jiang Chaojun. Effect of pH,water activity and common salt on the growth/no growth boundary and growth kinetic parameters of Shewanella putrefaciens[J]. Modern Food Science and Technology, 2016,32(6): 156－162. (in Chinese with English abstract)

[32] 朱彦祺，郭全友，李保国，等. 不同温度下腐败希瓦氏菌(Shewanela putrefaciens)生长动力学模型的比较与评价[J].食品科学，2016，37(13): 147－152.Zhu Yanqi, Guo Quanyou, Li Baoguo, et al. Comparison and evaluation of models for the growth of Shewanella putrefaciens at different temperatures[J]. Food Science, 2016,37(13): 147－152. (in Chinese with English abstract)