直线驱动型并联机器人工作空间分析与优化

吴超宇 钱小吾 余 伟 于 今

(1.重庆大学机械传动国家重点实验室, 重庆 400044； 2.镇江高等专科学校基础部， 镇江 212002)

0 引言

根据并联机器人的结构和关节驱动方式，可以将其分为直线驱动型和旋转驱动型2种[1]。EPFL的最新研究[2]对直线型并联机器人和旋转型并联机器人的运动特点与机构性能进行了对比分析，旋转型具有更优良的动态特性，而直线型则具有更大的工作空间，较适应于并联机床等应用。研究直线驱动并联机器人工作空间的方法主要有解析法、几何法和数值法，在解析法方面，JO[3]提出，后经GOSSELIN[4]发展的圆弧相交几何法,将工作空间边界构造归结为12张球面片求交问题。MERLET[5]研究了固定平台参考点求解相应极限姿态空间的解析方法，解析法精确，但是计算量大，较复杂，不具有通用性。几何法作图简单，但是非常复杂，难以表达机器人的运动，针对直线驱动并联机器人无法有效得到参数对工作空间的影响趋势。在数值法研究方面，通常采用数值搜索、牛顿迭代等方法，同时考虑到各关节转角的约束、各杆长的约束和机构各构件的干涉来确定并联机器人的工作空间，且采用数值积分的方法计算工作空间的体积，比较接近实际[6-10]。文献[11-13]提出了一种计算6自由度并联机器人的定向工作空间的离散化方法。这些方法存在边界计算不精确，计算量大等问题。在并联机器人工作空间优化方面，所查阅的文献中基本上是以工作空间体积最大为优化设计目标，获取更优良的运动学性能，但是由于旋转型并联机器人的整机布局比较紧凑，而直线型并联机器人的整机布局比较松散，直线型与旋转型相比，整机结构尺寸比较大，这样会导致直线型并联机器人制造成本、占用空间和功率消耗的增加。因此，以工作空间体积最大为优化目标对直线驱动型并联机器人研究是不合理的。

本文提出一种极坐标变步长迭代搜索法求解出并联机器人的工作空间，并研究机器人各结构参数对工作空间形状、大小的影响趋势，为下一步工作空间优化中设计变量的范围确定提供了依据。提出一种综合机构灵巧度与工作空间利用率的全局混合性能指标，针对不同的作业要求，得到兼顾机器人灵巧度与空间利用率的机械结构参数，通过对不同权重下优化得到的参数进行仿真实验，验证目标函数的正确性和有效性。通过激光跟踪仪测出的实际工作空间与理论工作空间模型进行对比，验证工作空间理论模型的正确性，为后续的尺度综合研究提供依据。

1 运动学模型

本文研究的直线驱动型并联机器人如图1所示，由静平台、动平台、同步带电缸、滑块、U型虎克铰、3组平行四边形支链杆件等组成，每组支链分别通过2个虎克铰(U副)连接动平台与滑块，滑块通过平移副(P副)由同步带电缸驱动。3组电缸的投影是120°，均匀分布，与水平面呈一个固定的角度，下端交于一点。3个电动机安装在同步带电缸的上方，直线驱动3个滑块，杆件连接处采用一种特殊设计的U型虎克铰结构，该结构能够保证平行四边形两组杆件的同向性，并能扩大关节的转动能力。

图1 直线驱动型并联机器人三维模型Fig.1 Three dimensional model of linear driven parallel robot1.静平台 2.交流伺服电机 3.同步带电缸 4.滑块 5.U型虎克铰 6.平行四边形支链 7.动平台

图2是直线驱动型并联机器人的原理图，图3是单个支链的原理图，设定笛卡儿直角坐标O{x,y,z}在静平台△A1A2A3的中心O点处并且在动平台△B1B2B3的中心P处建立一个移动的动笛卡儿坐标P{x′,y′,z′}，由于动平台与静平台平行，并且这个并联机构只有3个平移自由度，所以x轴与x′轴平行，并且x轴沿着lOA1方向，向量lOA1平行于lPB1，z轴均朝上，3条运动直线DiEi相交于M点，并且与静平台相交于Ai(i=1,2,3),并且静平台半径为a。3个长度为l的杆与动平台相交于Bi,半径为b,P关节的滑块在限定的Di与Ei之间移动，α是静平台与DiEi导轨的夹角。角度φi是x轴与静平台向量lOAi的夹角，因为静平台与动平台平行，所以夹角也适用于动平台。为了简化方程，定义

φi=(i-1)×120°

(1)

其中i=1，2，3。在图3中，Di为同步带轮的中心点，Ci是经过同步带轮中心Di沿电缸轴向直线与过滑块与连杆的虎克铰中心Fi的垂直电缸导轨直线的交点，Fi是滑块与连杆的连接虎克铰的中心，Bi是连杆与动平台的虎克铰的中心，P是动平台的几何中心，Ei是选定的驱动轴的原点，滑块到同步带轮中心Di的距离是di(i=1,2,3)。Hi为滑块高度，也就是虎克铰到滑块的距离。

图2 直线驱动型并联机器人原理图Fig.2 Schematic of linear driven parallel robot

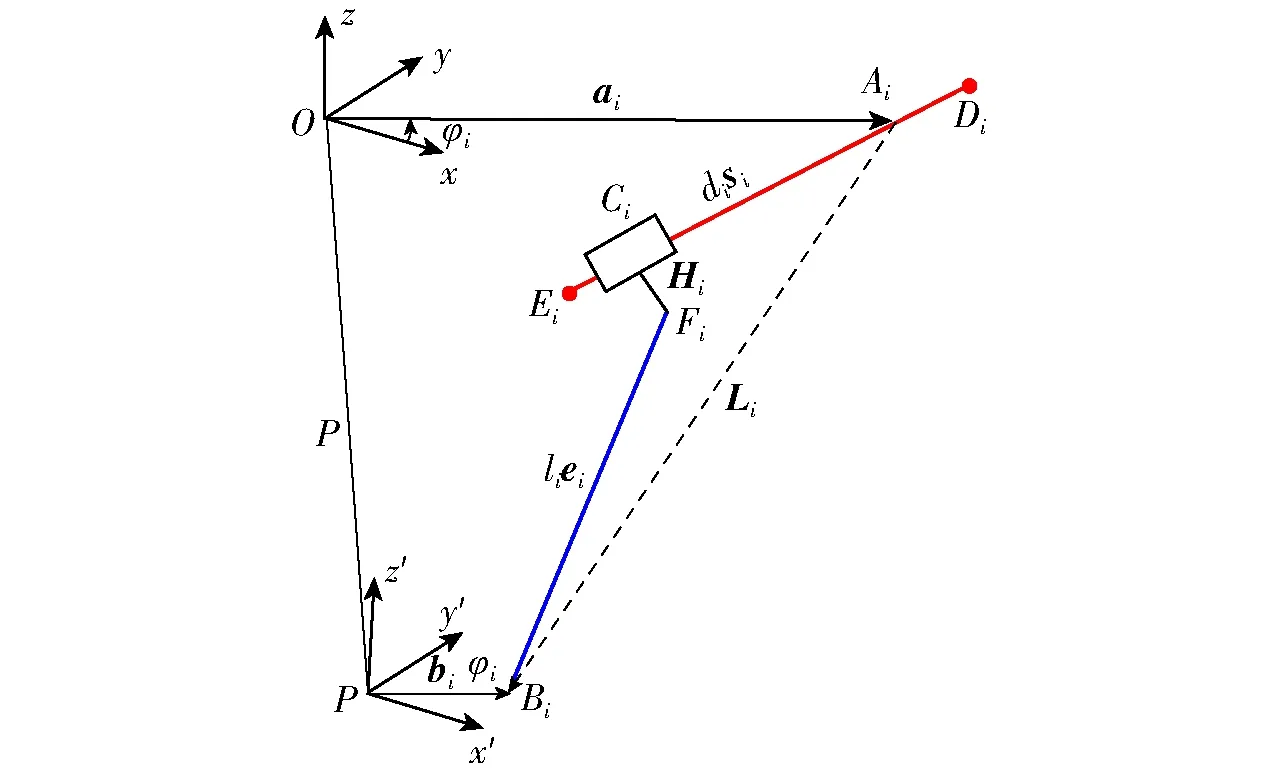
图3 单支链原理图Fig.3 Schematic of one typical kinematic chain

如图3所示，点Ai与Bi关于O与P的位置向量可以被写成

(2)

(3)

左上标向量表示在哪个坐标系中被表达。为了简洁表述，当在静平台的坐标系中被表述时，左上标可以省略。例如Oai=ai，动平台相对于静平台的位置与方向可以由一个方向向量，P=lOP，和一个3×3的旋转矩阵ORP组成，由于动平台只有3个平移运动，所以旋转矩阵ORP也就是一个单位矩阵，所以Pbi=bi，如图3所示，每一个支链的闭环回路方程可以写成[14]

lei=Li-disi-Hi

(4)

其中

Li=P+bi-ai

(5)

(6)

(7)

式中ei——lFiBi的单位向量di——第i个滑块的线性位移si——DiEi的单位向量Hi——滑块高度，它的模长可以表示为|h|是个定值

将式(4)左右两边分别点乘本身，可以得

l2=(Li-disi-Hi)(Li-disi-Hi)T

(8)

化简可以得到

(9)

其中si与Hi是垂直的2个向量，所以si与Hi的乘积是0。式(9)可以简化成

(10)

其中

所以可以得到

(11)

因为E为负值，并且坐标系中z轴是朝上的，所以这里取负根号的结果。

雅可比矩阵的定义是末端执行机构速度与输入关节速度的线性变换。当执行机构位于工作空间的任意位置的时候，它的矩阵元素会发生变化，它与时间存在一定的关联。它的关系式为

(12)

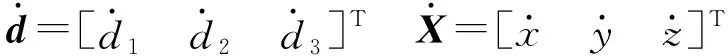
雅可比矩阵通常采用矢量积分和微分变换法求解，对于简单的串联机器人，通常采用微分变换法对方程求导，得到雅可比矩阵。对于复杂的并联机器人，因为运动学方程求导过程复杂，所以通常通过矢量积法进行计算。本文采用矢量积法进行计算，即

(13)

式中Jd——逆向运动学雅可比矩阵Jx——正向运动雅可比矩阵J——雅可比矩阵

2 工作空间分析

2.1 奇异位形分析

对直线驱动并联机器人的奇异行位进行分析，当雅可比矩阵的行列式为零时，并联机械人出现奇异位形，对于式(13)而言，当Jd和Jx中任何一个或者2个矩阵行列式为零，会出现奇异位形。当矩阵Jd不可逆时，机器人出现逆向运动学奇异，当Jx不可逆时，机器人出现正运动学奇异，当矩阵Jd和Jx同时不可逆时，机器人出现组合奇异。下面对3种奇异位形进行讨论：

(1)正向运动学奇异

当此类奇异位形时，数学上求解方程det(Jx)=0并找出所有点是很困难的，可以通过几何关系较为直观地找出所有的奇异位形点。将矩阵Jx看作3个向量，即

(14)

分别提取矩阵Jx的各行，发现各行向量分别对应从动杆l在基坐标系中的空间矢量。

从空间矢量的角度分析机构出现正向奇异性有以下两种可能：①e1、e2、e33个向量均线性相关，这时候会出现共面情况，此时det(Jx)=0，3个矢量的Z分量都为0，动平台与静平台重合，由机构可知不能达到，所以不用考虑，如图4所示。②e1、e2、e33个向量中有3个向量线性相关，如图5所示，此时3个杆件平行，这种情况在结构设计上无法避免，但是可以通过改变驱动电缸与静平台的角度来避免。

图4 三矢量共面图Fig.4 Three coplanar vector figure

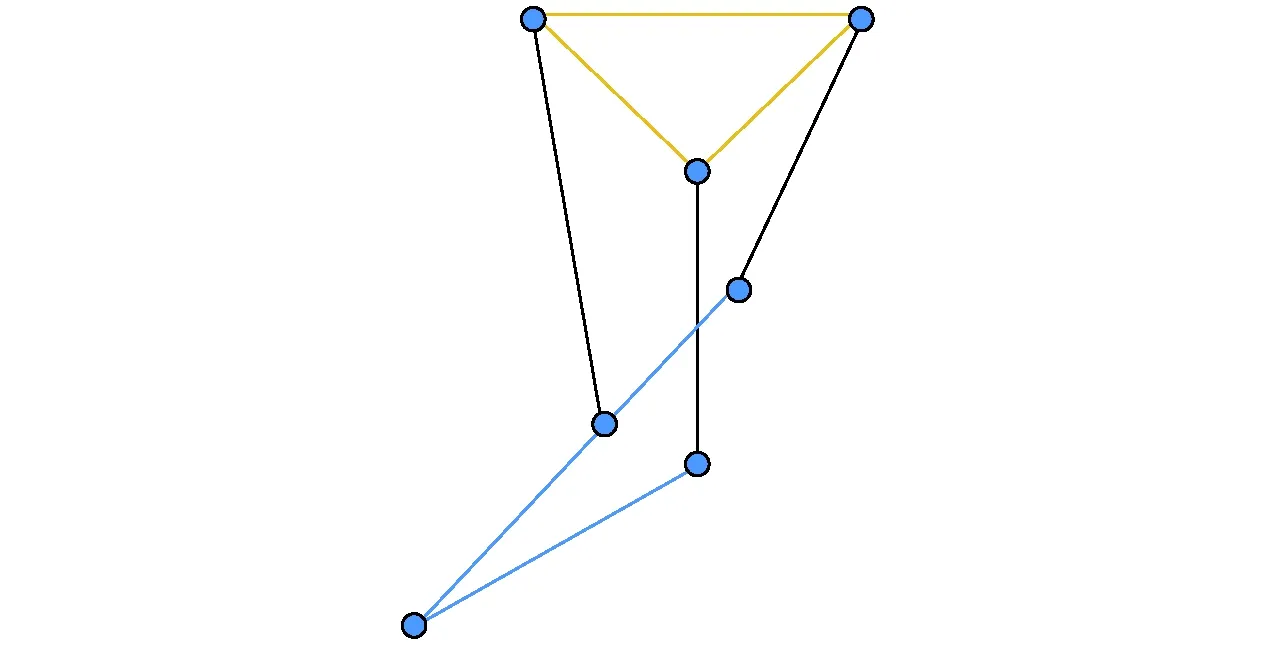
图5 两矢量共线图Fig.5 Two collinear vector figure

(2)逆向运动学奇异

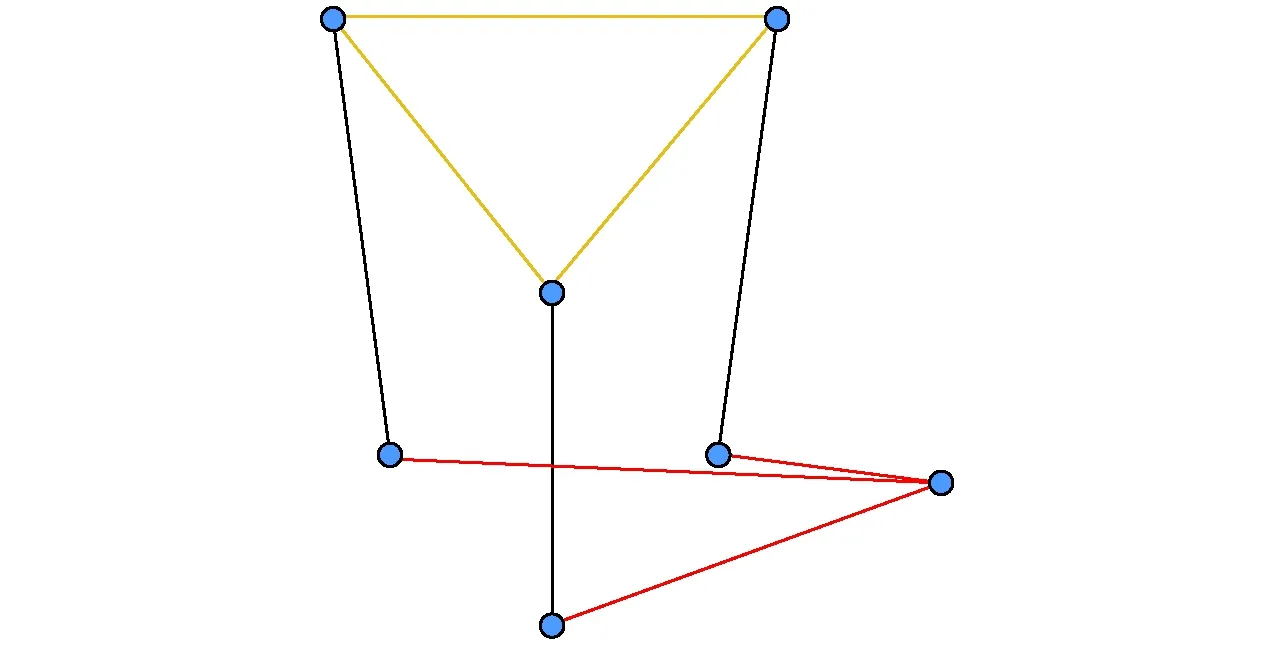
图6 矢量垂直图Fig.6 Vertical vector figure

(3)组合奇异

这种奇异状态从公式上体现就是Jd和Jx同时不可逆，从前面的分析已经得到Jd不可逆的情况在直线驱动并联机器人的机构中并不适用。所以同时出现的组合奇异在此结构中不存在。

2.2 虎克铰约束分析

虎克铰第1自由度的旋转副没有角度限制，可以360°旋转，旋转的速度向量与向量n1同向，n1是平面1的法向量，平面2与平面1垂直，法向量是n2；第2自由度的旋转副有角度限制，它的旋转速度向量始终在平面1内。如图7所示，因为虎克铰的第一自由度的旋转副没有角度的约束，所以虎克铰约束来自于第2自由度的旋转副，根据结构特点，第2旋转副的旋转关于平面1对称，设杆件FiBi与平面1的夹角为γi1，杆件FiBi与平面2的夹角为γi2。如图8所示，根据结构特点与几何关系可知γi2没有角度约束，所以可以得到γi1的角度约束关系为

(15)

根据实际的限制可知，-40°≤γi1≤40°，这样可以得出工作空间的范围。

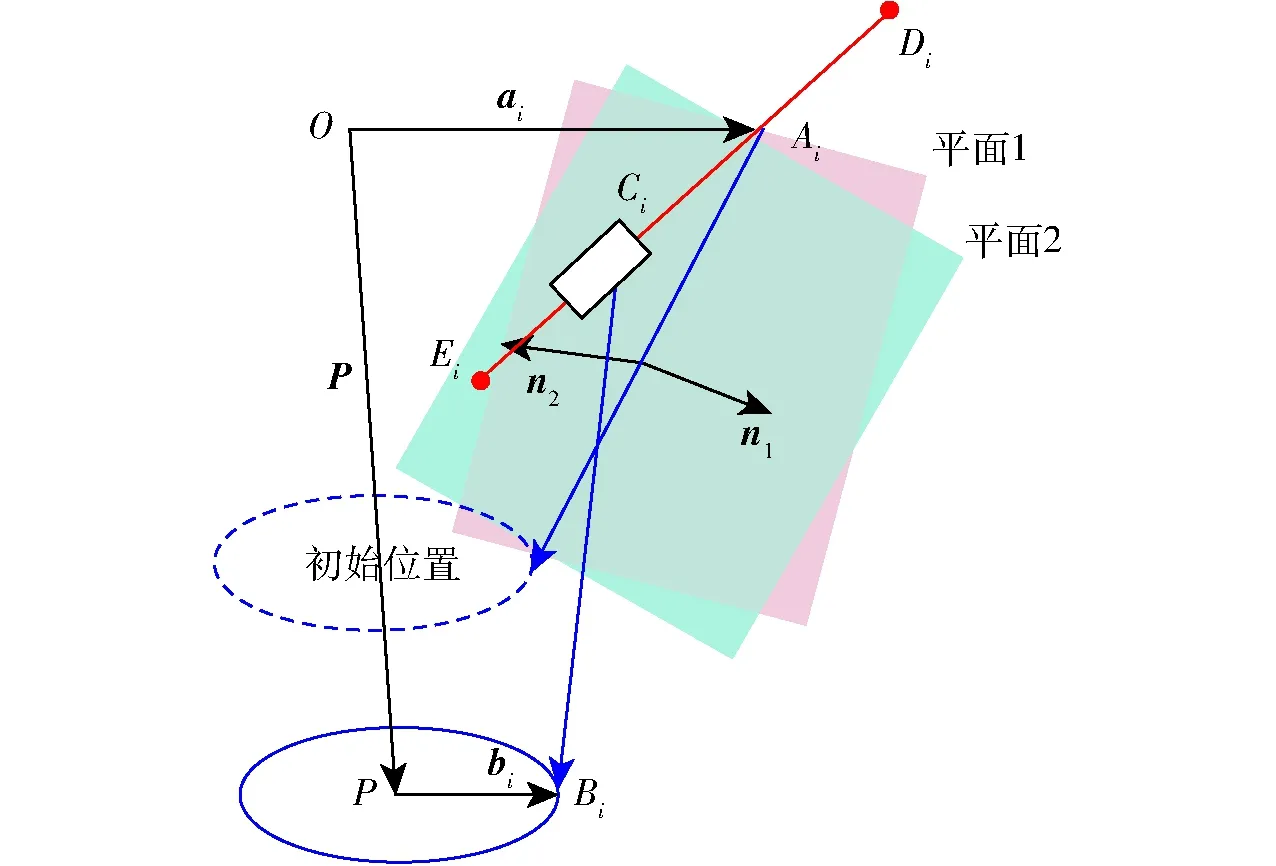
图7 平面法向量1和法向量2Fig.7 Normal vectors of plane 1 and plane 2

图8 虎克铰角度示意图Fig.8 Diagram of Hooke hinge angle

2.3 工作空间求解

为了得到并联机器人的工作空间，本文提出一种极坐标变步长迭代搜索法，其流程图如图9所示，具体的工作空间边界搜索法步骤如下：

(1)通过式(8)和滑块移动副的限制条件确定工作空间的最高点zmax和最低点zmin，并用一系列平行于OXY坐标面的平面将机器人可达工作空间均匀地分割成厚度为Δz的n个子空间，沿着z轴方向进行搜索。

(2)在第i个子空间中，极角从0递增Δθ到2π，极径从初值0开始以固定步长Δρ(稍大)递增到ρ进行搜索。

(3)假设极径递增到第k次，若通过逆解算法求解出的滑块移动副位置由满足条件到不满足条件，则令ρ(k)←ρ(k)-Δρ，Δρ←0.5Δρ，ρ(k+1)←ρ(k)+Δρ；否则ρ(k+1)←ρ(k)+Δρ。

(4)重复步骤(3)，若Δρ≤ε(ε为设定的极径步长精度，ε=0.5 mm)且滑块移动副的位置不满足滑块移动副的限制条件，此时，找到相应极角下的边界点((ρ(k)+2Δρ)zicosθ,(ρ(k)+2Δρ)zisinθ,zi)。

(5)将所有子空间内的边界点搜索出来，然后利用这些点生成并联机器人的工作空间。

图9 极坐标变步长迭代搜索法流程图Fig.9 Program flow chart of polar coordinate variable step iterative search method

通过上面5个步骤，找出构成工作空间外轮廓的所有点，利用Matlab可视化功能，得到图10所示的工作空间。

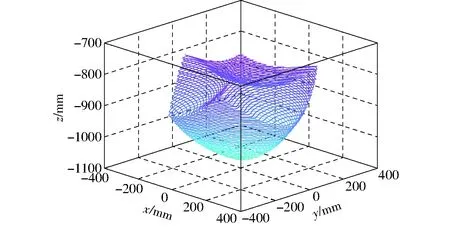
图10 工作空间的Matlab仿真图Fig.10 Diagram of Matlab simulation

2.4 结构参数对工作空间的影响

研究并联机器人工作空间的尺寸与形状对于提高并联机器人的应用。本节重点针对直线驱动型并联机器人的倾斜角、静平台与动平台尺寸、滑块高度等结构参数对进行分析。

由图3可知，并联机器人的结构参数主要包括静平台尺寸a、动平台尺寸b、3个从动杆的杆长l、驱动器与静平台倾斜角α、滑块高度h。为了得到当一个或多个参数变动时结果的表现，针对上面那些设计参数进行参数对工作空间的变化，虎克铰角度的约束范围是±40°，杆长l的初始长度是610 mm，让杆长在510 mm到760 mm之间，以50 mm的增量进行变化。静平台边长a的设计值是1 300.41 mm，让它在1 000.41 mm到1 700.41 mm之间以100 mm的增量进行变化。动平台的边长初始值是103.923 mm。倾斜角α的初始值是38°，让它在25°到90°之间以10°为增量进行变化。滑块高度初始值是98.5 mm，让它在78.5 mm到118.5 mm之间以10 mm为增量进行变化。

工作空间体积也可以定量计算出，如图9所示，当θz增加Δθz的时候，相应的单位工作空间的体积可以表示成

(16)

对式(16)进行积分，可得整个工作空间的体积，表示为

(17)

式(17)可以通过Matlab进行计算求解。

图11 工作空间体积与倾斜角度的关系Fig.11 Relationships of workspace volume vs actuators layout angle

由图11可以看出，驱动器与静平台的倾斜角是一个开口朝下的抛物线，最高点在52°附近，在52°左侧时，体积单调上升。当过了52°时，体积又单调减小，所以选在52°附近时，并联机器人的体积最大。并且不会影响机器人占空间的大小。

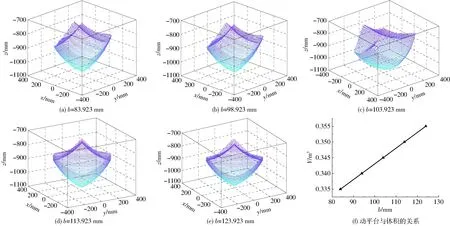
图12 工作空间体积与动平台边长的关系Fig.12 Relationships of workspace volume vs size of moving platform

图12反映了工作空间与动平台边长之间的关系，从图12可以看出，动平台的尺寸对整个机器人的工作空间的形状影响不大，没有出现奇异位置，所以都是合格尺寸。图12还可以看出，动平台边长越大，体积越大，并且呈线性关系，但是，随着边长的扩大，下端的动平台体积也会扩大，对工作环境的要求也就越高，因此不能作为结构参数的首选影响因素。

图13 工作空间形状与静平台边长的关系Fig.13 Relationships of workspace shape vs the size of fixed platform

从图13可以看出，工作空间的形状与静平台存在很大关系的，静平台的边长尺寸过大或者过小都会导致形状变形，也会出现奇异，如图13所示，此时因为静平台边长太小，与动平台边长接近，所以图像上方出现奇异状态，并且图像变形严重，当边长过大时，整个图像会出现上方拉长，下方变大，且奇异区域变多的情况。

每个结构参数对工作空间都有影响，静平台边长与驱动器的倾斜角还有杆长对机器人工作空间的几何形状影响很大。其中静平台边长过大或者过小都会导致几何形状出现变化，甚至会有死点等，所以在选择静平台边长尺寸时，需注意避免过大或者过小，随着边长的增加，体积越大。倾斜角对空间的高度影响很大，随着角度的增加，工作空间的可达高度会变小，空间大小先增加后减小，当达到52°左右时达到最大。在实际运用中，需要根据需要工作空间的大小来选择合适的结构参数，不同参数会导致机器人体积大小的变化，在生产线上，需要在满足任务工作空间的情况下，使机器人占用体积越小，而不是单纯的考虑工作空间的大小。

3 结构参数优化

由直线驱动型并联机器人各机械结构参数对工作空间的影响分析可知，结构参数直接影响到工作空间的大小和形状，因此，有必要对机器人结构参数进行优化，使得其在工作空间内的操作性能更优[15-17]。

3.1 优化模型

为了使优化后的结构参数既能满足给定设计空间的需求，又能使并联机器人的整体外形尺寸尽量小，以及其操作性能更优，定义了一个同时兼顾其操作性能和空间利用率的目标函数

(18)

其中

κ=cond(J)=‖J‖‖J-1‖

式中ω——权重系数(0≤ω≤1)V′——给定设计空间κ——雅可比矩阵的条件数，用来评价并联机器人的操作性能

V*——机器人的可达工作空间

由于雅可比矩阵随着机器人的位形变化而变化，所以用τ衡量机器人在给设计空间中的操作性能，直线驱动型并联机器人结构参数优化可归结为：给定设计空间(设计空间为400 mm×400 mm×100 mm的长方体)，确定静平台边长a，滑块高度h，从动杆杆长L，电缸与静平台之间的夹角α，动平台边长b，使得其空间利用率尽量大和操作性能更优。优化时，各结构参数的变化范围根据文章第3部分各结构参数对应的三维工作空间图和结构参数与体积的关系曲线图确定；此外，必须考虑的约束条件有3支电缸上滑块行程si和虎克铰转角Ui。

由于雅可比矩阵条件数κ越小，表示机器人的操作性能越好，而γ表示空间利用率是越大越好，为了统一，目标函数中取κ的倒数，所以优化的数学模型为

(19)

3.2 优化结果

本文优化算法选择粒子群算法，该算法与诸如遗传算法之类的算法相比，在进化过程中同时记忆位置和速度信息，另外，由于全局最优粒子提供信息给其他的粒子，整个搜索更新过程是跟随当前最优解的过程，因此所有的粒子很可能更快地收敛于最优解。

利用Matlab粒子群优化算法工具箱(PSOt)，对上述数学模型进行求解，其中，根据机器人的实际应用需求，优化求解时， 将权重系数ω分别设置为0、0.5、1等3种情况，结果如表1所示。

从表1可知，ω为0时，即空间利用率最大，ω为1时，即机器人操作性能最优，图14表示了操作性能最优的主视图；图15表示空间利用率最大的仿真图。

表1 优化结果Tab.1 Numerical results of optimization

图14 最优操作性能仿真图Fig.14 Simulation diagram of the best dexterity

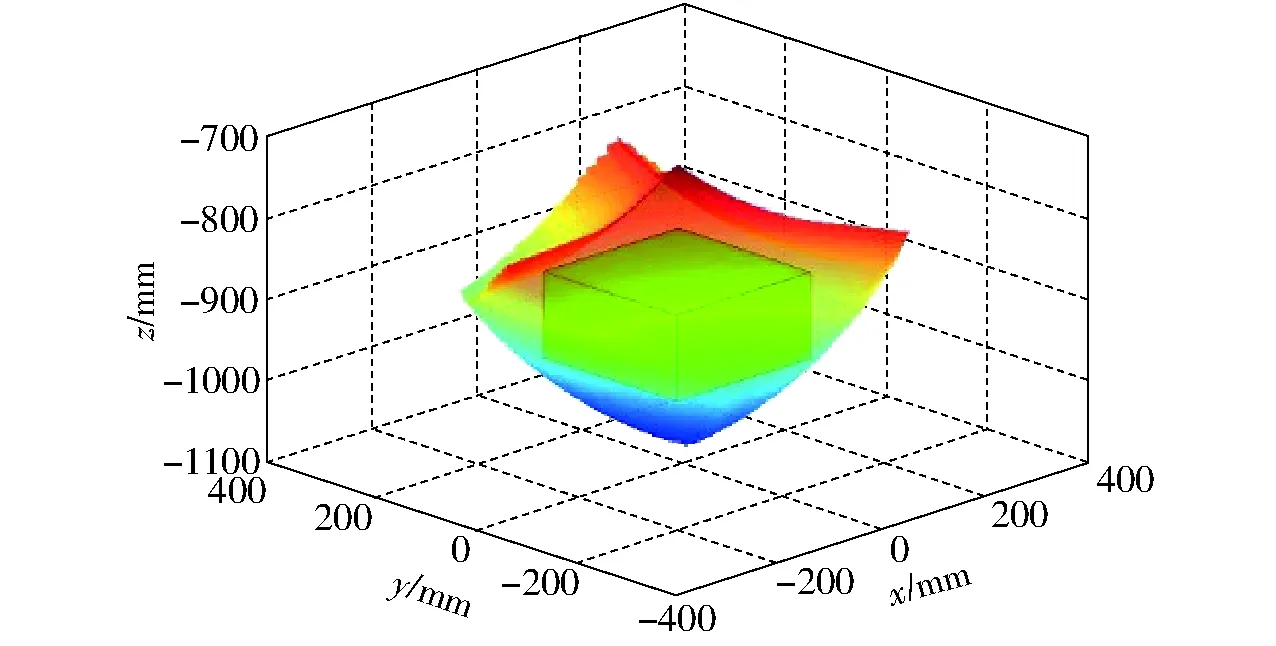
图15 最大空间利用率仿真图Fig.15 Simulation diagram of the best space utility

由图14可以看出，操作性能最优时，长方体占任务工作空间的比重小于最大空间利用率，但是俯视图可以看出长方体边界离工作空间边界较远，运动学性能较优；图15可以看出最大空间利用率的情况时，长方体边界与任务空间边界相交，运动学性能较差。

可以看出不同权重下优化函数指标模型是正确的，根据不同的实际需要，可以选择不同的权重进行参数的筛选。

4 试验验证

为了验证工作空间理论模型的正确性，对直线驱动型并联机器人进行工作空间扫描试验[18-20]。实验所用测试平台如图16所示，采用FARO公司激光跟踪仪Vantage(测试精度为0.015 mm)和相应的辅助装夹设备来实时测量动平台中心的位置。工作空间扫描方式如下：以机器人零点所在的z平面为起始平面，激光跟踪仪分别以x、y轴运动5 mm为一个步长记录下每个点的位置坐标，扫面完一个平面后，z坐标递增20 mm，直至将整个工作空间扫描完成。将每个平面的边界点取出来进行三维空间绘制，结果如图17所示。

图16 机器人工作空间扫描试验现场Fig.16 Scene picture of workspace scan

将图17与工作空间轮廓图10进行对比，外观形状基本吻合，为了进一步地验证，分别取出z=950 mm对应的平面边界点的试验数据和理论数据放一起进行对比，如图18所示，试验和理论数据构成的平面大小、形状基本一致。试验结果表明了工作空间理论模型是正确的，本文基于工作空间理论模型进行的各结构参数对工作空间的影响和结构参数优化的研究是正确的。

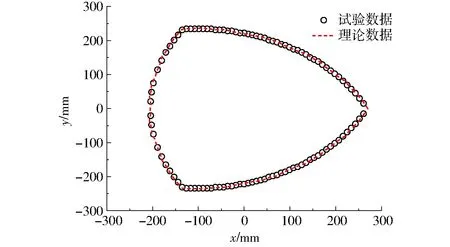
图18 z=950 mm试验和理论数据对比Fig.18 Comparison of theory and test data of z=950 mm plane

5 结论

(1)根据直线驱动型并联机器人的几何模型，利用矢量法建立其运动学模型，并得出机器人运动学逆解和雅可比矩阵。

(2)分析了奇异性和虎克铰对工作空间的约束，提出一种极坐标变步长迭代搜索法求解出机器人的工作空间，并研究得到机器人各结构参数对工作空间的大小和形状的影响趋势。

(3)提出了一种综合机器人灵巧度和空间利用率的全局混合性能指标，建立机器人结构参数优化数学模型，利用粒子群算法对其进行求解，得到不同工况下基于机器人灵巧度和工作空间利用率的最优参数，通过对不同权重下优化得到的参数进行仿真试验，验证了目标函数的正确性和有效性。

(4)将试验扫描出的工作空间轮廓图和理论模型求解出的工作空间轮廓图进行对比，结果表明，工作空间理论模型是正确的，基于工作空间理论模型进行的各结构参数对工作空间的影响和结构参数优化是正确的，为后续的尺度综合研究打下基础。

1 冯李航，张为公，龚宗洋，等. Delta系列并联机器人研究进展与现状[J].机器人，2014,36(3):375-384. FEN Lihang，ZHNAG Weigong，GONG Zongyang，et al. Developments of delta-like parallel manipulators—a review[J]. Robot，2014,36(3):375-384. (in Chinese)

2 BOURI M, CLAVEL R. The linear Delta: developments and applications[C]∥The 41st International Symposium on Robotics, 2010: 1198-1205.

3 JO D Y. Workspace analysis of closed loop mechanisms with unilateral constraints[J].Adv in Des.Automat,1989,3:53-60.

4 GOSSELIN C M. Determination of the workspace of 6·DOF parallel mani Pula-tors[J]. ASME Journal of Mechanical Design,1990,112(3):331-336.

5 MERLET J P. Geometrical determination of workspace of a constrained parallel manipulators[J]. In: ARK, Frnace,1992:326-329.

6 MERLET J P. Determination of the orientation workspace of parallel manipula-tors[J]. Journal of lntelligent and Robotic Systems,1995, 13:143-160.

7 GOSSELIN C M, LAVOLE E, TOUTANT P.Robotics spatial mechanisms and mechanical systems[C]∥22nd Biennial Mechanisms Conference,1992:323-328.

8 MASORY O, WANG J. Workspace evalution of stewart platforms[C]∥22nd Biennial Mechanisms Conference,1992:337-346.

9 BONEY L A, RYU J. A new approach to orientation workspace analysi of 6-DOF parallel manipulators[J]. Mechanism and Machine Theory,2001,36(1):15-28.

10 REZAEI A, AKBARZADEH A, NIA P M, et al. Position, Jacobian and workspace analysis of a 3-PSP spatial parallel manipulator[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(4): 158-173.

11 YU M L, WANG J R, LI J, et al. Kinematics analysis of exoskeletons rehabilitation robot based on ADAMS[C]∥Advanced Materials Research. Trans Tech Publications, 2012, 479: 2333-2338.

12 HARADA T, DONG K, ITOIDAWA T. Design optimization of active scanning probe using parallel link mechanism [J]. International Journal of Precision Engineering and Manufacturing,2012,13(8): 1387-1394.

13 RUGBANI A, SCHREVE K. Modeling and analysis of the geometrical errors of a parallel manipulator micro-CMM[C]∥International Precision Assembly Seminar, 2012: 105-117.

14 崔国华,周海栋,王南,等. 基于Isight的3-UPS-S 并联机器人机构多目标优化[J/OL].农业机械学报,2013,44(9):261-266. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20130945&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2013.09.045. CUI Guohua,ZHOU Haidong,WANG Nan, et al. Multi-objective optimization of 3-UPS-S parallel mechanism based on Isight[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2013,44(9):261-266.(in Chinese)

15 ZHAO Y. Dimensional synthesis of a three translational degrees of freedom parallel robot while considering kinematic anisotropic property[J].Roboties and Computer-Integrated Manufacturing, 2013,29(1)：169-179.

16 梅江平,高奔,谭杨,等.3-SPR并联机构运动学分析[J/OL].农业机械学报，2012,43(8):215-220. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20120839&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2012.08.039. MEI Jiangping, GAO Ben, TAN Yang, et al. Kinematic analysis of 3-SPR parallel mechanism [J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2012，43(8):215-220. (in Chinese)

17 钟琪, 刘贵杰, 王安忆,等. 移动副驱动的Delta机构工作空间分析及机构优化研究[J]. 机电工程, 2015, 32(11):1407-1411. ZHONG Qi, LIU Guijie, WANG Anyi, et al. Workspace resolution and mechanism optimization on Delta parallel mechanism driven by prismatic pair [J]. Journal of Mechanical and Electrical Engineering, 2015, 32(11):1407-1411.(in Chinese)

18 HARADA T, DONG K, ITOIGAWA T. Design optimization of active scanning probe using parallel link mechanism [J]. International Journal of Precision Engineering and Manufacturing, 2012,13(8): 1387-1394.

19 杨继东,万彪刚,高俊东,等.Tripod并联机器人运动学分析与样机实验[J/OL].农业机械学报,2016,47(10):390-397. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20161051&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2016.10.051. YANG Jidong, WAN Biaogang, GAO Jundong, et al. Kinematic analysis and experiment of Tripod parallel robot[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2016,47(10):390-397. (in Chinese)

20 余跃庆,崔忠炜,赵鑫,等.柔顺关节并联机器人设计与实验[J/OL].农业机械学报,2013,44(7):274-278. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20130747&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2013.07.047. YU Yueqing, CUI Zhongwei, ZHAO Xin, et al. Design and experiment of parallel robot with compliant joints[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2013,44(7):274-278. (in Chinese)