结合Beltrami流和递归滤波的高光谱图像分类方法

廖建尚 王立国 郝思媛

(1.广东交通职业技术学院计算机工程学院, 广州 510650； 2.哈尔滨工程大学信息与通信工程学院, 哈尔滨 150001;3.青岛理工大学通信与电子工程学院, 青岛 266520)

0 引言

通过成像光谱仪可以获得达到几百个波段光谱信息的高光谱遥感图像，具有波段多、光谱分辨率高的优点，但是分类结果中椒盐噪声严重影响高光谱图像分类的应用[1-2]。近年来，越来越多学者对在高光谱图像分类中融入空间特征进行了深入研究，目前常见的空间特征提取方法有，形态滤波特征提取[3-4]、马尔科夫随机场特征提取[5-6]、图像分割特征提取[7-8]，其中用滤波器提取高图像纹理信息进行分类逐渐成为一个研究热点。有部分学者用Gabor滤波器[9]提取纹理信息来辅助高光谱分类，HE等[10]通过识别低阶Gabor滤波提取高光谱图像的空间特征，提出了判别式低阶Gabor滤波(Discriminative low-rank gabor filtering, DLRGF)的高光谱图像分类方法；IMANI等[11]采用灰度共生矩阵、Gabor滤波器和形态学滤波器提取空间纹理信息、外形特征和像元邻域信息，并通过不同的特征结合寻找最优的分类算法；JIA等[12]利用Gabor滤波器提取多维数据集特征，联合稀疏表示提出一种有效地空谱结合分类方法GS-MTJSRC；冯逍等[13]按照纹理对不同地物响应的区分度逐一加入三维Gabor纹理特征并辅助光谱信息，用支持向量机(Support vector machine, SVM)进行分类。也有一些学者用双边滤波器[14]来提取高光谱空间纹理信息，如WANG等[15]先用概率SVM获取初始分类结果，然后用双边滤波进行平滑处理，最后用图像分割的方法获取高光谱的分类结果，提高了分类精度。KANG等[16]先用SVM初始分类，再用双边滤波对分类结果进行优化，提出了边缘保持滤波分类方法(Edge-preserving filtering, EPF)； SHEN等[17]用双边滤波器对空谱信息子集提取空间纹理信息，融合后再用极端学习机器对其进行有效分类。还有一些学者用递归滤波[18]提取空间纹理信息，如KANG等[19]用递归滤波对高光谱子集融合后提取空间信息，交由SVM实现分类，提出了图像融合和递归滤波的高光谱图像分类方法(Image fusion and recursive filtering, IFRF)，获得较好的分类结果。另外有不少学者采用了Beltrami流滤波[20-24]进行了研究，Beltrami流应用广泛，但目前没有应用在高光谱图像处理方面的研究报道。

过去在高光谱图像空间纹理信息提取并分类的研究中取得了一定成效，但也存在一些不足：高光谱图像空间分辨率低，空间纹理信息还有待进一步挖掘；地物分布往往具有统一性，在提取空间纹理信息时容易去除像元间的空间相关性。为提高高光谱图像的分类性能，本文提出一种结合Beltrami流滤波和域转换递归滤波的高光谱图像分类算法(BFRF-SVM)，充分利用Beltrami流滤波提取的边缘结构特征和域转换递归滤波提取的空间相关信息，有效辅助SVM进行分类。

1 空间特征提取方法

1.1 Beltrami流滤波提取空间纹理信息

Beltrami流滤波是一种定义在图像流形上的热扩散方程，有清晰的几何意义，可以获取较好的图像边缘信息，对有n个波段的高光谱图像，第i个波段图像Ri的Beltrami流滤波在高光谱的定义为

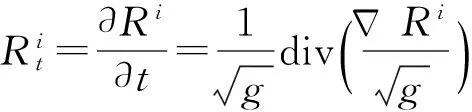
(i=1,2,…,n)

(1)

其中

(2)

(3)

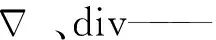
g——度量张量，表示图像曲面的第一基本形式的行列式

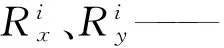
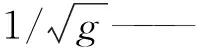
Beltrami流滤波是一种最小化扩散的有效保持图像边缘、结构特点的噪声滤波方法，在图像的噪声平滑与边缘保持方面取得很好的平衡，式(1)的偏微分方程实现基于有限差分离散化，采用欧拉向前差分逼近It和中间偏差逼近空间导数，重新获得Beltrami流滤波公式

(4)

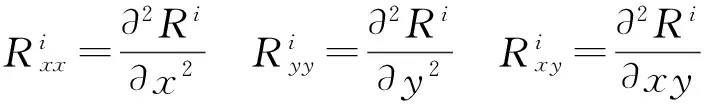
图1所示为印第安林高光谱图像第10波段以及经PCA降维后的第1、2、3主成分滤波前后图像，图2所示为Beltrami流滤波对印第安林高光谱图像第10波段以及经PCA降维后的第1、2、3主成分滤波后图像，由图1、2可以看出，Beltrami流滤波有较好的去噪效果，并能有效获取高光谱边缘结构特性。

图1 印第安林高光谱图像Fig.1 Hyperspectral images of Indian Pines

图2 印第安林的Beltrami流滤波Fig.2 Beltrami flow filtering for Indian Pines

Beltrami流滤波具有较好的图像边缘保持特性，但是在保持边缘的同时容易去除空间相关性信息，本文将用域转换递归滤波[18]来获取空间相关性信息，弥补Beltrami流滤波在图像处理中的不足。

1.2 域转换递归滤波提取空间相关信息

域转换递归滤波是2011年由Gastal等提出的图像特征提取算法，可以将二维的滤波转换为一维的特征提取滤波，对第i个波段的高光谱图像的域转换递归滤波Di(n)在高光谱上的定义为

Di(n)=(1-ad)I[n]+adDi[n-1]

(5)

其中

d=f(yn)-f(yn-1)

(6)

(7)

(8)

(9)

(10)

式中ad——反馈系数I[n]——高光谱图像Di[n-1]——第n-1次递归滤波d——两个相邻像元yn和yn-1在转换域Ωw中的距离

f(yn)——某高光谱波段图像Ri求偏微分后的累加求积分变换为递增函数，将二维图像滤波转换为一维图像滤波

r——滤波半径

σs——空间标准偏差

σr——范围标准偏差

σHt——第t次迭代的数值

N——总迭代次数

该滤波是一个指数衰减的无限冲击响应滤波，当d增大即两像元距离增大时，ad趋于0，阻止链接传播，因此可以保持边缘特性，式(5)并不对称，依赖输入和输出，是一个因果滤波器，为了滤波对称，式(5)需要执行2次，先从左边到右边，再从右边到左边，或者从顶部到底部，再从底部到顶部。

图3所示为域转换递归滤波对印第安林高光谱图像第10波段以及经PCA降维后的第1、2、3主成分滤波后的图像，由图3可以看出，滤波后的图像同类地物灰度相近，说明有一定的相关性。

图3 印第安林的域转换递归滤波Fig.3 Domain transform recursive filtering for Indian Pines

高光谱像元间有较强的空间相关性，为了分析Beltrami流滤波和域转换递归滤波对空间相关性的保持特性，本文引入Moran于1950年提出的Moran’sI指数[25-26]来衡量其高光谱图像滤波前后的空间自相关性，表达式为

(11)

I大代表空间相关性强，I小代表空间差异性大。为了对比两类滤波器对空间自相关性的保持特性，分别对印第安林数据集滤波并计算滤波后的Moran’sI指数且求其均值。如图4所示，域转换递归滤波的大部分Moran’sI指数均值要高于Beltrami流滤波和光谱波段，因此域转换递归滤波可以有效弥补Beltrami流滤波在图像滤波中的不足。

图4 印第安林数据集的Moran’s I指数的均值Fig.4 Average of Moran’s I for Indian Pines

1.3 两种空间信息自适应融合分类

本文用Beltrami流滤波提取的空间纹理信息和域转换递归滤波提取的空间相关性信息，两种信息提取和融合后，由SVM完成分类，形成BFRF-SVM分类算法，实现过程如下:

(1)高光谱PCA降维：对于有l个波段的高光谱数据集R进行PCA降维，选择前面维度的数据组成新的数据集B。

B=Pca(R)

(12)

(2)提取空间信息1：用Beltrami流滤波对PCA降维后的数据集H按照式(4)进行滤波，获取空间信息Dmp。

(13)

(3)域转换递归滤波提取空间信息2：用域转换递归滤波对高光谱数据集R按照式(5)作域转换标准卷积滤波，获取空间信息Dts。

(14)

(4)空间信息线性叠加：Dmp和Dts按照

W=Dmp+Dts

(15)

结合成W。

(5)分类：①从空间信息数据集W中以一定比例随机抽取训练集Ws，其余部分作为测试集Wt。②用径向基函数支持的SVM方法交叉验证，寻找最优参数组合。③用径向基函数支持的SVM对Ws进行训练，获取训练模型。④获取模型后，用径向基函数支持的SVM对测试集Wt进行分类。

BFRF-SVM分类算法流程如图5所示。

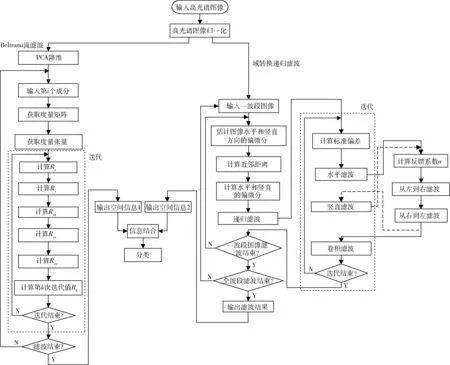
图5 BFRF-SVM算法流程图Fig.5 Flow chart of BFRF-SVM

2 实验数据集

为验证本文提出算法的有效性，采用印第安农林和帕维亚大学的2个高光谱数据集进行验证，其特征如下：①印第安农林高光谱数据集来自机载可见红外成像光谱仪(Airborne visible infrared imaging spectrometer)，是1992年在印第安纳州西北部印第安农林收集到的高光谱遥感图像，具有20 m的空间分辨率，包含144×144个像元，220个波段，由于噪声和水吸收等因素除去其中的20个波段，剩余200个波段，共有16种地物。②帕维亚大学数据集来自反射式光学系统成像光谱仪(Reflective optics system imaging spectrometer)，拍摄于帕维亚大学的高光谱遥感图像，包含610×340个像元，115个波段，由于噪声等因素去除其中的12个波段，剩余103个波段，共有9个类别。

3 实验设计与评价指标

为验证本文所提算法在高光谱分类的优越性，使用7种方法进行比较：①利用文献[27]提出的SVM算法。②利用PCA对光谱信息降维后，用SVM进行分类。③用Gabor滤波器、双边滤波器和导向滤波器分别对高光谱数据用PCA[27]降维后的前20个主成分提取空间信息，并将获取的空间信息和光谱信息线性结合后，用SVM进行分类，形成SGB-SVM、SBL-SVM、SGD-SVM。④文献[15]提出的EPF算法对高光谱图像进行分类，有EPF-B-c和EPF-G-c。⑤文献[19]提出的域转换递归滤波方法IFRF。⑥文献[29]提出的形态学滤波方法SMP-SVM。⑦BFRF-SVM。

本文用整体分类精度(Overall accuracy, OA)、平均分类精度(Average accuracy, AA)以及Kappa统计系数(Kappa statistic, Kappa)来衡量分类算法的精度，为了避免随机偏差，每个实验重复10次记录平均结果，验证平台采用Matlab R2012b，i7-6700 CPU，8GB RAM实验平台。

3.1 参数寻优验证

为了确定Beltrami流滤波参数迭代次数k和时间步长ht，本文采用穷举法，通过前期实验初步估算，限定取值范围，分别为k∈[10,11,…,100]，ht∈[0.01,0.02,…,0.2]，采用印第安农林图像作为实验数据集，分别获取最优分类结果的参数值。先对印第安林数据集进行PCA降维后取前30个主成分作为测试数据集，然后随机抽取数据集的8%作为训练样本和数据集的92%作为测试样本进行验证，实验结果如图6所示。当k=36、ht=0.04，得到分类结果最优：整体分类精度为94.23%，因此本文Beltrami流滤波系数取k=36、ht=0.04。

为了确定域转换递归滤波空间标准偏差σs、范围标准偏差σr、总迭代次数N，使得分类效果达到最优，采用穷举法，限定域转换递归滤波3个参数的取值范围，分别为σs∈[10,14,…,250]，σr∈[0.10,0.11,…,0.20]，N∈[3,4,…,10]，同样采用印第安农林图像作为实验数据集，获取最优分类结果的参数值。随机抽取实验数据集的8%作为训练样本和实验数据集的92%作为测试样本进行验证，实验结果如图7所示，当σs=170，σr=0.18，N=6时，得到的分类结果最优：整体分类精度为94.94%，因此域转换递归滤波系数取σs=170，σr=0.18，N=6。

图6 Beltrami流滤波分类参数寻优Fig.6 Parameter optimization of Beltrami flow filtering for classification

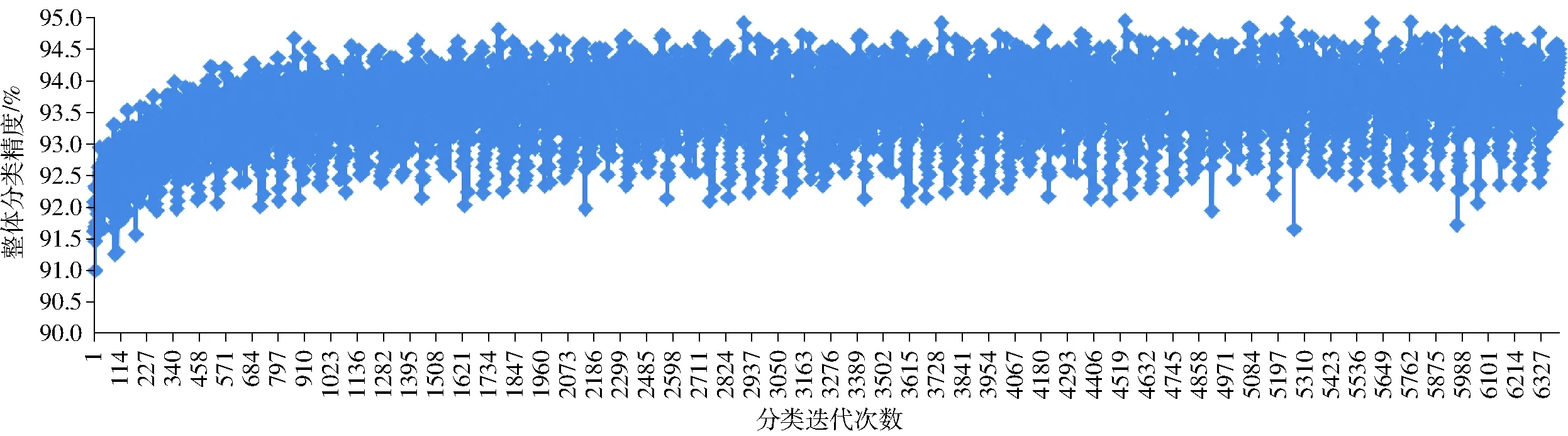
图7 域转换递归滤波分类参数寻优Fig.7 Parameter optimization of domain transform recursive filtering for classification

图8 印第安农林数据集分类Fig.8 Classification for data set of Indian Pines

3.2 实验验证

用7种方法分别对印第安林和帕维亚大学数据集进行分类对比验证，其中验证方法如下：①印第安农林数据集图像，地物分布如图8a所示，选取全部16个类别，每类随机选取7%的样本组成有标签训练集，其余93%作为测试集，地物数量较少的3类随机抽取21%作为训练集。表1为各种分类方法对印第安农林数据集的分类精度统计，分类效果如图8所示。②帕维亚大学数据集图像，地物如图9a所示，选取全部9个类别，每类随机选取3%样本组成训练集，其余97%作为测试集,表2为各种分类方法对帕维亚大学数据集的分类精度统计，分类效果如图9所示。

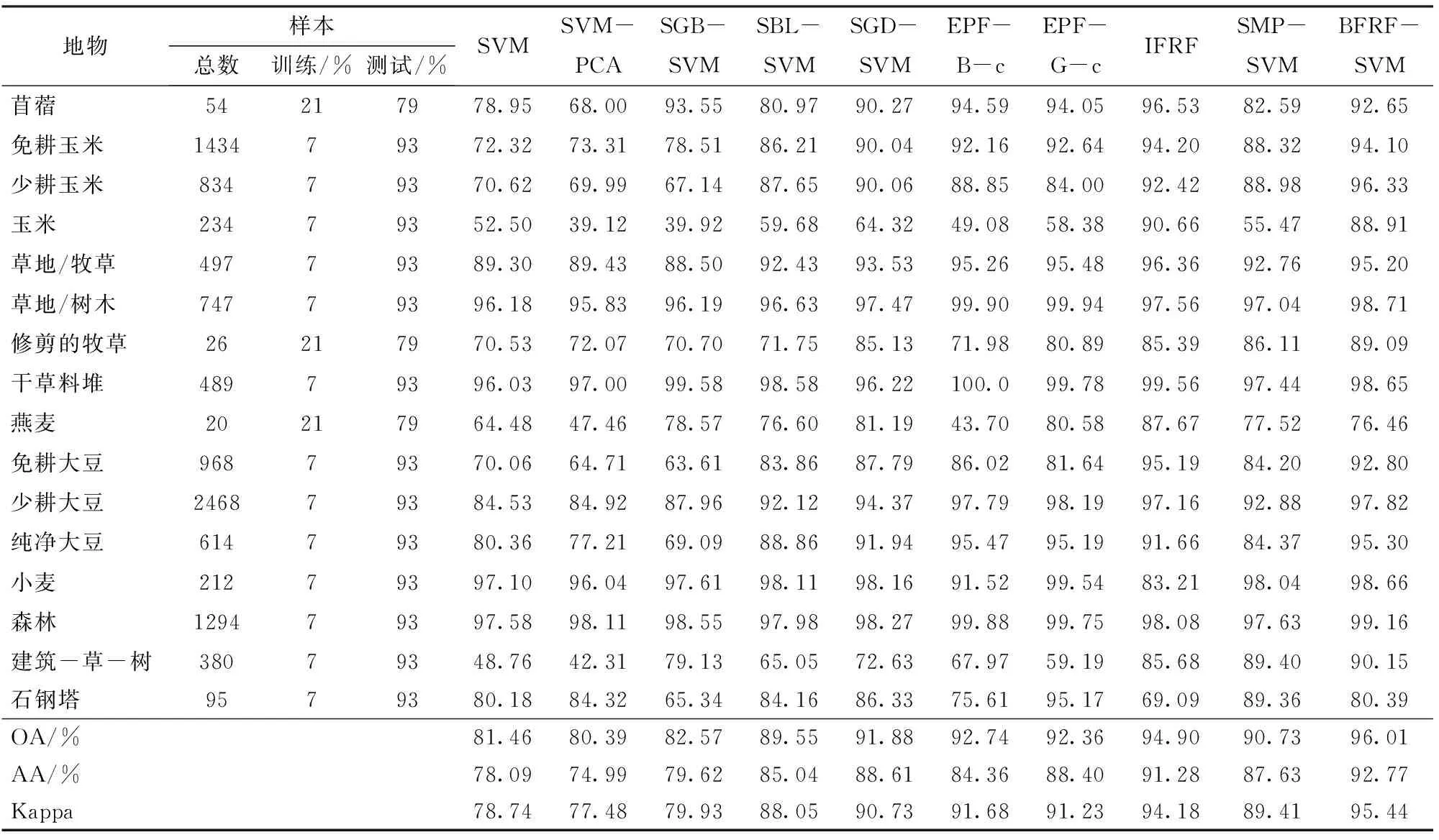
表1 印第安农林数据集图像分类数据统计Tab.1 Classification statistics for data set of Indian Pines

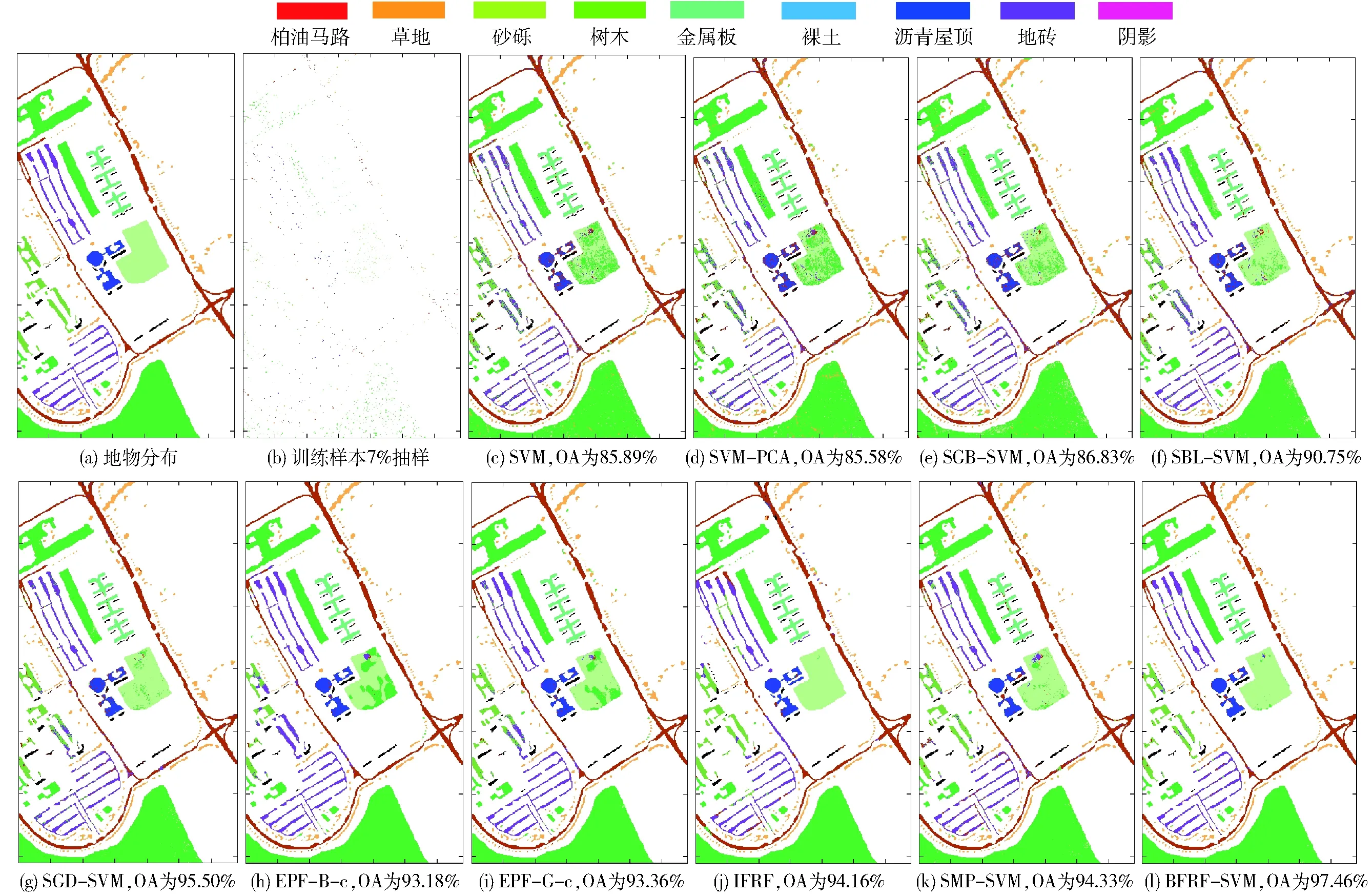
图9 帕维亚大学数据集分类Fig.9 Classification for data set of Pavia University

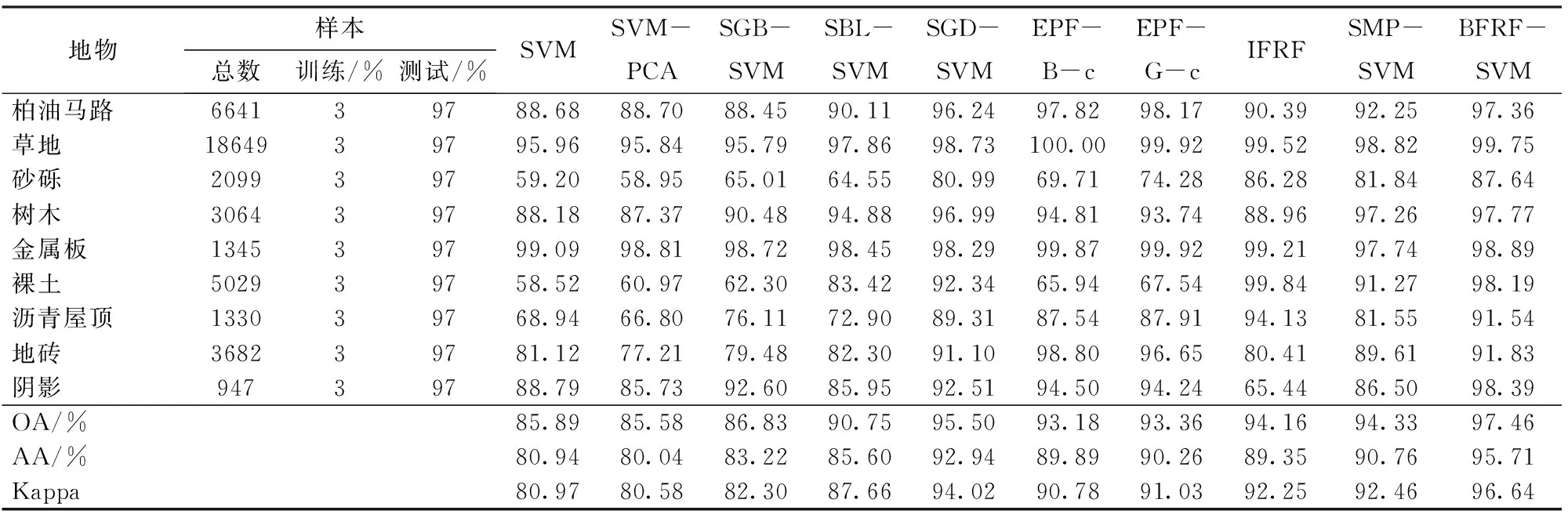
地物样本总数训练/%测试/%SVMSVM-PCASGB-SVMSBL-SVMSGD-SVMEPF-B-cEPF-G-cIFRFSMP-SVMBFRF-SVM柏油马路664139788.6888.7088.4590.1196.2497.8298.1790.3992.2597.36草地1864939795.9695.8495.7997.8698.73100.0099.9299.5298.8299.75砂砾209939759.2058.9565.0164.5580.9969.7174.2886.2881.8487.64树木306439788.1887.3790.4894.8896.9994.8193.7488.9697.2697.77金属板134539799.0998.8198.7298.4598.2999.8799.9299.2197.7498.89裸土502939758.5260.9762.3083.4292.3465.9467.5499.8491.2798.19沥青屋顶133039768.9466.8076.1172.9089.3187.5487.9194.1381.5591.54地砖368239781.1277.2179.4882.3091.1098.8096.6580.4189.6191.83阴影94739788.7985.7392.6085.9592.5194.5094.2465.4486.5098.39OA/%85.8985.5886.8390.7595.5093.1893.3694.1694.3397.46AA/%80.9480.0483.2285.6092.9489.8990.2689.3590.7695.71Kappa80.9780.5882.3087.6694.0290.7891.0392.2592.4696.64

3.3 实验分析

(1)用BFRF-SVM对2种数据集进行分类，其中印第安农林数据集的OA为96.01%，帕维亚大学数据集的OA为97.46%，比SVM整体分类精度高出12～15个百分点，比PCA-SVM整体分类精度高出12～16个百分点，比SGB-SVM、SBL-SVM、SGD-SVM高出2～12个百分点，比EPF算法高出4～5个百分点，比IFRF算法高出1～3个百分点，比SMP-SVM算法高出2～6个百分点，充分验证了BFRF-SVM算法的有效性。

(2)印第安农林数据集的训练样本仅为7%，分类精度OA超过96%，可知BFRF-SVM对分布复杂的高光谱数据有较好的效果；帕维亚大学数据集分类训练样本仅为3%，分类精度OA超过97%，由图8、9可以看出，算法对数据集的分类效果提升明显，有效去除了椒盐现象。

(3)为验证监督数据对算法的影响，选择不同的训练样本测试算法的分类精度。由图10a可以看出，印第安农林总体分类精度在4%的训练样本比例时，OA超过了91%，10%的训练样本时，OA超过了97%；由图10b可以看出，帕维亚大学总体分类精度OA在训练样本为0.5%时超过了90%，在4.5%的训练样本时OA超过了98%，验证了BFRF-SVM算法在低训练样本的情况下也能得到较优的总体分类精度，且有一定的稳定性。

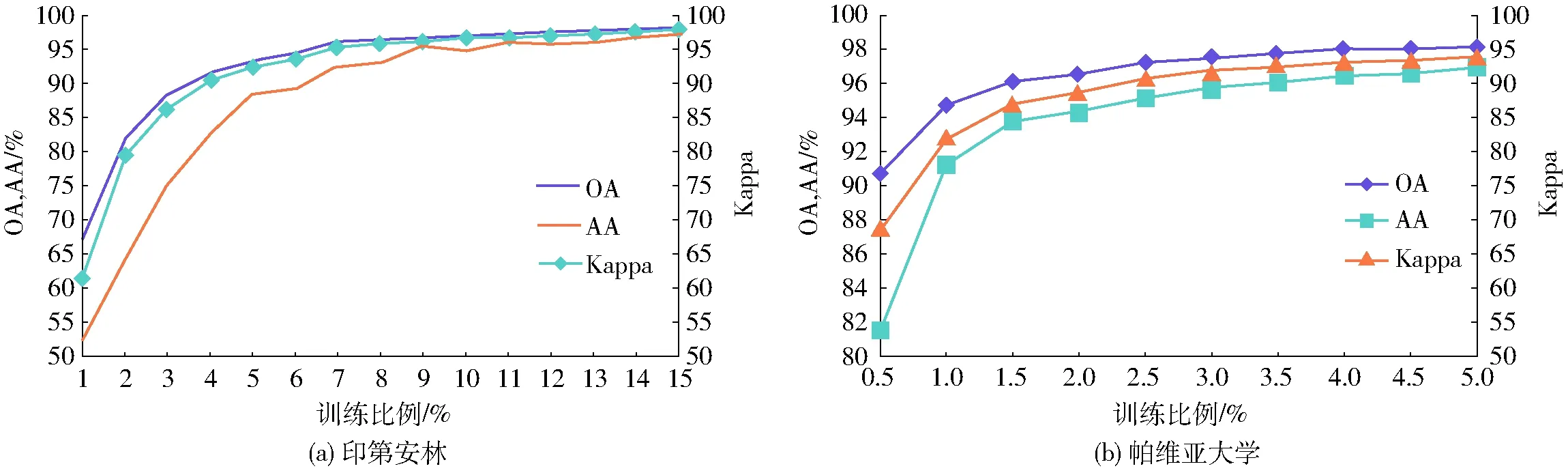
图10 不同训练样本比例分类后OA、AA和Kappa折线图Fig.10 Curves of OA、AA and Kappa with different training samples for classification

4 结束语

提出了用Beltrami流滤波和域转换递归滤波结合的高光谱图像分类算法(BFRF-SVM)，通过一系列实验，验证了BFRF-SVM算法优越性。实验结果表明，本文提出的BFRF-SVM算法与单纯光谱信息SVM算法、空谱结合分类算法、边缘保持分类算法、递归滤波分类算法、形态学滤波算法相比，OA、Kappa和AA都有较大幅度提高，说明了用Beltrami流滤波和域转换递归滤波提取空间信息结合后，能有效提高高光谱图像的分类精度，该算法有以下特点：①用两种滤波器将高光谱图像光谱信息提取为空间信息并进行分类，有效利用了边缘结构信息和空间相关性信息。②Beltrami流滤波提取高光谱图像的边缘结构信息，有效辅助SVM进行像元分类。③域转换递归滤波获得高光谱图像的空间相关信息，弥补Beltrami流滤波中的不足，结合后有效提高了高光谱图像的分类精度。

BFRF-SVM算法为高光谱遥感提供了一种有效的分类方法，可以应用于农作物的精准分类与识别领域。

1 童庆禧, 张兵, 张立福. 中国高光谱遥感的前沿进展[J]. 遥感学报, 2016, 20(5): 689-707. TONG Qingxi, ZHANG Bing, ZHANG Lifu. Current progress of hyperspectral remote sensing in China[J]. Journal of Remote Sensing, 2016,20(5): 689-707. (in Chinese)

2 王俊淑, 江南, 张国明,等. 高光谱遥感图像DE-self-training半监督分类算法[J/OL]. 农业机械学报, 2015, 46(5):239-244. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150534&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2015.05.034. WANG Junshu, JIANG Nan, ZHANG Guoming, et al. Semi-supervised classification algorithm for hyperspectral remote sensing image based on DE-self-training [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015,46(5):239-244. (in Chinese)

3 IMANI M, GHASSEMIAN H. Edge patch image-based morphological profiles for classification of multispectral and hyperspectral data[J]. IET Image Processing, 2017, 11(3):164-172.

4 BAO R, XIA J, MURA M D, et al. Combining morphological attribute profiles via an ensemble method for hyperspectral image classification[J]. IEEE Geoscience & Remote Sensing Letters, 2017, 13(3):359-363.

5 CHEN P, NELSON J D B, TOURNERET J Y. Toward a sparse bayesian markov random field approach to hyperspectral unmixing and classification[J]. IEEE Transactions on Image Processing, 2017, 26(1): 426-438.

6 CAO X, XU L, MENG D, et al. Integration of 3-dimensional discrete wavelet transform and Markov random field for hyperspectral image classification[J]. Neurocomputing, 2017, 226:90-100.

7 ZHANG Z, PASOLLI E, CRAWFORD M M, et al. An active learning framework for hyperspectral image classification using hierarchical segmentation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(2): 640-654.

8 CUI B, MA X, XIE X, et al. Classification of visible and infrared hyperspectral images based on image segmentation and edge-preserving filtering[J]. Infrared Physics & Technology, 2017, 81:79-88.

9 SHEN L, BAI L. Mutual Boost learning for selecting Gabor features for face recognition[J]. Pattern Recognition Letters, 2006, 27(15):1758-1767.

10 HE L, LI J, PLAZA A, et al. Discriminative low-rank gabor filtering for spectral-spatial hyperspectral image classification[J]. IEEE Transactions on Geoscience & Remote Sensing, 2017, 55(3):1381-1395.

11 IMANI M, GHASSEMIAN H. GLCM, gabor, and morphology profiles fusion for hyperspectral image classification[C]∥ Iranian Conference on Electrical Engineering, 2016.

12 JIA S, HU J, XIE Y, et al. Gabor cube selection based multitask joint sparse representation for hyperspectral image classification[J]. IEEE Transactions on Geoscience & Remote Sensing, 2016, 54(6):3174-3187.

13 冯逍, 肖鹏峰, 李琦,等. 三维Gabor滤波器与支持向量机的高光谱遥感图像分类[J]. 光谱学与光谱分析, 2014, 34(8):2218-2224. FENG Xiao, XIAO Pengfeng, LI Qi, et al. Hyperspectral image classification based on 3-D Gabor filter and support vector machines[J].Spectroscopy and Spectral Analysis,2014,34(8):2218-2224.(in Chinese)

14 TOMASI C, MANDUCHI R. Bilateral filtering for gray and color images[C]∥ICCV, 1998:839-846.

15 WANG Y, SONG H, ZHANG Y. Spectral-spatial classification of hyperspectral images using joint bilateral filter and graph cut based model[J]. Remote Sensing, 2016, 8(9):748.

16 KANG X, LI S, BENEDIKTSSON J A. Spectral-spatial hyperspectral image classification with edge-preserving filtering[J]. IEEE Transactions on Geoscience & Remote Sensing, 2014, 52(5):2666-2677.

17 SHEN Y, XU J, LI H, et al. ELM-based spectral-spatial classification of hyperspectral images using bilateral filtering information on spectral band-subsets[C]∥IGARSS 2016—2016 IEEE International Geoscience and Remote Sensing Symposium, 2016:497-500.

18 GASTAL E S L, OLIVEIRA M M. Domain transform for edge-aware image and video processing[C]∥ACM Transactions on Graphics (TOG), 2011, 30(4): 69：1-69：12.

19 KANG X, LI S, BENEDIKTSSON J A. Feature extraction of hyperspectral images with image fusion and recursive filtering[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3742-3752.

20 SOCHEN N, DERICHE R, PEREZ L L. The Beltrami flow over implicit manifolds[C]∥IEEE International Conference on Computer Vision, 2003:832.

21 SHI Y, LAI R, WANG D J, et al. Metric optimization for surface analysis in the Laplace-Beltrami embedding space[J]. IEEE Transactions on Medical Imaging, 2014, 33(7):1447-1463.

22 FERNANDEZ J J, MARTINEZ J A. Three-dimensional feature-preserving noise reduction for real-time electron tomography[J]. Digital Signal Processing, 2010, 20(4):1162-1172.

23 MISHRA K N. An efficient Laplace-Beltrami Spectra based technique for online iris image compression and identification[C]∥2016 International Conference on Control, Computing, Communication and Materials (ICCCCM), 2016: 1-6.

24 TAN M, QIU A. Spectral laplace-beltrami wavelets with applications in medical images[J]. IEEE Transactions on Medical Imaging, 2014, 34(5):1005-1017.

25 MORAN P A P. The interpretation of statistical maps[J]. Journal of the Royal Statistical Society. Series B (Methodological), 1948, 10(2): 243-251.

26 MORAN P A P. Notes on continuous stochastic phenomena[J]. Biometrika, 1950, 37(1/2): 17-23.

27 MELGANI F, BRUZZONE L. Classification of hyperspectral remote sensing images with support vector machines[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(8): 1778-1790.

28 CAI S, DU Q, MOORHEAD R, et al. Noise-adjusted principal component analysis for hyperspectral remotely sensed imagery visualization[C]∥16th IEEE Visualization Conference(Vis2005),2005:119-120.

29 FAUVEL M, BENEDIKTSSON J A, CHANUSSOT J, et al. Spectral and spatial classification of hyperspectral data using SVMs and morphological profiles[J]. IEEE Transactions on Geoscience & Remote Sensing, 2008, 46(11):3804-3814.