转管炮身管组内倾角对炮口扰动的影响分析
曹 渊,邱志明,崔东华,肖玉杰
(海军装备研究院, 北京 100161)
转管炮由多根身管组成,每根身管都有对应的炮闩,炮闩由炮膛外壳体内表面的凸轮槽带动作前后滑动,完成装弹、推弹入膛、击发、抽壳和抛壳的动作。转管炮结构件较多,受力和运动情况复杂,对转管炮自动机结构的研究也比较多。张海洋等基于I-DEAS软件的Mechanism Design模块,完成了某转管炮凸轮曲线槽约束下的闩体在曲线槽约束下的运动学分析[1]。景银萍等对某外能源转管机枪击发机构参数进行了优化设计,利用动力学分析软件ADAMS对某转管机枪的击发机构进行参数化建模,对多个重要的参数进行了敏感度分析,得到各参数最优设计值组合,为武器的改进设计起到指导作用[2]。徐健等对转管炮机心体导轨倾角进行了参数化研究[3]。李强等对转管炮旋转发射惯性对弹丸起始扰动进行了建模分析[4]。转管炮自动机设计时,身管组通常设计有内倾角,但内倾角对炮口扰动的影响规律尚无深入研究。本文基于adams动力学软件和Ansys有限元分析软件,建立了身管柔性的转管炮刚柔耦合动力学模型,进行了火炮连发射击仿真试验,通过对炮膛合力和身管组等效刚强度的分析,发现了身管组内倾角对竖直和水平方向炮口扰动的影响规律。
1 刚柔耦合模型
1.1 物理假设
以某中口径转管炮为研究对象,作如下假设:
1) 火炮与大地固连,不考虑与外界接触;
2) 全炮结构中身管为柔性体,与炮箱固连,其余均为刚体。身管组由前、中套箍相连,均为固定约束。
3) 考虑自动机炮匣导轨与摇架之间、中套箍与支撑炮架之间的接触/碰撞;
4) 反后坐装置为液压弹簧系统,提供的弹簧力和液压阻力分别为摇架和自动机相对位移和相对速度的函数;
5) 在炮匣与炮箱之间添加旋转驱动,模拟火炮转速。
1.2 模型设置
考虑身管组内倾角为0°、0.2°、0.4°、0.6°和0.8°五种情况,自动机其余部分结构保持不变。自动机部分模型如图1所示,忽略了供弹、上架和基座等部分。建立整体坐标系,自动机轴线指向尾部方向为z轴,竖直向上为y轴,水平方向为x轴,取右手系。

图1 自动机部分
图2和图3给出了自动机身管组内倾角为0°和0.8°的正视图和侧视图。火炮射速为600发/min,击发位置点在图2中所示正视图炮箱平面的约5点钟位置。进行2 s,20连发长连射模拟仿真试验。

图2 自动机身管组正视图
1.3 载荷设置
1) 炮膛合力
转管炮将多根身管在圆周方向均匀排列,若有n根身管,则相邻身管之间在圆周上的夹角为360°/n,也就是说前一根身管在击发位置击发后,转过360°/n,下一相邻的身管击发,身管组旋转1周,发射n发弹药。击发起始时刻可以写成旋转角度的函数。

图3 自动机身管组侧视图
沿着身管组的旋转方向,将身管依次进行编号,建立第1根身管与击发位置点的相对角位移测量,记为:MEA_ANGLE,第i根身管与第1根身管在圆周方向相差(i-1)360°/n,根据转速即可得到每根身管与上一次击发时刻的时间差,结合ADAMS中的AINT()和AKISPL()函数[5],炮膛合力的表达式为:
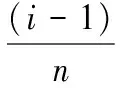
(1)
式中:r为膛底半径;DV为转速参数化变量;i为身管编号;n为身管总数;p_t为膛压曲线,可以通过内弹道计算程序以及装填条件计算获得,也可以通过射击试验测得,本炮的膛底压力随时间变化的曲线如图4所示。

图4 膛底压力随时间变化的曲线
2) 接触力
当两个构件的表面之间发生接触时,这两个构件就会在接触的位置产生接触力。在中口径转管炮系统虚拟样机仿真中,接触力的设定是重要部分,因为自动机的炮匣导轨与摇架之间,以及身管组中套箍与支撑炮架的接触都是产生和影响炮口扰动的重要原因。在火炮武器射击过程中,接触件之间的相对运动较为激烈,因此在模型中选择ADAMS的冲击函数法(Impact)来计算接触力,模型计算公式[5]为:
(3)
式中:F为法向接触力;K为Herts 接触刚度;C为阻尼系数;δ为接触点法向穿透距离;d0为阻尼力过渡区间;Δ=δ/d0;e为不小于1的指数。
2 模拟结果分析
2.1 内倾角对炮膛合力的影响
当身管组内倾角为0°时,炮膛合力沿着Z轴方向,与身管轴线重合,水平x轴和竖直y轴方向的分量为0。当身管组内倾角不为0°时,炮膛合力的方向随内倾角的改变而改变,且与身管轴线重合,此时在水平x轴和竖直y轴方向的分量不为0。
图5给出了内倾角为0.8°时,炮膛合力z轴方向分量的峰值约为1.463 1e6 N。图6给出了内倾角为0.8°时,炮膛合力x轴方向分量的峰值约为12 912 N。图7给出了内倾角为0.8°时,炮膛合力y轴方向分量的峰值约为25 615 N。随着内倾角增大,z轴方向分量减小,x轴和y轴方向分量增大。

图5 内倾角为0.8°时,炮膛合力沿z轴方向的分量

图6 内倾角为0.8°时,炮膛合力沿x轴方向的分量

图7 内倾角为0.8°时,炮膛合力沿y轴方向的分量
2.2 内倾角对炮口扰动的影响
身管炮口扰动体现了火力系统结构对射击精度的影响,身管在发射过程中会发生变形,因此,以身管前端点相对与后端点的形变位移量来表征炮口扰动。
2.2.1 y轴方向的炮口扰动
图8、图9和图10分别给出了内倾角为0°、0.4°和0.8°时,转管炮其中1根身管沿y轴方向炮口扰动变化曲线和5个身管炮膛合力变化曲线的组合图。图11给出了5种内倾角条件下的炮口扰动y轴方向分量的变化曲线。分析结果可得:

图8 内倾角为0°时,炮口扰动沿y轴方向变化曲线和5个身管炮膛合力变化曲线的组合图

图9 内倾角为0.4°时,炮口扰动沿y轴方向变化曲线和5个身管炮膛合力变化曲线的组合图

图10 内倾角为0.8°时,炮口扰动沿y轴方向变化曲线和5个身管炮膛合力变化曲线的组合图
1) 炮口扰动的极值点紧随炮膛合力的极值点出现,表明炮膛合力是引起炮口扰动的外部激励。
2) 极值点过后,在相邻两条炮膛合力的峰值之间,炮口扰动曲线逐步收敛。随着内倾角的增大,扰动收敛的速度先减小后增大。
3) 从图11看出,内倾角为0°、0.2°、0.4°、0.6°和0.8°时,炮口扰动的变化幅值分别约为3.7 mm、4.5 mm、4 mm、5 mm和4.5 mm。随着内倾角的增大,扰动幅值也呈现先减小后增大的趋势。
这是由于影响炮口扰动的原因可以分为外部因素和内部因素。外部因素为炮膛合力,随着内倾角增大,炮膛合力沿y轴方向的分量增大,使得身管y轴方向的扰动幅度增大,收敛速度变慢;内部因素为身管组本身的等效刚强度,身管组由前、中套箍固定,并与炮箱固连,可以认为身管组是一体的,运动是同步的,随着内倾角增大,整体的等效刚强度增大,使得身管的扰动幅度减小,收敛速度变快。基于上述两个因素对身管扰动的影响是相反的,在内倾角增大的过程中,首先内部因素(等效刚强度)占主导作用,扰动减弱,随着内倾角进一步增大,外部因素(炮膛合力的分量)占主要作用,使得扰动增强。因此,随着内倾角增大,炮口扰动先减小后增大。
2.2.2 x轴方向的炮口扰动
图12和图13给出了内倾角为0°和0.8°时,转管炮其中1根身管沿x轴方向炮口扰动变化曲线和5个身管炮膛合力变化曲线的组合图。图14给出了5种内倾角条件下的炮口扰动x轴方向分量的变化曲线。分析结果如下:
1)x轴方向(水平方向)明显小于y轴方向(竖直方向)的扰动幅值,这与火炮射击竖直方向散布大于水平方向散布的规律是一致的。
2) 随身管组内倾角的变化,x轴方向的幅值变化不大。这是由于本身x轴方向的扰动就比较小,而且,在5点钟方向的击发位置点,炮膛合力的y轴分量较大,x轴分量较小,所以导致水平方向的扰动变化不是很明显。

图11 内倾角为0°、0.2°、0.4°、0.6°和0.8°时,y轴方向的炮口扰动

图12 倾角为0°时,炮口扰动沿x轴方向变化曲线和5个身管炮膛合力变化曲线的组合图

图14 内倾角为0°、0.2°、0.4°、0.6°和0.8°时,x轴方向的炮口扰动
3 结论
1) 随着身管组内倾角增大,身管组等效刚强度增大,炮口扰动减小;炮膛合力的水平和竖直分量增大,炮口扰动增强。二者对炮口扰动的影响相反。
2) 在不同身管组内倾角条件下,炮口扰动都是竖直分量较大,水平方向较小,与射弹散布的规律一致。
[1] 张海洋,吕志民,杨宏亮.某型转管炮凸轮曲线槽约束下的闩体运动分析[J].舰船科学技术,2007,29(A01):64-66.
[2] 景银萍,杨臻,李强,等.某外能源转管机枪击发机构参数优化设计[J].振动与冲击,2010,29(12):153-157.
[3] 徐健,薄玉成.转管炮机心体导轨倾角的参数化研究[J].弹道学报,2010(3):26-29.
[4] LI Qiang,BO Yucheng,DUO Yinxian.Influence of Rotating Effect on Initial Bullet Disturbance In Gatling Guns[J].Journal of Ballistics,2005,17(4):88-92.
[5] 李增刚.ADAMS入门详解与实例 [M].北京:国防工业出版社,2014.

