长江江苏段弯曲航道通航能力计算与软件开发

，,c，，

(武汉理工大学 a.航运学院；b.内河航运技术湖北省重点实验室；c.国家水运安全工程技术研究中心，武汉 430063)

随着《关于依托黄金水道推动长江经济带发展的指导意见》的出台，“长江经济带”发展正式上升为国家战略，长江航运经济和沿江经济社会发展将迎来重大机遇，但长江江苏段水域通航环境复杂，交叉航段、弯曲航道众多，如福姜沙航段、尹公洲航段、嘶马弯曲航段等，水上交通事故时有发生。科学地分析长江江苏段弯曲航道通航能力，对降低船舶碰撞与搁浅事故的发生，确保船舶在航道内安全的航行具有重要的意义[1]。同时，作为航道适航程度的重要评价指标，通航能力分析是航道设计和规划的重要依据。

关于弯曲航道通航能力的研究，国外学者在对航道通航能力进行理论研究的同时，根据航道的实际情况提出了相应的经验公式，如西德公式、波兰公式[2]等，国内也有自己的经验公式，如长江公式、苏南公式[3]6等。这些大都是借鉴了国外的公式，是从宏观上研究航道通航能力。还有一些学者从微观上利用船舶航行的航迹带宽度[4- 6]，从平面的角度来计算航道的通航能力。本文提出的弯曲航道通航能力的计算模型，是从微观立体的角度进行分析，综合考虑航道水深、宽度等，构造船舶在无风流影响下船舶所占航宽，运用叠加原理，将风、流致漂移量叠加到无风流影响的公式中去，结合对过往船舶的AIS数据统计分析，得到船舶的吃水、船长与载重吨的关系，最终得到长江江苏段弯曲航道通航能力计算模型。为便于推广本文的研究成果，运用Visual Studio 2010开发了长江江苏段弯曲航道通航能力计算软件，可快速实现不同环境和代表船型条件下弯曲航道上、下行通过能力计算与分析，降低了弯曲航道通航能力计算模型在实际应用中的复杂性。

1 构建弯曲航道通航能力计算模型

1.1 计算原理

1)船舶在无风流影响的情况下，通过弯曲航道的船舶航迹带宽度B1计算公式为

R·cotβ+b/2

(1)

式中：R为弯曲半径，在弯曲航道中航行船舶重心的轨迹圆半径，m；L为船长，m；b为船宽，m；β为船舶的航行漂角，(°)。

2)风、流致漂移量。船舶通过弯曲航道时，受风、流的作用下将会产生横向漂移，此时弯曲航道下行和上行的风、流致漂移量分别为

①风致漂移量[3]。

下行：

[cosαf-cos (αf+θ)]

(2)

上行：

[cosαf-cos (αf+θ)]

(3)

②流致漂移量[7- 8]。

下行：

(4)

上行：

(5)

3)船舶通过弯曲航道所需宽度为

B=B1+BL+BF+2d

(6)

式中：B1为无风流影响时通过弯曲航道的船舶航迹带宽度,m；BL为船舶航行通过弯曲航道时的流致漂移量,m；BF为船舶航行通过弯曲航道时的风致漂移量,m；d为船舶外弦至航道边缘的安全距离,m，d可以选取d=0.4B1。

4)弯曲航道风流作用下的船舶通航能力计算公式。运用叠加原理，把船舶航经弯曲航道的流致漂移量和风致漂移量叠加到无风流的公式中，得到改进后的弯曲航道通航能力计算公式为

下行：

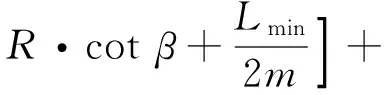
[cosαf-cos(αf+θ)]

(7)

上行时：

(8)

1.2 载重吨与满载吃水、船长定量关系

在采集长江江苏段海量船舶AIS数据的基础上，借助Matlab软件的统计分析功能，定量分析载重吨与船舶满载吃水、船长之间的函数关系。如图1、2所示，载重吨与满载吃水和船舶长度呈现显著的非线性函数关系，可利用二次函数进行高精度拟合。

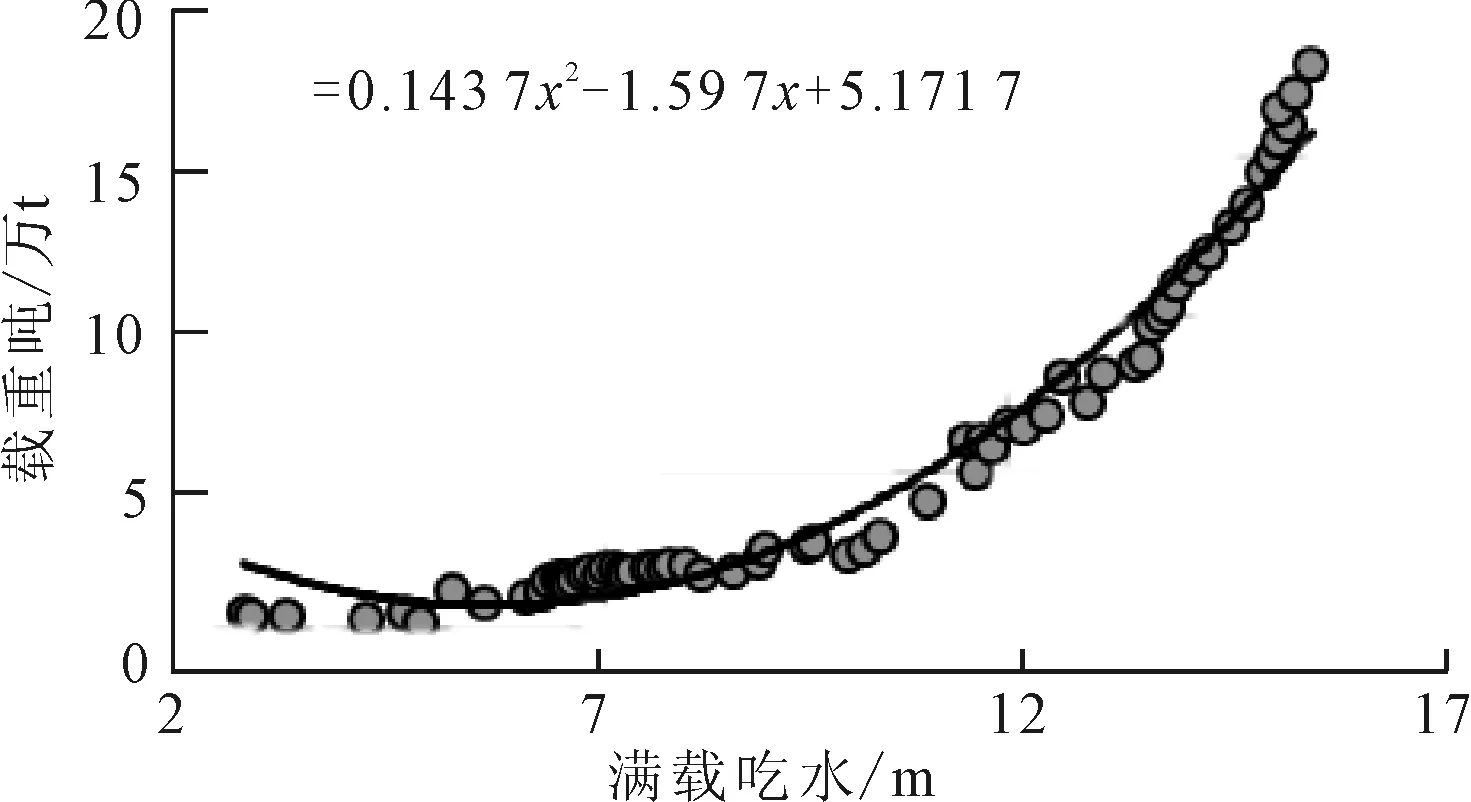
图1 长江江苏段过往船舶载重吨与满载吃水关系拟合图

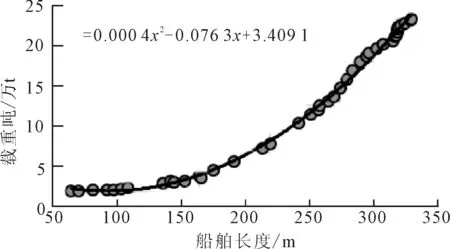
图2 长江江苏段过往船舶载重吨与船舶长度关系拟合图

最终得到以下结果。

1)船舶载重吨与满载吃水的关系为

y=0.143 7x2-1.597x+5.171 7

(9)

式中：y为载重吨，t；x为满载吃水，m。

2)船舶载重吨与船舶长度的关系为

y=0.000 4x2-0.076 3x+3.409 1

(10)

式中：y为载重吨，t；x为船舶长度，m。

3)水深跟通航船舶的关系为

H=h1-Δh

(11)

式中：H为允许通航船舶的吃水；h1为实际水深；Δh为航道剩余水深或航道富裕水深。

根据江苏海事局规定，船舶的实际吃水与富裕水深的关系见表1。

表1 船舶实际吃水与富裕水深对应表[9] m

本文主要目的是确定弯曲航道能通航的最大船舶载重吨和最大船舶长度，根据海事局等部门调研反馈信息，建议此处富裕水深值取1 m。

1.3 具体步骤

步骤1当弯曲航道的实际水位已知时，根据航道等级参照表1确定富裕水深，参照公式(9)、(11)可确定允许通航船舶的实际吃水以及该航段允许通过的船舶最大吨位DWT1。

步骤2当某一弯曲航道的最小航道宽度已知，根据公式(7)、(8)，可以求出允许通过该弯曲航道上下行船舶的最大船舶长度L，再根据公式(9)，长江江苏段过往船舶载重吨与满载吃水关系，就可以用另一种方法求得允许通过该段弯曲航道的最大船舶吨位DWT2。

步骤3将DWT1与DWT2进行比较，选取小者用作该段弯曲航道能够通过的最大船舶吨位。

1.4 软件开发

根据航道的弯曲半径、代表船型的尺度、风流条件，采用上述介绍的计算航道宽度与确定船舶吨位的公式可以计算弯曲航道的通过能力，但是弯曲航道通航能力计算公式较为复杂，而采用通常的计算方法，不但费时而且误差较大。为此，开发了一套长江江苏段弯曲航道通航能力判断软件辅助进行计算，只要选择船舶上行还是下行，输入对应的参数，点击“开始计算”，软件就能计算出能通过弯曲航道的最大船舶吨位及船舶长度。软件运行流程见图3。

1)避免了直接利用数学模型计算长江江苏段弯曲航道通航能力过程中的繁琐细节，提高了通航能力判断的效率，便于推广应用。

2)对于长江江苏段典型的弯曲航道，如福姜沙航道、尹公洲航道、嘶马弯曲航道等，通过调研等方式，得到弯曲航道通航能力计算模型中的相关参数，输入软件，然后由软件自动计算出此航道所能通过船舶的最大吨位以及船舶的最大船长。

图3 长江江苏段弯曲航道通航能力判断软件运行流程

3)对内河船舶来说，可以提前根据自己的预定航线所经过的弯曲航段进行计算，判断能否安全通过，安排航行计划。

2 典型弯曲航段模型参数确定

长江江苏段比较典型的弯曲航段主要有福姜沙航道、尹公洲航道、嘶马弯曲航道等，这些航道是海事部门监管的重要航段，每年都有很多起碰撞、搁浅事故在这些弯曲航段发生，造成了人员的伤亡和财产的损失。参照长江江苏段弯曲航道通航能力计算模型，其中，涉及到航道的参数主要有：航道水深、航宽、弯曲半径、相对风速、流速、风向角、航道等级、弯道中心角，下面对3个主要弯曲航道的上述参数进行介绍。

2.1 福姜沙水道

福姜沙水道由福姜沙北水道、福姜沙中水道、福姜沙南水道3部分组成[10]，见表2。

表2 福姜沙水道参数

2.2 尹公洲航段

如图4所示，尹公洲航段上游下游弯曲航道的弯曲半径是不同的，因此需要分段来进行计算，区段一、区段三航道较为顺直，因此不能作为弯曲航道，在这里不做研究，区段二、区段四航道主要参数见表3。

表3 尹公洲航段参数

图4 尹公洲航段分段示意图

2.3 嘶马弯曲航段

嘶马弯曲航道的主要参数见表4。

表4 嘶马弯曲航段参数

3 数值实验结果

通过对海事局船舶签证信息进行统计分析，得到长江江苏段船舶的长宽比平均值为6.3，船舶速度平均值为8 m/s。以三段典型弯曲航道为实例，按照上述计算方法，利用所设计的软件，分别计算出能通过长江江苏段三个主要弯曲航道的最大载重吨与最大船长。

3.1 福姜沙航段通航能力计算

按照弯曲航道通航能力计算步骤，以福姜沙中水道为例，参照2.1福姜沙中水道的主要参数，船舶长宽比、船速已知，将参数代入软件进行计算(运行结果如图5所示)，得出福姜沙中水道上行船舶可通过的最大载重吨为236 082 t，最大船长为330 m，下行船舶可通过最大载重吨为210 919 t，最大船长为318 m。

同理可得到福姜沙北水道上行船舶可通过的最大船舶载重吨为160 321 t，最大船长为252 m；下行船舶可通过的最大船舶载重吨为156 052 t，最大船长为241 m。福姜沙南水道可通过的最大船舶载重吨为215 262 t，最大船长为318 m；下行船舶可通过的最大船舶载重吨为209 110 t，最大船长为310 m。

图5 福姜沙中水道船舶参数输入运行结果

3.2 尹公洲航段通航能力计算

因尹公洲航段分为4个区段，要通过尹公洲航段，需要综合考虑2个弯曲航段的通航能力，取最小的吨位与船长为该航段的通航能力。参照福姜沙水道的计算方法，将尹公洲航段的主要参数输入，得到的结果为：尹公洲区段二上行船舶可通过的最大船舶载重吨为173 320 t，最大船长为256 m；下行船舶可通过的最大船舶载重吨为165 320 t，最大船长为243 m。区段四上行船舶可通过的最大船舶载重吨为150 265 t，最大船长为235 m；下行船舶可通过的最大船舶载重吨为143 380 t，最大船长为232 m。

3.3 嘶马弯曲航段通航能力计算

参照福姜沙航道的通航能力计算方法，将嘶马弯曲航段的主要参数输入，得到的结果为：

航段上行船舶可通过船舶最大载重吨为256 540 t，最大船长为345 m；下行船舶可通过船舶最大载重吨为238 652 t，最大船长为336 m。

4 结束语

1)软件的计算结果与海事局、船讯网统计资料得到的结果基本相同，证明论文所提计算方法在研究弯曲航道通航能力方面是可信的。

2)长江江苏段弯曲航道通航能力计算模型，既考虑到了前人利用船舶的航迹带宽度，从平面角度分析船舶可否通过航道，还考虑了船舶吨位、吃水、风、流等条件，从一个三维立体的角度出发，综合考虑船舶是否能通过航道。

3)本文把尽可能多的因素考虑进去，但未考虑其他过往船舶的影响、船舶在实际情况中有拖轮的协助、航道资料存在误差以及长江江苏段桥梁造成的影响等。

4)内河船舶可提前根据自己的预定航线所经过的弯曲航段进行计算，判断能否安全通过，安排航行计划。该模型也可应用到对其他河流弯曲航道通航能力的计算。

[1] 程学仨.长江江苏段船舶引航风险分析与控制研究[D].武汉：武汉理工大学,2016.

[2] 万江波.德国内河航道管理[J].江苏交通,2013(9):46- 48.

[3] 饶思梁.内河航道尺度与通航能力关系研究[D].武汉：武汉理工大学,2015.

[4] 刘勇,陈厚忠.顶推船队安全过弯的引航模型研究[J].船海工程,2003(4):45- 47.

[5] 刘明俊,吕习道.船舶过弯道航宽计算及应用[C].中国航海学会内河船舶驾驶专业委员会.中国航海学会内河船舶驾驶专业委员会学术年会论文集.中国航海学会内河船舶驾驶专业委员会，2016.

[6] 孙琦.船舶操纵[M].北京：人民交通出版社,2012.

[7] 曹民雄,马爱兴.内河航道横流对船舶航行的影响[J]. 交通运输工程学报,2008(1):61- 67.

[8] 胡旭跃,王巧洋.内河连续弯曲航道航行漂角分析[J].湖南交通科技,2010(2):179- 183.

[9] 中华人民共和国交通部.内河通航标准GB 50139—2014[S].北京人民交通出版社,2014.

[10] 马国淇.横向环流与福姜沙航道整治[D].杭州：浙江大学,2016.