基于内生网络的银行系统性风险研究
马 钱 挺, 何 建 敏, 李 守 伟, 隋 新
(1.东南大学 经济管理学院,江苏 南京 211189; 2.南京财经大学 金融学院,江苏 南京 210023)
一、引 言
银行是现代金融系统的重要组成部分,也是整个经济系统平稳运行必不可少的金融中介。然而银行危机却时有发生,例如1995年美国巴林银行倒闭,在亚洲、欧洲、美洲地区的金融市场引起强烈波动;2008年法国兴业银行巨亏案导致整个欧洲金融震荡,并波及全球股市。在银行危机中影响最为深远的是银行系统性风险,而系统性风险是一种复杂现象,它的传染效应使得单个银行的风险很有可能演变成整个银行危机。随着银行快速发展,银行同业拆借市场日趋成熟,流动性充足的银行及时贷出资金获得较高收益,流动性不足的银行及时借入资金保证支付,有利于银行自身利润最大化。但银行间通过不断拆借形成复杂的债权债务关系,也为银行系统性风险发生提供了传染途径。一家银行面临流动性问题或者偿还债务困难时,可能会引发该银行破产或倒闭,进而有可能破坏与其他银行间债权债务关系,引发银行大规模倒闭,形成“多米诺骨牌效应”,甚至引发大规模金融危机,影响社会稳定。因此,对银行系统性风险进行深入研究,为我国银行系统性风险监管提供一定的理论基础和实践借鉴。
二、文献综述
近年来网络理论为研究社会经济系统提供了新的视角,也得到了学者们的广泛关注[1-6]。而对于银行经济系统,学者们亦纷纷采用网络理论进行相关研究[7-20]。目前基于外生网络研究较多,主要包括基于随机网络、无标度网络、小世界网络对银行系统性风险进行研究以及不同网络结构对银行系统性风险影响的比较分析。Iori等[7]基于随机网络分析银行间拆借后发现:银行间处于同质情况时,银行间市场对银行系统起到稳定作用;银行间处于异质情况下,银行间系统性风险可能发生,银行间市场稳定作用仍然存在但比较模糊。邓超和陈学军[8]依据复杂网络的Watts级联动力学理论,构建了基于随机网络的金融传染模型,研究显示较大的网络连通度水平不仅为系统性风险发生提供更多传播渠道,而且抵消了风险共享的能力。万阳松[9]101在无标度银行间网络模型基础上对银行主体行为与系统性风险之间关系进行深入研究,研究显示银行市场规模扩大到一定程度上有利于降低系统性风险,银行主体同时参与资金借入和拆出能有效分散自身和其他银行间风险暴露。隋聪等[10]57提出了一种构造无标度网络的方法,研究发现集中度越高的网络由于传染而倒闭的银行数量越多;但当基础违约银行数量不多时,网络集中度越高情况下由于传染而倒闭的银行总资产越少;此外,在集中度高的网络中大银行倒闭引发系统性风险可能性和影响力都大于集中度低的网络;而小银行引发系统性风险可能性远低于大银行,但是小银行倒闭达到一定规模时,可以引发大银行传染倒闭。Godlewski等[11]在小世界联贷市场网络结构基础上研究网络中心度的影响,研究显示小世界网络具有较高聚类系数和较短社会距离,这种网络结构增强银行间社会资本、减少贷款利差并增加借款人财富。许博和刘鲁[12]揭示了随机网络和无标度网络这两种不同网络结构下银行间市场系统性风险发生过程和演化特征,分析了网络结构对于银行系统性风险的影响,指出无标度的银行系统结构会带来更大的系统性风险。李守伟和何建敏[13]基于复杂网络理论,研究了银行间市场随机网络、小世界网络和无标度网络中系统性风险特征及其差异,研究表明:随机性冲击与选择性冲击造成的系统性风险与网络结构以及遭受冲击银行数目密切相关;在这3种网络结构中无标度网络面对冲击时具有最高的稳定性。
由于外生网络事先假定银行网络节点之间连接符合特定的网络结构,这具有一定的局限性。因此,近年来一些学者开始构建内生动态网络模型来研究银行经济系统,如Halaj和Kok[14]提出了银行网络内生形成机制,进而研究市场参数和管理工具改变对银行网络结构和系统性风险的影响。结果显示只有很小比例银行网络中风险传染会减少银行系统平均偿债能力,大部分银行网络其系统性风险发生的可能性可忽略不计。Bluhm和Krahnen[15]通过银行最优决策和市场调节控制方式构建内生动态网络模型,进而研究各种审慎政策下网络演化过程,同时利用Shapley值分析银行面临冲击时对系统性风险的影响以及相应的成本。Lux[16]构建了一个基于银行信用关系的动态网络模型,最初随机地选择交易伙伴,然后通过一个初级强化学习算法形成优惠关系,向经常发生拆借关系的银行提供更加优惠的拆借利率,研究表明优惠利率的实施可以保证周边小银行的存活。王宗尧和隋聪[17]基于银行间拆借关系构建动态网络模型,进而研究银行间资金流动与系统性风险之间的关系,并提出相应的银行间风险传染预警策略。
现有内生网络相关文献仅从存款波动、同业拆借等主体行为进行银行网络构建,而现实中银行主体行为不仅限于上述几种情况,有待进行更深入的研究。对此,本文构建的模型考虑了流动性资产更新、分红与投资、信用拆借以及违约清算等方面,这些都是银行日常经营过程中的主体行为。本文构建的内生网络模型与原有研究相比考虑了更多的银行主体行为,因此更符合实际情况,更有利于从理论层面挖掘银行主体行为与系统性风险之间的内在关联价值。由于银行网络结构对系统性风险有直接或间接的影响[10]57,[21],银行主体行为也对系统性风险起着重要作用[9]1,[22],本文分别从银行网络结构和银行主体行为两个方面来对银行系统性风险进行深入探讨。本文的研究揭示了银行间同业拆借关系的微观行为,丰富了网络视角下系统性风险相关理论基础,同时对于维持经济系统平稳运行、防范系统性风险发生具有一定的理论指导意义和实践参考价值。
三、银行内生网络模型
1.银行资产负债表构建
本文假设银行z资产包括银行间贷款(TLz)、投资(TIz)和流动性资产(Lz),银行z负债包括银行间借款(TBz)、储户存款(Dz)和资产净值(Az)。我们依据Iori等[22]527和Georg[23]的研究构建银行资产负债表,如表1所示:
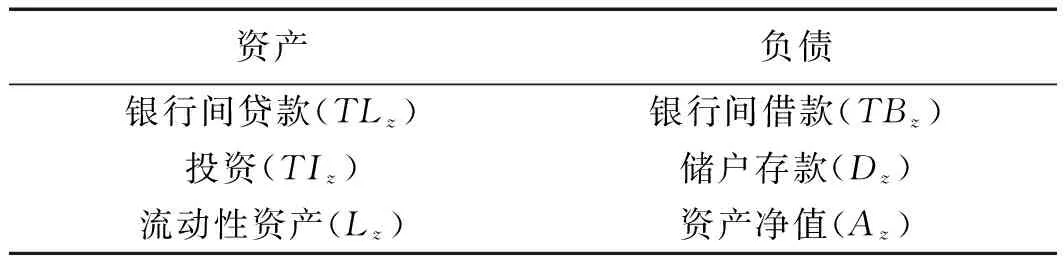
表1 银行资产负债表
(1)

2.流动性资产更新
(2)
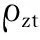
至此,银行z资产净值为:
(3)
3.银行分红
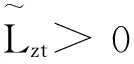
(4)
其中,NetP为银行z净利润;NetP=Azt-Azt-1;h为净利润分红比例;π为法定准备金占存款比例。
4.银行投资
银行分红后若有剩余资金则用于投资。t时刻,银行z投资规模如下所示:
(5)
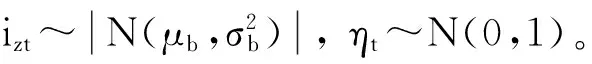
投资后,银行z流动性资金更新为:
(6)
5.银行间同业拆借
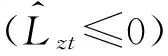
对于债务银行而言,每一个潜在债务银行随机选择一定比例M的潜在债权银行,并观察这些银行所能提供的拆借利率。由于信息不对称及降低交易成本等原因,每一个潜在债务银行更倾向于向旧债权银行寻求信用拆借。但当新的潜在债权银行提供更优惠拆借利率时,其又存在转向新的潜在债权银行进行拆借的可能性。潜在债权银行设定的利率及转向新债权银行的概率分别如下所示[24]:
(7)
(8)
潜在债务银行基于上述交易伙伴选择机制,向流动性充足银行发出借款申请。如果其不能从第一个债权银行获得足够资金,将继续向其他具有额外流动性的银行发出借款申请,直至其资金需求完全得到满足或者银行系统中再无多余流动性可供分配为止。
(9)
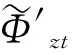
如果债权银行z有充足的流动性,他将满足所有借款银行的借款申请,否则债权银行z将把潜在债务银行按照资产净值从大到小排列,并依次分配其借款资金,直至其再无多余流动性分配为止,对于没有拆借到资金的潜在债务银行将会被新银行代替。
6.银行违约清算
在本文中,银行资产净值小于等于零[24]1636,或者尽管银行z资产净值大于零,但却无法获得足够外部资金使其在随后模拟时刻具有非负流动性[25],此时银行将被移出模拟系统,并进行违约清算。债权银行x″由其债务银行x′违约所产生的坏账为:
(10)
LRx′t=min{max{ϖx′t-Ax′t,0}/TLx′t,1}
(11)
(12)
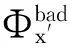
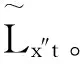
四、仿真分析
1.参数取值
参考Iori等[22]530、Georg[23]2223和Gatti等[24]1637的研究,本文基准模型参数设置如下:假设银行系统中有300家银行,演化周期1000期;在模拟期初银行同质,即初始规模相同,300家银行初始资产净值为2,初始储户存款为8,初始现金流为10;当某个银行破产时,其将被新银行替代,新银行资产净值为区间(0,2)内的随机数。在仿真分析银行系统性风险时,模拟100次,并计算平均每期银行破产数,用来度量银行系统性风险。其他参数设置见表2。

表2 模型的基准参数值
2.网络结构与系统性风险
在上述参数取值下,我们可以得到t=800和t=1000两个时刻的银行网络结构图,如图1和图2所示。从图中可以发现在银行网络中具有多个中心银行,它们与其他一些银行之间形成信用拆借关系,也就是本文构建的内生网络模型具有多中心结构,而多中心结构在金融系统中是存在的,如Lubloy[26]实证研究发现匈牙利支付系统就是多中心结构。
由于网络结构对系统性风险产生重要影响[10]57,[21]1,因此,本文先从银行网络结构视角来对银行系统性风险进行深入探讨。网络节点规模与网络节点异质性属于网络结构研究范畴,网络节点规模的不同可能导致网络结构的改变,网络节点异质性又使得初始状态的网络结构有所差异,因此有必要分别从网络节点规模与网络节点异质性两个维度探究网络结构对系统性风险的影响。
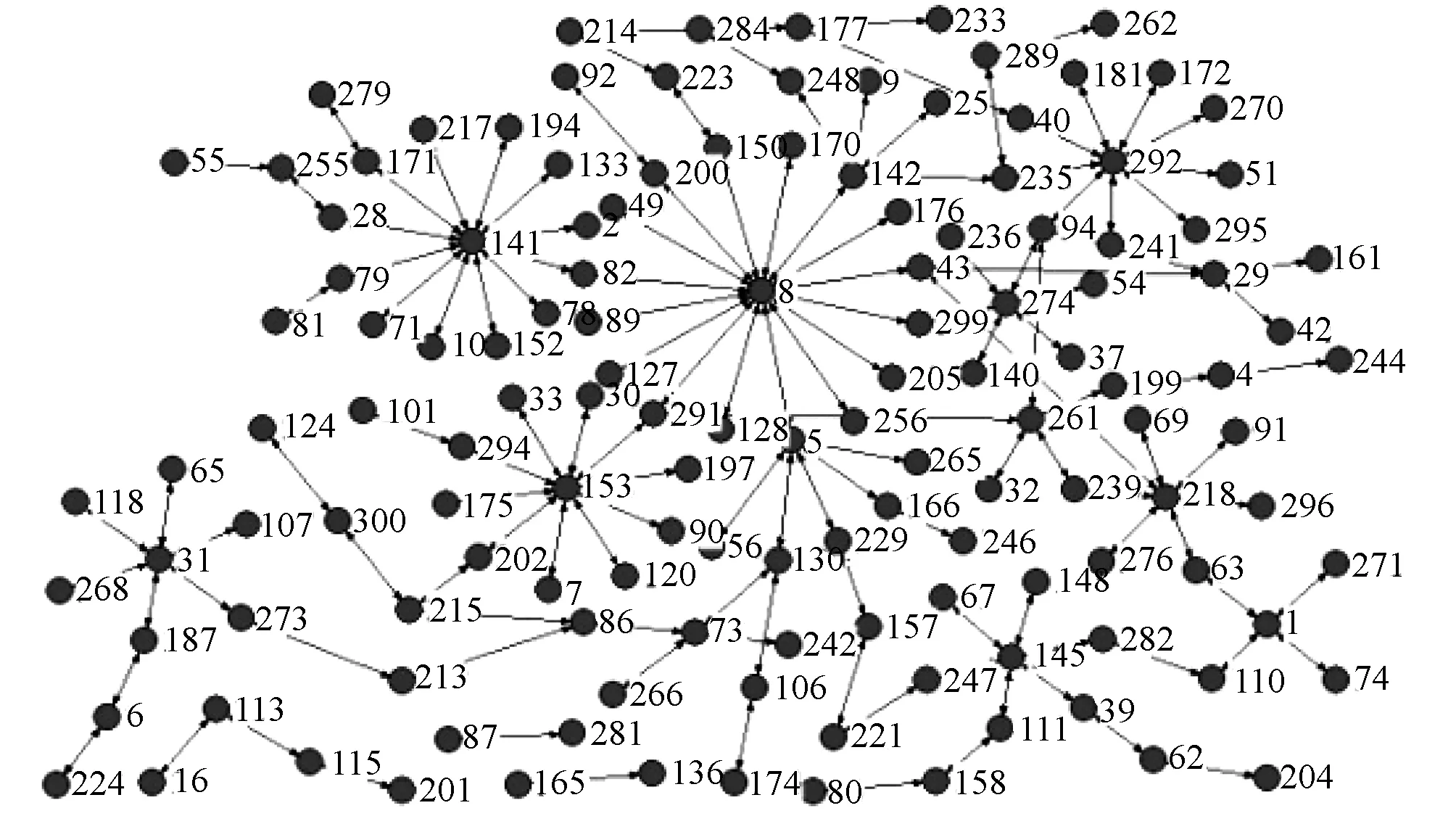
图1 银行网络结构图(t=800)
(1)网络节点规模与系统性风险
随着银行不断发展,银行规模也在不断扩大。由
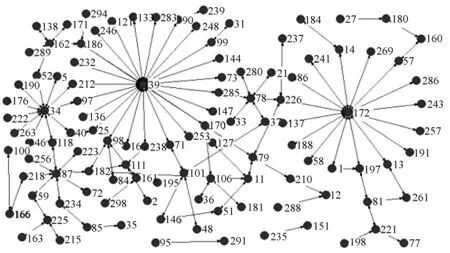
图2 银行网络结构图(t=1000)
于银行间市场新银行的加入,势必会打破原有银行网络结构,影响原有的银行间同业拆借关系,进而可能对银行系统性风险产生一定影响,因此有必要分析银行网络节点规模对系统性风险的影响。选取网络节点规模分别为100,200,300,400家,在每组参数下分别计算平均每期银行破产数,结果如图3所示。
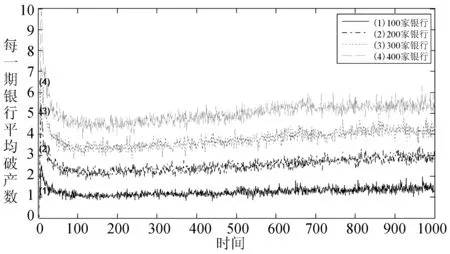
图3 银行规模与系统性风险关系
由图3可知,在某一特定规模下模拟初期银行破产数较多,这是由于数据初始化导致,在运行50期以后,银行系统平稳运行。当网络节点规模为100家时,银行破产数趋于平稳,而当网络节点规模为200家、300家、400家时,银行破产数随着时间推移略有增加。总体来说,随着网络节点规模不断扩大,银行间债权债务关系更加复杂,这增加了银行间风险暴露。一家银行可能同时有很多债权银行和债务银行,一旦这家银行倒闭,便会把违约风险迅速传染给很多银行,进而风险会迅速蔓延至整个银行,其银行破产数会随着银行网络节点规模扩大而增大,系统性风险也随之加大。
(2)网络节点异质性与系统性风险
下面分析网络节点异质性与系统性风险之间关系。网络节点同质是指银行初始规模相同,简记为同质银行,即200家银行初始规模相同;网络节点异质是指银行初始规模不同,把200家银行分为2类(异质银行2类),包括40家大银行和160家小银行;另外,把200家银行分为3类(异质银行3类),包括20家大银行、60家中型银行以及120家小银行。具体网络节点异质性分类情况如表3所示。分别计算3种情况下平均每期银行破产数,结果如图4所示。
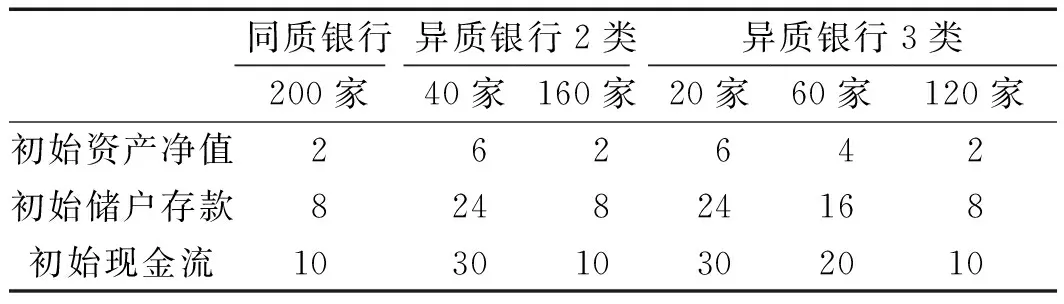
表3 网络节点异质性分类情况表
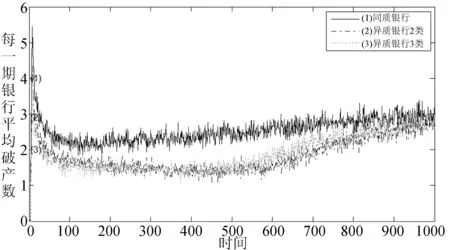
图4 银行异质性与系统性风险关系
由图4可见,模拟初期银行破产数较多,这同样是由于数据初始化导致。在模拟系统运行550期以后,网络节点同质情况下破产数略有增加;而网络节点异质情况下破产数大幅增加,但银行破产数仍低于网络节点同质情况。总体来说,网络节点同质情况下银行破产数多于异质情况,而异质银行分为2类和分为3类之间差别较小。整体而言,银行网络节点同质情况下系统性风险高于异质情况,这表明网络节点异质性对系统性风险具有一定的抵御能力。异质银行相比于同质银行,其银行初始规模不同,在经营活动中规模较大的银行在稳定经营情况下资金会不断累积,形成更大规模银行,当有银行缺少资金时,它就有能力提供充足资金,这样缺乏流动性的银行不会因为无法拆借到资金而倒闭,一定程度上减小了系统性风险。
3.银行主体行为与系统性风险
由于银行主体行为对系统性风险起着重要作用[9]1,[22]525,而拆借对象选择比例、同业拆借利率以及拆借对象转移概率都是银行拆借过程中的主体行为,这些因素的改变一定程度上可能会改变原有的拆借关系,进而可能对系统性风险产生一定的影响,针对此,本文分别从这3个角度来进行深入研究。
(1)拆借对象选择比例与系统性风险
在银行同业拆借过程中,缺乏流动性银行会随机选择一定比例M的潜在债权银行,并观察这些银行所能提供的拆借利率[24]1633,进而选择利率低的银行进行拆借。改变比例M一定程度上会影响到拆借银行的选择,从而影响到整个银行同业拆借过程,进而可能影响到整个银行系统性风险。在本文选取的拆借对象选择比例中,比例M=0.1表示缺乏流动性银行在流动性充足银行中随机选择10%的潜在债权银行,而比例M=1表示缺乏流动性银行向所有流动性充足银行提出借款申请。分别计算不同拆借对象选择比例情况下平均每期银行破产数,结果如图5所示。
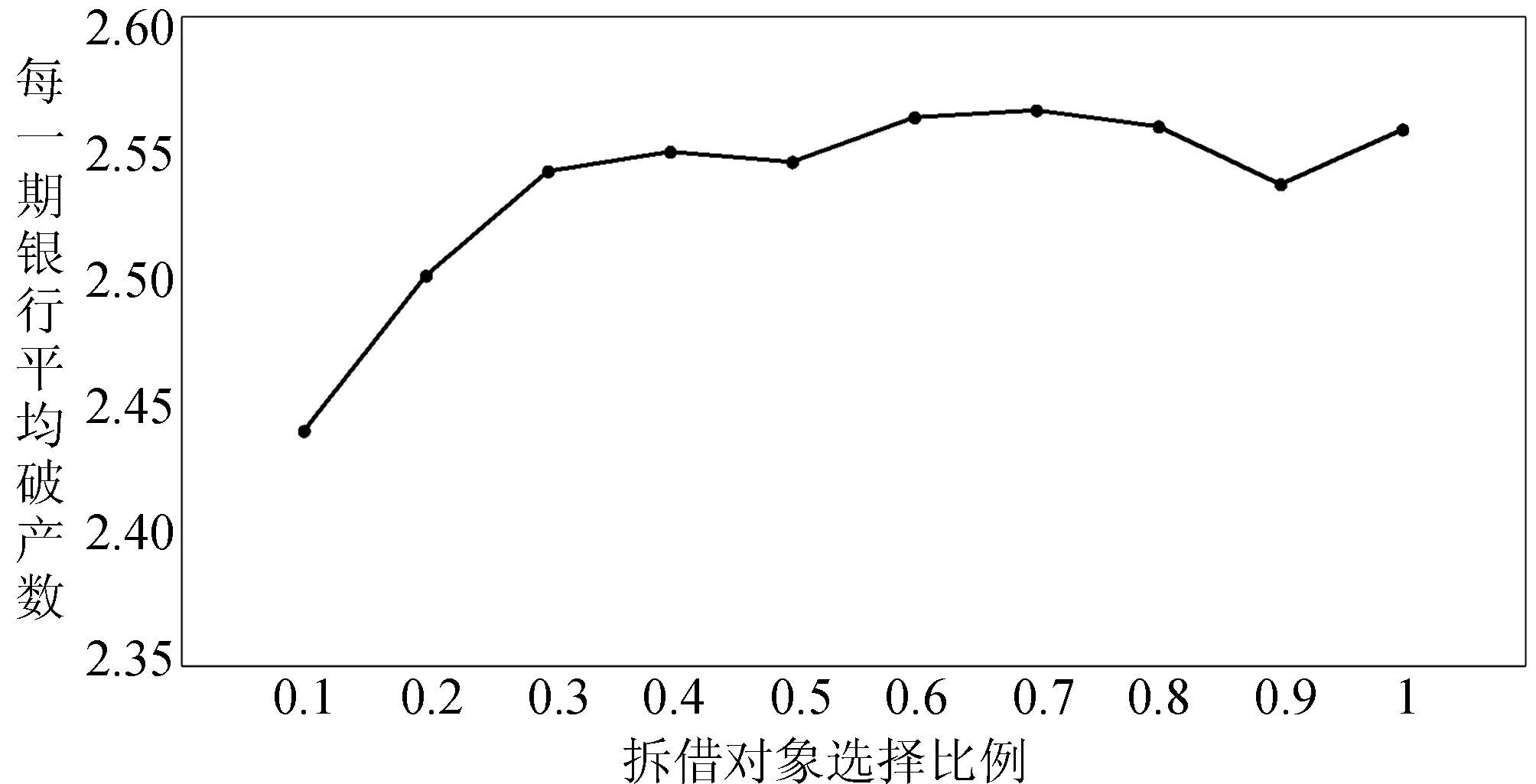
图5 拆借对象选择比例与系统性风险关系
由图5可知,随着拆借对象选择比例从10%增加到30%,银行平均破产数显著增大,其系统性风险也显著增大,而随着拆借对象选择比例继续放大,每期银行平均破产数趋于稳定。由此可知,在选择拆借银行较少时,随着拆借对象选择比例增大,其系统性风险也显著增大,而当选择的拆借银行已经足够多时,继续放大拆借对象选择比例将不会显著影响到系统性风险。由于需要借款的银行都会选择拆借利率最低的银行借钱,随着拆借对象选择比例扩大,很多流动性不足的银行更有可能会向同一家银行借款,那么当这家银行破产时,由于与其发生拆借关系的银行较多,就会使很多关联银行造成一定损失,因此发生系统性风险的可能性较高。而当拆借比例超过30%时,已经形成了很多银行向同一家银行借钱的情况,此时拆借比例继续扩大,其拆借关系相对稳定,不能够进一步加大系统性风险。
(2)同业拆借利率与系统性风险
在银行同业拆借过程中,债务银行向债权银行拆借资金时,会选择最低利率的银行,故债权银行对债务银行设定利率的高低会影响到整个银行同业拆借过程,进而有可能会影响到整个银行系统性风险。为此,有必要探讨同业拆借利率的大小对系统性风险的影响。为了研究同业拆借利率与系统性风险的关系,分析同业拆借利率参数α的变化对系统性风险的影响。在本文参数变化范围内,同业拆借利率参数α与同业拆借利率r正相关。通过对同业拆借利率参数α取不同的值,并分别计算不同α情况下平均每期银行破产数,结果如图6所示。
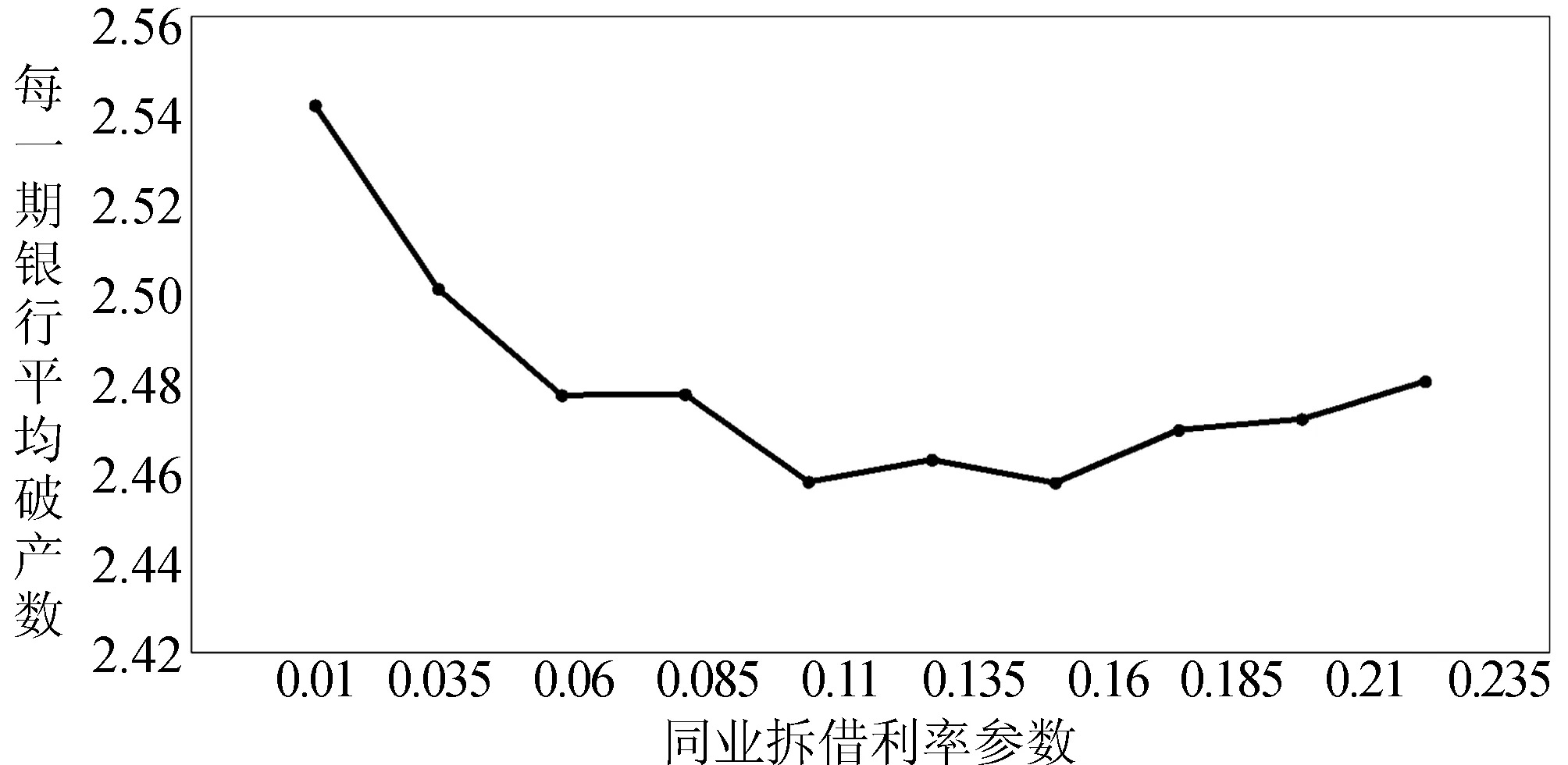
图6 同业拆借利率与系统性风险关系
从图6可得,随着同业拆借利率参数逐渐变大,银行平均破产数先显著减少后略有增加,这意味着随着同业拆借利率提高,银行系统性风险显著降低;但随着同业拆借利率高于某一阈值后继续增大,则银行系统性风险略有增加。当同业拆借利率很低时,会有更多银行愿意借钱,这样形成更加复杂的拆借关系将增加银行间风险暴露,系统性风险较高。随着同业拆借利率逐步提高,一定程度上可以减少银行间拆借,继而减少银行间风险暴露,降低系统性风险。而当同业拆借利率过高时,债务银行将支付高额借款利率,对债务银行而言发生违约的可能性变大,其系统性风险也随之加大。
(3)拆借对象转移概率与系统性风险
在银行同业拆借过程中,由于信息不对称及降低交易成本等原因,每一个潜在债务银行更喜欢和旧的交易对象进行交易[24]1633,即倾向于向旧的交易对象寻求信用拆借。但当新的潜在交易对象可以提供更优惠拆借利率时,其又存在转向新的潜在交易对象进行拆借的可能性。为了研究拆借对象转移概率与系统性风险的关系,需要分析拆借对象转移概率参数λ对系统性风险的影响。其中,拆借对象转移概率参数λ与拆借对象转移概率P成正相关关系。对拆借对象转移概率参数λ分别取不同的值,并分别计算不同λ情况下平均每期银行破产数,结果如图7所示。
由图7可知,随着拆借对象转移概率参数λ从1变化到109,银行平均破产数缓慢增加后趋于稳定,且一直处于2.5与2.55之间,这表明拆借对象转移概率的变化对系统性风险影响较小。随着拆借对象转移概率提高,缺乏流动性的银行更有可能向提供更低利率的新银行借钱,这样提供更低利率的新银行会和更多银行发生拆借关系,一旦这家银行倒闭,将会给很多银行带来损失,其系统性风险增大。但当拆借对象转移概率很高时,缺乏流动性的银行都会向提供利率最低的新银行借钱,这样形成的拆借关系已经稳定,便不能再继续增加系统性风险,即此时系统性风险趋于稳定。整体而言,提供更低利率的新银行与债务银行发生拆借关系后就变成了旧银行,且提供的利率很低,此时即使改变拆借对象转移概率,也未必存在提供更低利率的新银行,原有拆借关系未发生大的改变,因此对系统性风险影响较小。
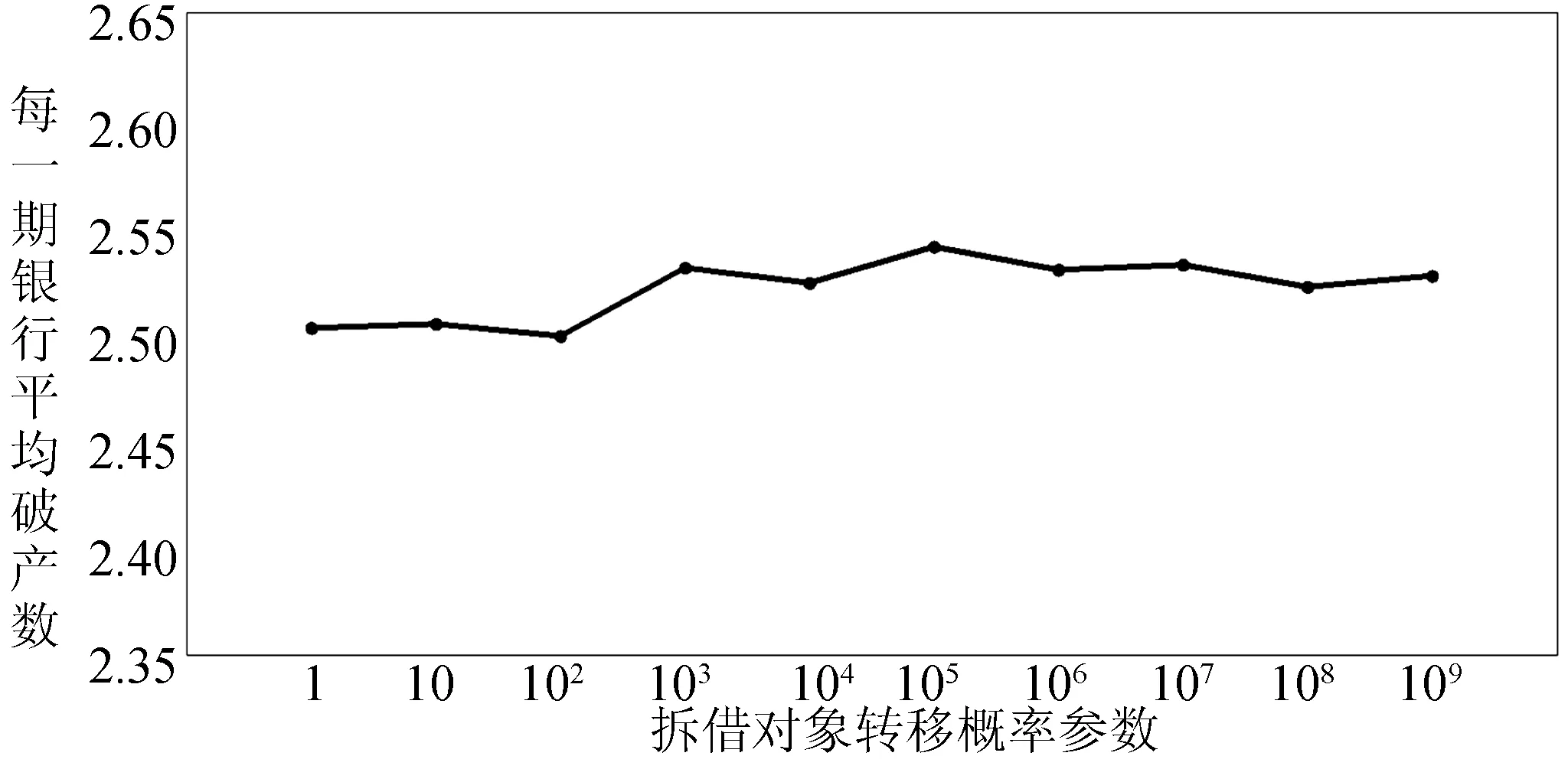
图7 拆借对象转移概率与系统性风险的关系
五、结论与建议
由2007年美国次贷危机引发的全球性金融危机使得系统性风险溢出效应受到普遍关注,这也反映了相关部门对系统性风险监管的重要性及其缺陷。目前我国正不断深化金融改革,扩大金融对外开放,国有银行与外资银行之间联系日益紧密,这些都为银行系统性风险发生提供了可能性。1998年海南发展银行的倒闭则充分说明了中国银行也存在金融风险。因此,研究银行系统性风险,特别是在当前金融系统复杂形态下显得尤为重要和迫切。
对于银行系统性风险的研究,目前基于外生网络研究较多。但由于外生网络事先假定银行网络节点之间连接符合特定的网络结构,这具有一定的局限性。因此,本文基于银行资产负债表构建内生动态网络模型分析银行系统性风险。将银行间市场看作离散时间演化系统,分别从银行流动性资产更新、银行分红和投资、银行间信用拆借以及银行违约清算等方面设定内生网络演化规则。在内生网络模型基础上,分别从银行网络结构和银行主体行为两个方面深入探究其对系统性风险的影响。研究结果表明:在网络结构方面,随着网络节点规模扩大,银行破产数显著增大,其系统性风险也显著增大;在相同网络节点数量下,网络节点同质情况的银行破产数多于异质情况,这表明网络节点异质性对系统性风险具有一定的抵御能力。在银行主体行为方面,拆借对象选择比例提高和同业拆借利率降低都在一定程度上影响整个同业拆借过程进而增大银行破产数,从而使整个银行系统性风险增大;而拆借对象转移概率变化对系统性风险影响较小。
银行网络结构和主体行为在一定程度上都对银行系统性风险产生重要影响。深入了解当下中国现有银行数量及其规模分布,控制银行规模合理增速,平衡国有大型银行与中小银行间的业务发展关系;保持银行间同业拆借利率在合理范围内波动,合理优化相应拆借机制;建立全方位风险监控体系,加强风险控制使银行在保证自身不破产情况下收益最大化,这些都是相关部门亟待解决的问题。上述研究结果对提高银行同业拆借市场抗风险能力、维护银行间金融市场稳定、确保银行系统平稳运行具有一定的理论参考价值和实践指导意义。
[1] 王治莹,李春发. 加权超网络视角下生态产业结构演进研究[J]. 大连理工大学学报(社会科学版),2014,35(1):8-12.
[2] 黄晓,胡汉辉,于斌斌,等. 产业集群式转移的网络结构演化与变迁研究[J]. 大连理工大学学报(社会科学版),2015,36(4):78-85.
[3] 蓝羽石,张杰勇. 基于超网络理论的网络中心化C4ISR系统结构模型和分析方法[J]. 系统工程理论与实践,2016,36(5):1239-1251.
[4]VISMARAS.Equityretentionandsocialnetworktheoryinequitycrowdfunding[J].SmallBusinessEconomics,2016,46(4):579-590.
[5]MOKKY,SHENGQ,YANGRJ,etal.Investigatingkeychallengesinmajorpublicengineeringprojectsbyanetwork-theorybasedanalysisofstakeholderconcerns:acasestudy[J].InternationalJournalofProjectManagement,2017,35(1):78-94.
[6]ZHOUJ,XUW,GUOX,etal.Ahierarchicalnetworkmodelingmethodforrailwaytunnelssafetyassessment[J].PhysicaA:StatisticalMechanicsanditsApplications,2017(467):226-239.
[7]IORIG,MASIGD,PRECUPOV,etal.AnetworkanalysisoftheItalianovernightmoneymarket[J].JournalofEconomicDynamicsandControl,2008,32(1):259-278.
[8] 邓超,陈学军. 基于复杂网络的金融传染风险模型研究[J]. 中国管理科学,2014,22(11):11-18.
[9] 万阳松. 银行间市场风险传染机制与免疫策略研究[D]. 上海:上海交通大学,2007.
[10] 隋聪,迟国泰,王宗尧. 网络结构与银行系统性风险[J]. 管理科学学报,2014,17(4):57-70.
[11]GODLEWSKICJ,SANDITOVB,BURGERHT.Banklendingnetworks,experience,reputation,andborrowingcosts:empiricalevidencefromtheFrenchsyndicatedlendingmarket[J].JournalofBusinessFinanceandAccounting,2012,39(1-2):113-140.
[12] 许博,刘鲁. 银行间市场体系的相继违约风险分析与建模[J]. 系统工程,2011,29(6):42-46.
[13] 李守伟,何建敏. 不同网络结构下银行间传染风险研究[J]. 管理工程学报,2012,26(4):71-76.
[14]HALAJG,KOKC.Assessinginterbankcontagionusingsimulatednetworks[J].ComputationalManagementScience,2013,10(2):157-186.
[15]BLUHMM,KRAHNENJ.Systemicriskinaninterconnectedbankingsystemwithendogenousassetmarkets[J].JournalofFinancialStability,2014(13):75-94.
[16]LUXT.Emergenceofacore-peripherystructureinasimpledynamicmodeloftheinterbankmarket[J].JournalofEconomicDynamicsandControl,2015(52):11-23.
[17] 王宗尧,隋聪. 银行间网络模型与系统风险的分布式预警策略[J]. 系统工程学报,2016,31(6):840-849.
[18] 欧阳红兵,刘晓东. 基于网络分析的金融机构系统重要性研究[J]. 管理世界,2014(8):171-172.
[19] 冯超,王银. 我国商业银行系统性风险处置研究——基于银行间市场网络模型[J]. 金融研究,2015(1):166-176.
[20] 隋聪,谭照林,王宗尧. 基于网络视角的银行系统性风险度量方法[J]. 中国管理科学,2016,24(5):54-64.
[21]ALLENF,GALED.Financialcontagion[J].JournalofPoliticalEconomy,2000,108(1):1-33.
[22]IORIG,JAFAREYS,PADILLAFG.Systemicriskontheinterbankmarket[J].JournalofEconomicBehaviorandOrganization,2006,61(4):525-542.
[23]GEORGCP.Theeffectoftheinterbanknetworkstructureoncontagionandcommonshocks[J].JournalofBankingandFinance,2013,37(7):2216-2228.
[24]GATTIDD,GALLEGATIM,GREENWALDB,etal.Thefinancialacceleratorinanevolvingcreditnetwork[J].JournalofEconomicDynamicsandControl,2010,34(9):1627-1650.
[25]THUMERS,POLEDNAS.DebtRank-transparency:Controllingsystemicriskinfinancialnetworks[J].ScientificReports,2013(3):10-17.
[26]LUBLOYA.TopologyoftheHungarianlarge-valuetransfersystem[R].MNBOccasionalPapers,2006.

