行星轮系侧隙对星载天线指向精度影响分析

李响 赵阳 梁栋 游斌弟

(1 哈尔滨工业大学航天学院，哈尔滨 150001)(2 哈尔滨工业大学船舶与海洋工程学院，山东威海 264209)

卫星可展开天线机构由行星轮系关节实现俯仰和方位运动，在轨工作时，其指向行为和指向精度受到行星轮系关节的装配精度、制造误差等因素影响，且影响具有复杂性与随机性，所以研究天线机构的指向行为和提高指向精度是必要的。

文献[1]根据方位-俯仰型天线建立误差模型，分析天线指向精度受不同误差因素影响程度，探讨了星载天线指向精度的误差源；文献[2]综合考虑多种误差因素影响，利用齐次变换矩阵推导得出了天线指向精度的一般分析方法；文献[3]以某一型天线双轴定位机构为例，从传动、测量、安装、热变形误差等多个方面研究各影响因素的分析模型和计算方法，建立了天线指向精度分析模型。这些研究表明：传动关节间隙对星载天线的指向行为有不可忽略的影响，尤其在微重力环境下，由间隙引起的碰撞更为明显，会影响到系统的整体动力学性能。因此，随着对天线指向精度要求的不断提高，考虑传动关节间隙对天线指向性能的影响尤为重要。文献[4]以某卫星天线双轴传动机构为研究对象，同时考虑方位轴和俯仰轴的关节间隙，利用虚拟样机进行动力学仿真，分析间隙大小对系统运动精度和运行稳定性的影响规律，但其仅通过商业软件定性分析了关节间隙对转动关节的影响特点，因此需要通过数学模型进一步表征间隙对天线机构的影响规律。文献[5]研究间隙等非线性因素对双轴传动机构动力学特性的影响规律，以非线性等效弹簧阻尼模型和库伦摩擦模型为基础，建立了含间隙驱动机构模型，分析间隙大小和驱动力矩对于系统指向精度的影响，但仅仅把关节的间隙等效为孔轴间隙，尚未考虑关节内部传动的齿轮侧隙几何关系变化，因此需要具体考虑行星轮系关节结构参数之间的间隙对系统的影响。文献[6]考虑齿轮侧隙和摩擦的影响，建立了一种行星齿轮箱模型，预测了啮合处受间隙影响及摩擦力激发的动力学行为的耦合影响，发现改变齿对之间的接触载荷，能减小动态传动误差。文献[7]分析了齿轮的动态接触原理，建立了准确的分析模型，用以预测齿侧间隙等导致齿轮传动中撞击和撞击振动的相互作用。文献[8]建立间隙型非线性动力学模型，提出齿轮侧隙会使行星齿轮传动系统出现强非线性动力学特性，并研究齿轮侧隙对于系统运动特性的影响，以及转速、间隙大小等因素对行星轮系动态影响规律，发现了齿轮侧隙大小对于轮齿啮合过程中脱齿和挤齿以及齿面冲击的影响；同时，文献[9-11]进一步考虑齿轮副间多齿轮侧隙、传递误差、啮合刚度等非线性因素建立行星轮系扭转振动模型，研究了啮合误差、多齿轮侧隙等对传动系统非线性动力学行为影响，建立了考虑多齿轮侧隙的行星齿轮传动机构动力学模型。但以上这些文献仅仅从行星轮系作为机构模型角度，分析了间隙对行星轮系振动特性的影响规律，而行星轮系一般作为天线关节传动部件，其振动因素会影响整个展开天线机构运动精度，因此需要从系统角度研究行星轮系作为传动关节时，其啮合侧隙变化对整个系统的影响规律，从根本上揭示天线展开过程的力学特性。

齿轮侧隙是指两个啮合齿轮的工作齿面相接触时，在两个非工作齿面之间形成的间隙，齿轮侧隙变化主要是因为轴孔位置误差引起中心距的变化而导致。本文在上述研究进展的基础上，进一步考虑了行星轮系关节的间隙对天线指向精度的影响，分析了其影响规律，并针对此规律提出了提高指向精度的方法，可为优化星载天线指向行为提供理论基础。

1 行星轮系动力学模型

本文所研究的可展开天线机构的两个关节由2K-H型行星齿轮作为传动部件，如图1所示，可实现俯仰和方位展开运动，以实现指向过程，但由于齿轮之间存在侧隙，其传动过程引起的冲击振动会对整个天线系统动力学特性产生显著影响。因此，为了研究其影响规律，需要对传动关节的具体结构进行描述。

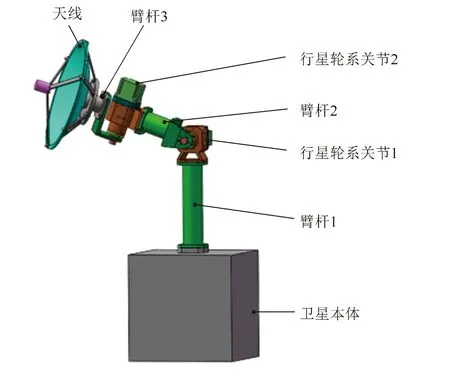
图1 星载可展开天线机构模型图

如图2所示，2K-H行星轮系传动系统由太阳轮、n个行星轮、行星架和内齿轮构成。考虑到行星轮系的结构特点，其系统具有明显的质量集中，因此应用集中参数模型为行星轮系动力学模型。

根据天线的运动特点，行星齿轮呈现了平移-扭转耦合受力特性，因此本文研究的平移-扭转耦合模型，是相对理想的分析模型。根据行星轮系特点和文献[12]，进行合理假设：

(1)各行星轮的物理和几何参数相同，并沿太阳轮均匀分布且各方向上刚度相同；

(2)各齿轮均为渐开线直齿齿轮，忽略各构件柔性变形；

(3)行星轮系的运动在同一平面内，不考虑各构件横向位移。

参照上述假设，建立行星轮系的集中参数模型如图3所示。

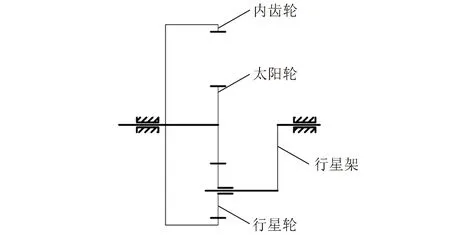
图2 2K-H行星轮系传动系统

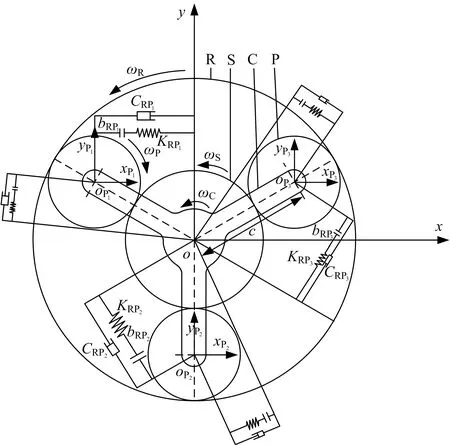
图3 行星轮系集中参数模型Fig.3 Lumped parameter model of planetary gear train

为方便动力学方程的建立，在图3中建立广义坐标oxy，其中太阳轮S为坐标中心，oPnxPnyPn(n=1,2,3)为行星轮坐标系，太阳轮S的角速度为ωS，第n个行星轮Pn的角速度为ωPn(n=1,2,3)，行星架C的角速度为ωC，内齿轮R的角速度为ωR。内齿轮与行星轮之间的啮合刚度为KRPn，啮合阻尼系数CRPn，齿轮侧隙bRPn。每个构件共有3个自由度，系统为2K-H型行星齿轮传动，因此该系统共有3×3+9=18个自由度。

根据图3所示模型，设太阳轮加速度矢量为aS、行星轮加速度矢量为aPn、行星架加速度矢量为aC，内齿轮加速度矢量为aR，则这4个加速度矢量可表示为

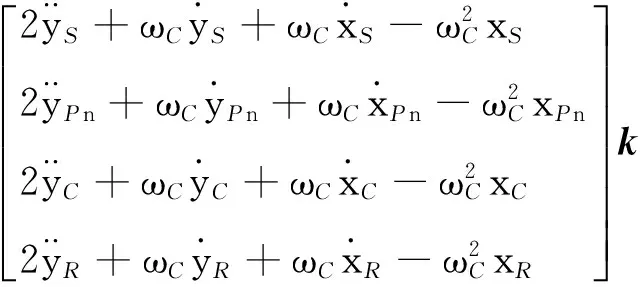
(1)

式中：xi和yi表示构件的横向和纵向位移，i=S、Pn、C和R，分别代表太阳轮、第n个行星轮、行星架和内齿轮；ω表示构件的角速度；j和k分别为x方向和y方向的单位矢量。

当考虑齿轮接触碰撞力的作用下，利用Lagrange方程推导微分方程，可得

(2)

式中：J为构件的转动惯量，Δt为作用时间；n=1,2,3；rbS为太阳轮基圆半径；rC为行星架半径；m为各结构质量；Fe为法向接触力；Ff为切向接触力；α为压力角；TD为输入转矩；TL为负载转矩。

应用等效弹簧阻尼模型求解法向接触力为

(3)

式中：K为等效接触刚度系数；ζ为啮合点法向变形量；e为碰撞回复系数；a为各构件加速度。

根据齿轮侧隙产生原因，首先分析内齿轮与行星轮间的中心距和齿轮侧隙对行星轮系动力学模型的影响，再确定其对系统动力学模型的影响。在行星轮系集中参数模型中，行星轮的动力学参数有：啮合刚度，啮合阻尼系数以及齿轮侧隙，在以往建立齿轮侧隙非线性函数方法的基础上，根据集中参数模型中建立的坐标系，考虑太阳轮与行星轮啮合点的振动位移量为xi和yi，偏转角度为θi，基圆半径为ri，其中i=S,P。为了进一步完善表达式，综合分析中心距c的影响，所以将啮合角φb和重合度εb的变化考虑在内，则太阳轮与行星轮沿着啮合线方向的相对位移为

Δs=rSθS-rPθP+(xS-xP)sinφb+

(yS-yP)sinφb+εb

(4)

其中：

εb=2csinφb-u[(Z1+Z2)(φb-α)cosα+

(Z1+Z2)sinα]

(5)

(6)

式中：u和Z为齿轮模数和齿数。

为了进一步探讨齿轮侧隙对动力学模型的影响，采用齿轮侧隙位移函数表达，齿轮侧隙位移函数与太阳轮和行星轮间的相对位移Δs、内齿轮与行星轮间的齿轮侧隙的大小bRPn有关，齿轮侧隙位移函数为

(7)

2 含侧隙行星轮系的星载天线系统动力学模型

将星载天线系统视为一个多体动力学系统，由卫星本体、天线臂杆、反射面和行星轮系关节组成。卫星本体假设为太空中的一个自由基体，天线假设为一个简单链式多体，其起始端固定在卫星基体上，图4为星载天线示意图。将整个星载天线系统视为刚体且在太空中不受任何外力矩和外力的作用，卫星本体为浮动基座且为受控基，而星载天线的反射面与其末端转轴联结在一起，忽略太空微重力的作用影响，且系统保持动量守恒。

根据模型假设，建立卫星及卫星天线坐标：惯性坐标系原点Or，卫星本体坐标系原点O和各个关节坐标系原点On；旋转关节旋转角为θ1，θ2，θ3等；qog为本体质心到星载天线系统质心矢量；po3为天线转轴的末端位置矢量；qo为本体质心的位置矢量；Og为星载天线系统质心；Bi为臂杆。

将臂杆视为刚体，建立臂杆Bi沿oixi和oiyi方向的振动方程为

(8)

式中：Δθ是臂杆转动的微小角度；qi是臂杆i的质心矢量，Exi和Eyi是xi和yi方向的弯曲刚度，xi和yi是相对于惯性坐标系x和y方向的弹性位移，λxi和λyi是分布载荷，σi是Bi杆的密度，其中i=1,2,3。

利用振型级数逼近的方法可得含行星轮系的天线动力学方程为

(9)

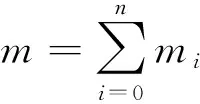
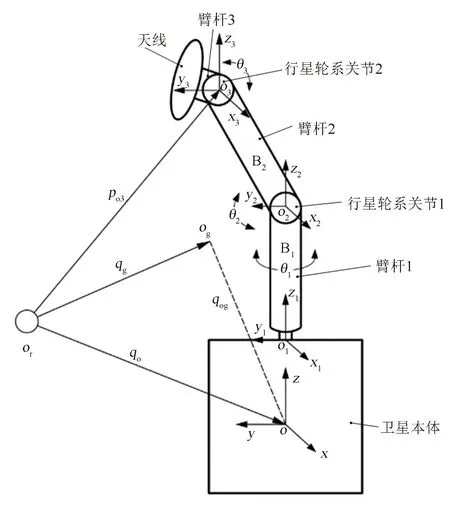
图4 星载天线系统坐标Fig.4 Coordinate axis of satellite antenna

3 数值仿真

基于上述对行星轮系的模型和天线动力学模型的描述，本文采用Newmark数值方法，并通过Matlab软件编程，对间隙因素对指向精度的影响进行仿真分析，行星轮系关节结构的主要参数见表1。

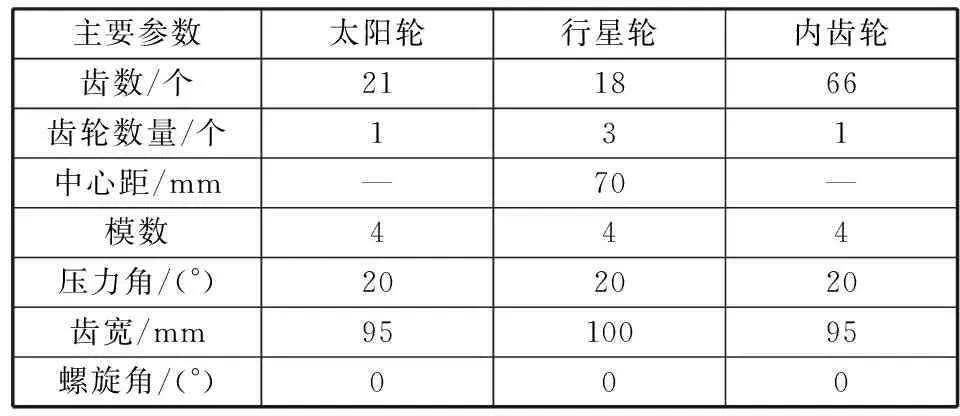
表1 行星轮系主要参数

仿真主要分为单个行星轮系和多个行星轮系对天线动力学的影响两个部分，根据天线动力学模型确定臂杆主要参数(见表2)，并以行星轮系关节作为耦合动力学分析。

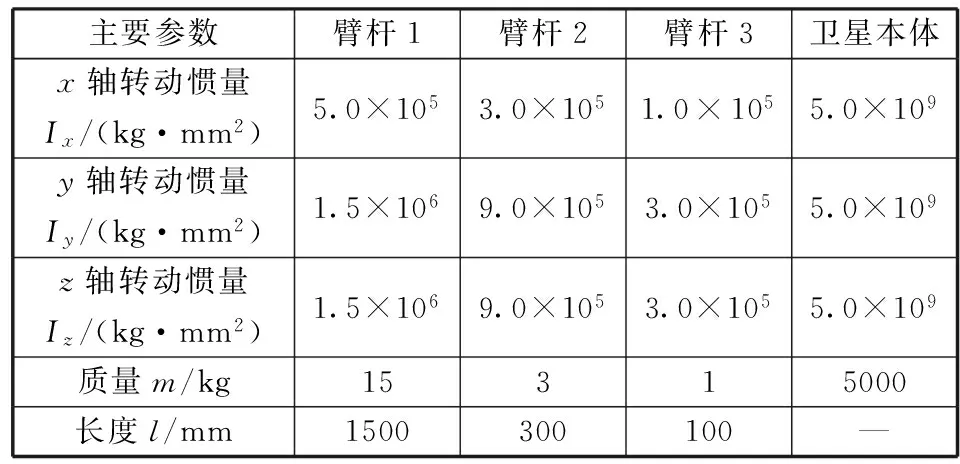
表2 臂杆主要参数

根据表2设置臂杆主要参数，仿真时，太阳轮为主动轮。为其施加驱动，转速为8.0(°)/s仿真时长为5.0 s，初始摩擦系数为0.2，研究天线相对于空间坐标系的波动情况。

侧隙对天线动力学的影响主要分为太阳轮与行星轮啮合的相对位移和行星轮与内齿轮啮合的齿轮侧隙，根据第2节对齿轮侧隙及相对位移计算的分析，分为0 mm(理想状态)、0.05 mm、0.10 mm、0.15 mm和0.20 mm五种不同情况进行动力学仿真分析。

为考虑单个行星轮系的不同齿轮侧隙大小对天线动力学的影响，分析天线相对于理想状态(齿轮侧隙为零)的运动偏差，仿真结果如图5所示。由式(4)～式(7)可知，行星轮与内齿轮的齿轮侧隙bRPn和太阳轮与行星轮啮合的相对位移Δs变化，会导致齿轮侧隙位移f(Δs)波动，由于臂杆等构件传递波动，导致天线的指向与理想位置的偏移量增大。仿真结果符合这一趋势，当运动开始时，天线偏移量出现大的峰值，在0.5～0.7 s之后，偏移量回落到一个较小值，之后随着时间的增加，偏移量也逐渐趋于平稳，整个过程呈现周期震荡趋势。当单个行星轮系的齿轮侧隙为0.05 mm和0.1 mm时，最大偏移量分别为0.05 mm和0.08 mm。而当齿轮侧隙大于0.15 mm时，偏移量会出现大幅波动，偏移量超过0.14 mm。表明：由于存在较大的齿轮侧隙，会导致行星轮系的轮齿啮合出现脱齿现象，使得齿轮啮合精度下降，传动效率降低。因此，应该尽量减小齿轮侧隙，以提高齿轮精度。

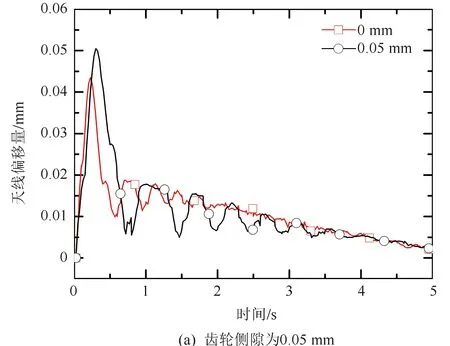
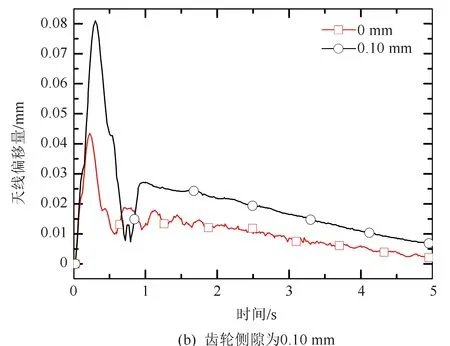
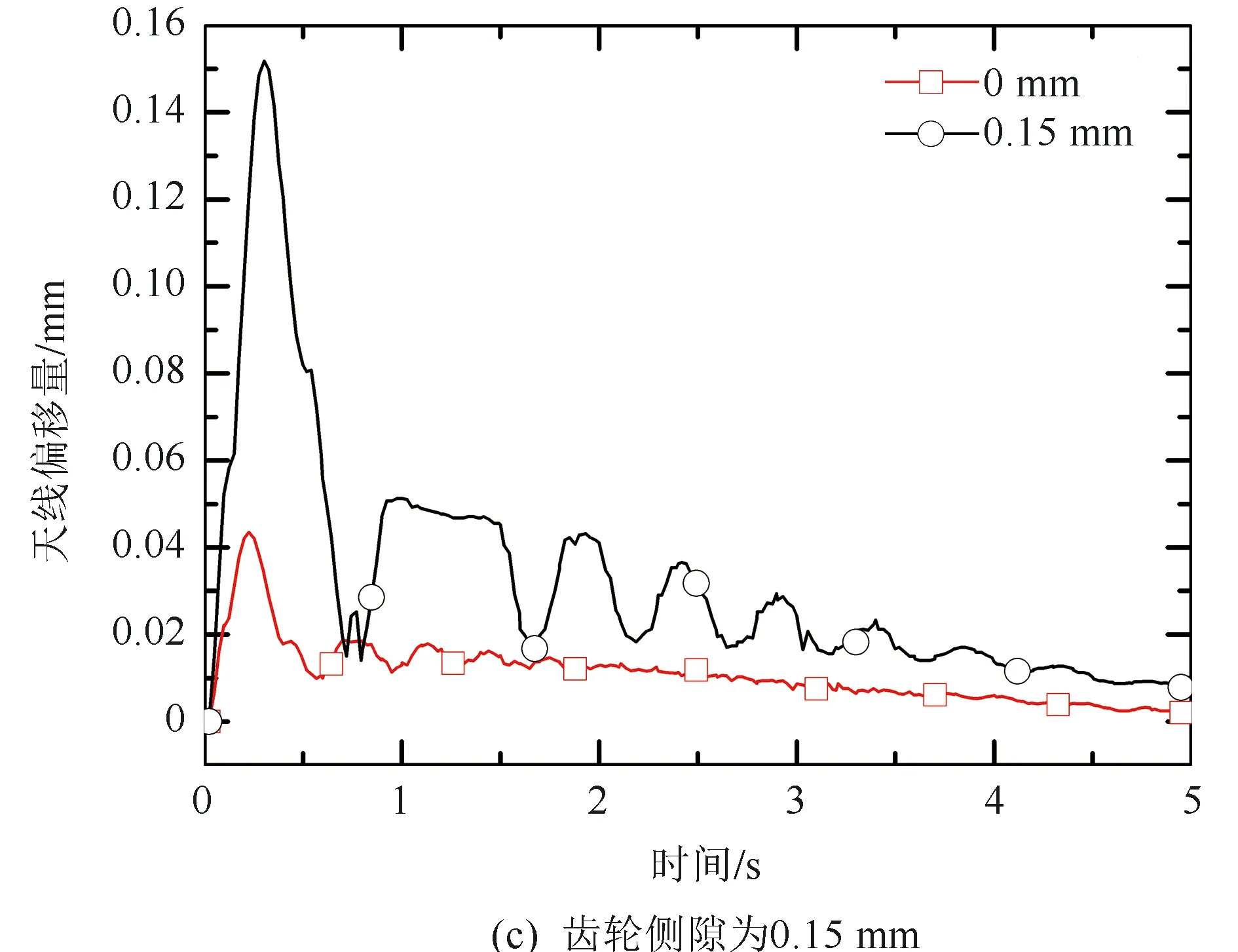
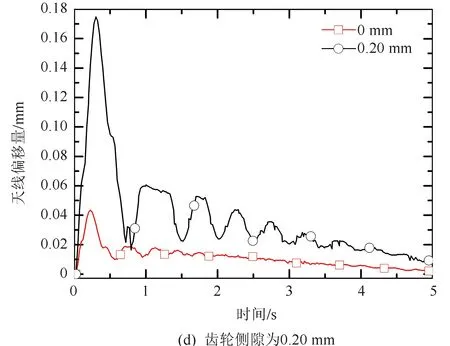
图5 不同间隙相对于理想状态下绝对偏移量

在一个行星轮系的基础上分析两个行星轮系对天线动力学的耦合影响，两个关节的行星轮系均采用相同的齿轮侧隙，对上述5种不同侧隙情况进行仿真分析。仿真时，转速为8.0(°)/s，仿真时长为5.0 s，摩擦系数为0.2。

仿真结果如图6所示，齿轮侧隙越小，天线相对偏移量的波动越小，但由于两个行星轮系关节的耦合作用，导致天线指向呈现更复杂的运动特性。相比于单行星轮系关节，双行星轮系关节系统中的多间隙运动过程中由于不同时处于接触或悬空状态，发生强烈的耦合作用，间隙的相互抵消或叠加导致关节间碰撞更加剧烈，使天线偏移量波动更加明显，频率更快，幅值更大，周期性不够明显，且波动时间更长，无法尽快恢复接触状态。由图6与图5对比可知，双行星轮系关节导致的天线偏移量在同等齿轮侧隙下约为单关节的两倍，间隙越大时，出现极限碰撞位置的频率越高，行星轮系的轮齿啮合精度明显下降，天线偏移量波动更大。因此，在设计时，应该尽量同时减小两个行星轮系齿轮侧隙，以提高行星轮系传动精度。

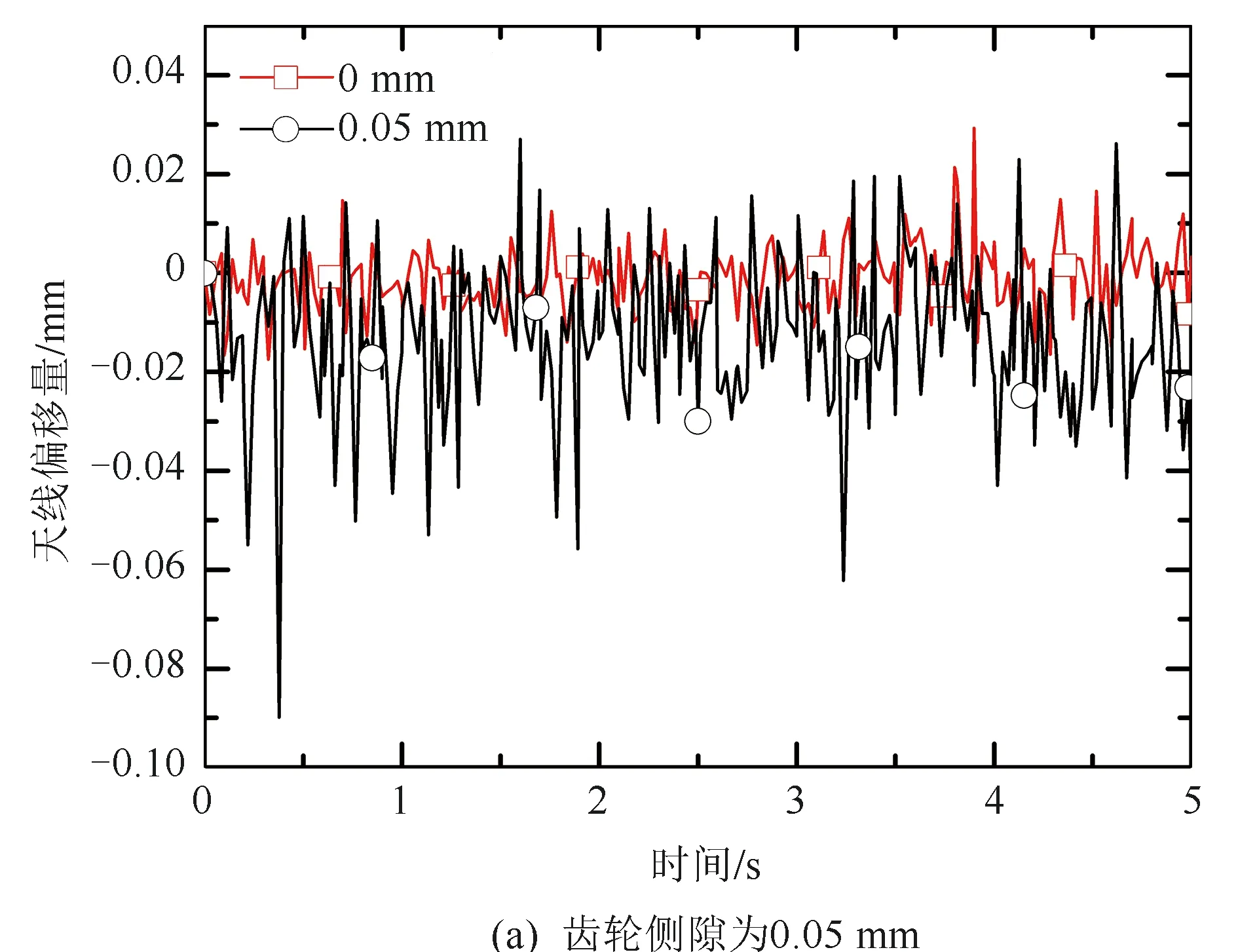
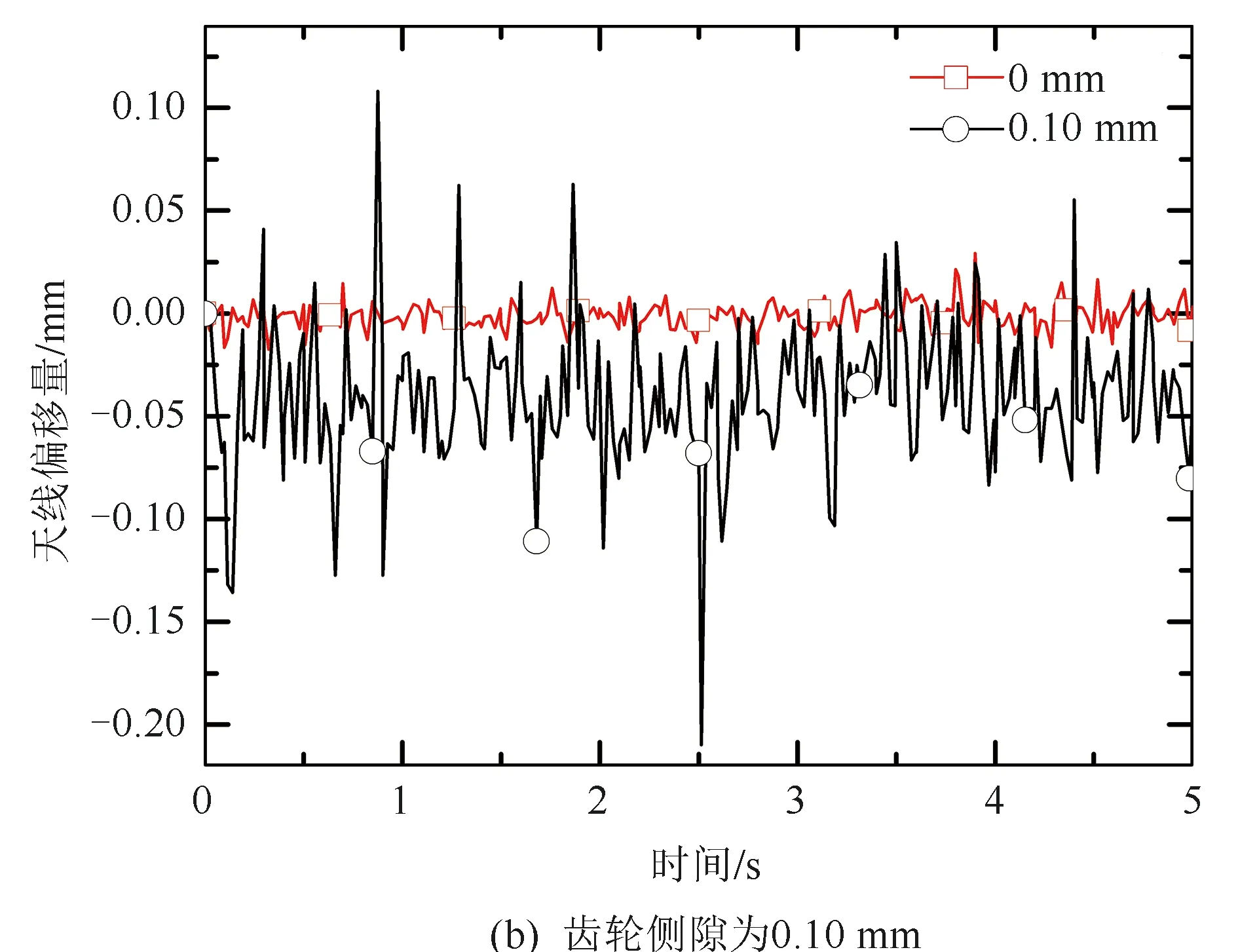
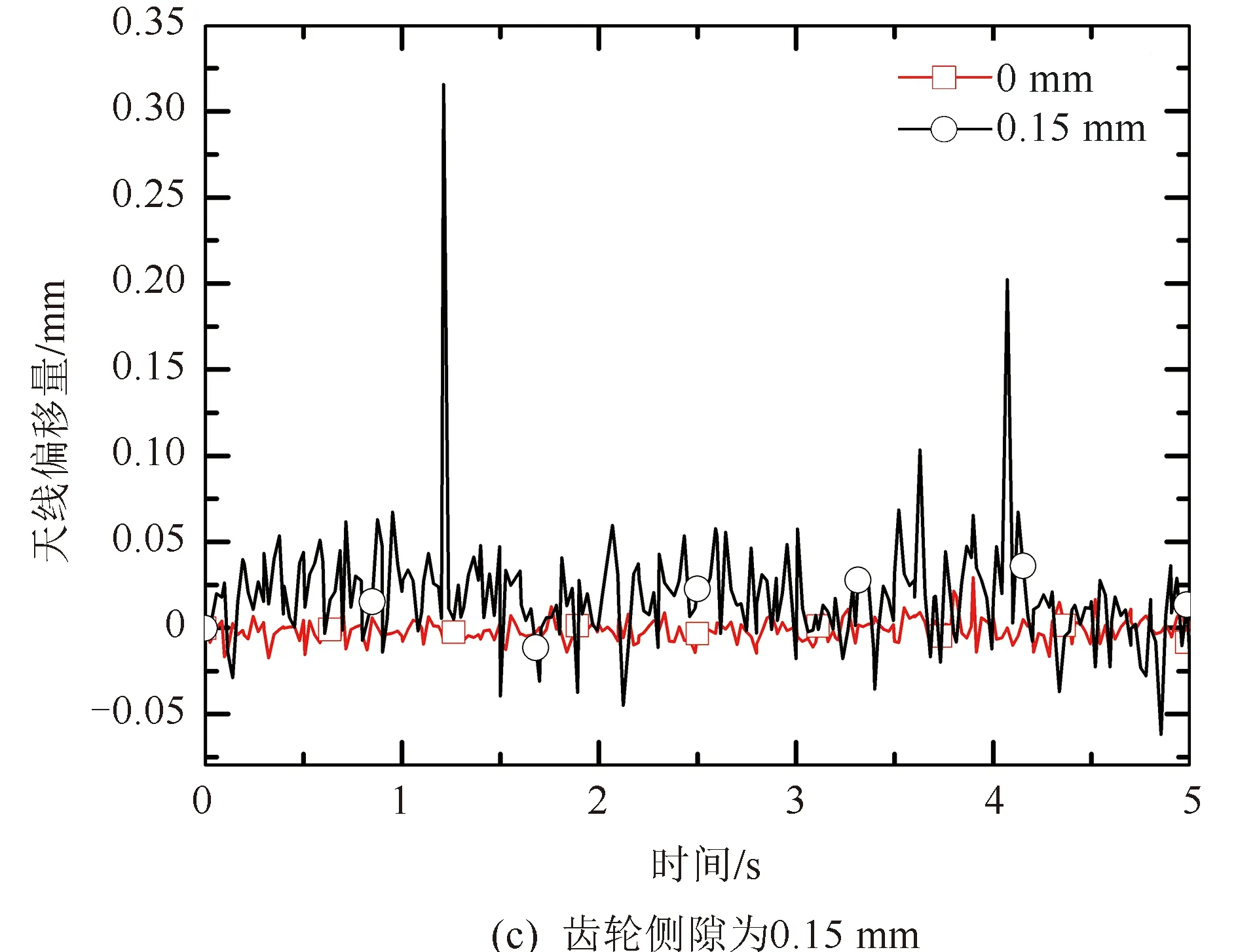
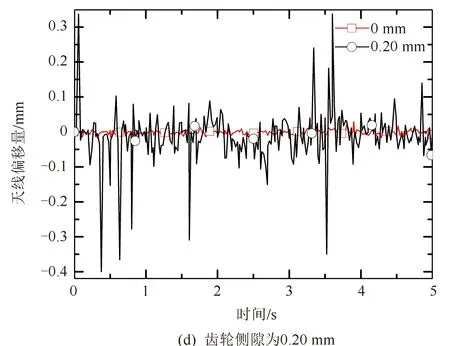
图6 不同间隙相对于理想状态下相对偏移量

4 结论

本文针对行星轮系关节存在齿轮侧隙因素对天线指向精度的影响，采用多体动力学方法构建了含齿轮侧隙行星轮系的天线系统动力学模型，通过Newmark数值方法，仿真分析了齿轮侧隙对天线指向精度的影响：

(1)在单个行星轮系关节中，当齿轮侧隙大于0.15 mm时，导致天线偏移量超过0.14 mm，且随着齿轮侧隙的增大，可能出现齿轮脱齿现象，造成更大的冲击，对天线的指向精度更为不利。

(2)相对于单行星轮系关节，双行星轮系关节中，由于存在耦合作用，天线偏移量波动频率更高，幅值更大，呈现更复杂的运动特性。当齿轮侧隙为0.15 mm时,所造成的天线偏移量绝对值达到了0.3 mm，尽可能减小齿轮侧隙能保证行星齿轮关节传动的稳定，在加工制造中，将齿轮侧隙控制在0.1 mm以下，有利于提高星载天线的指向精度。

References)

[1] 张锋，丁洪生，付铁，等. 星载天线指向机构误差分析与建模[J]. 电子机械工程，2010，26(1)：41-44

Zhang Feng，Ding Hongsheng，Fu Tie，et al. Analysis and modeling of pointing error for antenna pointing mechanism[J]. Electro-Mechanical Engineering，2010，26(1)：41-44 (in Chinese)

[2] 潘博，张东华，史文华，等. 星载天线指向精度建模与分析[J]. 航天器工程，2011，20(5)：49-54

Pan Bo，Zhang Donghua，Shi Wenhua，et al. Modeling and analysis on pointing accuracy of antenna in satellite[J]. Spacecraft Engineering，2011，20(5)：49-54 (in Chinese)

[3] 孙京，马兴瑞，于登云. 星载天线双轴定位机构指向精度分析[J]. 宇航学报，2007，28(3)：545-550

Sun Jing，Ma Xingrui，Yu Dengyun. Pointing accuracy analyses of a satellitic two-axes antenna pointing mechanism[J]. Journal of Astronautics，2007，28(3)：545-550 (in Chinese)

[4] 张慧博，陈军，潘冬，等. 含间隙卫星天线双轴驱动机构动力学特性分析[J]. 宇航学报，2012，33(1)：33-39

Zhang Huibo，Chen Jun，Pan Dong，et al. Research on dynamic characteristic of two-axis-position mechanism for satellite antenna with joint clearance[J]. Journal of Astronautics，2012，33(1)：33-39 (in Chinese)

[5] 游斌弟，潘冬，赵阳. 关节铰间隙对漂浮基星载天线扰动研究[J]. 宇航学报，2010，31(10)：2251-2258

You Bindi，Pan Dong，Zhao Yang. Research on disturbance of joints with clearance on free-floating satellite antenna[J]. Journal of Astronautics，2010，31(10)：2251-2258 (in Chinese)

[6] Salagianni K，Nikolakopoulos P，Theodossiades S. Dynamic and tribological study of a planetary gearbox with local nonlinearities[J]. Proceedings of The Institution of Mechanical Engineers Part K-Journal of Multi-Body Dynamics，2017,231(3)：504-518

[7] Spitas C, Spitas V. Coupled multi-DOF dynamic contact analysis model for the simulation of intermittent gear tooth contacts, impacts and rattling considering backlash and variable torque[J]. Archive Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science，2015，230(7)：1989-1996

[8] Al-Shyyab A，Kahraman A. A non-linear dynamic model for planetary gear sets[J]. Proceedings of the Institution of Mechanical Engineers Part K Journal of Multi-body Dynamics，2007，221(4)：567-576

[9] 李同杰，朱如鹏，鲍和云，等. 行星齿轮系扭转非线性振动建模与运动分岔特性研究[J]. 机械工程学报，2011，47(21)：76-83

Li Tongjie，Zhu Rupeng，Bao Heyun，et al. Nonlinear torsional vibration modeling and bifurcation characteristic study of a planetary gear train[J]. Journal of Mechanical Engineering，2011，47(21)：76-83 (in Chinese)

[10] 周璐，巫世晶，李景，等. 2K-H行星轮系的平移扭转模型建立与非线性动态特性分析[J]. 振动与冲击，2016，35(12)：71-76

Zhou Lu，Wu Shijing，Li Jing，et al. Establishment of translational and torsional model and nonlinear dynamic characteristic analysis for 2K-H planetary gear trains[J]. Journal of Vibration And Shock，2016，35(12)：71-76 (in Chinese)

[11] 孙涛，沈允文，孙智民，等. 行星齿轮传动非线性动力学方程求解与动态特性分析[J]. 机械工程学报，2002，38(3)：11-15

Sun Tao，Shen Yunwen，Sun Zhimin，et al. Study on nonlinear dynamic behavior of planetary gear train solution and dynamic behavior analysis[J]. Journal of Mechanical Engineering，2002，38(3)：11-15 (in Chinese)

[12] 孙智民，季林红，沈允文. 2K-H行星齿轮传动非线性动力学[J]. 清华大学学报(自然科学版)，2003，43(5)：636-639

Sun Zhimin，Ji Linhong，Shen Yunwen. Nonlinear dynamics of 2K-H planetary gear train[J]. J Tsinghua Univ ( Sci & Tech)，2003，43(5)：636-639 (in Chinese)