考虑拖期风险的第四方物流路径优化问题模型与求解
,
(1.辽宁石油化工大学 a.信息与控制工程学院 b.石油化工过程控制国家级实验教学示范中心,辽宁 抚顺 113001;3.东北大学信息科学与工程学院流程工业综合自动化国家重点实验室,沈阳 110819)
0 引言
第四方物流(The Fourth Party Logistics,4PL)供应商是一个供应链的集成商,它对公司内部和具有互补性的服务供应商所拥有的不同资源、能力和技术进行整合和管理,以提供一整套供应链解决方案。4PL的发展一方面给物流企业发展带来了机遇,另一方面,也给理论界带来许多具有挑战性的研究问题,如4PL的运行优化[1-2]、利润分配[3]、网络设计[4-5]、路径优化[6]等等。
4PL路径优化问题(4PL Routing Optimization Problem,4PLROP)是在复杂物流配送网络中寻求供应城市到需求城市的一个配送路径,4PL供应商在选择路径的同时还要对提供配送服务的第三方物流(The Third Party Logistics,3PL)供应商做出选择。因此,增加了问题的求解难度。但它是4PL运作优化的关键问题之一,已经成为国内外理论界和企业界特别关注的焦点。目前,已有许多研究学者对4PLROP展开研究,并取得一些成果,为4PLROP问题的研究奠定了基础。Chen等[7]从4PL运作的关键问题出发,基于图论知识建立了4PLROP的多维权有向图模型,采用遗传算法求解了10节点的4PLROP问题。考虑到Chen给出的是4PLROP的概念模型,Huang等[8]基于配送网络的多重图,给出了4PLROP的具体的数学模型,并设计嵌入Dijkstra算法的免疫算法对该模型进行了求解。继而,基于免疫规划对免疫算法进行了改进,对该问题进行了进一步的求解,并与传统的免疫算法进行了对比分析[9]。考虑到客户对交货期的需求可能具有时间窗特征,Bo等[10]建立了带时间窗的4PLROP数学模型,并利用和声搜索算法对该问题进行了求解。在此基础上,作者进一步对时间窗的硬约束进行释放,即考虑了带软时间窗的4PLROP,对不满足时间窗要求的路径进行相应惩罚,并加到目标函数中[11]。考虑到多任务的情况,黄[12]等建立了带有费用折扣的4PLROP模型,并采用蚁群算法对问题进行求解。Tao[6]等采用列生成算法对所建立的模型进行了求解。在物流配送过程中,配送时间往往受天气、路况等其他因素的干扰,导致不能按期完成配送任务,从而带来不确定性。为了提高服务水平,需要对配送时间的不确定性进行有效的刻画。Huang等将这种不确定性看成是模糊的,建立了相应的模糊规划数学模型,并分别用遗传算法[13]、两阶段遗传算法对相应的数学模型进行了求解[14]。Huang等[15]将配送时间看成是不确定的,采用不确定性理论建立了不确定性模型,并将其转化成确定性模型,采用改进的不同的遗传算法对问题求解。Huang等在文[16]中又将不确定模型与随机规划模型进行了对比分析,论证了不确定性模型的有效性。
但当前研究没有对由于时间的不确定性而引起的风险进行刻画、度量与控制。在实际的配送过程中,正是由于在4PL运作中3PL供应商的运输时间和中转时间存在着不确定性,导致配送任务不能按期完工,从而带来拖期风险。使得4PL供应商不能为客户提供及时优秀的配送方案,而导致配送成本的增加及自身信誉和客户满意度的下降。因此,研究考虑拖期风险的4PLROP问题具有理论和实际意义。
本文在充分考虑上述实际情况下,引入了在险值(Value-at-Risk,VaR)来刻画及度量拖期风险的大小,即拖期量小于某个值的概率要大于给定的置信水平。建立了以最小化拖期风险为目标,配送费用为约束的数学模型,并设计具有复杂网络搜索能力的嵌入删除算法的和声搜索算法(Deletion Algorithm Embedded Harmony Search,DA-HS)对问题进行求解,测试了不同规模的实例,并将求解结果与嵌入删除算法的遗传算法(Deletion Algorithm Embedded Genetic Algorithm,DA-GA)、基本的声搜索算法(Harmony Search,HS)和枚举算法(Enumeration Algorithm,EA)进行了对比分析,测试结果表明所提模型和算法是有效的。
1 数学模型
1.1 问题描述及变量定义

图1 7节点问题的多重图Fig.1 Multi-graph of seven nodes problem
如图1所示,4PLROP可以用多重图G(V,E)进行表示,其中V(V=n)表示节点的集合,E表示边的集合。s是供应城市,t是需求城市,其他中间点是中转城市,它们具有费用和时间属性。假设每段运输任务只能由一个3PL供应商负责,由于任意两个城市之间可能存在多个3PL提供配送服务,故图中任意两点间可能有多条边(每条边代表一个3PL,边上的数字是3PL的编号),每条边都具有费用和时间属性。
供应商为客户提供配送方案时,要考虑到时间的不确定性而导致的拖期风险,对风险进行度量及监控,以满足客户对配送时间的需求,提高客户的满意度。对客户来说,只要费用在其预算之内,按时完工的概率越大越好;一旦拖期的话,拖期量越小越好,即最大程度地保证按时完成配送任务,一旦拖期,拖期风险越小越好。因此,基于以上考虑,在用VaR来度量拖期风险的基础上,建立以最小化拖期风险为目标,配送费用为约束的数学模型。目标是求得满足费用约束的拖期风险最小的配送的方案。
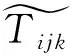
(1)
(2)
1.2 VaR的定义
VaR的比较规范的定义是,在正常的市场条件和给定的置信水平上,在给定的持有期间内,某一投资组合预期可能发生的最大的损失。或者说,在正常的市场条件和给定的时间段内,该投资组合发生大于VaR值损失的概率仅为给定的概率水平,可以表示为
Pr{ΔP>VaR}=1-β
(3)
其中,ΔP为证券组合在持有期内的损失,β为置信水平,VaR为置信水平β下处于风险中的价值。置信水平的选取反映了投资主体对风险的厌恶程度,置信水平越高,厌恶风险的程度越大。由VaR的定义可知,置信水平越高,资产组合的损失小于其VaR值的概率越大,也就是说,VaR模型对于极端事件的发生进行预测时失败的可能性越小。

图2 VaR的定义Fig.2 Definition of VaR
如果Z是随机变量,则VaR的数学定义如式(4)[17],其中,β是置信水平。图2给出了VaR定义的图示。例如,某公司1994年年报披露,1994年该公司一天的95%VaR值为100万美元。其含义是指,该公司可以以95%的可能性保证,1994年每一特定时点上的证券组合在未来24小时之内,由于市场价格变动而带来的损失不会超过100万美元,即损失超过100万美元的概率不会超过5%。
VaR(Z)=inf{t:p(z≤t)≥β}
(4)
本文中采用VaR来度量拖期风险的大小,即拖期量小于某个值的概率要大于等于客户给定的置信水平。
1.3 VaR准则下的数学模型
基于以上变量定义,建立如下数学模型:
minVaRβ(ΔT)
(5)
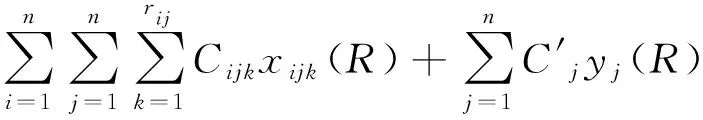
(6)

(7)
R={vs,…,vi,k,vj,…,vk}∈G
(8)
xijk(R),yj(R)∈{0,1}
(9)
式(5)是目标函数,最小化拖期风险,即VaR值,β为置信水平,即客户的风险偏好;式(6)是配送费用约束,其中C0是客户给定的可提供的最大的费用;式(7)是随机变量,即拖期量ΔT的表达式;式(8)是路径约束,即保证所选路径是从初始点到目的点的合法的连通路径;式(9)是决策变量约束。
1.4 VaR的转化
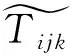

(10)
2 算法设计
文献[10]设计了HS算法来求解4PL路径优化问题,但是该算法不能保证所产生的初始解和新解是合法解(合法的路径),因此需要对非法解进行修复。修复过程会丢失当前解的优良信息,且当问题规模比较大的时候,此修复过程非常耗时。从而导致该算法在求解大规模问题时,不能在合理的时间内找到最优解或满意解。
因此,针对上述问题及4PL路径优化问题的特点,设计了DA-HS算法。主要设计思想是:先在多重图上用HS算法的优化机制产生一个简单图;然后用DA算法在此简单图上求出前K条拖期风险最小的路径。由于最优解不一定是某个图上的最短路径,也有可能是次最短路径,因此该算法求前K条最短路径而不是最短路径。该算法每次迭代能产生多个解,而传统的HS算法仅产生一个解,提高了算法的收敛速度。
本节先简单介绍HS和DA算法,然后介绍本文提出的DA-HS算法以及DA-GA算法。
2.1 和声搜索算法
HS算法是2001年韩国学者Geem等人通过类比音乐和最优化问题的相似性而提出的一种新的智能优化算法[19]。类似于遗传算法对生物进化的模仿、模拟退火算法对物理退火机制的模仿以及粒子群优化算法对鸟群鱼群的模仿等,HS模拟了音乐演奏的原理。音乐演奏中,乐师们凭借自己的记忆,通过反复调整乐队中各乐器的音调,最终达到一个美妙的和声。算法首先产生HMS(Harmony Memory Size,和声记忆库的大小)个初始解(和声)存入和声记忆库(Harmony Memory, HM)中;每个设计变量以概率HMCR(Harmony Memory Considering Rate,HMCR)在HM内搜索新值,以概率1-HMCR在变量可能值域中搜索新值;对于在HM中产生新值的设计变量,以概率PAR(pitch adjusting rate,PAR)产生局部扰动;判断新解目标函数值是否优于HM内的最差解,若是,则替换之;然后不断迭代至收敛。
2.2 删除算法
删除算法(Deletion Algorithm,DA)[20]的核心思想:通过在有向图中已有的最短路径上删除某条弧,并寻找替换的弧来寻找下一条可选的最短路径。DA算法实际上是通过在有向图中增加附加节点和相应的弧来实现的。算法的详细步骤可参考文献[16]。
2.3 嵌入删除算法的和声搜索算法
该算法主要包括编码设计、初始化问题和算法参数、初始化HM、新解的产生、更新HM、终止准则。
2.3.1 编码方案
采用以边为基础的整数编码。先将多重图用邻接矩阵表示,矩阵中的行和列分别代表多重图上的节点,图中有边相连的两节点对应的矩阵元素值为两节点间的边数,即rij;没有边相连时对应的矩阵元素值为0。然后将矩阵中的上三角非零元素逐行从左到右编码得到一个向量n=(n1n2…ni…nN),其中ni为第i个解分量hi的最大取值,N为该问题的编码长度,即解分量的个数。当表示简单图的时候,每个解分量取值为1≤hi≤ni,当表示路径的时候,每个解分量hi可以取零值。
以图1为例,其邻接矩阵如(11)所示,可得7节点问题的向量n=(3 4 2 2 2 3 4 3 2 3 2 2)。由此可知,7节点问题解分量为12个,每个解分量的最大取值分别为3,4,2,2,2,3,4,3,2,3,2,2。图3给出了向量h=(3 2 3 1 1 1 2 2 2 1 2 1)所代表的简单图,简单图上求得的最短路径h=(3 0 0 1 0 0 0 0 0 1 0 0)如图3中粗线所示。

图3 简单图及图上的最短路径Fig.3 A simple graph and the shortest path in it
(11)
2.3.2 初始化问题和算法参数
初始化问题的参数:和声记忆库的大小HMS、和声记忆保留概率HMCR、记忆扰动概率PAR、最大迭代次数NG、参数K、置信水平β、客户可提供的最大的费用C0和客户要求的配送时间T0。
2.3.3 初始化HM
主要思想:对每个解分量hi随机选取1~ni之间的一个整数,即随机产生一个简单图,然后在此图上用DA求出前K条拖期风险最小的路径。将满足费用约束的解(即路径)存入HM中,不满足费用约束的解放弃,直到产生HMS个初始解,并按目标函数值对初始解排序。其中,HMS与K没有倍数关系。
(12)
DA-HS算法中的HM与HS算法的记忆库有所不同。该算法的HM如矩阵所示,HM分为3部分,第1部分存放简单图,第2部分存放在简单图上求得的路径,第3部分是目标函数,即该路径的拖期风险的大小。
以7节点问题为例,假定HMS=3,K=3。先随机产生一个简单图h=(3 2 3 1 1 1 2 2 2 1 2 1),如图3所示;然后,用DA求出前3条最短路,并存入HM,如式所示。

2.3.4 产生新解
主要思想:先用HS优化机制产生新的简单图,然后调用DA求出前K条拖期风险最小的路径。
由于HS算法的优化机制用来产生新的简单图,此时的每个解分量hi不能取零值。为了产生新的简单图,现对每个解分量hi进行如下操作:
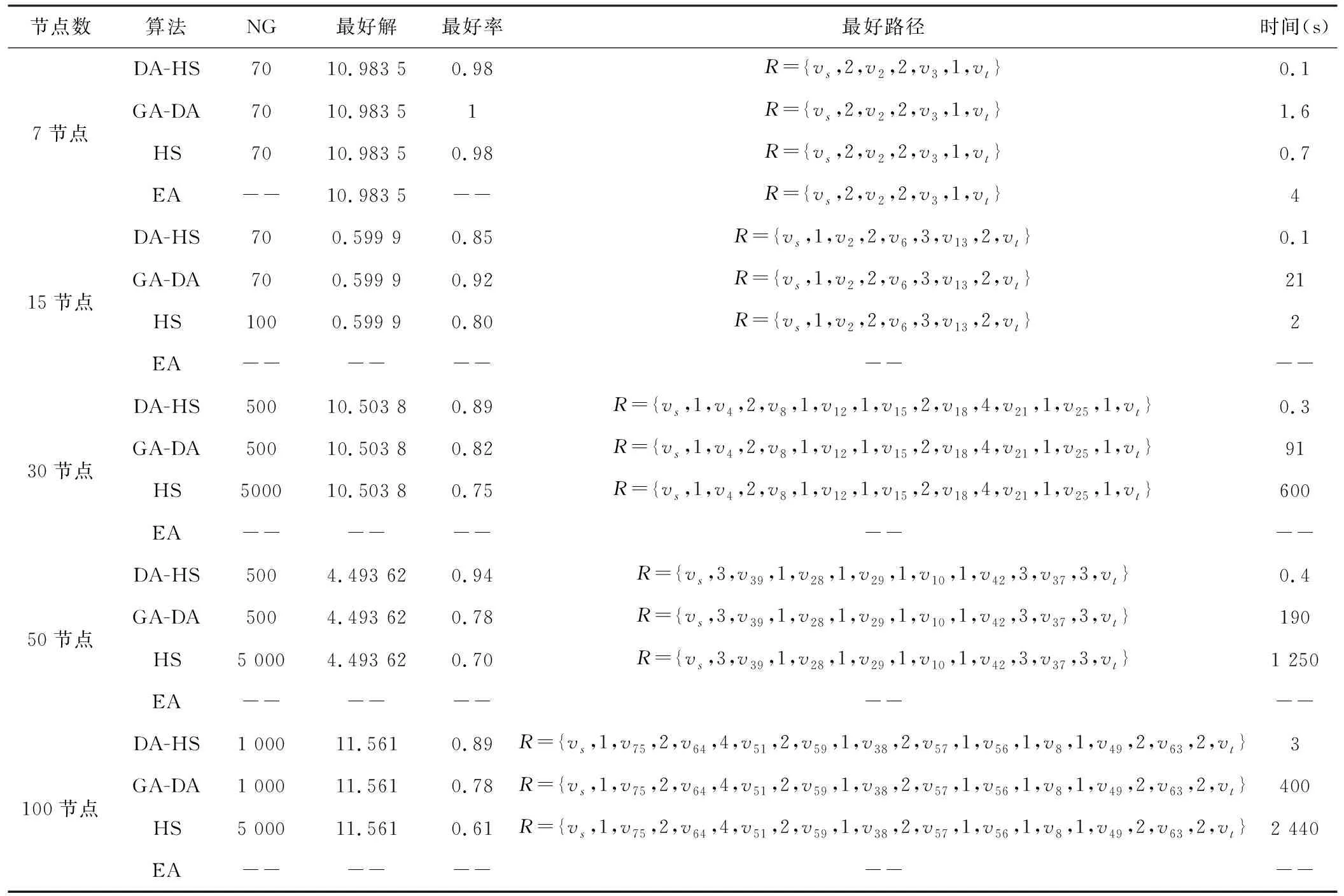
1)生成随机数r1∈(0,1),如果r1 2)生成随机数r2∈(0,1),如果r2 2.3.5 更新HM 对新产生的K个新解依次做如下操作: 1)新解是否满足费用约束,若是转下步;否则转3)。 2)新解是否比HM中的最差解要好,若是则用新解替换最差解;否则转下步。 3)K个新解是否都判断完,若是则更新HM完毕并对HM中所有解排序;否则转(1)进行下一个新解的判断。 4)终止准则 如果迭代次数达到NG,则算法终止,输出最好解;否则,转4)重新产生新解。 2.3.6 算法步骤 步骤1:初始化算法的参数:HMS、HMCR、PAR、NG、K、置信水平β、C0和T0。 步骤2:初始化HM。对HM中所有解(HMS个)按目标函数进行排序。 步骤3:产生新解。用HS算法的优化机制生成新的简单图,然后调用DA算法求出前K条目标函数值最小的路径。 步骤4:更新HM。 步骤5:如果迭代次数达到NG,则算法结束并输出最好解;否则转步骤 3。 编码方案和初始种群的产生方法同DA-HS算法。目标函数作为适值函数,即最小化拖期风险。选择策略采用截断选择方法,选择最好的前T个个体,让每一个个体有1/T的选择概率,即平均每个得到NP/T个繁殖机会[21]。交叉方式为单点交叉。最大迭代次数作为停止准则。 产生新一代种群的主要思想:先用GA优化机制产生新的简单图,然后调用DA求出前K条拖期风险最小的路径。 为了验证上述问题的数学模型和算法的有效性,本节测试了5个不同规模的算例,并将测试结果与DA-GA、HS[11]和EA进行了对比。算法采用VC++语言实现,运行环境为Intel(R)Core(TM)i7-2600CPU 3.40GHz PC台式机。 本节分别求解了7,15,30,50和100节点的5个不同规模的算例。其中,其中7,15和30节点的数据来自文献[10];50和100节点问题的数据是随机产生的,随机产生数据方法为:将n个节点随机地放在一个a*a的正方形区域内,点(0,0)和(a,a)分别代表初始节点和目的节点,如果两个节点间的欧几里得距离小于等于d,则两节点间有边相连[22],有边相连的节点间边的个数在闭区间[2,4]中随机生成,边的费用和时间、节点的费用和时间都是随机生成的。50节点算例的网络节点分布图,其中a=3,d=0.75;100节点算例的网络节点分布图,其中a=4,d=0.7。 图4 参数NG性能分析Fig.4 w. r. t. NG performance analysis 以7节点问题为例,详细测试了算法参数对算法性能的影响并获得一组最佳参数组合。算法参数的获取是经过大量仿真实验获得的,即当其他参数不变时,测试某一个参数对算法最好率的影响。图4给出了NG对算法性能的影响,由图可知,当NG达到70以后,算法趋于稳定。其中,最好率为算法获得最好解的次数占算法运行总次数的比率,计算最好率时算法运行总次数为100。仿真实验表明,DA-HS算法最好的参数分别为K=2,HMS=5,HMCR=0.75,PAR=0.05,NG=70。 本节首先以7节点问题为例,详细分析了算法的求解结果。其次,为了验证算法的有效性,分别求解了7,15,30,50和100节点的5个不同规模的算例,将3种算法的求解结果进行了对比分析。 表1给出了当时间约束T0=80和费用约束C0=73时,7节点问题的求解结果。 表1 T0=80,C0=73时7节点问题算法的求解结果Tab.1 Results of algorithm for solving 7 nodes problem with T0=80, C0=73 由表中数据可知,当置信水平β=0.9时,求得的最好解(VaR值)为10.983 5,即物流供应商以90%的概率能够保证配送时间的拖期量小于等于10.983 5,对应的配送费用为73,对应的配送路径为R={vs,2,v2,2,v3,1,vt},即在供应城市s和需求城市t间选择编号为2和3的城市作为中转城市,两两城市间提供配送服务的3PL编号分别为2,2,1;当置信水平增加到β=0.95时求得的最好解(VaR值)为19.473 3,即以95%的概率能够保证配送时间的拖期量小于等于19.473 3,对应的配送费用为73,对应的配送路径为R={vs,2,v2,2,v3,1,vt},即在供应城市s和需求城市t间选择编号为2和3的城市作为中转城市,两两城市间提供配送服务的3PL编号分别为2,2,1;当置信水平增加到β=0.99时,求得的最好解(VaR值)为35.400 6,即拖期量超过35.400 6的概率小于1%,对应的配送费用为73,对应的配送路径为R={vs,2,v2,2,v3,1,vt},即在供应城市s和需求城市t间选择编号为2和3的城市作为中转城市,两两城市间提供配送服务的3PL编号分别为2,2,1。上述结果表明,当时间约束和费用约束不变时,随着置信水平的增加(风险厌恶),配送路径不变,但是拖期量增大。因此,4PL可以根据客户的风险偏好,控制拖期量的大小,在风险和拖期量之间做个权衡。 表2给出了置信水平、配送时间和费用约束的不同组合下,7节点问题的求解结果。其中,“β”为置信水平;“T0”为客户要求的最晚的配送时间;“C0”为客户给定的可承担的最大费用值;“NG”是算法的迭代次数;“最好解”是算法能够求得的最好的解(评价标准是目标函数);“最好率”为算法运行100次中找到的最好解的个数与100的比率;“最好路径”是最好解对应的配送路径;“时间”是算法运行一次的运行时间,单位秒。 表2 不同β、T0和C0下7节点问题的求解结果Tab.2 Results of 7 node case with different value ofβ, T0and C0 由表2中数据可知,当置信水平β和配送时间T0不变时,随着费用的增加,拖期风险逐渐减小;当置信水平β和配送费用C0不变时,随着可允许的配送时间的延长,拖期风险越来越小;当配送时间T0和配送费用C0不变时,随着置信水平β的增加,拖期风险越来越大。4PL供应商可以根据客户不同的风险偏好、时间和成本需求选择合适的配送方案以控制风险。 为了更好地测试DA-HS算法的性能,将算法求解不同实例的结果与DA-GA、HS和EA进行了对比分析。表3给出了当客户的置信水平β=0.9时,相同配送时间和配送费用约束下,4种算法求解5个实例的结果对比。“--”表示EA不能在有限时间内得到可行解。其中,15节点的时间和费用约束分别为70和115;30节点的时间和费用约束分别为115和190;50节点的时间和费用约束分别为150和165;100节点的时间和费用约束分别为210和260。 表3 4种算法求解不同规模问题的结果对比Tab.3 Comparison of four algorithms for different size 由表3中数据可知,本文设计的算法能够很快地求解不同规模的实例且解的质量很好。对于7节点问题,DA-HS、DA-GA、和HS能快速地获得和EA一样的最优解。对于中等及以上规模的问题,EA不能在有效时间内得到最优解,而其他3种智能计算方法均可以得到相同的最好结果。但是随着问题规模的增大HS求解时间增加的很快,而最好率却逐渐下降,究其原因,HS将大量的时间浪费在不合法解的修复上;DA-HS和DA-GA、避免了解的修复环节,因此节省了大量的计算时间用来获得更高质量的解。对于100节点的问题,DA-HS仍能快速获得最好结果,且有较高的最好率,且最好率及求解时间较DA-GA更好,充分说明了DA-HS具有较高水平的求解速度和质量。本文设计的算法是求解带有拖期风险的4PLROP问题行之有效的方法。 本文充分考虑现实复杂物流配送过程运输时间和中转时间的不确定性而导致配送任务不能按时完工的情况,在引入了在险值(VaR)来量化拖期风险大小的基础上,对4PL路径优化问题展开研究。建立以最小化拖期风险为目标,费用为约束的数学模型,并设计了DA-HS算法对问题进行求解。通过对不同实例的求解结果进行分析表明,该算法能够快速地求解大规模问题,且算法具有很好的稳定性,优于DA-GA、HS和EA。为考虑拖期风险的4PL路径优化问题提供了可供参考的数学模型及有效的求解算法,4PL供应商可以根据客户的风险偏好和预算来决策可行的配送方案。2.4 嵌入删除算法的遗传算法(DA-GA)
3 实例分析
3.1 数据的产生

3.2 参数测试
3.3 算例分析


4 结论

