基于多元线性回归方法的高校宿舍建筑能耗分析

孙 晴，李明海，鲁 娟，刘 敏

(1.西安建筑科技大学 建筑设计研究院，陕西 西安 710055 ；2. 西安建筑科技大学 信控学院，陕西 西安 710055;3.安徽农业大学 总务处，安徽 合肥，230036)

近年来，随着高校办学规模的不断扩大，高校宿舍的数量逐年攀升.截止2013年，全国高校累计2788所，在校生达3460万人，高校能耗是我国各类建筑能耗大户，有数据表明目前我国高校单位建筑面积能耗高于全国居民单位面积能耗[1].因此，针对高校宿舍进行节能研究，可为国家实施高等学校节约型校园建设工作提供指导意见[2].

在高校宿舍类建筑节能研究方面，樊丽军以电力和天然气为能耗目标值，将居住人数、建筑年代及类型等参数为输入变量，提出了建筑节能和建筑能耗预测的多元线性回归分析模型[3]；王琳对重庆地区高校宿舍进行了连续的物理参数测试，得出夏季学生可接受的温湿度范围[4]；张玲等基于上门访问问卷调查法和多元统计分析法，探寻了上海地区某高校学生宿舍高能耗的源头[5]；Yufeng Zhang等分析了夏热冬暖地区安装分体式空调的高校宿舍的热舒适，发现热感觉为中性时人可接受的温度范围[6].国内外学者基于多元线性回归理论针对高校宿舍能耗影响因素的研究相对较少，而对高校宿舍热环境研究居多.同时，由于我国北方地区冬季为集中供暖地区，供暖能耗计量按照大单位统一设表计量，而宿舍供暖费用参照建筑面积一次性缴纳，客观上属不可控因素，故本次研究中未考虑供暖能耗因素的影响.因而，本文拟采用多元线性回归的方法，以西安市某高校宿舍施工图纸为工程背景，探索高校宿舍节能的潜在相关因素.

1 多元线性回归的基本理论

多元线性回归是反应多个因素对同一结果的影响，它是一种数理统计的方法[7].设反应变量为y，解释变量为x，a个解释变量的向量表达式为(x1，x2，…，xa)，设有n组观测值，第i组的观测值可表示为(xi1，xi2，…，xia，yi)，其多元线性回归的表达式为(1)式：

yi=c0+c1xi1+c2xi2+…+caxia+εi(1)

用矩阵形式表达，可简化为：y=xc+ε(c为多元线性回归方程的系数，ε为残差)，其中：

使用多元线性回归方法进行统计分析时，应满足如下四点条件[8-9]：

(1)解释变量与反应变量存在线性关系，可以通过绘制散点图来考察；

(2)残差满足正态性，可以采用残差的直方图或累计概率图验证；

(3)残差的协方差为0，可以通过Durbin-Watson检验说明；

残差的方差都是相等的，即残差满足方差齐次性，一般通过绘制预测值与残差间的散点图考察.

2 DeST宿舍模型的建立

2.1 工程背景

建筑能耗模拟的软件很多，常见如eQuest，EnergyPlus，DeST等.DeST软件含有丰富的作息时间库，可以针对不同房间的功能设置相应的热扰，软件掌握相对容易，同时DeST基于分阶段模拟的理念，它致力于辅助建筑环境及系统设计，以最小的能源代价来满足人们的热舒适性要求，主要应用于建筑及空调系统辅助设计、建筑节能评估等诸多领域[10].

本研究以西安某高校的六层宿舍施工图纸为背景，该宿舍建筑面积：19 744.38 m2，层高：3.6 m，建筑朝向：坐北朝南，其各层功能为：一层包括标准8人宿舍26间，强弱电井各1间，管理员办公室1间，公用卫生间1间，沐浴室1间，其余为走廊部分；二层将管理员办公室改为洗衣房，其它功能与一层相同；三至六层与二层相同.

本实验以配置为AMD双核A4-3305M APU、3GB DDR3内存的星锐4560G计算机为实验平台，考虑到DeST建模复杂、分阶段模拟时间较长，特将六层宿舍模型简化为两层宿舍简易模型，DeST建模结果如图1、图2所示：

图2 二层平面图Fig.2 Second floor of dormition plan

2.2 参数设置

DeST宿舍楼模型的基本参数如表1所示：

根据实际的作息时间表，分别设置楼梯、卫生间、宿舍、办公室、沐浴室、洗衣房的窗帘作息时间、相应位置门的开启时间、通风时间(由于西安高校宿舍基本未装空调，通风形式为自然通风)、各房间的热扰(如人员热扰、灯光热扰、设备热扰等)等参数，由于篇幅有限，该部分的参数繁琐，不一一列举.在建模阶段，每完成一部，将对已建的模型建筑预处理一次，避免了DeST建模时有些地方不符合系统内部的设置，提高了建模效率.

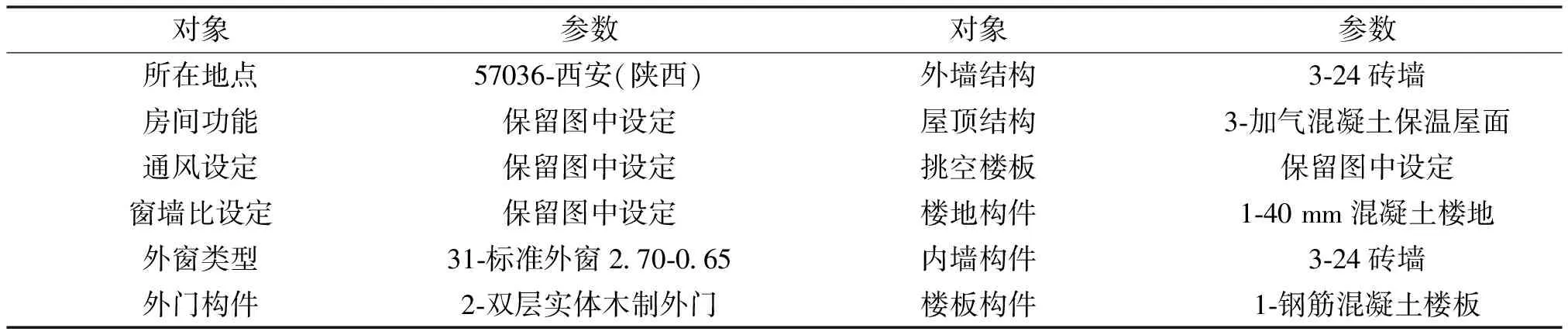
表1 宿舍模型的基本参数

2.3 模拟结果

建模完成后，进行系统仿真实验，可得到西安市全年8 760个逐时的气象参数(如干球温度、含湿量、总辐射)、建筑总能耗、照明电耗、设备电耗、给排水电耗等数据，现从中提取2016年1月1日24小时的数据如表2.

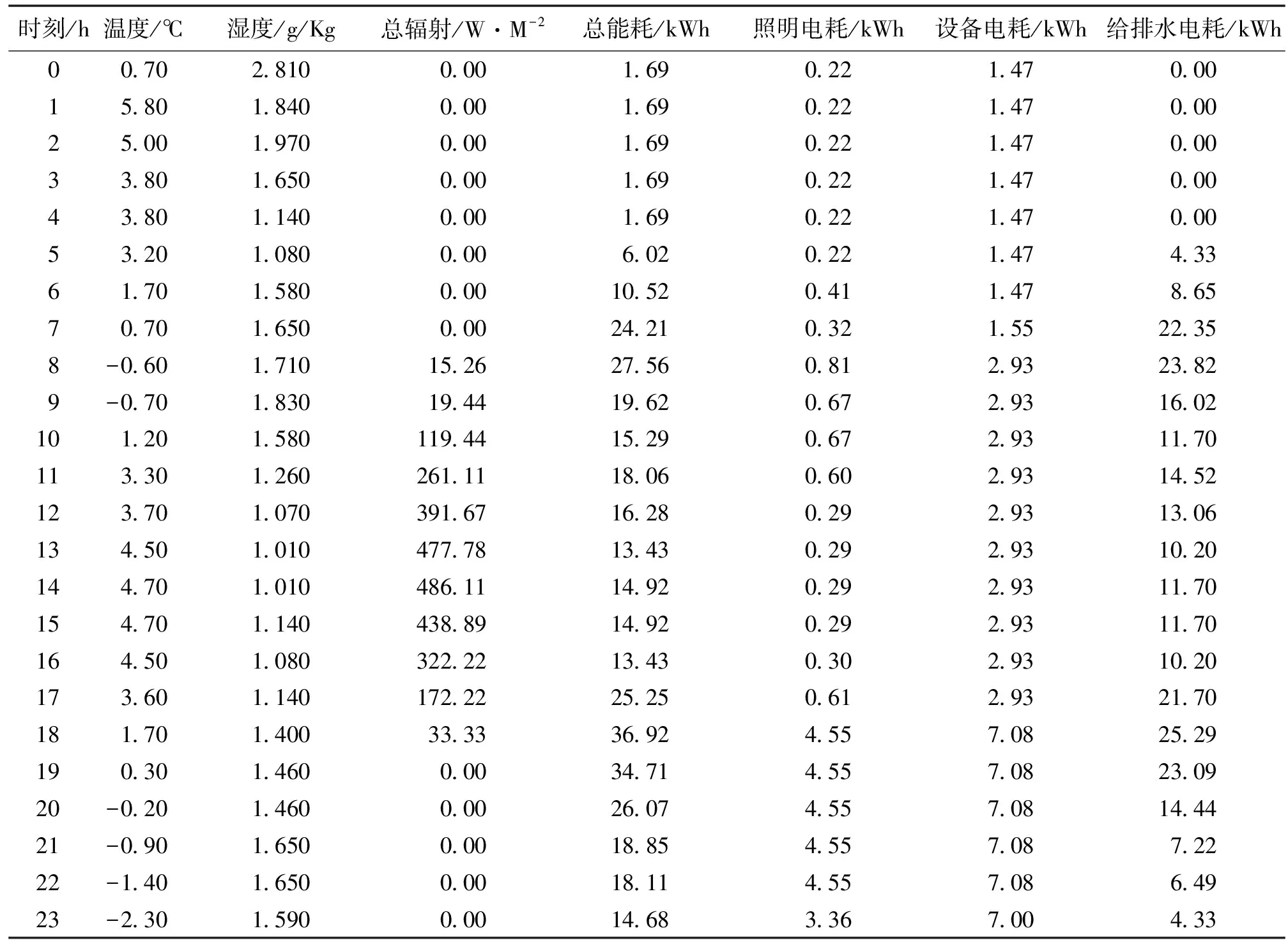
表2 宿舍模型模拟的部分结果

3 SPSS 22软件对实验数据的统计分析

SPSS即社会科学统计程序，是当今世界上最为流行的三大统计分析软件之一，是公认的最优秀的统计分析软件包，它的功能十分强大，在诸多领域得到广泛应用[9].本文采用SPSS 22高级版本对DeST宿舍楼模拟结果的七大参数即温度(x1)、湿度(x2)、总辐射(x3)、建筑总能耗(y)、照明电耗(x4)、设备电耗(x5)、给排水电耗(x6)全年的8 760个逐时数据进行多元线性回归分析.建筑总能耗是我们关注的对象，设为反应变量，其它变量设为解释变量.根据多元线性回归方程的统计学使用条件，首先分别建立建筑总能耗与其它各解释变量的散点图，观察是否存在线性关系，由于篇幅有限，现给出建筑总能耗与给排水电耗、设备电耗的散点图，如图3、图4所示.

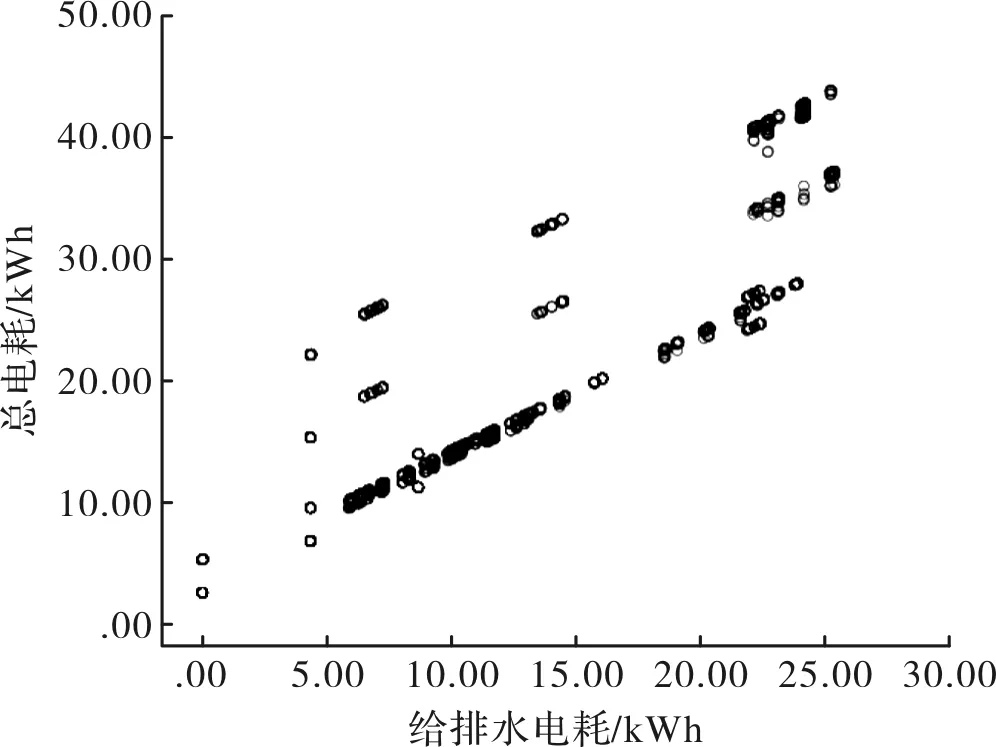
图3 建筑总能耗与给排水电耗的散点图Fig.3 Scatter diagram of total building energy consumption and electric energy consumption of water supply and drainage

图4 建筑总能耗与设备电耗的散点图Fig.4 Catter diagram of total building energy consumption and equipment dectric engergy consumption

从图3、图4可看出，建筑总能耗与给排水电耗、设备电耗成线性关系，实验结果表明，建筑总电耗与照明电耗、设备电耗、给排水电耗的线性关系较强，与温度、湿度、总辐射的线性关系较弱，由于影响因子较少，我们将六个解释变量均输入模型进行线性回归分析.

表3为回归系数估计及其检验表，模型常数项、温度、湿度、总辐射、照明电耗、设备电耗、给排水电耗的偏回归系数分别是9.032E-16、-5.292E-16、1.916E-14、4.081E-16、1、1、1.一方面，常数项、温度、湿度、总辐射的显著性值大于0.1，即不显著，通常不显著的预测变量都要从回归方程中删除；另一方面，由于温度、湿度、总辐射的偏回归系数和常数项的值很小，且温度、湿度、总辐射本身的值也不大，因此两者相乘的结果对建筑总能耗的影响可以忽略不计.结合西安实际情况，现有的高校宿舍未装空调，不涉及空调电耗，忽略温度、湿度、总辐射对宿舍空调电耗的影响也比较合理，于是可得到建筑总能耗的回归模型为：y=x4+x5+x6.从表3还可发现，宿舍类建筑的三大能耗中，与建筑总电耗的简单相关系数从大到小依次是给排水电耗(0.872)、照明电耗(0.693)、设备电耗(0.65).

表4为模型模拟的总体情况表，R方统计量为1表明该线性模型可以说明解释变量100%的变差，R方越大，说明模型的拟合效果越好.通过绘制残差的直方图，可判断残差εi服从正态分布，即残差间相互独立. Durbin-Watson值为0.299，实验样本数为8760，残差的协方差为0，即残差与解释变量相互独立.

表5为回归方程检验的方差分析表，可看出F值为4.046E+16，P值小于0.05，即该回归模型显著.

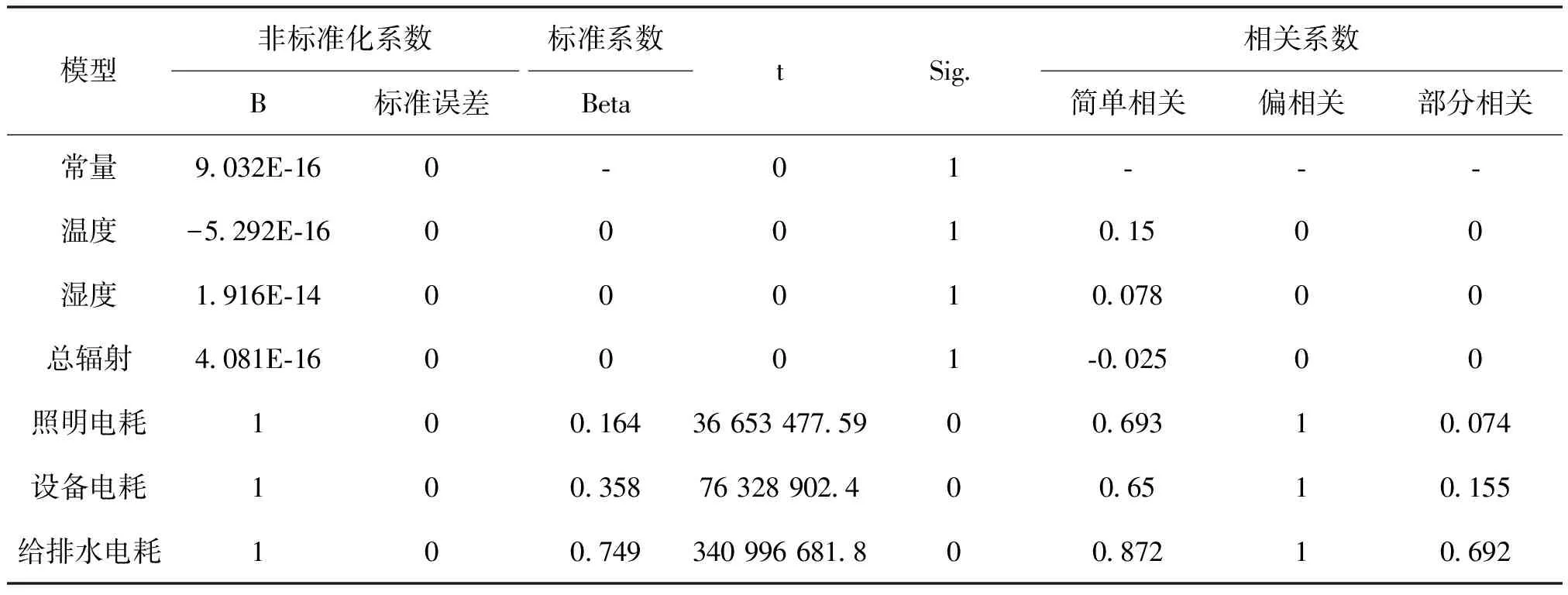
表3 回归系数估计及其检验

表4 模型模拟的总体情况

a.解释变量：给排水电耗，温度，照明电耗，总辐射，设备电耗，湿度

表5 方差分析

注：b.解释变量：给排水电耗，温度，照明电耗，总辐射，设备电耗，湿度

4 结论

本文以西安某高校的六层宿舍施工图为基础，通过DeST软件建立宿舍的简易模型，在忽略采暖能耗的影响的前提下设置相应参数，模拟得到包括温度、湿度、总辐射、建筑总能耗、照明电耗、设备电耗、给排水电耗在内的该宿舍全年8760个逐时的数据，并采用SPSS 22高级统计分析软件，以建筑总能耗为反应变量，其它变量为解释变量，建立了建筑总能耗与其它变量的多元线性回归方程，并对该模型做了残差分析和方差分析.实验结果表明，该模型拟合较好，宿舍总能耗与温度、湿度、总辐射的线性关系不明显，而与照明电耗、设备电耗、给排水电耗有较强的线性关系.在宿舍建筑的三大能耗中，与建筑总电耗简单相关系数从大到小依次是给排水电耗(0.872)、照明电耗(0.693)、设备电耗(0.65).因此，为推进高校宿舍节能，高校管理者应按照前后顺序，重点在给排水、照明和设备电耗这三方面着手，制定相应的政策及措施.本文可为进一步从事宿舍建筑的能耗预测方法及节能研究提供有益参考.