基于正态信息扩散的新多变量模糊时间序列模型研究

薛 晔，李肖肖，付恒春

（太原理工大学 经济管理学院，太原030024）

0 引言

时间序列分析方法不但可以从数量上揭示现象的变化规律，而且还能预测现象的未来行为，但在自然科学与社会科学研究中常常会存在一些具有模糊、不完备、或变量间相互关联等特性的时间序列。例如，货币流通情况通常可描述为正常、不正常、很不正常等模糊语义数据，这种经济现象的形成往往是受多种因素交互影响的结果。若用传统的时间序列模型对其变动趋势进行解释，很可能会导致模型判定偏差或预测结果和实际值间的误差。因此研究多变量模糊时间序列具有重要的理论和实践意义。

Song等[1，2]提出模糊时间序列的概念，并对美国阿拉巴马州的每年招生人数进行预测。Chen等[3]提出聚类算法，根据对样本数据的聚类结果确定各子区间的划分。Emrah[4]基于聚类分析建立模糊时间序列模型，以二变量C-均值聚类模型对租船费率做预测，以衡量模型精度的均方根误差显示该模型比传统模糊时间序列模型优越。Rubio等[5]根据与原始模糊逻辑关系相关的时间顺序，在模糊时间序列中使用新的加权算子来提高预测精度。Avazbeigi等[6]为预测伊朗公司的汽车工业产量，利用禁忌搜索算法构建了多元高阶模糊时间序列模型。邱望仁等[7]基于证据理论选取开盘价、最高价及最低价的243个日交易数据对沪市股指预测，并得出多变量模糊时间序列模型的预测精度高于单变量模型的结论。

综上所述，目前对于模糊时间序列模型的研究主要集中在大样本多变量或仅是单变量的的情况，但事实上大多是受多个变量影响且小样本的情况。鉴于此，本文结合信息扩散理论可以充分提取样本数据的信息，弥补样本不足的缺陷，构建一个正态扩散多变量模糊时间序列模型。

1 信息扩散

1.1 信息扩散基本原理

设X是给定样本，U是论域V的一个子集。从X×U到[0，1]上的一个映射，即：

则称X在U上的一个信息扩散。

如果μ(x，u)是递减的，即若，那么μ称为一个扩散函数，U称为一个监控空间。

∀g∈G，假定Xg的选定监控空间为是一个有序等距分割集合ugj所组成的集合，即为Ugj的区间长度。

1.2 多变量正态扩散函数

根据中心极限定理和大数定律，目前的经济行为和经济现象一般近似服从正态分布，因此，本文选取正态信息扩散函数[8]。

设∀xi∈X是一个r变量向量，即且令：，为X的选定监控空间。U中有个元素。令μ(g)为Xg在Ug上的一个扩散函数，记作

其中，hg称作第g个扩散系数。

注：对于每一个Xg，都有一个正态扩散函数的模糊集Fg与之对应，这一过程称为时间序列的模糊化。模糊集Fg不唯一，随着区间长度Δ与扩散系数h的变化而变化。

1.3 正态扩散系数确定方法

正态扩散系数h的选择直接影响着扩散函数的预测结果，若h越小，则函数结果就越不稳定；若h越大，则函数结果的分辨率就越低。因此针对小样本而言，h的确定显得尤为重要。目前应用最广泛的确定信息扩散系数的方法有两种：

（1）基于两点择近原则确定

（2）基于积分均方误差（MISE）最小原则确定

其中σ为样本观测值的标准差。

2 多变量模糊时间序列预测模型的建立

多变量模糊时间序列模型的构建主要步骤包括：（1）利用多变量正态信息扩散构造模糊信息矩阵；（2）运用模糊集理论构建模糊关系矩阵；（3）基于模糊近似推理方法建构多变量模糊时间序列预测模型。

2.1 模糊信息矩阵的建立

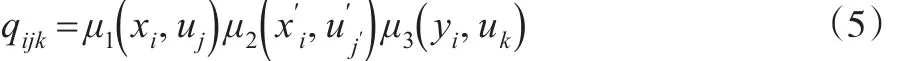
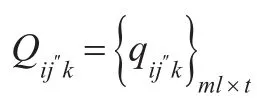
即：

于是W在上的模糊信息矩阵为：

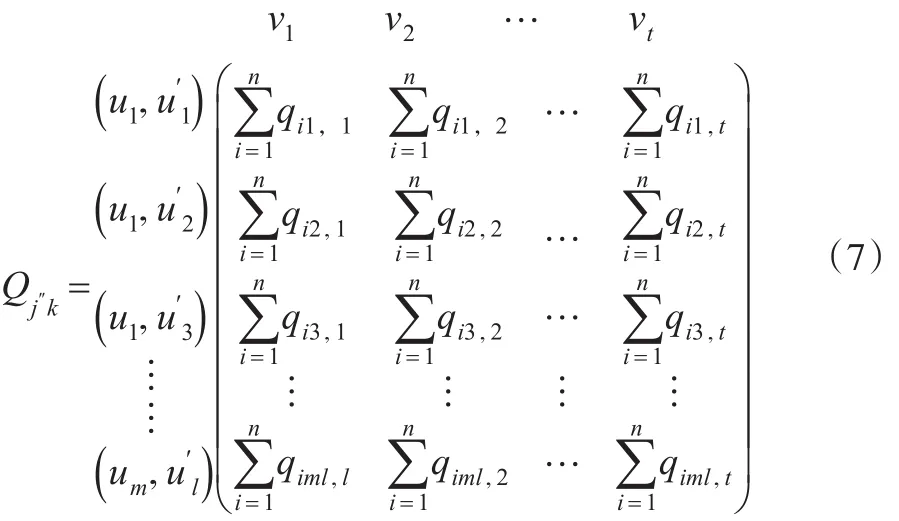
2.2 模糊关系矩阵的建立

依据模糊集理论，将式（7）转化为模糊关系矩阵式（9），具体计算如下：

则模糊关系矩阵为:

2.3 多变量模糊时间序列模型的建立

利用模糊近似推理方法建构多变量模糊时间序列预测模型：

考虑到模型的复杂度与模型精度，将“◦”选为“∨-*”，则正态扩散多变量模糊时间序列模型（NDMFTSM）：

注：（1）R随着hx、hy和hz的变化而变化。即，只要确定了hx、hy和hz，模糊关系矩阵R也随之确定。（2）基于正态信息扩散方法构建模糊关系矩阵的操作简单易行，可以避免大量复杂计算。

3 中国SO2排放量的预测

造成大气污染的重要因素之一SO2的过量排放不仅对人们生活质量及国家经济可持续发展存在着显著的负面影响，而且SO2与能源消耗、经济增长密切相关，因此本文选取度量能源消耗的能源消费总量（TEC）、度量经济总量的人均GDP（PCGDP）两个指标来预测二氧化硫排放量（ESO2）。

3.1 数据来源及预处理

本文选取的是2006—2016年TEC、PCGDF、ESO2的时间序列数据（见表1），数据均来自2007—2017年《中国统计年鉴》。

表1 TEC、PCGDF、ESO2的时间序列数据

为了减少分散程度和提高预测精度，将表1中数据进行对数预处理，即Y=ln(ESO2)，见表2所示：

表2 ln(T EC)、ln(P CGDF)、ln(E SO2)的时间序列数据

3.2 二氧化硫排放量的预测

3.2.1 NDMFTSM模型的预测

由表2样本数据可得：ax=12.985，bx=12.565；代入公式（3）可得选取论域：由式（5）至式（7）计算得到模糊信息矩阵：

由式（8）及式（9）可得模糊关系矩阵：

将模糊关系矩阵R25×5和信息扩散矩阵P，代入式（11）得到2007—2016年二氧化硫排放量的预测值F͂t，见表3：

表3 NDMFTSMh0的预测结果

为了与马尔可夫模型的预测结果进行比较，利用式（12）对表3结果计算模糊集重心GCt，另外，为了更清楚地显现不同模型预测结果的变化情况，进一步对GCt进行对数逆变换指数运算结果见表4第5列。

此外，进一步讨论信息扩散系数对模型预测精度的影响，将表2数据代入式（4）得到，再由式（5）至式（12）得到SO2排放量预测值见表4第6列。

表4 不同h情况下NDMFTSM对SO2排放量的预测值及误差

由表4可知，与NDMFTSMh0相比较而言，NDMFTSMhMISE的绝对误差较大，在2007年、2010年、2011年、2013—2016年的预测值与实际值的偏离较远。此外，表4第12行的MAE，32.741＜51.433；表4第13行的MAPE，0.016＜0.024，表明信息扩散系数对NDMFTSM的预测精度有影响，且小样本时，NDMFTSMh0的预测效果较好，即比较理想地反映了实际值的变动趋势，而NDMFTSMhMISE预测值的曲线波动较大，如图1所示。

图1 不同的信息扩散系数对模型精度的影响

3.2.2 Markov模型的预测

为了与NDMFTSM进行比较，选取一阶Markov模型[9]对2007—2016年中国二氧化硫排放量进行预测。设只受的影响，并且选取与NDMFTSM模型相同的论域U、U′与V。则：

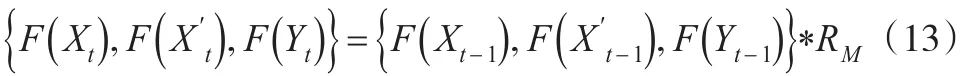
其中，RM为模糊马尔可夫相关矩阵，且：

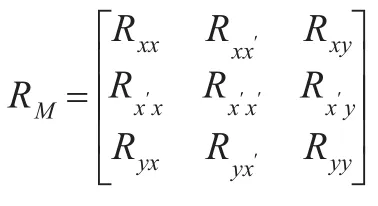
基于matlab7.0计算得到RM：

将表2数据以及RM代入式（13）得到二氧化硫排放量的预测值，具体结果见表5第4列。

表5 Markov对SO2排放量的预测值及误差

3.3 结果比较分析

依据表4和表5可知，NDMFTSMh0与NDMFTSMhMISE的预测结果与实际值的偏差均小于Markov模型，又因为32.741＜51.433＜81.984，0.016＜0.024＜0.040，所 以 NDMFTSM的预测误差较小，即模型精度较高，其中NDMFTSMh0的预测最优。相对而言，NDMFTSMh0较好地反映了实际值的变动趋势，NDMFTSMhMISE与Markov模型在预测期初以及期末都出现了不同程度的偏离，曲线波动比较大，如下页图2所示。主要原因在于Markov及NDMFTSM模型中的模糊关系矩阵R的建立方式不同，前者依据变量当期及滞后一期的时间序列F(Xt)及F(Xt-1)定义的“×”运算取得模糊关系矩阵RM，当变量个数增加或样本容量增大时，RM不仅可能出现模糊关系爆炸的现象，还需大量的运算时间；而NDMFTSM模型在小样本或信息不充分、不完备的情况下，仍可提取样本中更多的有用信息以弥补样本不足的缺陷，进一步提高模型的精度。对所建模型值得一提的是：随着样本容量的增大，模糊关系矩阵的计算难度不会增加反而还提高了模型的预测精度。

图2 实际值和NDMFTSM及Markov模型的预测结果

4 结论

本文利用正态信息扩散技术构建了一个多变量模糊时间序列模型，并讨论h0与hMISE对NDMFTSM的影响，进而与一阶Markov模型结果进行对比分析。结果表明：（1）信息不完备或小样本问题情况下，NDMFTSM利用正态信息扩散技术提高了模型的预测精度；（2）h影响NDMFTSM的预测精度；小样本时，NDMFTSMh0的预测精度更高；（3）在预测二氧化硫排放量时，NDMFTSM比Markov模型的预测效果好且计算过程方便简洁。需要指出的是，本文仅选取了两种比较常用的信息扩散系数的确定方法，虽然结果比较理想，但还是具有一定的局限性，下一步将对h的确定方法做深入研究。