基于投影图像SURF特征提取的三维模型配准
童立靖,刘博文
基于投影图像SURF特征提取的三维模型配准
童立靖,刘博文
(北方工业大学计算机学院,北京 100144)
针对传统三维模型配准方法存在对点云初始位置有一定要求、模型配准的精度有时不高等问题,提出了一种基于三维模型投影图像SURF特征提取的三维模型配准方法。首先通过扫描三维模型数据确定投影图像的范围,判断每个投影图像像素所隶属的模型网格,并求解从投影图像到纹理图像的映射关系,从而获取二维投影图像;然后对这两幅投影图像分别进行SURF特征点的选取与特征值的计算,并按SURF特征值进行特征匹配,再根据投影图像像素点与三维网格端点的映射关系计算三维特征点对;最后通过匹配的特征点对求取模型变换矩阵完成三维模型的配准。实验结果表明,该方法在配准时间变化不大的前提下,有效提高了配准精度,并具有较好的鲁棒性。
三维扫描;投影图像;SURF特征;图像配准;三维配准
三维点云配准技术是当前逆向工程、数字医学图像、计算机视觉、曲面质量检测等研究领域的热点与重点。三维点云配准的目标是求解近似的配准变换参数[1],经变换映射后让两组点云数据合并到一个统一的坐标系下,从而构成一个完整的三维数据模型。
现阶段,许多相关专家学者给出了较好的三维点云配准算法,主要有:文献[2]通过图像与图像的配准,以及模型与图像的配准,来完成三维生物图像的配准,但对于前者,其主要使用了随机抽样一致(random sample consensus,RANSAC))算法,对于后者,其使用了主骨骼模型。RANSAC算法,是目前应用性较强的三维配准算法。其随机选取一个点集,根据边长的比例关系,从目标点云中寻找对应的点集。与基于几何特征的配准算法相比,优点是可以处理初始位置相对较远的模型数据,缺点是选取的初始点集不同,会影响配准算法的效率。而对于主骨骼模型,一般的生物模型是具有的,但对于非生物个体模型是很难提取的。文献[3-4]是对迭代就近点(iterative closest point,ICP)算法的改进算法。文献[3]中的方法是通过逐步减小误差的上边界去避免ICP收敛于局部最优,但代价是算法的时间效率大为下降;文献[4]提出了一种基于期望最大估计的方法,解决ICP算法收敛组速度较慢和少量噪声引起的配准效果不佳问题,但对于复杂的且含有大量噪声的刚体碎块模型,配准精度和效果尚待改进。文献[5]在对三维点云数据进行配准时使用了一致点漂移(coherent point drift,CPD)算法,并对其进行了加速处理,但在配准时考虑了所有的点,对于部分重合的两个三维点云的配准不太适合。文献[6]为三维配准给出了一种快速的旋转搜索算法,但其前提是已知点云的平移参数,然而,对于仅能部分重合的点云模型配准,点云的平移参数是无法预知的。文献[7]使用最小二乘法进行多模态三维模型的配准,其核心是对特征点在不同尺度下的局部曲率及其与曲面距离的匹配,但对于曲面较为光滑且曲率较为一致的点云曲面配准,在鲁棒性方面难以取得较好的效果。
本文的配准方法主要是面向具有纹理数据的三维模型。一般三维扫描仪扫描的模型数据中,扫描仪在获取物体表面的点云数据同时,可以获取一种无规则的纹理图像。本文提出了一种利用无规则的纹理图像,获取模型的二维投影图像,从而利用投影图像的加速鲁棒特征(speeded up robust features,SURF)对三维模型进行配准的方法。算法首先读取两个三维模型数据;对两幅模型进行二维投影图像的获取;然后对两幅投影图像进行特征点匹配;最后求取三维特征点对求取模型变换矩阵从而完成三维模型的配准工作。实验表明,本文算法完成的三维模型配准的效果较好,具有较强的鲁棒性。本文算法的整体流程如图1所示。

图1 本文算法整体流程图
1 投影图像的获取
1.1 算法描述
通过三维扫描仪获取的纹理图像是散乱无规则的,利用采集的三维模型数据获取有序的二维投影图像的主要步骤为:①通过分析处理三维点云的坐标数据从而确定投影图像的范围;②对二维投影图像中隶属于网格投影区域的像素点进行判定与提取;③记录下每个提取的像素点对应的网格序号。算法具体流程如图2所示。

图2 获取二维投影图像流程
1.2 三维数据的分析和预处理
三维数据的分析和预处理的主要任务是对三维模型空间坐标点进行归一化和通过三维数据分析计算出二维投影图像的范围。
为获得完整清晰的投影图像,需要确定二维投影图像范围,具体生成的二维投影图像范围为
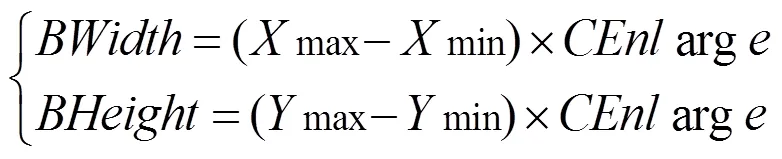
其中,、分别为投影图像的宽度和高度;max、min、max、min分别为三维点云数据坐标在、方向上的最大最小值;arg为选取的比例系数。
1.3 网格隶属像素的判定
根据模型文件中点云网格到纹理图像中的映射关系,可以从纹理图像中提取点云网格投影图像的像素信息,但在提取前首先需要确定各像素点所隶属的三角形网格。
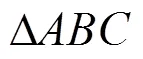
在完成各像素点的隶属网格判定后,记录每个像素点所在的空间三角形网格序号。
1.4 网格像素信息的提取
扫描仪获取的无规则纹理图像的像素点并非是有序排列的,某待配准的两个点云的无规则纹理图像如图3所示。
除三角网格顶点像素信息可以直接从纹理图像中提取外,其他点的像素信息是无法直接获得的。本文是通过像素点映射的方法来提取其像素点的信息的,因此需要首先求解出二维投影图像中每个三角形面片到无规则纹理图像的三角形面片的映射矩阵。假设每个三角形网格的顶点在二维投影图像上的坐标为(x,y),其对应的纹理坐标为(u,v)。利用三对坐标间的映射的关系可求变换矩阵,用齐次坐标表示向量和点,其映射关系为
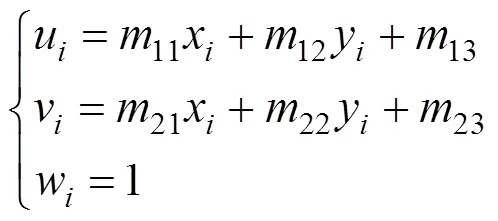
由式(2)可以求得变换矩阵,即
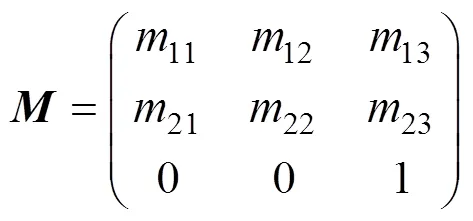
由于三角形内部各点,也都应遵循此映射关系,所以,根据求解的变换矩阵与式(2)可完成二维投影图像的每个三角面片中各像素点信息的提取。

图3 无规则纹理图像
2 投影图像的SURF特征提取
三维模型配准的前提在于寻找两幅三维点云的特征点对,本文算法中三维特征点对是依据二维投影图像的特征点对计算而来。因此首先需要进行投影图像的特征匹配。
图像配准算法可以分为基于灰度法的方法、基于特征的方法、基于变换域法的方法[8]等。目前较为常用的是基于特征的方法,主要有赵海峰等[9]提出的基于特征点Rényi的图像配准算法、梁枫和王平[10]提出的角点特征算法、LOWE[11]提出的SIFT特征提取算法、张雄美等[12]提出的改进SIFT特征提取算法以及在SIFT特征提取算法的基础上,BAY等[13]提出的SURF特征提取法等图像配准算法。
SURF算子在提取的特征点时对尺度变换和旋转变换具有不变性,这个特性对本文中获取的两幅二维投影图像之间的差异具有较好的容错性,有利于进一步三维数据的配准,因此本文采取基于SURF算子的特征提取与匹配算法。
2.1 SURF特征点的选取
为了完成三维点云模型的配准,需要首先从前面获得的投影图像中选择出一批特征点,以便进一步从三维点云中搜索特征点对。

Hessian矩阵的计算值在一定程度上表征了各点与周围临域像素的灰度差异,从而形成对应的图像。使用不同尺度的模版形成不同尺度的特征点响应值的金字塔图像,从而搜索到特征响应极值点。选取在最近26个临域值为极值的特征点,作为备选特征点。然后,通过在图像空间和尺度空间中进行的插值计算[15],得到最终的特征点坐标。
2.2 SURF特征值的计算
为了对投影图像中的特征点进行精确匹配,需要计算各特征点的SURF特征值。为此,首先计算各特征点的局部矢量:在特征点周围6的邻域内计算水平方向和垂直方向的哈尔小波值,并让其乘以不同的比例系数,使得远离特征点的响应贡献小,靠近特征点的响应贡献大;再利用60°的窗口进行360°的滑动,累加窗口内的哈尔小波响应,则该特征点的局部矢量定义为其最大值方向。
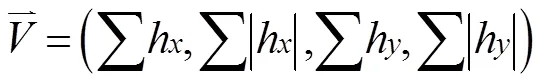
2.3 特征点匹配
分别计算出两幅二维投影图像的各特征点的SURF特征描述向量后,为了得到两幅投影图像中特征点的匹配关系,需要计算两个特征点的特征描述向量间的匹配程度。
设、分别为两幅投影图像提取的特征点集,对中各特征点p,计算出p与集合中所有特征点q的64维欧式距离d,即
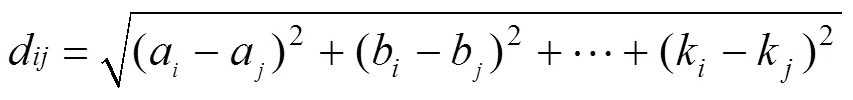

则认为p与d1所对应的q1为匹配的点对。
3 三维模型的配准
3.1 三维特征点对获取
要完成后续的三维模型配准,必须首先得到三维特征点对。本文获取的三维特征点对的方法是利用2.3节中获取的投影图像的匹配特征点对并且根据每个投影图像的像素点都唯一对应一个三维网格中的空间点而计算得到的。
首先计算二维特征点对应三维空间上的、坐标,即
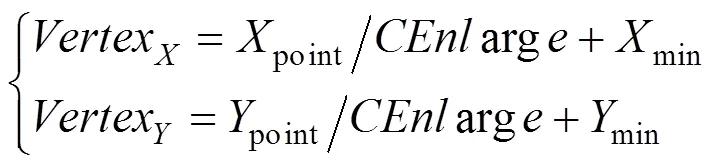
其中,Verte、Vertex分别为二维特征点对应的三维空间的、坐标;point、point分别二维特征点在投影图像中的、坐标。本文1.3节中,对于投影图像每一个像素点,都记录了对应的三角形网格序号,根据网格序号,计算出Verte、Vertex与对应三角形网格3个顶点的、坐标的欧式距离,然后选取距离最近的顶点为三维特征点,从而完成三维特征点对的获取。
3.2 三维模型的配准算法
三维模型配准的任务是根据三维特征点对计算出变换矩阵,将两幅点云数据统一到一个参考坐标系下。本文采取计算变换矩阵的方法如下:
(1) 设变换矩阵、变换前特征点集和变换后特征点集。则有=,即



(3)计算出、、、等4个参数的值,即
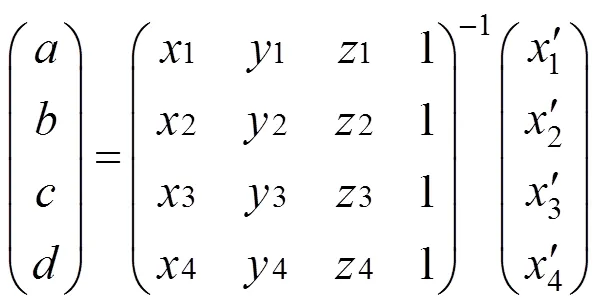
同理,可以计算出系数、、、、、、、的值,从而计算出映射矩阵。根据映射矩阵,对点云数据进行空间映射,并进而完成三维模型的拼接。
4 实验结果及分析
为了验证本文算法的有效性,进行了相关的三维扫描与配准的实验。实验的运行环境为:Inter(R) Core(TM) i7-4710MQ CPU @ 2.50 GHz,8 GB内存,Windows 10 64位操作系统,采用Visual C++编程在Visual Studio 2005平台下基于OpenGL和OpenCV实现。实验模型源自美国Artec Spider手持式高精度三维扫描仪。
对于某木偶模型,扫描仪分别采集了木偶的左半身和右半身,两个待配准的三维木偶模型如图4所示,其中扫描仪获得的无规则的纹理图像如图3所示。经过本文算法获取的两幅二维投影图像如图5所示。对图5的两幅投影图像进行特征匹配,结果如图6所示。为了进行相关的对比性实验,对图4待配准的三维模型使用RANSAC算法配准后的结果如图7(a)所示,使用ICP算法配准后的结果如图7(b)所示,使用本文配准算法后的结果如图7(c)所示。

图4 待配准木偶模型
为进一步验证本文算法的有效性与鲁棒性,使用了多种三维模型进行了相关实验,对于某头像模型和茶壶模型的实验结果如图8、9所示,某1号人脸模型和2号人脸模型的实验结果如图10、11所示。并将本文算法分别从配准精度、运行时间上与RANSAC算法和ICP算法进行了比较。配准精度的衡量采用计算均方误差的形式来验证。对比实验数据见表1、2。
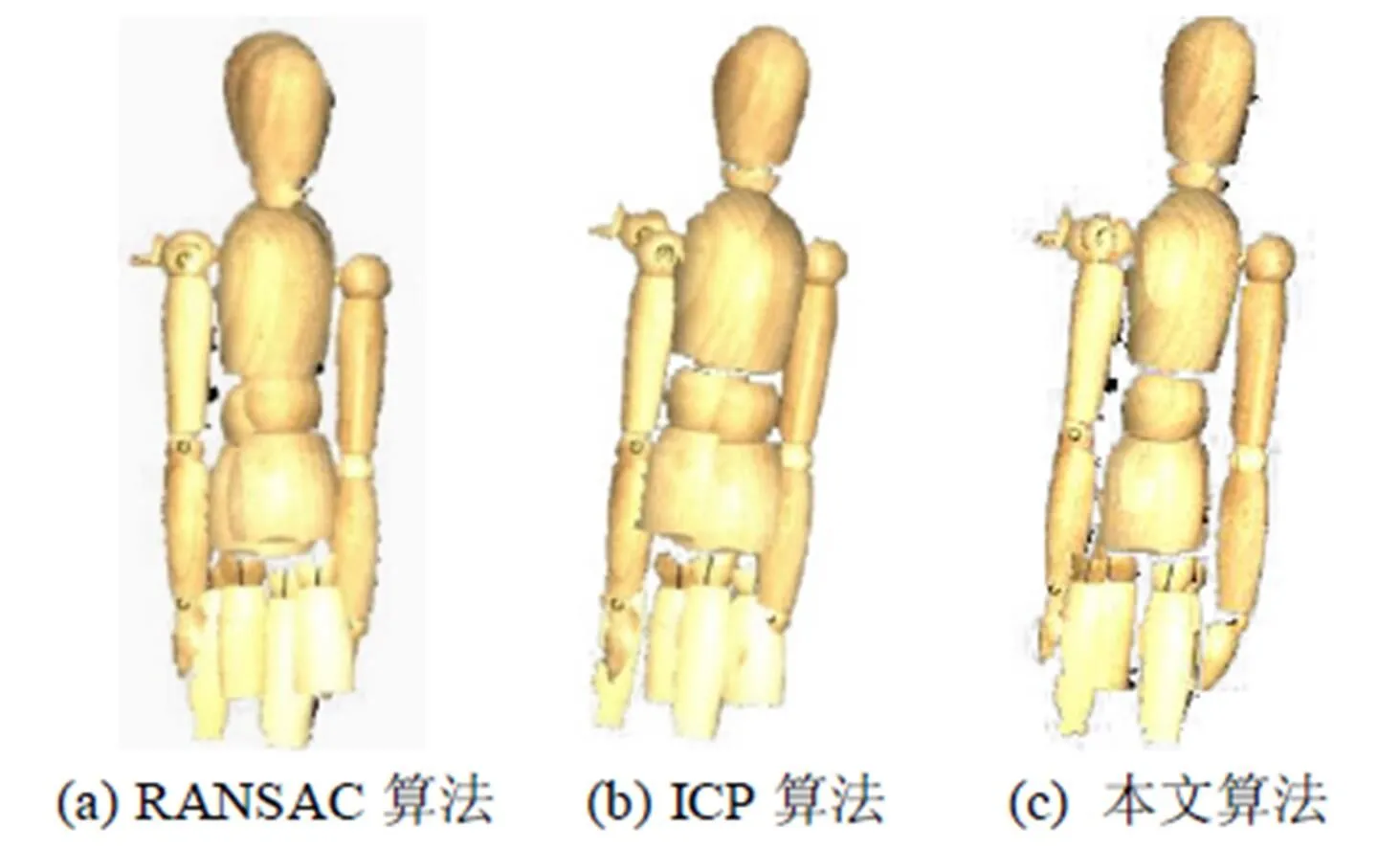
图7木偶模型配准结果

图9 茶壶模型的配准
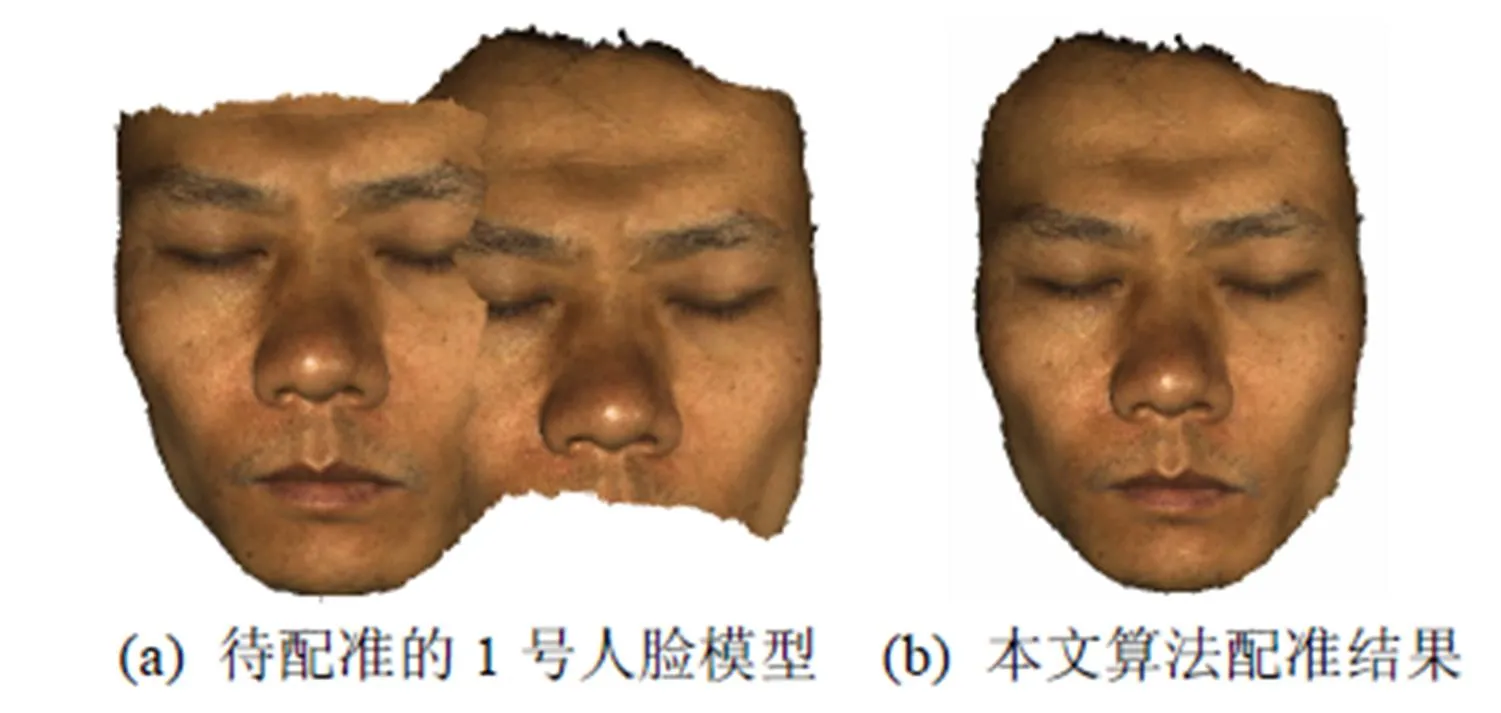
图10 1号人脸模型的配准

图11 2号人脸模型的配准

表1 其他算法与本文算法均方误差值(mm2)
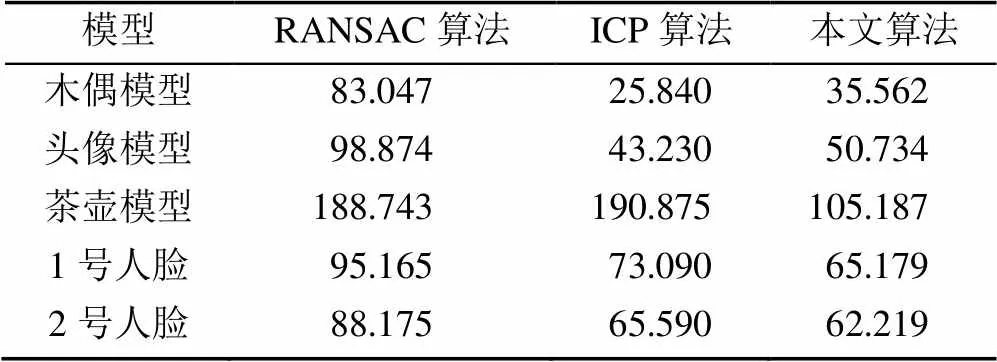
表2 其他算法与本文算法的时间比较(s)
实验结果表明,本文算法配准结果的均方误差值较小,并且可以较好地适应不同点云初始位置与不同曲率分布的三维模型配准。如在初始位置相距较远的头像模型、1号人脸模型、2号人脸模型,如图8、10、11所示,本文算法相对ICP算法与RANSAC算法有较好的配准精度;对于交叉程度较大,并且许多地方点云曲率较为相近的茶壶模型,如图9所示,本文算法的配准精度也较RANSAC与ICP理想。而就运行时间而言,本文算法的平均运行时间也略优于RANSAC算法和ICP算法。
5 结束语
本文提出了一种面向三维模型的SURF特征提取与配准的方法。该方法能够将扫描仪获取的无规则的纹理图像转化为三维模型的二维投影图像;并进行SURF特征提取与匹配;依据二维投影图像像素点与三维网格上空间点的一一对应的映射关系,找到两幅点云数据的三维特征点对;从而求取映射变换矩阵,并最终完成三维模型的配准工作。实验结果表明,该方法在配准时间变化不大的前提下,有效的提高了配准精度,并具有较好的适应性。对于如何在保证三维模型配准精度的前提下,进一步提高配准速度是未来研究工作的重点。
[1] 肖慧敏. 点云数据的配准算法[D]. 西安: 西安电子科技大学, 2013.
[2] LEI Q, FU H L,HAN C P. 3D registration of biological images and models [J]. IEEE Signal Processing Magazine, 2015, 32(1): 70-77.
[3] YANG J, LI H, CAMPBELL D, et al. Go-ICP: a globally optimal solution to 3D ICP point-set registration [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(11): 2241-2253.
[4] 赵夫群, 周明全. 改进的概率迭代最近点配准算法[J]. 图学学报, 2017, 38(1): 16-22.
[5] LU M, ZHAO J, GUO Y L, et al. Accelerated coherent point drift for automatic three-dimensional point cloud registration [J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(2): 162-166.
[6] BUSTOS A P,CHIN T J,ENIKSSON A,et al. Fast rotation search with stereographic projections for 3D registration [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(11): 2227-2239.
[7] MELLADO N, DELLEPIANE M, SCOPIGNO R. Relative scale estimation and 3D registration of multi-modal geometry using growing least squares [J]. IEEE Transactions on Visualization and Computer Graphics, 2016, 22(9): 2160-2171.
[8] 殷伶. 图像匹配技术的研究[D]. 西安: 西安电子科技大学, 2010.
[9] 赵海峰, 陆明, 卜令斌, 等. 基于特征点Rényi互信息的医学图像配准[J]. 计算机学报, 2015, 38(6): 1212-1221.
[10] 梁枫, 王平. 基于角点特征的高精度图像配准算法[J]. 重庆理工大学学报: 自然科学, 2010, 24(2): 87-90.
[11] LOWE D G. Distinctive image features from scale-invariant key points [J]. International Journal of Computer Vision, 2004, 60(2): 91-110.
[12] 张雄美, 易昭湘, 蔡幸福, 等. 基于改进SIFT的SAR图像配准方法[J]. 计算机工程, 2015, 41(1): 223-226.
[13] BAY H, ESS A, TUYTELAARS T, et al. Speeded-up robust features (SURF) [J]. Computer Vision and Image Under-standing, 2008, 110(3): 346-359.
[14] 巨刚, 袁亮, 刘小月, 等基于改进SURF算法的移动目标实时图像配准方法研究[J]. 通信学报, 2017, 38(1): 177-186.
[15] BROWN M, LOWE D. Invariant features from interest point groups [EP/OL]. [2018-02-20]. https://wenku. baidu.com/view/ab6d10c608a1284ac85043b9.html.
3D Model Registration Based on SURF Feature Extraction of Projection Images
TONG Lijing, LIU Bowen
(College of Computer Science and Technology, North China University of Technology, Beijing 100144, China)
In order to solve the problems with the traditional 3D model registration methods, such as the higher requirements for the initial locations of the two point clouds and the lower accuracy of model registration sometimes, a 3D model registration method based on SURF feature extraction of the two 3D model projection images is proposed. Firstly, the range of the projection image is determined by the 3D model data, and the model grid which each projection image pixel belongs to is deduced. Thus the two-dimensional projection image can be calculated by the mapping relationship from the projected image to the texture image. Then, the SURF feature points and the eigenvalues are calculated for the two projection images respectively. The feature matching is performed according to the SURF eigenvalues. Next, the feature point pairs in the two 3D models are extracted through the mapping relations between the 3D models’ grid vertices and the projection image pixels. Finally, the two 3D model registration is implemented through the transformation matrix which is calculated from the matched feature point pairs in the two 3D models. The experimental results show that this method can improve the registration accuracy effectively and has good robustness under the condition of little change in registration time.
3D scanning; projection image; SURF feature; image registration; 3D registration
TP 391
10.11996/JG.j.2095-302X.2018061117
A
2095-302X(2018)06-1117-06
2018-03-14;
2018-04-20
国家自然科学基金项目(61371142);北京市教委科技创新服务能力建设项目
童立靖(1972-),男,安徽马鞍山人,副教授,博士,硕士生导师。主要研究方向为计算机图形学、数字图像处理等。E-mail:ljtong@ncut.edu.cn

