一类部分线性时间序列模型的估计及其应用

王明辉 ，卢俊岚

（1.韶关学院 数学与统计学院，广东 韶关 512005；2.韶关学院 外语学院，广东 韶关 512005；3.暨南大学 经济学院，广东 广州 510632）

时间序列分析，包括线性时间序列求和自回归移动平均（ARIMA）模型，非线性时间序列自回归条件异方差模型和广义自回归条件异方差模型等［1］，近年来发展较为迅速，研究日趋成熟，理论成果较为丰富，并得到了非常成功的应用［2］.半参数时间序列模型是一类非线性时间序列模型的统称，包括可加、单指标和变系数等模型，其中一种较为简单的模型为部分线性模型.Yu等［3］对于具有独立同分布误差项的非线性自回归模型，首先假定回归函数来自某个参数分布族，使用局部二次拟合准则和条件最小二乘方法得到参数估计量，然后为了降低估计量的误差，运用非参数核方法进行调整，最后证明了回归函数估计量具有弱相合性.Farnoosh和Mortazavi［4］则将该方法运用到具有一阶自相关误差项的非线性自回归模型中，同样证明了所得回归函数估计量具有弱相合性，并对伊朗商业银行的年度存款数据进行实证分析，验证了该模型的可行性和有效性.本文则从另一角度对文［3］做一拓展，将其方法应用到部分线性时间序列模型中，并使用韶关GDP数据检验方法的可行性和有效性.

1 部分线性时间序列模型及其估计

本文主要研究部分线性时间序列模型：

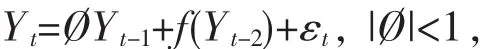
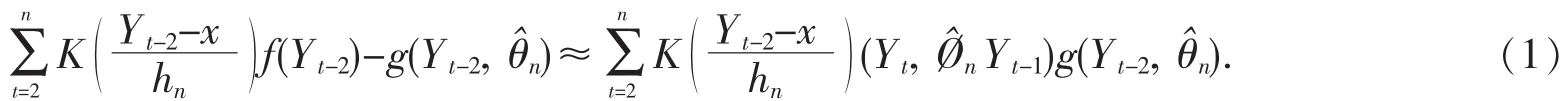
2 韶关GDP的实证分析

2.1 数据预处理

在以往涉及GDP的研究中，所采用的方法多为多元线性回归、时间序列分析和灰色预测等方法.特别地，在涉及韶关GDP的文献中，林嘉和张宗君［5］运用线性回归方法研究了韶关市财政收入与GDP之间的内在数量关系，揭示了影响财政收入增长的主要因素，提出了促进二者协调发展的对策建议；陈焕荧［6］从韶关市义务教育资金的投入规模、支出结构、产出效益3个角度进行了研究和分析，得出制约财政经费绩效提升的主要因素，提出改进政府政绩考核制度、调整义务教育经费结构、提升义务教育经费绩效、改善义务教育经费评价制度等方面的一些建议.本文则从部分线性模型的角度，对1978—2016年的韶关 GDP（1978年=100）数据做分析，进一步说明本文所用方法的有效性，原始数据Yt来源于《韶关统计年鉴2017》，对于Yt*=Yt/1 000绘制时序图.

从图1可看出该序列在这39年间呈曲线增长趋势，显然非平稳，而一阶差分后仍显示不平稳，但二阶差分后在显著性水平0.05下，变为白噪声序列，因此不适合采用ARIMA模型进行拟合.

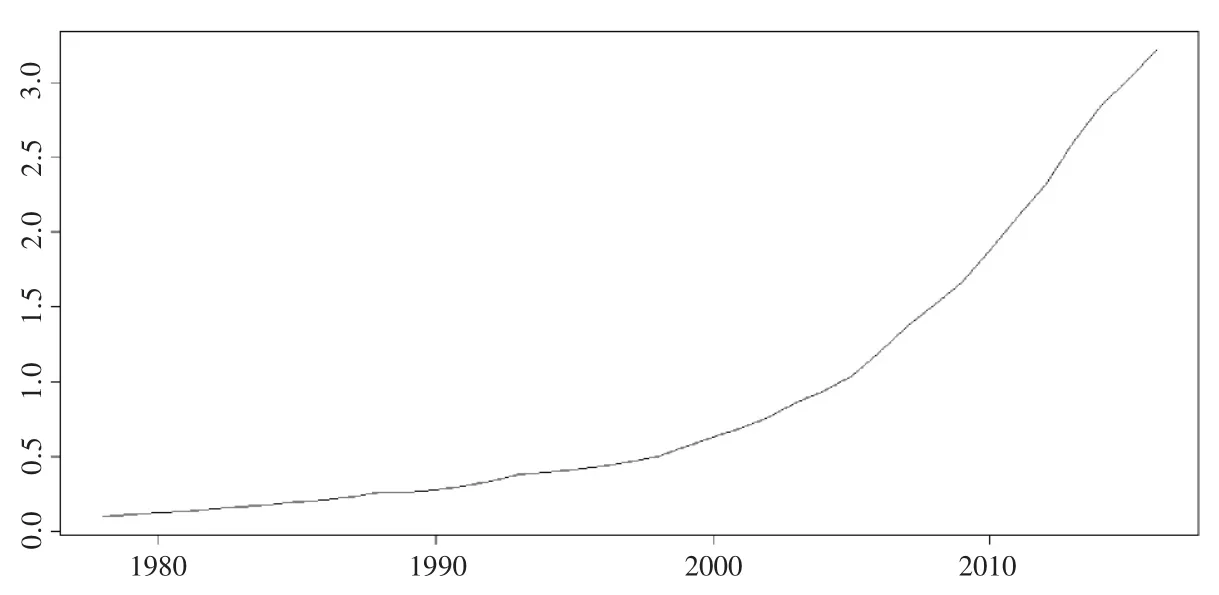
图1 韶关市GDP时序图

2.2 模型建立

取 g(x,θ)=θex，建立部分线性时间序列模型，所得拟合方程如下：

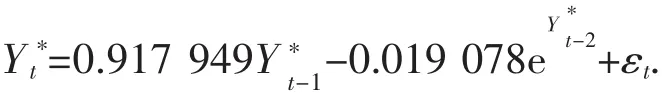
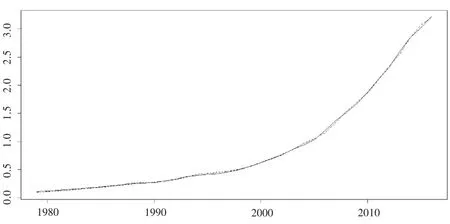
图2 的真实值（实线）与估计值（虚线）对比图

2.3 模型检验

对参数进行显著性检验结果见表1，因此在0.05的显著性水平下，两个参数均显著.

表1 参数显著性检验结果

图3为残差序列的Q-Q图，用来描述残差序列是否服从正态分布.图中的数据点基本上按照对角直线排列，趋于一条直线，并被对角直接穿过，且有95%的样本点落在［-2,2］区间内，故应认为残差序列近似服从正态分布.采用Shapiro-Wilk正态性检验方法，所得统计量的值为0.956 73，对应的值为0.148 4，也印证了残差序列具有正态性，两者从侧面反映了本文方法的拟合效果。

2.4 模型预测

图3 残差序列Q-Q图

表2 未来三年的预测值

2.5 与其他模型的比较

如前所述，该韶关GDP序列不适合采用ARIMA模型进行拟合，为了检验本文方法的有效性，采用二次回归、三次回归、指数回归和幂模型分别进行建模，各方法所对应方程如下：

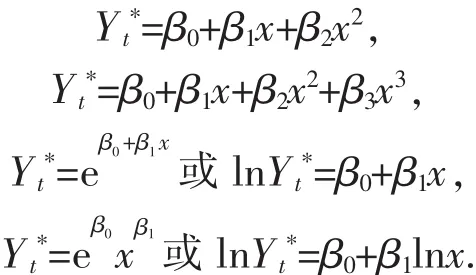
表3列出了本文所用方法与其他方法的参数估计和模型汇总.经过显著性检验，发现上述模型的拟合方程均在0.05的显著性水平下显著，同时模型残差也能通过正态性检验.只有两个参数在该显著性水平下不显著，删除这两个参数后的拟合方程也包含在表中.与其他方法相比，本文方法拟合效果较好，具有一定的优越性.

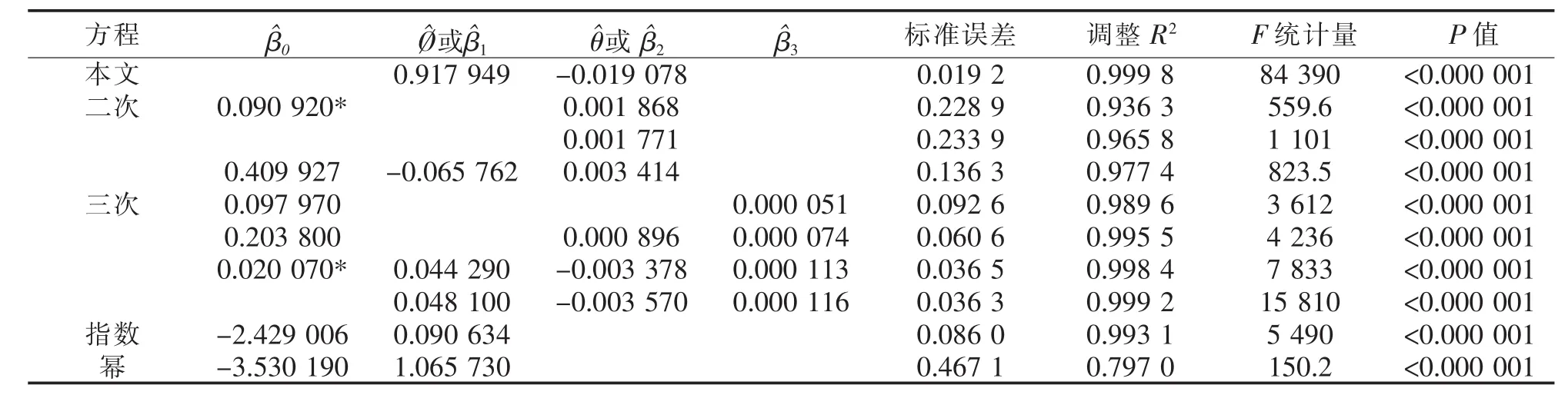
表3 参数估计和模型汇总

3 结论和建议

本文以一类部分线性时间序列模型为基础，引入一阶自回归项的线性分量和二阶自回归项的非线性分量，可在一定程度上避免线性时间序列模型的缺陷.采用本文模型分析韶关GDP的变化特征，利用1978—2016年的数据建立模型，预测了未来3年的数值，给出了其95%的置信下限和上限

本文的建模方法也存在一定的难点和不足.首先，模型的定阶存在一定难度，Yt滞后阶数的确定暂时没有较为完善的方法.其次，参数分布族{g(x,θ);θ∈Θ}的确定也具有一定的难度，且直接影响模型的拟合效果.再次，误差项{εt}有可能非独立同分布随机变量.这些难点都对研究者提出较大挑战，需要较为准确地把握住数据本身的趋势.