基于共轭梯度法和全变差正则化的图像复原

张彬，孙菁聪，王胜文

(中国传媒大学理学院，北京 100024)

1 引言

图像复原的目的是将原始图像从观察到的降晰图像中恢复出来。实际的降晰函数可以看作一个低通滤波器，使得原始图像的高频成分受到抑制甚至丧失。这个降质过程可以描述为如下的数学模型：

(1)

其中，f(x，y)为原图像，g(x，y)为观测到的退化图像，t(x，y)为空间不变的点扩散函数，n(x，y)为高斯白噪声。对该模型离散化后，将离散退化图像、离散源图像和离散噪声图像分别按照列字典序依次排列，可得三个列向量g、f和n，它们满足如下的线性方程组：

g=T·f+n

(2)

其中T是一个分块Toeplitz矩阵。

一般来说由于方程(2)是病态的，不能直接求解。因此必须添加一些先验约束以使问题正则化。为了更好地保留图像的细节信息，本文以图像的全变差为约束项，求解下述泛函的极小化问题

(3)

2 全变差函数的离散化和基于共轭梯度法的正则化复原算法

对于二元函数f(x，y)，其全变差TV(f)定义为

在单位正方形的水平区间内插入nx个等分点，在竖直区间内插入ny个等分点，于是有分点(xi，yj)，xi=i·Δx，yj=j·Δy，0≤i≤nx，0≤j≤ny，取f(x，y)在这些离散点的值得离散图像

将上述图像按列字典序排列，得向量f。

f=(f0，0f1，0…fnx，0f0，1f1，1…

fnx，1…f0，nyf1，ny…fnx，ny)T

为方便计算，可将面积元素ΔxΔy合并到正则化参数α中，于是Jβ(f)离散化为

利用方向导数与梯度的关系，可以求得Jβ(f)的梯度。

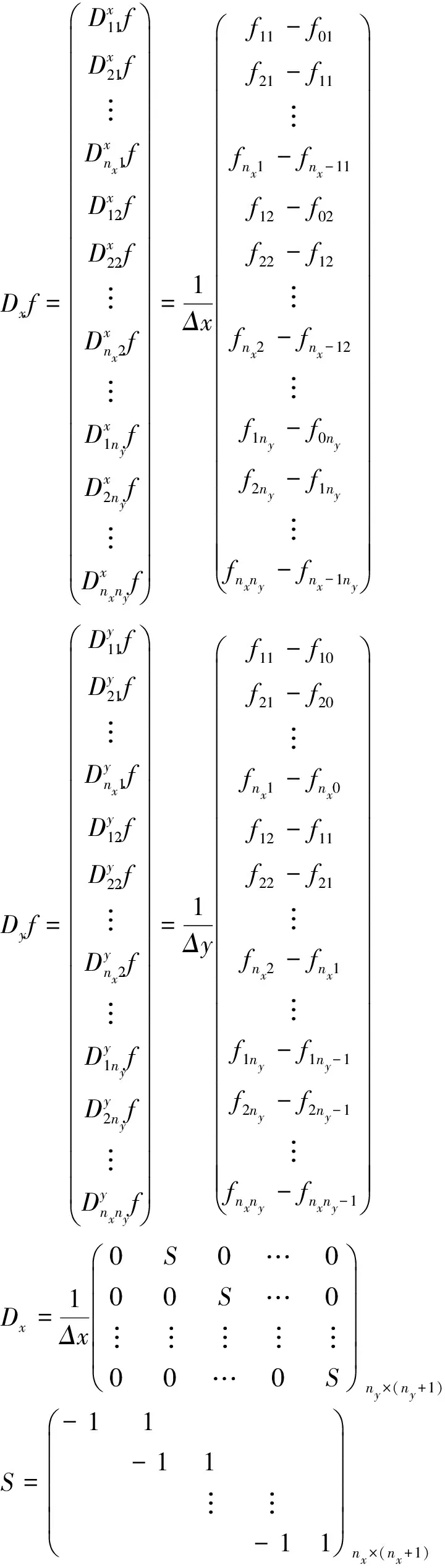
则有

上述梯度计算可按照分块Toeplitz矩阵与向量乘积的计算.

从(4)式可以得到Jβ(f)的梯度，把它用矩阵表示为

(5)

对基于全变差正则化的极小问题

其梯度为TT·(T·f-g)+α·L(f)

从而该极小化问题等价于求解线性方程组

(TT·T+α·L(f))·f=TT·g

(6)

利用共轭梯度法求解该线性方程组时，需要计算梯度向量(TT·T+α·L(f))·f-TT·g

其中T是分块Toeplitz矩阵，TT·T·f，TT·g都可按分块Toeplitz矩阵与向量乘积的方法来计算[1]，而L(f)·f主要是计算Dx·f和Dy·f，显然它们满足下面的关系

(7)

线性方程组(6)可用共轭梯度法CGM(conjugate gradient method)来求解。它仅需利用一阶导数信息，克服了最速下降法收敛慢的缺点，又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点，是解决大型线性方程组最有用的方法之一[2]。共轭梯度法的求解步骤如下：

1、给定迭代精度0≤ε≤1和初始点f0，计算初始梯度g0=(TTT+αL(f0))·f0-TT·g，令k：=0

2、若‖gk‖≤ε，停止计算，输出f*≈fk

3、计算搜索方向dk，

gk+1=(TTT+αL(fk+1))·fk+1-TT·g

5、令k：=k+1，转步2.

3 仿真实验及数据分析

为方便计算，选取两幅大小200×200的汉字“王”和“爷”的灰度图像Wang和Ye，moonfcce图像及rice图像作为原始图像。为了模拟因大气湍流而导致的图像模糊，选取高斯函数为点扩散函数，并取高斯函数的方差为0.03，并给模糊图像附加方差为10的白噪声。

图1的(a)、(d)、(g)、(j)为原始图像，(b)、(e)、(h)、(k)为模糊图像，(c)、(f)、(i)、(l)分别为以模糊图像为迭代初始向量，利用共轭梯度法迭代500次而得的复原的结果。为了得到较好的复原效果，四幅复原图像的正则化参数分别选取为0.000089，0.000065，0.000035和0.000065。

(a) (d) (g) (j)

(b) (e) (h) (k)

(c) (f) (i) (l)图1 四幅源图像、模糊图像和复原图像

对复原图像的客观评价一般采用无参考图像质量评价方法。无参考图像质量评价方法就是在没有一个可以进行参考和对比的原始图像的情况下，得出一个与人类视觉系统的视觉感知相一致的质量分数值的方法。近些年来，无参考图像质量评价得到了越来越多的关注。常用的有灰度平均梯度(Gray Mean Grads，GMG)及拉普拉斯算子和(LS)。

灰度平均梯度是分别将图像长度和宽度方向上的相邻像素灰度值的差求平方和再求均方根，它能较好的反映图像的对比度和纹理变化特征，其值越大表示图像越清晰，图像质量越好。

拉普拉斯算子和是对每一个像素点在 3×3 的邻域内采用拉普拉斯算子得到8邻域微分值，然后在图像范围内求和。一幅图像越清晰，轮廓越鲜明，则每一个像素点附近的灰度值变化越大，LS值就越大。

灰度平均梯度值与拉普拉斯算子和虽然都不用参照原始图像进行计算，但它们的值对于不同目标所成的不同图像由于背景、对比度及纹理结构等成像条件不一样差别是很大的，不具有可比性，因此只能用于对相同目标图像质量的比较，也可以用于比较对同一幅图像经过不同处理手段后的质量以判断处理方法的效果和有效性。

表1给出了上面四幅图像分别经过500次迭代后的GMG值LS值。

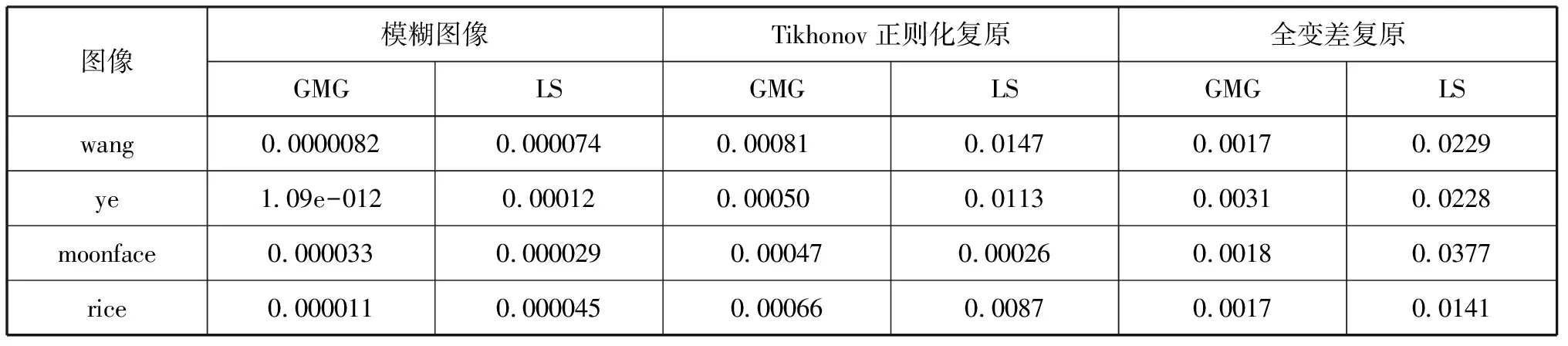
表1 各图像在Tikhonov正则化复原，全变差复原循环预条件的GMG值和LS值Table 1 GMG and LS of images

从表1可以看出，全变差图像复原的GMG值及LS值显然比Tikhonov正则化复原的GMG值和LS值要大，即图像的复原效果要比较好。