碰撞过程中两个常用结论的证明

朱磊

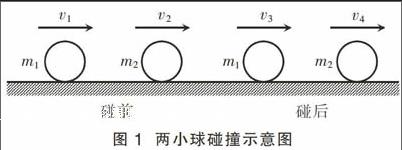
摘 要：以动量守恒、能量守恒为基础，利用不等式、二次函数、导数等数学方法，证明了两个常用结论：碰撞过程中完全非弹性碰撞能量损失最大；两同向运动物体正碰，当发生弹性碰撞时被碰物体获得的速度最大，发生完全非弹性碰撞时被碰物体获得的速度最小。

关键词：能量；动量；碰撞；导数

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2018）1-0042-3

1 引 言

能量和动量的有关知识是高中物理学习的重点也是难点。能量问题是人教版必修二中的内容，动量问题是人教版选修3-5的内容。在新考试大纲中将选修3-5作为必考模块后更加突出了动量的重要性。在学习了机械能、动量和冲量之后，接下来需要学习动量守恒定律。学习这个定律的一个重要作用是其在碰撞过程中的应用。高中物理中的碰撞过程比较简单，必须要掌握的是对心碰撞、弹性碰撞和完全非彈性碰撞。在这部分内容的教学过程中需要用到两个重要的结论性知识点：

第一，两个物体发生碰撞，当它们碰后结合到一起时，系统机械能的损失最大。

第二，一个物体被另一同向运动的物体正碰，当发生弹性碰撞时被碰物体获得的速度最大，发生完全非弹性碰撞时被碰物体获得的速度最小。

在教学过程中这两个知识点一般是直接作为结论强加给学生，基本不会给出推导过程，或者只是给予定性的推导。只要是稍微有点独立思考能力的学生，对于这样的教学过程不会满意，会产生为什么是这样的疑问？由于证明过程过于复杂，而且现有资料也很少针对这两个结论给出完整的证明。当学生产生疑问时，老师的回答基本上是：这是结论，直接用就可以了。这样处理学生的疑问不但显得教师的教学态度不严谨，而且损害了学生的探索精神。这两条结论性知识点的证明过程是将物理原理和数学知识结合在一起进行逻辑推演，很好地体现了演绎法的威力。我们在教学实践中发现，如果能针对这两个结论给予适当的证明，哪怕是给出一定的证明思路，对学生的学习热情都是一个很大的鼓舞。虽然大学课本中对第一个结论给出了证明，但其推导过程运用的方法已经超出了中学物理的知识范畴。那么，能不能在高中物理知识的范围内证明这两个结论呢？回答是肯定的。本文针对这两个结论给出了一种中学生能理解的证明。

2 证明

首先证明：两个物体发生碰撞，当它们碰后结合到一起时，系统机械能的损失最大。

现在来分析这两个解所对应的运动状态。

由于v4的最大解是在不等式取等号时求得的一个解，也就是在完全弹性碰撞条件下得到的，那么也就证明了在完全弹性碰撞的情况下，被撞小球有最大速度。

那么，v4最小解等于v2是什么含义呢？其实，是在入射小球还没有碰到被撞小球时保持的原速度。由于被撞小球一旦被撞一定加速，被撞小球所有的碰撞后速度一定大于被撞前的原速度，所以这是一个没有什么价值的平凡解。需要进一步证明两球发生碰撞后，发生完全非弹性碰撞时所具有的速度是所有被撞小球碰后速度的最小值。

除了动量守恒和能量不增加外，还有一个隐含的条件没有用。那就是在碰撞前后被撞小球的碰后速度不能小于入射小球的碰后速度。即

v4≥v3（19）

将（3）式代入到（19）式中，整理可得

很显然，当不等式取等号时，v4的值恰好和（7）（8）两式的值相等，也就是两球结合在一起所具有的共同速度。这也就证明了，在发生完全非弹性碰撞后被撞小球的速度有最小值。

至此，第二个结论得到证明。

3 总 结

碰撞过程的问题需要能量、动量和数学三方面知识的联合运用才能解决。在碰撞过程中由于内力比外力大很多，动量绝大多数情况下可以看作守恒，但是除了在理论和微观等少数情况下能量是不守恒的。以动量守恒和能量不增加两条基本原理，使用不等式、二次函数和导数等数学工具，推导出在碰撞过程中能量损失的最大值和被碰小球在碰后的速度范围。有了对这两个重要知识点的严格证明，使学生对这两个结论的运用更加心中有底，并且让他们对物理学中的物理原理与数学结合进行推理的演绎法有更加深刻的认识，有利于学生科学素养的提高。

参考文献：

[1]张妮.物理探究式教学设计案例《动量和动量定理》[J].物理教学探讨，2016，34（8）：38-44.endprint