对流层散射衰落信道下OQAM/OFDM系统分析
张 凯,薛伦生,陈西宏
(1.中国人民解放军95425部队,云南 曲靖 655331; 2.空军工程大学 防空反导学院,陕西 西安 710051)
0 引言
对流层散射通信技术由于其良好的越障能力,在军用通信领域具有重要的作用[1-2],随着对带宽需求的加大,大容量对流层散射通信技术已经成为国内外的研究热点[3-4]。但散射信道是一个典型的多径传播信道[5-6],为了克服多径信道对宽带通信带来的频率选择性衰落,目前通常采用正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术[7-8]克服多径。
OFDM技术是一种典型的多载波传输技术,对多径带来的符号间干扰具有良好的抑制作用[9-10],但其要引入循环前缀(Cyclic Prefix,CP)来消除多径扩展的影响,同时其对信道的多普勒频移十分敏感,载波间干扰严重。针对OFDM系统的不足[11-12],本文将基于偏移正交幅度调制的正交频分复用[12-13](Offset Quadrature Amplitude Modulation/ OFDM,OQAM /OFDM)技术应用于散射通信中[14]。文献[15]研究了OQAM/OFDM系统在时间和频率选择性衰落信道下的信道估计问题。文献[16]对时变多径信道下OQAM/OFDM系统进行分析,并研究了克服载波频偏的方法。文献[17]研究了OFDM技术在散射通信系统中的应用,并从理论上分析了OFDM系统在对流层散射衰落信道下的系统性能。目前还没有文献对散射信道下的OQAM/OFDM系统进行分析,因此,本文对散射信道下的OQAM/OFDM系统进行分析,通过对接收信号中的有用信号和干扰分量进行分析和计算,推导出系统的信号干扰比(Signal-to-Interference Ratio,SIR),进而得到在不同多径时延下系统的最佳符号周期。
1 OQAM/OFDM技术基本原理
OQAM/OFDM系统发送端发送的信号为:
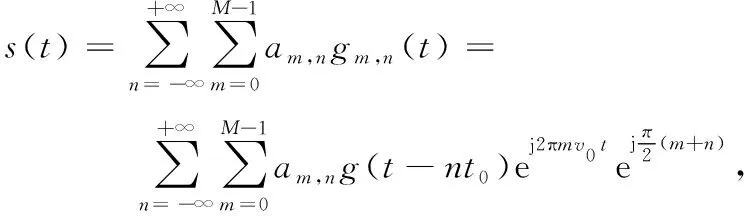
(1)
式中,am,n为第m个子载波上的第n个实数符号;gm,n(t)为在时频坐标点(m,n)处的滤波器函数;g(t)为成形滤波器的基函数;v0,τ0分别为OQAM/OFDM系统子载波间隔和发送信号时间间隔,满足v0=1/(2τ0)。
发送信号经过无失真信道,假设在接收端信号可以完美重构,接收端的接收到的信号为:
r(t)=s(t)*δ(t)。
(2)
接收到的信号经解调后输出为:
(3)
〈gm,n,gm0,n0〉R表示对gm,n和gm0,n0进行内积并取实部。
在OQAM/OFDM系统中,发送端和接收端滤波器满足在实数域正交,即
〈gm,n,gm0,n0〉R=δm,m0δn,n0,
(4)
δm,m0与δn,n0表示2个狄拉克函数。
2 对流层散射信道
信号在对流层散射信道中传输时,主要受到传输损耗和信道的衰落的影响,信道衰落又分为慢衰落和快衰落特性。其中传输损耗和信道的慢衰落是在通信链路层设计时需要考虑的影响,本文主要考虑快衰落特性。快衰落是指散射信号在短时间内的快速波动,主要由多径效应和多普勒效应描述[18-19]。
2.1 多径效应
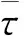
(5)
(6)
式中,p(τ)为功率延迟分布,有时也用最大时延扩展τmax来表示。本文根据最大时延扩展τmax来进行系统的参数设计。
2.2 多普勒频移
在对流层散射通信中,由于散射体的随机运动造成的信号频率发生偏移的现象就是多普勒频移。多普勒频移造成衰落信道的频率扩散,引起信号的时间选择性衰落。
由于散射信道的快衰落特性,对散射信道进行建模时典型的信道模型有Kailath提出的抽头延迟线散射信道模型和Sunde提出的Sunde模型,本文采用抽头延迟线模型来建模散射信道,每一个抽头对应信号的一个多径分量。
3 系统性能分析
当系统通过散射信道后,会受到多径效应造成的时延扩展和多普勒效应造成的频率偏移的影响,从而产生ISI和ICI[20-21]。接收信号重新表示为:
r(t)=(s(t)*h(t))ej2πεt+n(t),
(7)

(8)
考虑多径时延最大时的影响,令Δ=τL为最大多径时延。解调符号受到多径和多普勒的影响造成时偏和频偏,式(8)可以表示为:
(9)
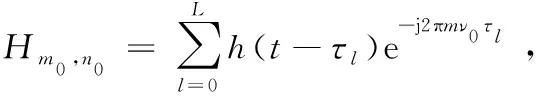
(10)
(11)
从式(11)可以看出,在(m0,n0)处输出信号的有用符号能量为:
(12)
在OQAM/OFDM系统中,使用具有良好的时频聚焦特性的滤波器,符号的干扰主要来自于一阶邻域Ωm,n={am±1,n±1,am±1,n,am,n±1},在(m0,n0)处干扰能量为:
(13)
从式(10)和式(11)可以得到系统的信号干扰比为:
(14)
可以看出,SIR是一个与滤波器性质,子载波间隔和最大时延扩展Δ和频率偏移ε有关的函数。
在一个固定的散射信道中,信道的最大时延扩展,频率偏移和选取的滤波器函数确定时,SIR是一个仅与信号符号周期τ0有关的函数,文献[22]对式(14)进行了近似处理,得到SIR的近似表达式为:
(15)
式中,k1,k2为与滤波器函数有关的系数,当滤波器选为IOTA滤波器时k1=6.4,k2=1.5。
4 仿真分析
本文对OQAM/OFDM系统在散射信道下的信干比进行仿真,在对流层散射通信中,当通信距离为100 km时,信道的多普勒频移小于10 Hz,;当通信距离大于300 km时,最大多普勒频移大于100 Hz。本文在仿真时散射信道模型采用抽头延迟线模型,多径数目为9,最大多普勒频移选取120 Hz,10 Hz,最大时延扩展选取4 μs,0.4 μs。
多普勒频移为10 Hz和时延扩展为0.4 μs时不同滤波器下的SIR曲线如图1所示。从图1中可以看出,随着符号时间的增加,SIR呈现先上升后下降的趋势,SIR存在最优的符号时间。不同的滤波器最优符号时间并不相同,这是由于不同的滤波器时频聚焦特性不同,造成的ISI和ICI也不相同。
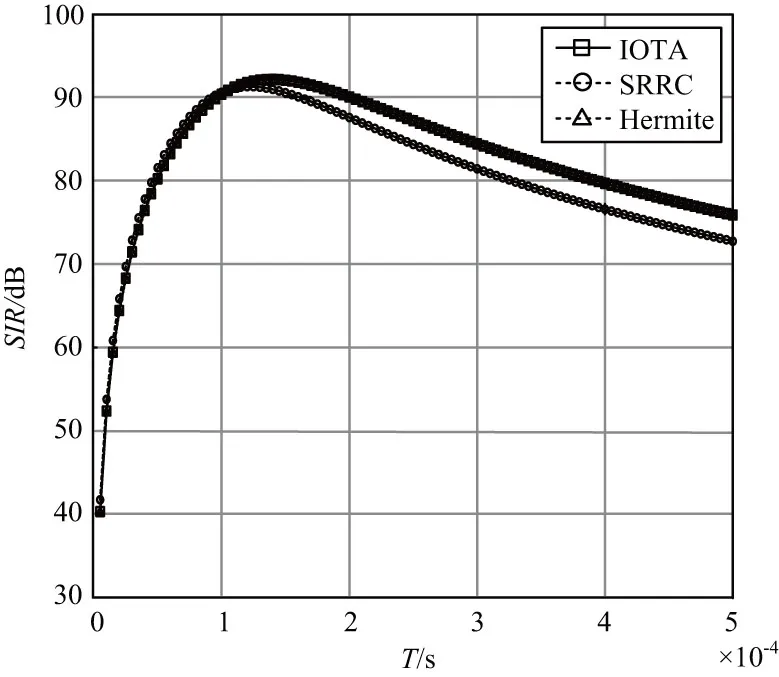
图1 不同滤波器下的SIR曲线
120 Hz频移和4 μs时偏的情况下,SIR随符号时间的变化曲线如图2所示。从图2可以看出,当符号时间较小时,系统的SIR很小,无法满足系统设计的需要。比较图1和图2,随着频移和时偏的增大,系统的SIR明显减小,表明系统性能随着时偏和频移的增大而降低。
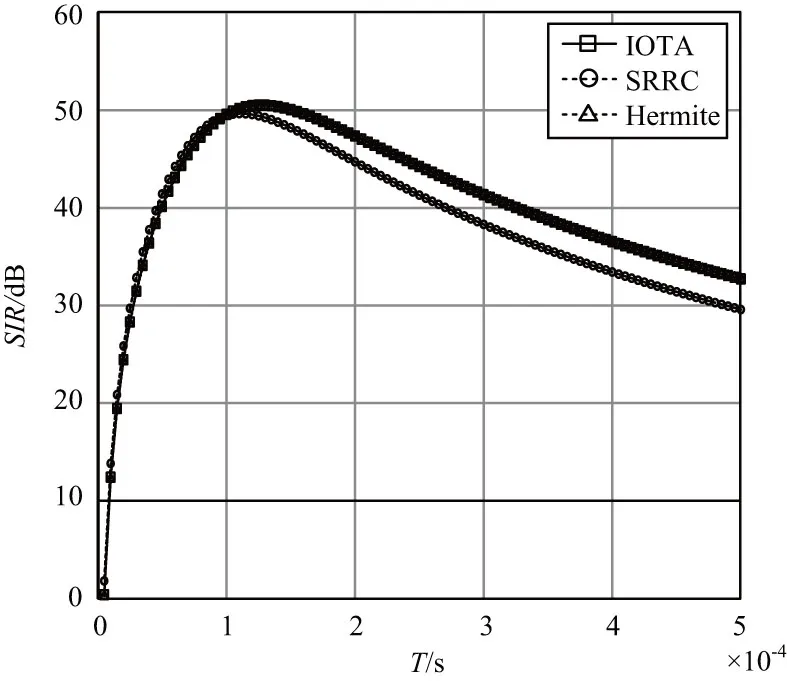
图2 SIR随符号时间的变化曲线
图1和图2展示了2种典型散射信道下OQAM/OFDM系统SIR的性能。从图1和图2可以看出,不同的散射信道下存在最优的符号时间。在散射通信系统中,当通信的发射带宽确定后,可以得到最优的发射子载波数。
5 结束语
本文通过分析OQAM/OFDM系统在对流层散射信道下的ISI和ICI,推导得到SIR公式,通过对不同散射信道下SIR随符号时间的仿真,得到在SIR最大准则下,在不同多普勒频移和时延扩展下有不同的最优符号时间。

