基于几何攻击校正技术的鲁棒水印算法

吴捷

摘要：基于离散小波变换与奇异值分解提出一种新型数字水印算法，其主要目的是提供一种合适的解决方案，以降低几何攻击带来的影响。为了达到该目标，将宿主图像分为4个互不重叠的子图，然后使用DWT-SVD技术分别在其中嵌入水印。水印的冗余可以降低裁剪攻击造成的影响。此外，为了应对诸如旋转、平移等几何攻击，提出一种校正技术，通过边缘检测与对所需图像边角的获取，以重构遭受几何攻击的图像。实验结果表明，与其它水印算法相比，该方案对常见的信号处理与几何攻击都具有较强的鲁棒性。

关键词：离散小波变换;奇异值分解;几何攻击;边缘检测

A Robust Image Watermarking Method Based on a

Technique for Correction of Main Geometric Attacks

WU Jie

（School of Information and Technology， Taizhou Polytechnic College， Taizhou 225300， China）

Abstract：In this article， a new scheme based on a combination of DWT and SVD domains is presented， in which the main focus is to provide proper solutions for reducing effect of geometric attacks. To address this goal， we divide host image into four nonoverlapping rectangular segments called sub images and then watermark is independently embedded into each of them using DWT SVD. The redundancy reduces effect of cropping attack. Moreover， in order to correct main geometric attacks， such as rotation， translation and so on， we propose an inventional correction technique to recover geometrically attacked image via edge detector and detection of desired image corners.Compared with other schemes， the achieved results shows that the proposed scheme has stronger or comparable robustness against common signal processing and geometric attacks.

Key Words：discrete wavelet transform （DWT）; singular value decomposition （SVD）; geometric attack; edge detector

0 引言

數字水印是一种用于图像认证与版权保护的有效方法。数字水印的基本原理是将隐藏的秘密数据生成水印嵌入到原始图像中作为凭证。因此，可以通过检测秘密数据进行数字媒体的版权验证。通常认为，一种有效的水印算法应具有不可感知性与鲁棒性。将对原始图像实施的各种操作称为攻击，主要攻击可分为两大类：①信号处理攻击，如JPEG压缩，以及各类噪声、滤波、模糊等;②几何攻击，如旋转、缩放、剪切、平移等。

数字水印主要是基于空间域或变换域技术实现的。空间域水印算法是通过修改原始图像像素嵌入水印，实现容易且成本较低。相对于空间域技术，如离散小波变换（DWT）、离散余弦变换（DCT）与奇异值分解（SVD）等一系列变换域技术，其在应对信号处理攻击方面更加有效。这是由于其通过修改变换系数嵌入水印，当图像被逆变换时，水印可以不规则地分布在图像上，从而减少了各类图像处理造成的影响。近年来大多数文献也是基于变换域展开的，其中文献[1]选择使用整数小波变换进行信号处理，通过对原始图像进行二级整数小波变换，将低频子带进行分块并根据每一分块的均值与低频子带均值的大小关系得到特征矩阵，最后将该特征矩阵与预处理后的版权信息相结合，构造零水印信息;文献[2]利用果蝇优化算法将离散小波变换（DWT）应用于水印技术中，通过群体智能算法解决水印透明性与鲁棒性之间的矛盾;文献[3]将非下采样变换与奇异值分解相结合，提出一种利用Zernike矩对图像进行几何校正的盲水印算法;文献[4]利用数字全息技术将水印图像生成数字全息图，结合奇异值提出一种具有强鲁棒性的数字水印算法;文献[5]通过对小波逼近子图进行主成分分析（PCA），提出一种基于DWT与感知哈希的零水印算法;文献[6]结合QR分解与Contourlet变换的优点，提出一种新的鲁棒盲水印算法;文献[7] [9]则针对现有算法处理几何攻击鲁棒性不强的问题，提出各自的解决方案。其中，文献[7]、[8]利用SIFT特征点具有的旋转、缩放与平移不变性对几何失真含水印图像进行几何校正，恢复水印的同步性，使算法具备抵抗几何攻击的能力;文献[9]利用SSIM检测并校正图像旋转角度，能有效抵抗1～360°的旋转攻击。

本文基于DWT-SVD技术与几何校正法提出一种新型水印算法，该算法的主要特点是除可以有效应对各种信号处理攻击外，对于诸如裁剪、旋转等几何攻击也具有较强的鲁棒性。

1 几何攻击校正法

为了解决旋转、平移等一系列几何攻击对水印造成的损害，本文提出一种新型的几何校正法。图1（a）是在MATLAB环境中获得的旋转攻击图像。从图中可以看出， 在旋转攻击后，Lena图像周围会产生一些黑色区域，利用该特性可以设法标记出所需的Lena图像边界和顶点。下面以旋转攻击为例阐述本文方法：

（1）首先对旋转后的图像进行Canny边缘检测，得到所需的有效图像。从图1（b）可以看出，Lena图像边界区域被清晰地呈现出来。

（2）对边缘检测后得到的图像应用形态学中的闭操作，该操作可连接间隔细小的断边，得到更清晰且连续的边界。

（3）得到边界之后，接下来的问题则是确定所需图像4个顶点的坐标。顶点位置可通过计算所需图像到外围边界的最小距离加以确定。

例如，图2是对Lena图旋转15°后的图像，根据前3步操作，可以得到Lena图像4个顶点的坐标为（135，1）、（1，494）、（628，135）与（494，628）。

（4） 得到4个顶点后，可以由以下公式计算得出每条边上点的数量：

（5）对于任意一条边而言，设其起点坐标 为（e 1，e 2），终点坐标为（h 1，h 2），则线段上任意点的坐标（p i 1，p i 2）可 由公式（2）计算得到：

至此则获得了所需图像所有点的坐标，可以将每个点的像素值存入另一个矩阵中，得到校正后的图像，用于后期水印的提取。

（a）旋转后的图像 （b）Canny边缘提取

2 水印嵌入与提取

2.1 水印嵌入

本文算法是先將原始图像划分成互不重叠的4幅子图，再对子图进行DWT变换与SVD分解，然后利用加性准则将水印嵌入到LL子带中。原始图像选择256灰度等级（512*512） 的标准图像 I ，二值水印图像大小为64*64。

其步骤可总结如下：

（1）将原始图像 I分为4块，得到256*256的4幅图像，记为SH 1、SH 2、SH 3与SH 4 ，如图2所示。

（2）对 SH 1 进行二层离散小波变换（DWT），得到子带 LL 2作为嵌入区域。

（3）选择 LL 2与水印图像W，对其分别进行奇异值分解，得到[U，S，V]=svd（LL 2），[U w，S w，V w]=svd（W） 。

（4）运用加性准则： Temp=S+αS w（其中α 为嵌入强度因子），修改子带奇异值。

（5）运用公式 LL 2=U×Temp×V′，重构含水印图像的LL 2 系数。

（6）对 LL 2 作两层离散小波逆变换（IDWT），得到含水印的图像 SH * 1。

（7）采用同样方法，可以获得含水印的图像 SH * 2、SH * 3与SH * 4 。

（8）将图像 SH * 1、SH * 2、SH * 3与SH * 4合并得到完整图像I * 。

2.2 水印提取

本文算法在提取水印时需要使用原始图像，具体步骤如下：

（1）将待测图像 I *进行分块，得到SH * 1、SH * 2、SH * 3与SH * 4 。

（2）对 SH * 1 进行两层离散小波变换（DWT），得到子带 LL * 2 。

（3）对 LL * 2进行奇异值分解，得到[U 2，S 2，V 2]=svd（LL、+* 2）。

（4）运用公式 S * w=（S 2-S）/α提取水印（其中α 为嵌入强度），得到要提取水印的奇异值矩阵。

（5）运用公式 W * 1=U w×S * w×V w 重构水印图像。

（6）同理可以分别提取出嵌入在 SH＼+* 2、SH * 3与SH * 4中的水印W * 2、W * 3和W * 4 。

（7）使用公式 W N=（W * 1+W * 2+W * 3+W * 4 ）/4计算平均水印，并根据公式（3）得到最终水印。

W N（i，j）=0 If W N（i，j）<0.5

3 实验结果与分析

本文实验环境采用软件为Matlab7.0，为了使实验结果更有说服力，采用Lena、Boat、Peppers、Baboon 共4幅512*512的标准灰度图像作为测试图像，水印图像采用64*64的二值图像——“苏州大学”，并采用峰值信噪比PSNR作为图像质量评价标准。为了验证本文算法的鲁棒性，本文使用的方法是计算提取出的水印 W N与原始水印W 之间的相似度NC值，并与相关文献进行比较。

表1中给出的是在未经任何攻击的情况下，从4幅测试图像中提取出的水印参数，其中NC值为1，PSNR值均在58以上，说明利用本文算法嵌入的水印具有不可见性，并且可以被正确提取。

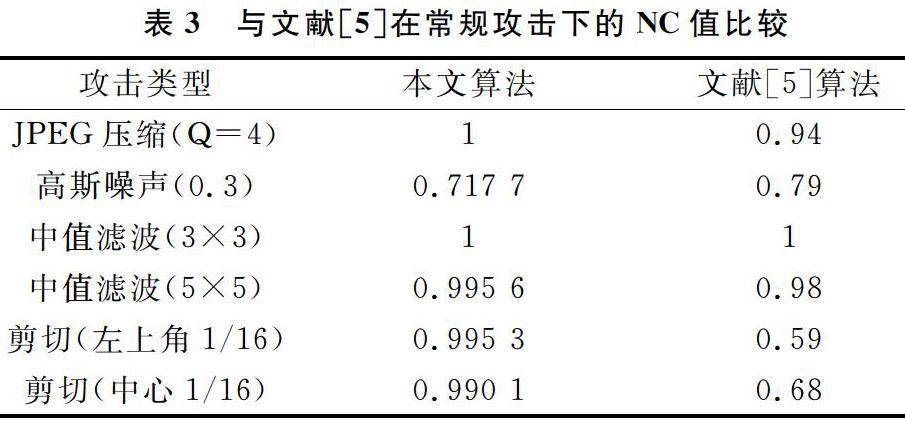
表2-表4是本文算法与文献[2]、[5]、[7]算法的比较。文献[2]使用的测试载体图像与本文相同，使用的水印“中国南沙”也与本文基本一致。表2列出了几种常见攻击的实验数据，可以看出，本文算法的鲁棒性要强于文献[2]的算法;文献[5]测试载体图像使用256*256的Lena图像，水印使用64*64的二值图像“HN”。表3列出部分对比数据，除高斯噪声攻击外，本文算法的测试数据优于文献[5]的算法。值得注意的是，本文算法应对裁剪攻击非常有效，主要因为本文算法在4幅子图中都嵌入了水印，裁剪其中一部分对测试结果影响不大;文献[7]同样使用512*512的Lena图像作为测试载体图像，水印使用32*32的二值图像“CS”。本文算法加入水印后，图像的PSNR值为58.847 4，略高于文献[7]。由表4可以看出，除高斯滤波攻击外，本文算法在各种攻击下的表现都优于文献[7]的算法。

现有研究在处理旋转攻击时，大都是针对“crop”参数（裁剪初始测试图像，保持整个图像框大小不变）进行的，而针对“loose”参数（不裁剪初始测试图像，相应放大整个图像框）的研究并不多。研究如何应对后一种攻击方式也具有较高的实际应用价值，本文与文献[20]即是针对这一类旋转攻击开展研究的。图3给出了本文与文献[20]针对不同旋转度数攻击计算出的NC值。可以看出，本文算法在任何旋转度数攻击下都有稳定的测试数值，优于文献[20]的算法。

图4则给出了左上角剪切1/16、中心剪切1/16、左上角剪切1/4、中心剪切1/4、任意剪切5种情况下的NC值柱状图，可以看出本文算法对各种剪切攻击都具有较强的鲁棒性。

图5（a） 为含水印图像及未受任何攻击下提取出的水印图像。图5（b）-（h）分别给出了常规攻击下含水印图像及提取出的水印，可以看出提取出的水印辨识度较高，说明了本文算法的有效性。

4 结语

本文基于小波变换、奇异值分解与几何校正法，提出一种新型数字水印算法。与之前算法最大的不同在于，水印是独立嵌入在4个不同子图中，另外本文针对诸如旋转、平移等几何攻击采用提取边缘、计算顶点坐标的方法，以恢复原始图像。根据大量实验结果以及与其它算法的比较，证明本文算法不仅能够有效抵抗信号处理攻击，而且对于几何攻击也有很好的鲁棒性。将来主要工作在于进一步提高图像边缘提取的准确性，并研究更加有效的方法实现水印嵌入。

参考文献：

[1] 曾文权，熊祥光.基于整数小波变换的鲁棒零水印算法[J].微电子学与计算机，2016，33（4）：97 101.

[2] 肖振久，孙健，王永滨，等.基于果蝇优化算法的小波域数字水印算法[J].计算机应用，2015，35（9）：2527 2530.

[3] 陈盈，郑洪源，丁秋林.基于Zernike矩和NSCT SVD的数字水印算法研究[J].计算机科学，2016，43（8）：84 88.

[4] 王祖喜，毛刘刚，胡汉平.基于数字全息和奇异值分解的鲁棒性数字水印方案[J].小型微型计算机系统，2014，35（8）：1789 1793.

[5] 徐莲，李京兵.基于DWT PCA 和感知哈希的鲁棒零水印算法[J].电视技术，2016，40（1）：25 30.

[6] 刘海，陈军.基于QR分解的Contourlet域鲁棒盲水印算法[J].计算机应用与软件，2016，33（6）：306 310.

[7] 贾超，张政保.基于改进SIFT 的抗几何攻击水印算法[J].小型微型计算机系统，2014，35（12）：2655 2658.

[8] 严敏，陈军.基于QR分解的Contourlet域抗几何攻击水印算法[J].计算机应用研究，2016，33（9）：2813 2818.

[9] 廖斌，任美玲，徐俊刚.抗任意旋转攻击的数字水印防伪技术[J].光电子·激光，2015，26（1）：156 161.

[10] 张勤，崔丽.基于DWT的一種数字水印算法[J].北京师范大学学报：自然科学版，2015，51（1）：19 22.

[11] 王勇.奇异值分解小波变换的数字水印算法研究[J].计算机仿真，2011，28（5）：295 298.

[12] 薛胜男，陈秀宏.基于混沌加密和SVD的数字图像水印算法[J].计算机工程，2012，38（19）：107 110.

[13] 李莹，李春兴，于晓.一种基于DCT鲁棒性的数字水印算法[J].青岛科技大学学报：自然科学版，2015，36（4）：443 448.

[14] 徐慕蓉，樊锁海.一种新的基于奇异值分解的图像数字水印算法[J].计算机仿真，2011，28（5）：291 294.

[15] 叶闯，沈益青，李豪.基于人类视觉特性（HVS）的离散小波变换（DWT）数字水印算法[J].浙江大学学报：理学版，2013，40（2）：152 155.

[16] 贾朱植，祝洪宇，程万胜.基于提升小波变换的自适应盲水印算法[J].计算机工程，2011，37（2）：143 147.

[17] 季燕.基于DCT的自适应盲数字水印[J].计算机科学，2013，40（7）：129 131.

[18] 叶双清，杨晓梅.基于小波变换和非局部平均的超分辨率图像重建[J].计算机应用，2014，34（4）：1182 1186.

[19] 杨勇，郭吉强.Lipschitz指数与平稳小波变换在CT图像去噪中的应用[J].计算机工程与应用，2012，48（6）：190 192.

[20] LI J， ZHU Y. A geometric robust image watermarking scheme based on DWT SVD and Zernike moments[C].IEEE International Conference on Computer Science and Information Technology. IEEE， 2010：367-371.