职工心理健康卫生状况的评价

鲁晓晓，王子延

（1.96863部队，洛阳 471003；2.火箭军工程大学，西安 710025）

1 职工心理健康评价模型

1.1 模型的建立

通过分析数据预处理得到的数据，得到每个人10项指标下属的各个小题中分值分别为2、3、4、5的项目数，（我们认为1分项目对职工心理不健康的贡献度为0，故不纳入模型。）其对应评价标准为比较好，一般，比较不好，很不好。各项目个数记为cij，i为人物编号，j为分数项目（j=2,3,4,5）。需要建立职工心理健康的评价模型，首先考虑运用层次分析法建模。

首先，将心理是否健康分为三个层次，即为：

目标层：确定某人是否健康

准测层：10个影响指标

数据层：各影响指标下属各题目的分值

其次，确定各层次互相比较的方法——成对比较矩阵和权向量；

本文利用专家经验推断法，对职工心理是否健康给予以下标准判定确定：5分题对调查者是否健康的重要性为 7；4分为5；3分为 3；2分为 1。

图1 确认健康的目标层和准则层

用于比较第三层的四种元素对上一层因素的影响所采用的方法是：首先随机取两个元素，然后比较它们对目标因素的影响，并用aij表示，比较的结果用成对的比较矩阵表示，即：

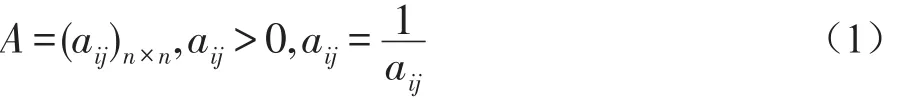
依据上述比较矩阵，本问题中的成对比较矩阵为：

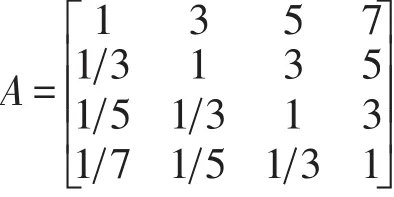
通过该矩阵，可以发现在上述矩阵中各元素存在不一致性，所以在对其进行成对比较出现了不一致的情况下，计算各因素C1,C2,C3,C4对上层因素的权重，并确定出现的这种不一致所允许的误差范围。因而需要进行一致性检验.其一致性指标为：

具有如下性质：

当λmax=n时，有：C·I=0，Aˉ为完全一致性,C·I值越大，主观可以判断矩阵A的完全一致性越差，即：偏离A越远。

一般地，若C·I＜=0.1，则认为主观判断矩阵的一致性是可以接受的，否则应重新进行相互比较，构造另外的主观判断矩阵。

随机进行一致性的检验指标：通过实际检验，主观判断矩阵的维数越大，判断的一致性将越差，因此放宽对高维矩阵的一致性要求，于是引入修正R·I，用来校正一致性的检验指标，如表1所示：

表1 随机一致性检验指修正值表

一致性比率C·R=C·I/R·I。若C·R＜0.1，则认为主观判断矩阵的不一致程度在允许的范围之内，可用其特征向量作为权向量；否则，将对主观判断矩阵进行重新成对并比较，构成新的主观判断矩阵。

1.2 模型的求解

利用MATLAB软件eig函数算出矩阵A的最大特征值为：

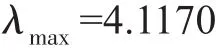
一致性指标为：

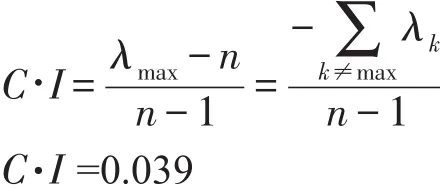
特征向量为：

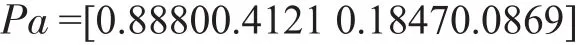
一致性检验有C·R=0.043876＜0.96，故认为满足一致性要求。

权重为特征向量归一化作为4个准则对应目标的权重

（x5,x4,x3,x2）=（0.55789,0.26335,0.12187,0.05689）

然后利用各项目个数cij，i为人物编号，j为分数项目（j=2,3,4,5），乘以相应的权值xi得到总分：

因为每个因素对应的问题数目不同，所以其总分也不同。为此我们分别定义各个因素的心理健康程度区间如表2。

利用上述模型求得每个人各项的分数，然后利用Excel的筛选，筛选出各项中心理疾病比较严重的人如表3所示。

表2 各项指标评价分类

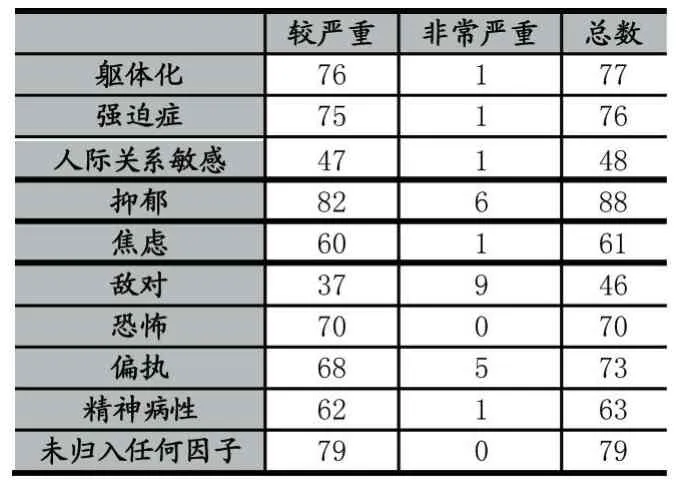
表3 各项指标计算结果（n=1214）

然后我们利用参考文献中提到比较平均值的比较方法在对原始数据进行计算得到题中所给数值的均值结果如表4所示。

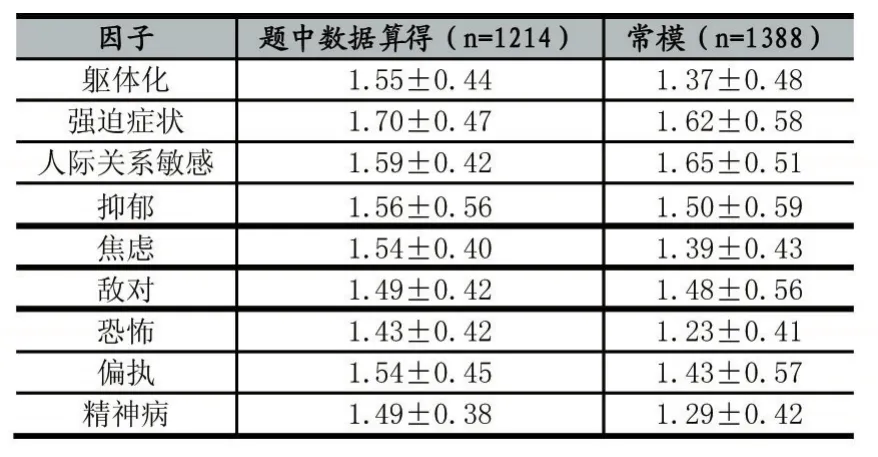
表4 平均分与常模的比较

由表4可以看出，如果仅仅通过平均值来与常模比较，大部分指标都与常模相差甚远，得到的结果为大部分人都是心理不健康，故此方法不科学。而我们则将各项因子对于最终结果的权值考虑在内，纳入结果的计算中，得出1214人中仅大约6%的人存在心理疾病，这样的结果更为合理，更有说服力。

2 职工心理健康主要影响因素

本问题需要进一步分析影响职工心理健康的因素，并得到各因素与心理健康的关联程度。首先，我们对职工不同的性别、工龄、是否是独生子女、类别、学历、家庭结构、对公司的适应程度、公司管理方式、人际交往的情况以及上级领导的态度对于职工心理健康的影响利用独立样本T检验作出了比较。

2.1 两独立样本 T检验[1]

（1）提出假设

两个独立样本T的检验需要检验两个总体样本均值是否存在显著性差异。

假设H0：μ1=μ2，这里，u1和u2分别为两个总体样本的均值。

例如，检验两所院校的英语平均成绩是否相等，其零假设为H0：μ1=μ2

（2）选择检验统计量

两个独立样本均值进行假设检验的前提，是两个独立的总体分别服从分别为两个总体样本的方差。

在假设成立的条件下，两个独立样本的均值假设检验均使用t统计量。构造两个独立样本的t统计量时，必须考虑以下两种情况：

这里，n1、n2分别为两样本容量；S1、S2分别为两样本标准差，且，这个统计量的自由度为n1+n2-2，并且它为t分布。

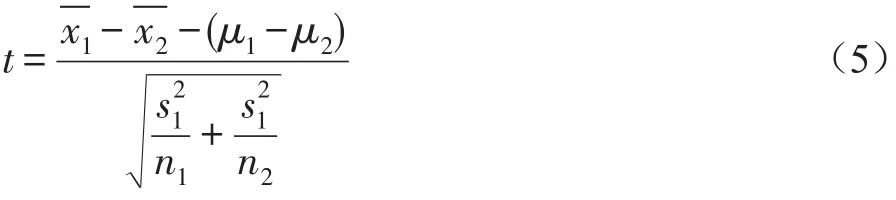
实践表明，这个检验统计量为修正自由度后的t分布，它的修正自由度是：

在统计学领域，有两个变量且它们的方差相等，我们就说它们满足方差齐性。如果我们想构造和选择两个独立的样本T检验，它的关键是两独立样本的方差齐性。我们利用的SPSS软件，它是选择Levene F方差齐性检验方法，观察两总体方差，看它们是否存在显著差异。

F检验中，计算F统计量值的公式是：

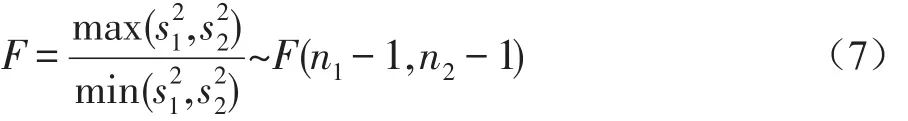
这里n1-1为的自由度，n2-1为的自由度。

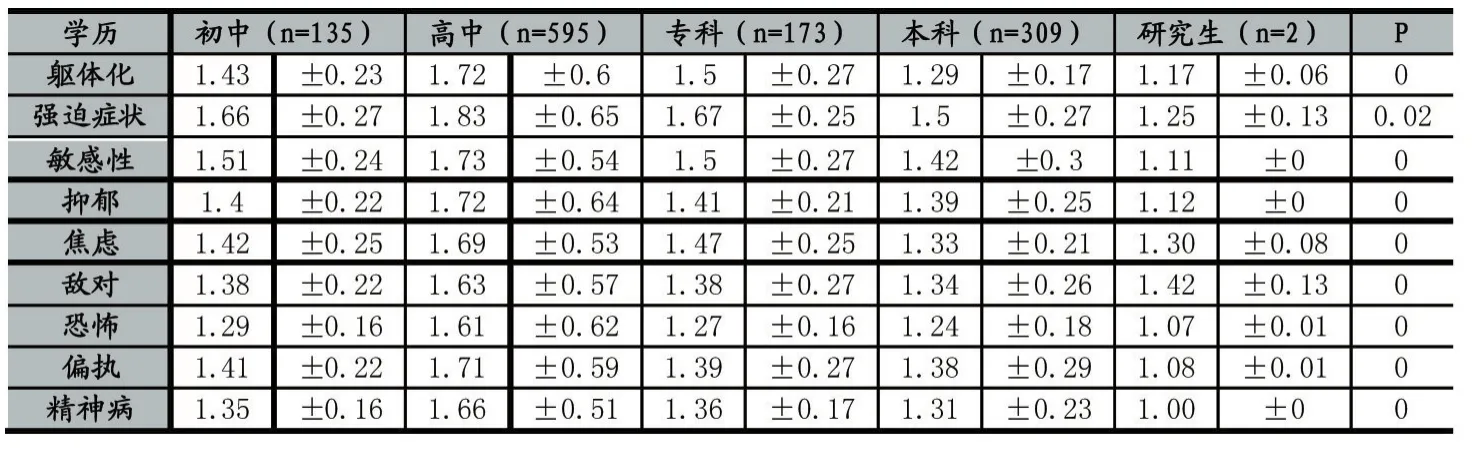
表5 学历对心理影响T检验结果

（3）计算检验统计量的观测值和发生的概率

假如零假设已经给定，利用SPSS统计计算，将检验值0带入t统计量的μ1-μ2部分，从而计算出检验统计量的观测值并且我们还可以从t分布函数计算出概率p的值。

假如概率值p小于给定的显著性水平，则认为假设H0不成立，认为总体的平均值与μ0存在较大的差异；反过来，如果大于给定的显著性水平，则认为两者的差异性不大。

利用上述模型统计过的数据进行处理得到结果。

由于将全部结果表格至于论文中，论文过于凌乱，所以我们进将两个具有代表性表5、表6的给出。

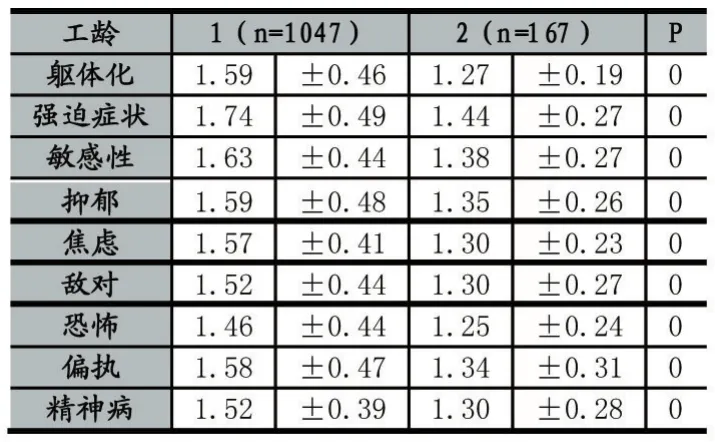
表6 工龄对心理影响T检验结果

对上述的表进行分析得到如下结果：

由表5可以看出，p＜0.05,所以学历差别对于9个因子的影响都很大。

由表6可以看出，p＜0.05,工龄差别对于9个因子的影响都很大。

与学历和工龄差别同理，求取公司的管理方式、是否是独生子、家庭结构、职工类别、上级领导的态度、能否适应公司的生活、人际交往的情况、性别、家庭教养的p值，得到对于职工心理健康有影响的因素为：是否是独生子、职工类别的不同、上级领导的态度、能否适应公司的生活、人际交往的情况。

综上所述，可知工龄、是否为独生子女、上级态度、学历、人际关系以及对公司的适应程度与职工心理健康相关性很大，而职工类别则相对小一些，性别、家庭结构、家庭教育方式、公司管理模式则与职工心理健康相关性不大。故总结影响职工心理的主要因素有工龄、是否为独生子女、上级态度、学历、人际关系以及对公司的适应程度。

2.2 灰色关联度的建模及求解

针对问题二中家庭教养方式、公司环境、公司管理模式、上级领导的工作态度与职工心理健康的关联程度，我们采用灰色关联度的方法[2]进行统计分析。分析步骤如下：

①先找到整体的参考数组和比较数组。用于表现整体行为特征的数组，称为参考数组。而影响整体因素组成的数组，称为比较数组。

②因为整体中各个因素的数据量纲并不一样，并不能用来比较，所以数据分析之前，我们首先进行无量纲化处理。

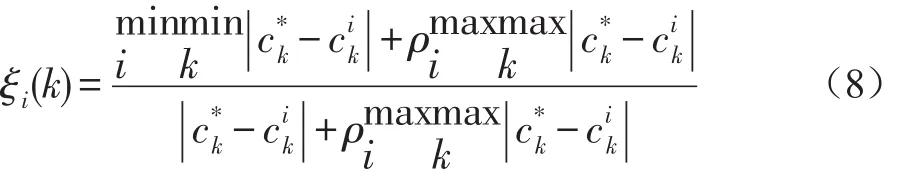
式中ρ=（0,1）,一般取ρ=0.5

④计算关联度ri

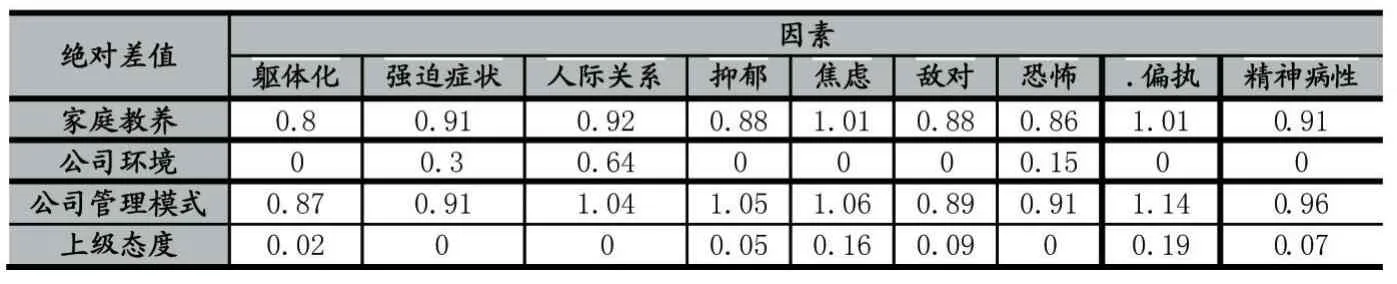
表7 绝对差值

表8 相关系数

表9 各量值对应权值

如第i个被评价对象的关联度ri最大，说明与最优指标最接近，即第i个被评价对象比其他被评价对象更好，那么我们就可以排列出每个被评价对象的先后顺序。

采用灰色关联度分析方法评价各种因素与心理健康的相关程度。

第一步：数据分析，通过上面问题分析得到家庭教养方式、公司环境、公司管理模式、上级领导的工作态度的均值，由上文可知均值差异越大，该因素与职工心理健康关系越大，所以将各个因素中两两取差值的绝对值相加得到评价矩阵：

第二步：无量纲化处理，因为我们的数据为均值之差，量纲相同。

第三步：利用公式（8）计算灰色关联系数，计算结果如表8。

利用分层分析法计算出各量值的权值如表9。

计算出家庭教养、公司环境、公司管理模及式上级态度的关联如表10所示。

从图2可看出等权和加权后，公司环境和上级态度都为主要影响因素，故我们得到第二问结果公司环境和上级态度与职工心理健康程度相关程度较大，而家庭教养方式和公司管理模式则较小。

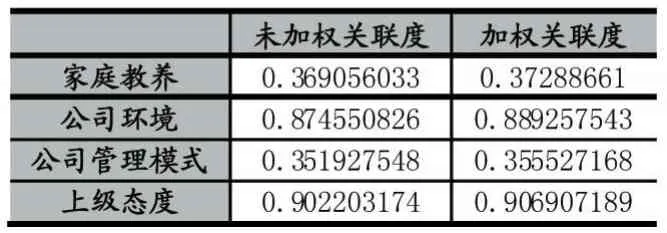
表10 各方面关联度

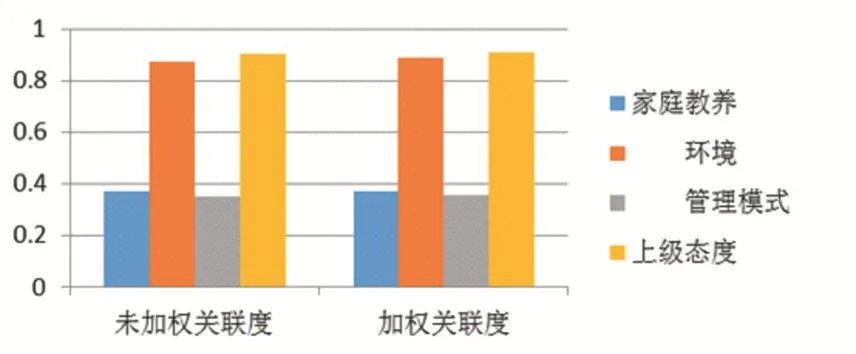
图2 加权前后关联度对比图

3 讨论

模型优点：

（1）本文综合考虑了各种心理影响因素，分析较为全面，其次采用关联度分析，结论可靠。

（2）模型可拓展性强。模型按照决策变量、目标函数、限制条件三个大模块构建，每一个大模块又分为几个小模块。当新情况出现时，无需重新建立模型，只需在已有模型基础上进行再规划，适当增加约束条件、修改目标函数，即可求解新条件下的规划方案。

不足之处：

（1）模型采用的方法为主观加权法，考虑不周全。

（2）本文中只分析出产生的原因，并没有给出解决方法。

[1]张庆利.SPSS宝典.电子工业出版社，2011.2.

[2]司守奎，孙玺箐.数学建模算法与应用.国防大学出版社，2013.2.

[3]王家华等.中国新兵SCL-90常模的建立[J].中国心理卫生杂志，2000，14（4）.

[4]（英）查尔斯·杰克逊.了解心理测验过程.北京大学出版社，2000.3.