基于虚拟同步电机的负荷换流器建模及参数设计
何光辉, 张仰飞, 陈光宇,袁宇波, 张宸宇, 史明明
( 1. 南京工程学院电力工程学院,江苏 南京 211167;2. 国网江苏省电力有限公司电力科学研究院,江苏 南京 211103)
0 引言
近几年,随着新能源发电设备不断接入电网,电网逐步发展为以电力电子换流器为主导的低惯量、欠阻尼网络,电网的稳定性和安全性问题越来越突出[1]。当前研究的重点是面向分布式电源,通过构建虚拟同步发电机,使含有电力电子换流器的分布式电源模拟传统同步发电机的运行特性,为系统稳定性提供支撑作用。然而,随着电力电子技术的不断发展,大量的负荷换流器也不断接入电网中。仅通过分布式电源模拟同步发电机已不足以支撑越来越庞大的电网安全稳定运行,必须从负荷侧入手,使负荷换流器同样模拟传统同步电机的运行特性,参与电力系统调频、调压过程,提高系统的稳定性,实现源-网-荷的高效运行[2]。
由于虚拟同步电机技术[3-6]使换流器模拟传统同步电机特性,因此对电网天然友好,受到国内外学者广泛关注。文献[7]提出一种电动汽车快充方案,为从负荷侧支撑系统稳定提供了一种思路,但电网的波动对负荷如何影响没有介绍。文献[8]提出一种能量路由器电路,由于主动降低负荷电压,损害了负荷侧的利益。文献[9]提出一种基于虚拟同步电动机技术的变频器控制策略,能够使变频器模拟虚拟同步电动机的特性,但其控制参数如何设计没有阐述。文献[10—13]介绍了几种传统负荷换流器控制方法,但是当电网电压波动时,负荷无功不变,不支撑电网的电压稳定。为此,文中针对负荷换流器,提出一种基于虚拟同步电机的负荷换流器控制模型及控制参数设计方法,为从负荷侧解决电网稳定问题提供思路。搭建了负荷虚拟同步电机的Matlab/Simulink仿真模型并进行了仿真,仿真结果验证了所提方法的可行性和有效性。
1 系统结构
负荷虚拟同步电机通过利用虚拟同步电机技术控制负荷换流器来模拟传统同步电机的工作状况,从而表现出传统同步电机的运行特性。其基本结构如图1 所示。
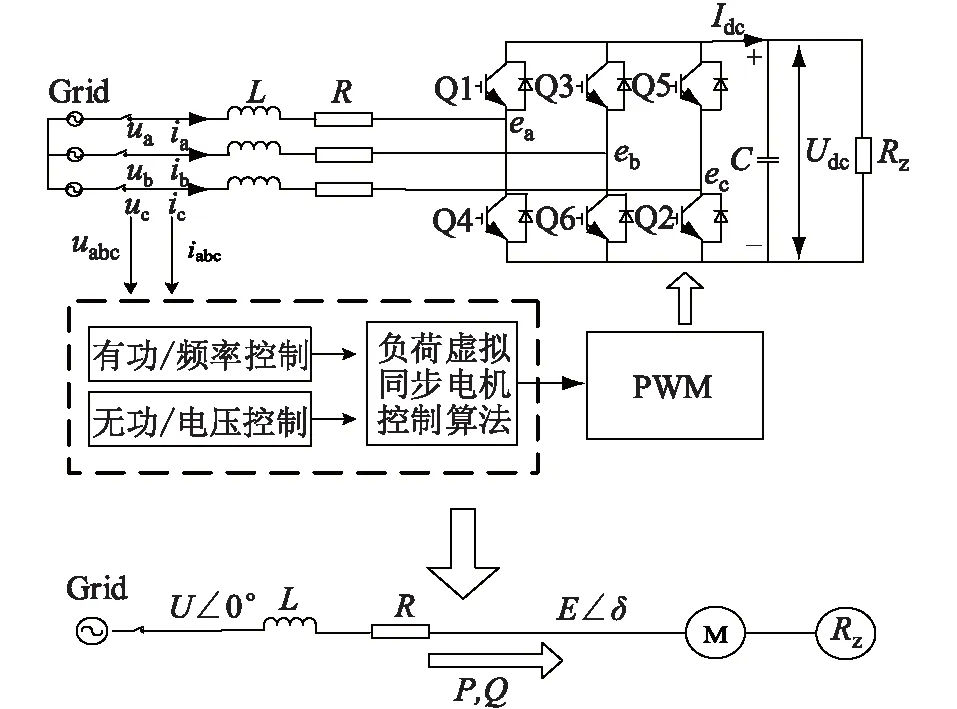
图1 负荷虚拟同步电机的原理Fig. 1 Schematic diagram of VSM
其中,Q1—Q6组成三相整流桥,Rz为负荷换流器内阻。控制部分主要由功率控制和负荷虚拟同步电机算法组成,功率控制包含有功-频率控制、无功-电压控制。负荷虚拟同步电机将测得的端电压uabc和端电流iabc经过功率控制环节,送入负荷虚拟同步电机控制算法中,得到相应的控制信号。将控制信号通过脉宽调制(pulse width modulation,PWM)送回到换流器中,使得直流侧输出电压为设定值。
2 控制策略
负荷虚拟同步电机的数学模型可以用经典二阶模型来进行描述[14]。与电源侧虚拟同步发电机不同的地方在于,负荷虚拟同步电机的电流方向与电源侧虚拟同步发电机电流方向相反,即由交流电网侧流向直流侧。
设定负荷虚拟同步电机的极对数为1,其机械方程:
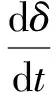
(1)
(2)
式中:δ为负荷虚拟同步电机的功角;ω为负荷虚拟同步电机的角频率;D为阻尼系数;J为负荷虚拟同步电机的转动惯量;Tm,Te和Td分别为负荷虚拟同步电机的机械转矩、电磁转矩和阻尼转矩;ω0为电网额定角频率。
其电磁方程:
(3)
式中:eabc为负荷虚拟同步电机的内电势;uabc为负荷虚拟同步电机的端电压;L和R分别等效为负荷虚拟同步电机的定子电感和定子绕组,分别对应交流接口处的滤波电感及其寄生电阻。
负荷虚拟同步电机的有功-频率控制框图如图2所示。在有功-频率控制中,负荷侧测得的直流电压Udc与直流参考电压Udcref相比较后,进行PI控制,然后将PI控制器的输出结果与直流侧电压参考值相乘,可以得到有功功率的参考值Pref。
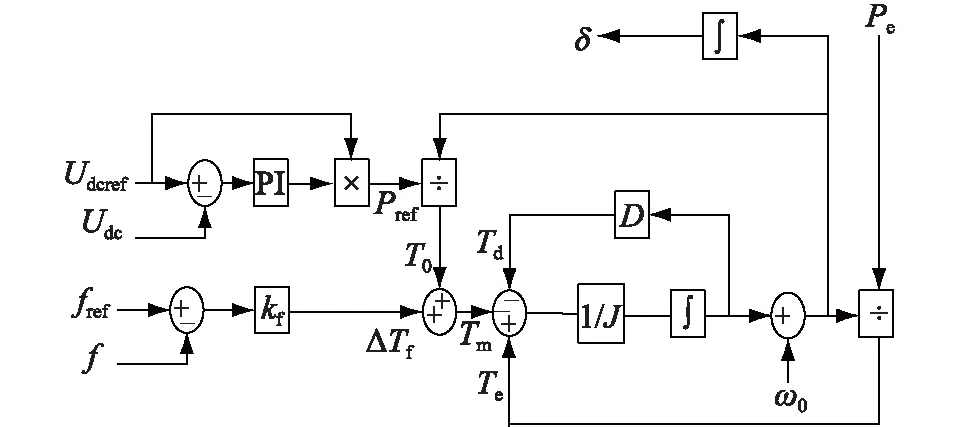
图2 负荷虚拟同步电机有功和频率控制Fig.2 Active and frequency control diagram of VSM
负荷虚拟同步电机的机械转矩Tm由额定转矩指令T0和频率调节的部分ΔTf组成,可表示为:
Tm=T0+ΔTf
(4)
式(4)中额定转矩指令T0=Pref/ω,频率调节的部分ΔTf=kf(f-fref)。其中,kf为频率调节系数;f为负荷虚拟同步电机的频率;fref为电网额定频率。
负荷虚拟同步电机的电磁功率由内电势eabc和端电流iabc得出,表示为:
Pe=eaia+ebib+ecic
(5)
电磁转矩由电磁功率与负荷虚拟同步电机的角频率得到,表示为:
(6)
负荷虚拟同步电机无功-电压控制框图如图3所示。
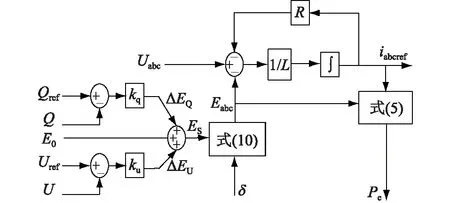
图3 负荷虚拟同步电机无功和电压控制Fig.3 Reactive power and voltage control diagram of VSM
在无功-电压控制中,负荷虚拟同步电机的无功功率可得:
(7)
负荷虚拟同步电机的内电势指令由电机的空载电势E0、无功调节的部分ΔEQ以及电压调节的部分ΔEU组成,可以表示为:
ES=ΔEQ+E0+ΔEU
(8)
其中无功调节的部分ΔEQ和电压调节的部分ΔEU分别表示为:
(9)
式中:kq,ku分别为无功、电压调节系数;Qref和Q分别为交流接口处的无功指令和瞬时无功;Uref和U分别为负荷虚拟同步电机的端电压指令以及真实值。可以得到虚拟同步电机的虚拟电势矢量:
(10)
可以看出,图2、图3所示的控制框图中,包含了传统同步电机的机械方程和电磁方程。因此,该控制可将负荷换流器模拟成传统同步电机来控制,构成了负荷虚拟同步电机。
3 小信号模型
负荷虚拟同步电机与电网交换的功率可以表示为:
(11)
式中:Ug为交流电网相电压;E为负荷换流器交流侧相电压;δ为Ug和E的相位差;X为滤波电路总电抗。
当负荷虚拟同步电机在稳态工作状态下发生小扰动时,可认为sinδ≈δ,可得到电磁功率小信号表达式:
(12)
由式(12)及图(2)可得到有功控制环的小信号控制框图如图4所示。
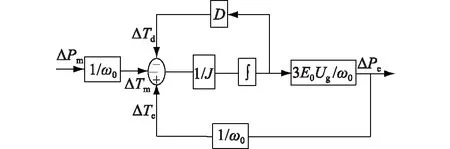
图4 有功控制环的小信号控制Fig.4 Small signal control diagram of active control
根据功率守恒原则,当忽略负荷换流器内部功率损耗时,换流器直流侧功率应与交流侧功率相等。再根据基尔霍夫电流定律,则有:
(13)
又由负荷虚拟同步电机的电磁功率Pe=EI,可得电磁功率Pe与直流侧电压Udc的小信号模型:
(14)
由式(14)和图2可得到负荷虚拟同步电机的小信号控制框图,如图5所示。
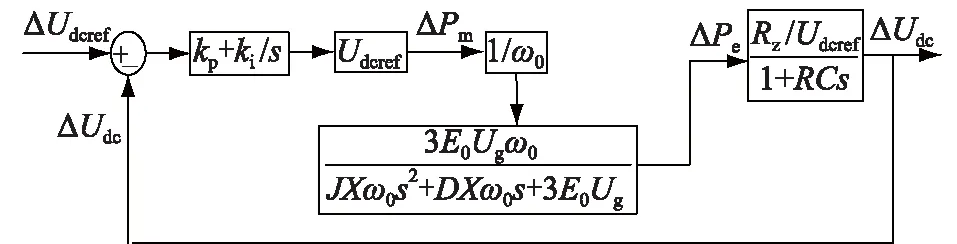
图5 负荷虚拟同步电机小信号控制Fig.5 Small signal control diagram of VSM
由图5所示的小信号模型,可得负荷虚拟同步电机的开环传递函数为:
(15)
4 控制参数设计
可将式(15)所示的负荷虚拟同步电机的开环传递函数化简为:
(16)
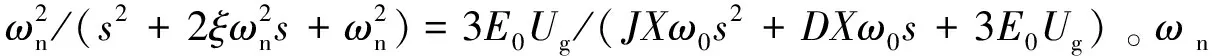
自然振荡频率ωn和阻尼比ζ分别为:
(17)
可得,
(18)
为了兼顾系统的阻尼效果和动态响应性能,工程上阻尼比ζ一般取在最佳阻尼比左右,文中取阻尼比ζ=0.707。
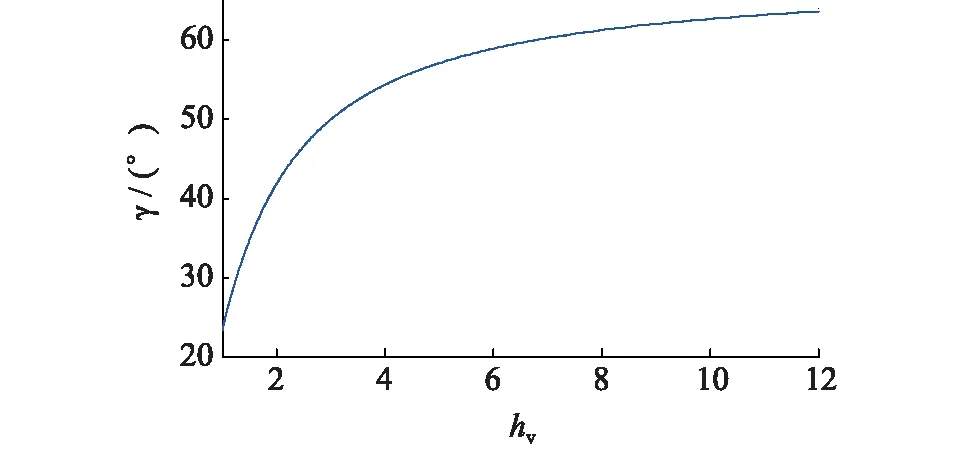
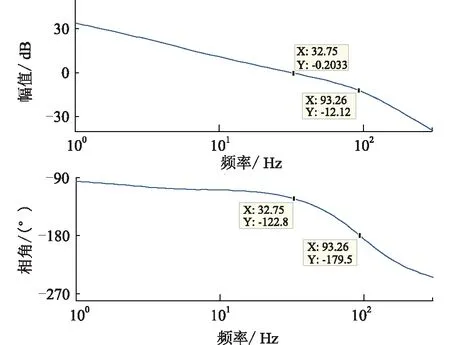
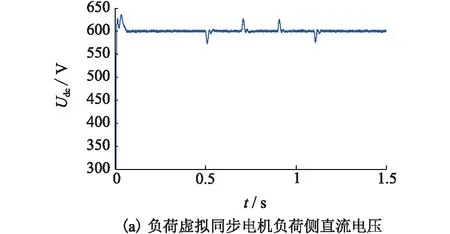
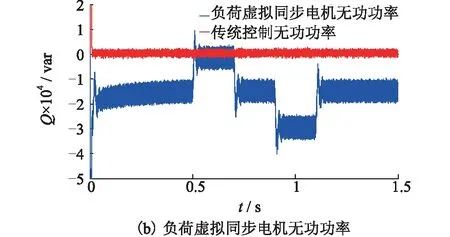
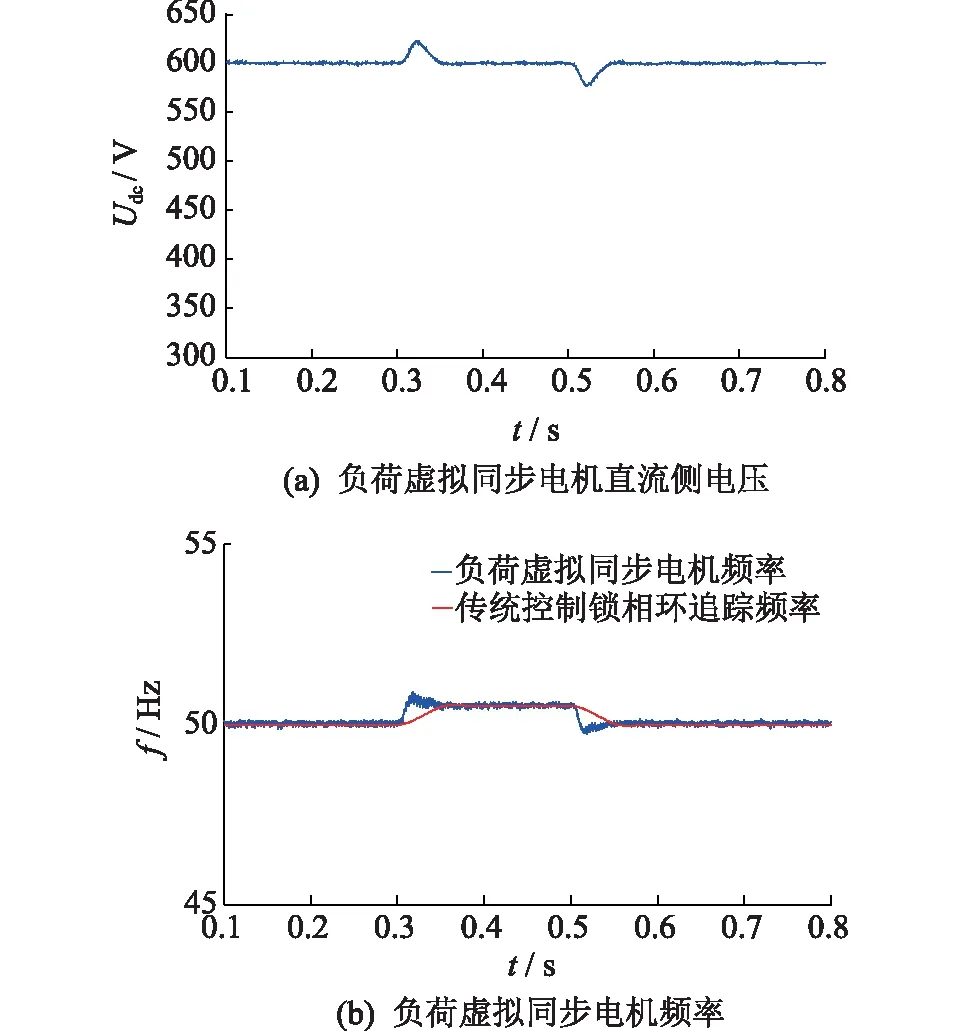
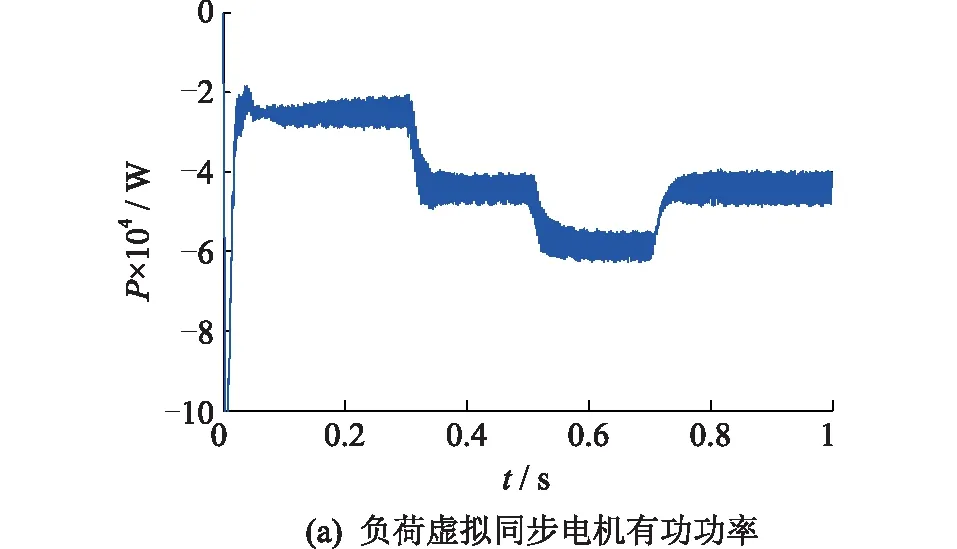
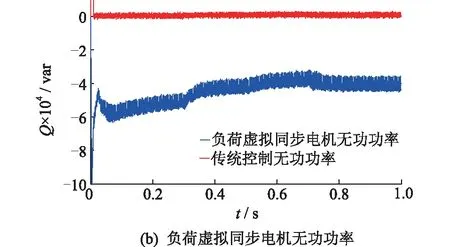
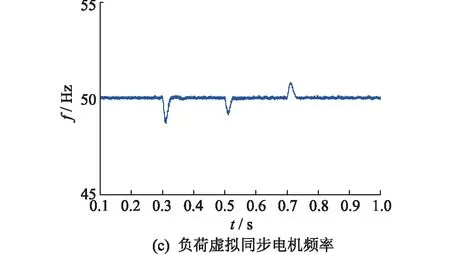
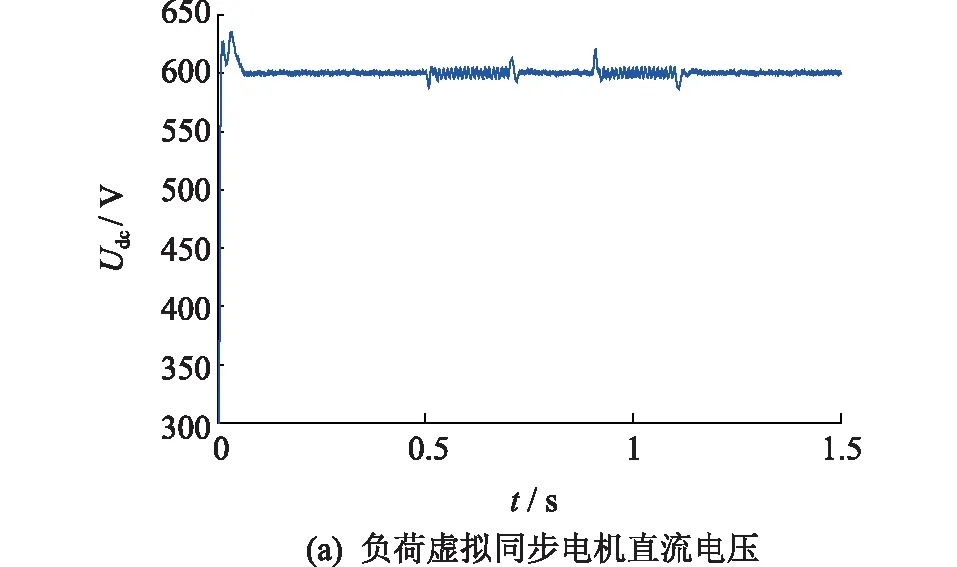
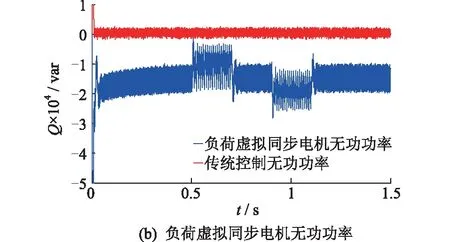
幅频特性曲线的低频段负斜率越大,位置越高,则闭环系统在满足稳定条件时的稳态精度越好。并且,高频段的特性分贝值越低,系统的抗干扰能力越强。因此,为了保证负荷虚拟同步电机的稳定性,开环传递函数的截止频率ωc应该处于幅频特性曲线的-20 dB斜率段[15]。图6给出了负荷虚拟同步电机的开环幅频特性曲线,其中1/RzC 图6 负荷虚拟同步电机开环幅频特性曲线Fig.6 Open-loop amplitude-frequency characteristic curve of VSM 由图6可知,当J取值过大时,二阶振荡环节的自然振荡频率ωn会和一阶微分环节的转折频率ki/kp十分接近,从而开环截止频率ωc会十分接近一阶微分环节的转折频率,这样就会导致系统的相角稳定裕度大幅度降低,不利于系统的稳定。为了减小谐波对二阶振荡环节的影响,截止频率ωc应该小于2倍工频,文中取ωc=200 rad/s。由于负荷虚拟同步电机的二阶自然振荡频率ωn需要满足ωc<ωn的条件,可取ωn=585 rad/s。 在截止频率ωc处,系统开环传递函数幅频特性 A(ωc)= (19) 其中hv=ωc/(ki/kp),表征一阶微分环节的转折频率ki/kp与截止频率ωc的相对大小。 此处,系统相角裕度γ表示为: (20) 为了兼顾系统的稳定性和快速性,系统的相角裕度γ通常要满足30°≤γ≤70°[16-17]。图7给出了hv与系统相角裕度γ的关系曲线。由图7可知,当hv取值过小时,hv的微小变化即可对系统的相角裕度产生过于明显的变化。当hv取值过大时,hv的变化不能有效的影响系统相角裕度。文中取hv=5,此时hv的变化对系统相角裕度的影响适中,易于控制。 图7 hv与系统的相角裕度γ关系曲线Fig.7 Relationship graph between hv and angle margin γ 因此,可得到控制参数的计算表达式如下: kp=kihv/ωc (21) (22) 为验证文中所提出的基于虚拟同步电机的负荷换流器小信号模型及控制参数设计方法的可行性和有效性,在Matlab/Simulink中搭建了图1所示结构的模型进行仿真验证。负荷虚拟同步电机控制方法的参数如表1所示。 表1 负荷虚拟同步电机系统参数Tab.1 Parameters of VSM 由上面已知参数,根据式(18)可计算负荷虚拟同步电机的转动惯量J=0.001 7,阻尼系数D=6;再根据式(21)可计算的有功控制环节PI控制器的比例系数kp=0.4,ki=16。由上面计算所得参数,结合负荷虚拟同步电机的小信号模型,绘出负荷虚拟同步电机开环传递函数的Bode图如图8所示,可知系统的截止频率ωc为32 Hz/s,自然振荡频率ωn为93 Hz/s,相角稳定裕度为58°,满足要求。因此,文中所提小信号模型及用于设计控制参数的方法是正确的、有效的。 图8 负荷虚拟同步电机开环传递函数Bode图Fig.8 Open-loop transfer function Bode diagram of VSM IGBT的开关频率选为10 kHz。下面分4种工况进行仿真。 工况1:初始稳定运行后,0.3 s时,网侧电压受到扰动出现电压跌落,跌落了5% ;0.5 s时,网侧电压回到正常状态;0.7 s时,网侧电压受到扰动出现电压上升,上升了5% ;0.9 s时,网侧电压回到正常状态。 工况2:初始稳定运行后,0.3 s时,网侧电压受到扰动,频率上升了0.5 Hz ;0.5 s时,网侧电压频率回到正常运行状态。 工况3:初始稳定运行后,0.3 s时,负荷侧突然有内阻为30 Ω的阻性负载加在负荷虚拟电机负荷侧;0.5 s时,负荷侧又有内阻为20 Ω的阻性负载加在负荷虚拟电机负荷侧;0.7 s时,内阻为30 Ω的阻性负载断开。 工况4:初始稳定运行后,0.3 s时,网侧电压发生单相故障,A相电压下降了5%;0.5 s时,A相电压回到正常状态;0.7 s时,A相电压上升5%;0.9 s时,A相电压回到正常状态。 图9为工况1的仿真波形。图9(a)为负荷虚拟同步电机直流侧电压波形。开机后,负荷直流侧电压稳定在600 V。在网侧电压出现波动后,直流侧电压最终总能稳定在600 V。图9(b)为负荷虚拟同步电机无功功率与其他传统控制的无功功率的波形。可见,当电网电压下降时,负荷虚拟同步电机的无功降低,当电网电压上升时,负荷虚拟同步电机的无功增大,支撑电网的电压稳定。 图9 工况1的仿真波形Fig.9 Simulation waveform of case 1 图10为工况2时负荷虚拟同步电机的仿真波形。图10(a)为负荷虚拟同步电机直流侧电压波形。频率的变化意味着大扰动的发生,同时,频率的变化会对电压产生较大影响。由图10(a)可知,系统的频率发生变化时,负荷虚拟同步电机的直流侧电压依旧可以稳定在设定值。图10(b)为负荷虚拟同步电机频率波形。由图10(b)可知,负荷虚拟同步电机无需锁相环,即可准确跟踪网侧电压频率。 图10 工况2的仿真波形Fig.10 Simulation waveform of case 2 图11为工况3的仿真波形。图11(a)为负荷虚拟同步电机有功功率波形,可知突加的并联负载使负荷虚拟同步电机有功功率增大,这与理论相符。图11(b)为负荷虚拟同步电机无功功率波形,直流侧负载变化时,负荷虚拟同步电机无功功率也跟着变化,对电网电压稳定有一定的支撑作用。图11(c)为负荷虚拟同步电机频率波形,由于突加的负载阻值与原负载阻值接近,扰动较大。从图11(c)中可知,大扰动负载的加入或切除,负荷虚拟同步电机的有功功率急剧变化,但频率经过很小的波动过程,总能回到电网工频,支撑了电网的稳定。 图11 工况3的仿真波形Fig.11 Simulation waveform of case 3 图12给出了工况4的仿真波形。 图12 工况4的仿真波形Fig.12 Simulation waveform of case 4 图12(a)为负荷虚拟同步电机直流侧电压波形。开机后,负荷直流侧电压稳定在600 V。在网侧出现单相电压波动后,直流侧电压总能稳定在600 V。图12(b)为负荷虚拟同步电机无功功率与其他传统控制的无功功率的波形。与工况1类似,负荷虚拟同步电机可支撑电网的电压稳定。 文中基于虚拟同步电机技术,提出一种负荷换流器控制小信号模型及控制参数设计方法,用以模拟同步电机的特性。通过Matlab/Simulink搭建模型并进行仿真,仿真结果表明了该方法的正确性和有效性。因此,可以得到以下结论: (1) 所提方法建立了负荷虚拟同步电机的小信号模型,分析了控制参数对系统稳定性的影响程度,可根据实际要求自行设计参数大小。 (2) 所提方法不需要引入锁相环即可准确跟踪电网的电压频率。 (3) 所提方法实现了负荷侧支撑电网稳定的功能,对设计负荷侧控制器来支撑电网稳定提供了一定思路。 [1] 周孝信,鲁宗相,刘应梅,等. 中国未来电网的发展模式和关键技术[J]. 中国电机工程学报,2014,34(29):4999-5008. ZHOU Xiaoxin,LU Zongxiang,LIU Yingmei,et al. Development models and key technologies of future grid in China[J]. Proceedings of the CSEE,2014,34(29):4999-5008. [2] 吕志鹏. 虚拟同步机技术构建“源-网-荷”友好互动新模式 [J]. 供用电,2017,34(2):32-34. LYU Zhipeng. New pattern of source-grid-load friendly interaction based on virtual synchronous machine technology [J]. Distribution & Utilization,2017,34(2):32-34. [3] ZHONG Q C,WEISS G. Synchronverters:Inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics,2011,58(4):1259-1267. [4] ZHONG Q C,NGUYEN P L,MA Z Y,et al. Self-synchronized synchronverters :Inverters without a dedicated synchronization unit[J]. IEEE Transactions on Power Electronics,2014,29(2):617-630. [5] 吕志鹏,盛万兴,钟庆昌,等. 虚拟同步发电机及其在微电网中的应用[J]. 中国电机工程学报,2014,34(16):2591-2603. LYU Zhipeng,SHENG Wanxing,ZHONG Qingchang,et al. Virtual synchronous generator and its applications in micro-grid. Proceedings of the CSEE,2014,34(16):2591-2603. [6] 李 旭,丁 勇,李 勇,等. 虚拟同步发电机的相角控制方法[J]. 电力工程技术,2017,36(1):43-46. LI Xu,DING Yong,LI Yong,et al. Phase angle control method of virtual synchronous generator[J]. Electric Power Engineering Technology,2017,36(1):43-46. [7] 吕志鹏,梁 英,曾 正,等. 应用虚拟同步电机技术的电动汽车快充控制方法[J]. 中国电机工程学报,2014,34(25):4287-4294. LYU Zhipeng,LIANG Ying,ZENG Zheng,et al. Virtual synchronous motor based control scheme of fast charger for electric vehicle application[J]. Proceedings of the CSEE, 2014,34(25):4287-4294. [8] 盛万兴,刘海涛,曾 正,等. 一种基于虚拟电机控制的能量路由器[J]. 中国电机工程学报,2015,35(14):3541-3550. SHENG Wanxing,LIU Haitao,ZENG Zheng,et al. An energy hub based on virtual-machine control[J]. Proceedings of the CSEE,2015,35(14):3541-3550. [9] 范 红,董伟杰,白晓民,等. 基于虚拟同步电动机技术的变频器控制策略研究[J]. 中国电机工程学报,2017,37(15):4446-4453. FAN Hong,DONG Weijie,BAI Xiaojie,et al. A novel frequency-converter control strategy based on virtual synchronous motors [J]. Proceedings of the CSEE,2017,37(15):4446-4453. [10] 鲍陈磊,阮新波,王学华,等. 基于PI调节器和电容电流反馈有源阻尼的LCL型并网逆变器闭环参数设计[J]. 中国电机工程学报,2012,32(25):133-142. BAO Chenlei,RUAN Xinbo,WANG Xuehua,et al. Design of grid-connected inverters with LCL filter based on PI regulator and capacitor current feedback active damping[J]. Proceedings of the CSEE,2012,32(25):133-142. [11] 杨达亮,卢子广,杭乃善,等. 三相电压型PWM整流器准定频直接功率控制[J]. 中国电机工程学报,2011,31(27):66-73. YANG Daliang,LU Ziguang,HANG Naishan,et al. Novel quasi direct power control for three-phase voltage-source PWM rectifiers with a fixed switching frequency[J]. Proceedings of the CSEE,2011,31(27):66-73. [12] 李子欣,李耀华,王 平,等. PWM整流器在静止坐标系下的准直接功率控制[J]. 中国电机工程学报,2010,30(9):47-54. LI Zixin,LI Yaohua,WANG Ping,et al. Novel quasi direct power control method for PWM rectifier in stationary frame[J]. Proceedings of the CSEE,2010,30(9):47-54. [13] 韩华春,丁 昊,黄 地,等. 面向主动配电网的电动汽车充放电功率控制技术[J]. 电力工程技术,2017,36(4):8-13. HAN Huachun,DING Hao,HUANG Di,et al. Electric vehicle power control strategy for active distribution network electric power engineering technology[J]. Electric Power Engineering Technology,2017,36(4):8-13. [14] 倪以信. 动态电力系统的理论和分析[M]. 北京:清华大学出版社,2002. NI Yixin. Theory and analysis of dynamic power system[M]. Beijing:Tsinghua University Press,2002. [15] 胡寿松. 自动控制原理5版[M]. 北京:科学出版社,2007. HU Shousong. Automation control 5thed[M]. Beijing:Science Press,2007. [16] 高丙团,夏超鹏,张 磊,等. 基于虚拟同步电机技术的VSC-HVDC整流侧建模及参数设计[J]. 中国电机工程学报,2017,37(2):534-543. GAO Bingtuan,XIA Chaopeng,ZHANG Lei,et al. Modeling and parameters design for rectifier side of VSC-HVDC based on virtual synchronous machine technology [J]. Proceedings of the CSEE,2017,37(2):534-543. [17] 吴 恒,阮新波,杨东升,等. 虚拟同步发电机功率环的建模与参数设计[J]. 中国电机工程学报,2015,35(24):6508-6518. WU Heng,RUAN Xinbo,YANG Dongsheng,et al. Modeling of the power loop and parameter design of virtual synchronous generators[J]. Proceedings of the CSEE,2015,35(24):6508-6518.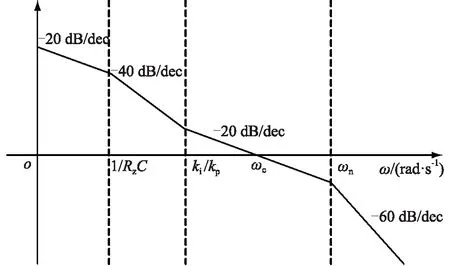
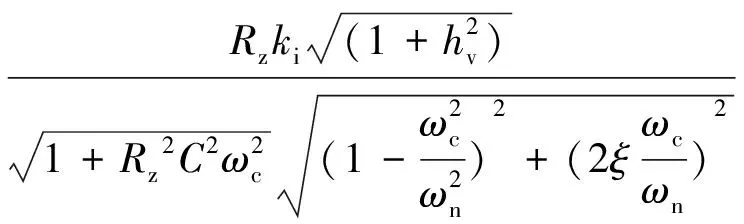
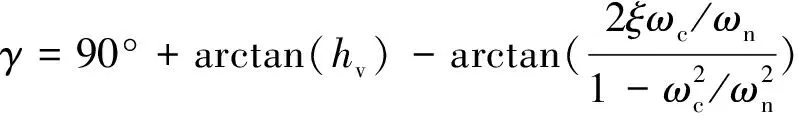
5 仿真
5.1 仿真算例

5.2 仿真结果
6 结论

