基于两层规划的电力系统N-K故障分析方法
刘国静, 李 娟, 谈 健, 李 琥, 史 静, 胡晓燕
(1. 国网江苏省电力有限公司经济技术研究院, 江苏 南京 210008;2. 国网江苏省电力有限公司电力科学研究院,江苏 南京 211103)
0 引言
电力系统N-K故障分析是电力系统规划和运行中的常用手段,用以校验当系统中K个元件停运后系统运行状态是否在允许的安全范围内[1]。K的取值一般为1或2,即常见的N-1或N-2校验。近年来发生的国内外大停电事故表明,加强对电网中严重N-K故障(K≥2)的分析、识别和预防连锁故障对于保证大电网安全可靠运行具有十分重要的意义[2-7]。
目前电力系统N-K故障分析一般是采用组合遍历的方式,然而随着系统元件数量和分析故障重数的增加,故障组合的数量将呈指数级增长,日渐难以满足大电网分析计算的需要。为提高电力系统N-K故障分析的计算效率,近年来学者们开展了大量研究。文献[8]在计算中采用了因子表附加链技术和动态网络接线分析方法,能够较好地保证计算精度和速度。文献[9]利用导纳矩阵的稀疏性,并结合矩阵部分重新因子化法和快速前代等技术,有效减少了不必要的计算,节省了计算时间。为快速确定故障后发电机组输出功率再调整量和切负荷量,文献[10]提出了一种基于交流灵敏度的反向等量配对调整法,具有计算效率高、实用性强的优点。此外,并行计算技术在该领域也得到了应用。文献[11]通过直流潮流进行开断故障的快速扫描,并将多个时段的计算任务分配到不同的计算进程,对于单时段内的分析计算采用多线程并行计算的方式,有效提高了整体计算速度。文献[12]充分利用N-K故障分析问题的时空弱耦合特征,对于大规模电网采用分区并行计算,对于多时段的静态安全校核采用分时段并行计算,具有较高的计算效率。
上述研究在提高电力系统N-K故障分析的计算效率方面取得了一定的成效,但是仍没有摆脱组合遍历的框架。文中尝试从另一个角度,将求取N-K故障分析中最严重故障的问题描述成两层规划模型,借助最优化原理,通过寻优方式确定故障组合,以期减少传统组合遍历方式的计算量。
为减轻通过组合遍历方式进行电力系统N-K故障分析带来的计算负担,文中将该问题描述成两层规划模型,通过优化求解的方式寻求造成电网失负荷量最大的故障组合,对此电力系统N-K故障分析的问题提供了一个新的研究思路。
1 计算流程
传统的电力系统N-K故障分析需要对预想事故集中可能出现的事故进行组合遍历。对于每一种故障组合,在分析中首先假设组合中的元件处于强迫停运状态,在此基础上进行电网拓扑分析和潮流计算。若出现线路潮流约束或母线电压越限,还需要通过调整发电机组输出功率、发电厂母线电压等手段进行安全校正操作[13-15]。安全校正过程一般是以切负荷量最小、调整时间最短等为目标(图1以切负荷量为例进行说明)。若最终在某些故障组合下出现切负荷的情况,则说明当前电网运行方式无法满足N-K校验的要求,一般需要对发电方式或网架结构进行适当的调整。传统的电力系统N-K故障分析流程如图1所示。在电力系统N-K故障分析中,造成损失最严重的故障组合对于安全分析而言具有尤为重要的意义,可以更为直接地反映电网安全水平。基于最优化原理,分析流程如图2所示。
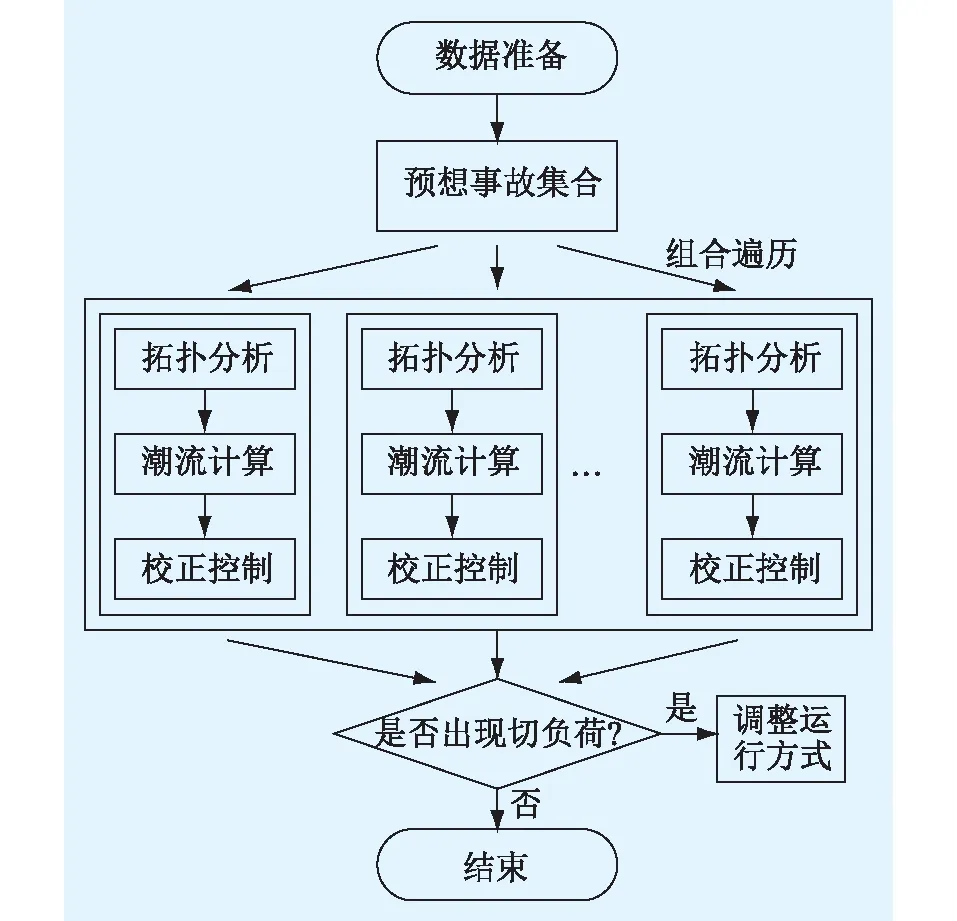
图1 传统的电力系统N-K故障分析流程Fig. 1 The flowchart of traditional power system N-K analysis
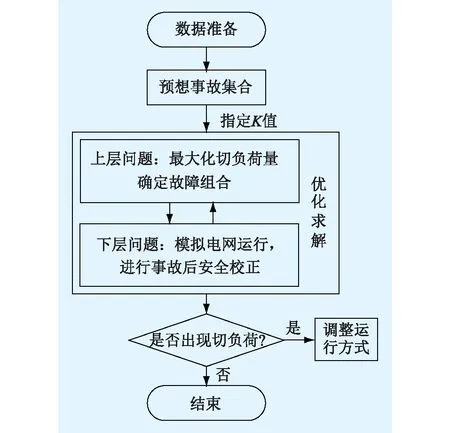
图2 文中分析流程Fig. 2 The flowchart of the analysis method in this paper
上述分析流程的特点在于通过两层规划模型的优化求解代替传统的组合遍历。模型将电网切负荷量作为故障引起电网损失的评价指标,上层问题在故障重数K给定的条件下,寻求能够引起电网切负荷量最大的故障组合,而下层问题则针对上层问题决策的故障组合,模拟电网事故后的运行情况,在满足电网各类运行约束的条件下,通过调整发电机组的输出功率最小化电网切负荷量。最终,上层问题的目标函数值将等于各故障组合所引起的电网最小切负荷量中的最大值。通过对模型的求解,能够直接给出引起电网切负荷最大的故障组合。
2 数学模型
2.1 上层问题
文中模型暂不考虑无功电压的影响,建立直流潮流条件下的数学模型。上层问题目标函数可表示为:
(1)
(2)
式中:L为线路集合;K为所分析的故障重数。
2.2 下层问题
下层问题通过发电机组输出功率的再调整,最小化电网切负荷量,目标函数可表示为:
(3)
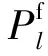
(1) 线路传输容量约束,即:
(4)
(5)
(6)

当线路l正常运行时,vl=1,由式(4)、式(5)可知,线路l上的有功功率应满足:
(7)
由式(6)可知,此时vl=1,有:
(8)

(2) 节点功率平衡约束。对于节点n,应满足注入功率与流出功率相等,即:
(9)
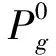
(3) 发电机组最大调整量约束。发电机组g在故障后的再调整量ΔPg应满足如下约束:
-rgΔt≤ΔPg≤rgΔt
(10)
式中:rg为发电机组g最大调节速率;Δt为允许的调整时间,一般为5~10 min。
(4) 机组输出功率范围约束,即:
(11)

3 求解流程
文中模型属于两层规划模型,其中下层问题为混合整数线性规划模型。两层优化模型常用的求解方法包括极点搜索法、分支定界法、互补旋转法、下降方向法、罚函数法、智能搜索方法等[16],采用智能搜索算法中常用的遗传算法[17-18]进行求解,求解流程如图3所示。
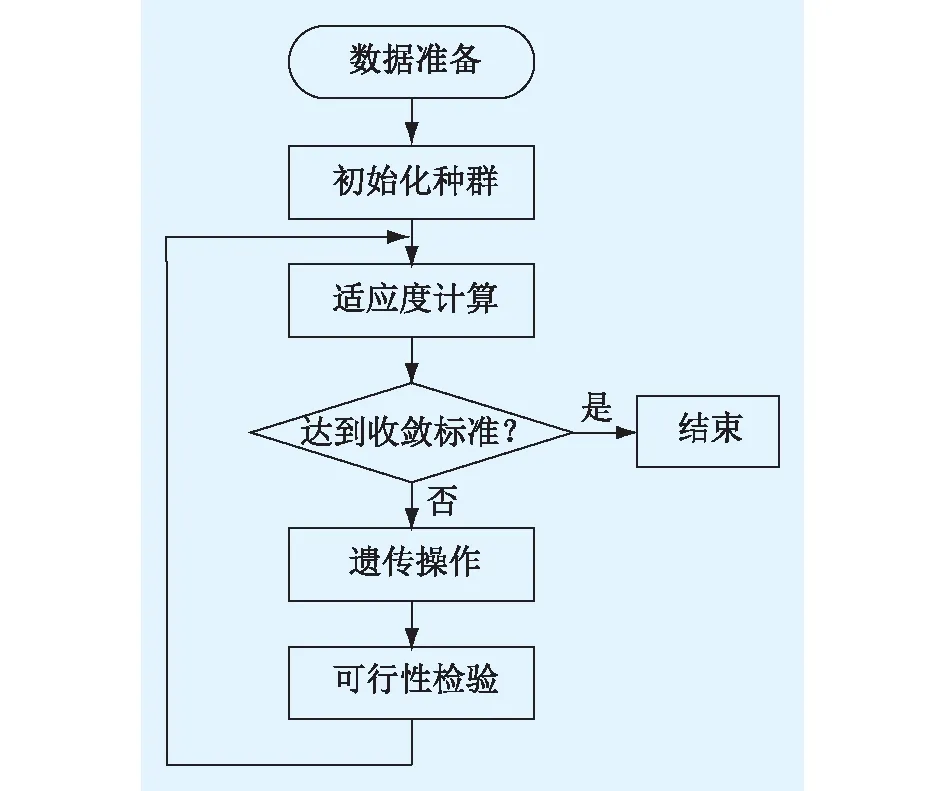
图3 遗传算法求解流程Fig. 3 The flowchart of GA solving process
(1) 初始化种群。采用二进制编码方式,种群中每一个体均由N位组成(N为线路数量)。在初始化阶段,从N位中随机选择K位设置编码为0(K为所研究的故障重数),表示对应线路故障停运,其他设置为1。
(2) 适应度计算。将下层问题目标函数值,即引起的电网最小切负荷量作为个体适应度。对于种群中的个体,可求解通过下层问题的获得适应度,下层问题采用CPLEX软件包求解[16]。
(3) 收敛判据。根据最大迭代次数作为迭代过程的收敛判据。
(4) 遗传操作。遗传操作包括选择、交叉和变异运算。其中,根据个体适应度,采用轮盘赌的方式确定个体被选择到下一代的概率,随机选择遗传到下一代的个体。个体间的交叉运算采用单点交叉方式。
(5) 可行性检查。经过遗传、交叉和变异运算,个体所对应的故障停运线路条数可能不等于K,无法满足上层问题约束条件。对于不满足的个体,可行性检查通过随机选择的方式改变部分编码,将编码对应数值为0的位数重新调整为K。
4 算例分析
4.1 IEEE-14节点算例系统
首先以IEEE-14节点系统为例进行说明。IEEE-14节点系统网络参数取自文献[19],发电机组数据如表1所示,负荷数据如表2所示。设置种群数量为100,交叉概率为1.0,变异概率为0.001。
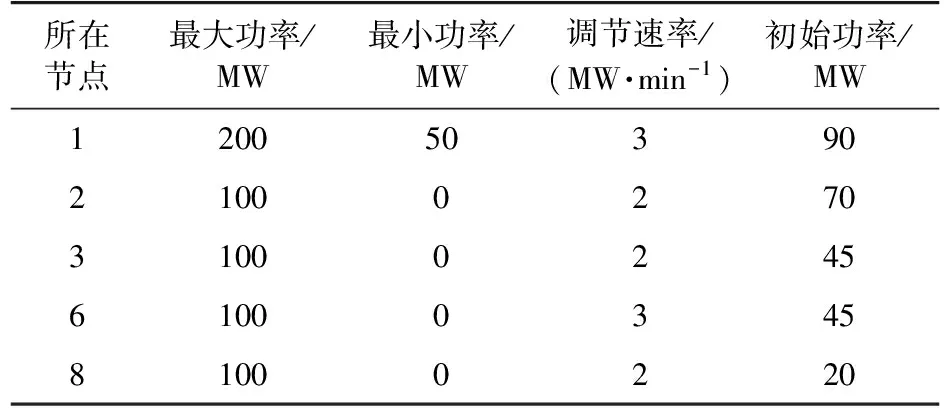
表1 机组数据Tab.1 Generator data

表2 负荷数据Tab.2 Load data
为说明文中模型的有效性,将模型计算结果与传统组合遍历方式计算结果进行对比。在K取不同值时,计算结果如表3所示。
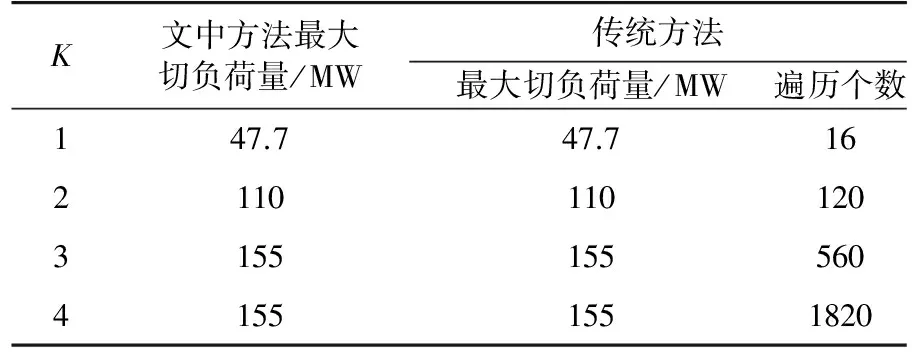
表3 结果比较Tab.3 Results comparison between two methods
可见,方法计算结果与传统组合遍历方式的计算结果一致,验证了通过求解两层优化模型进行寻优的有效性。
4.2 IEEE-118节点算例系统
为说明文中方法在大系统电网安全分析中的优势,进一步以IEEE-118节点算例系统为例进行说明。该系统包含186条线路,54台机组,91个负荷节点。若不计预想事故集的预筛选,K=3时,组合遍历的故障数量将超过100万个,K=4时,组合遍历的故障数量将接近5000万。传统的方法显然难以直接适用,需要采取预想事故集缩减、故障排序等启发式简化措施。文中方法通过智能搜索,能有效减少计算时间。
以K=3为例,计算机配置为AMD A8-6410处理器,主频2.0 GHz,内存4 G,传统方法耗时约8.04 h,文中方法约6.21 h,具有较为明显的计算速度优势。
5 结语
为减轻通过组合遍历方式进行电力系统N-K故障分析带来的计算负担,将该问题描述成两层规划模型,通过优化求解的方式寻求造成电网失负荷量最大的故障组合,为电力系统N-K故障分析问题提供了一个新的研究思路。
文中模型基于直流潮流,主要关注造成电网失负荷量最大的故障组合,在后续研究中有必要进一步考虑线路潮流越限量、母线电压越限量等指标,同时需要进一步研究如何给出寻优过程的次优解,以便分析所有可能对系统的安全稳定运行造成威胁的故障组合。
[1] 王锡凡. 现代电力系统分析[M]. 北京:科学出版社, 2009.
WANG Xifan.Morden power system analysis[M]. Beijing: Science Press,2009.
[2] 高 翔, 庄侃沁, 孙 勇. 西欧电网“11.4”大停电事故的启示[J]. 电网技术, 2007, 31(1):25-31.
GAO Xiang,ZHUANG Kanqin,SUN Yong. Lessons and enlightenment from blackout occurred in UCTE grid on November 4 [J]. Power System Technology,2007,31(1):25-31.
[3] CHEN Q, MCCALLEY J D. Identifying high risk N-K contingencies for online security assessment[J]. IEEE Transactions on Power Systems,2005, 20(2):823-834.
[4] KIRSCHEN D S, JAYAWEERA D, NEDIC D P, et al. A probabilistic indicator of system stress[J]. Power Systems IEEE Transactions on, 2004, 19(3):1650-1657.
[5] 易 强,万书鹏,彭 辉,等. 调度与变电站一体化系统远程维护安全防护设计[J].江苏电机工程,2015,34(1),40-42,46.
YI Qiang,WAN Shupeng,PENG Hui,et al.Design of security protection for remote maintenance in dispatch and substation integrated system[J].Jiangsu Electrical Engineering,2015,34(1),40-42,46.
[6] 张 煦,张向伍. 计及设备故障检修的电网可靠性与经济性分析[J]. 江苏电机工程,2016,35(2),60-64.
ZHANG Xu,ZHANG Xiangwu. Analysis for the reliability and economic of power system considering maintenance[J]. Jiangsu Electrical Engineering, 2016,35(2),60-64.
[7] 丁 平, 李亚楼, 徐得超,等. 电力系统快速静态安全分析的改进算法[J]. 中国电机工程学报, 2010, 30(31):77-82.
DING Ping, LI Yanlou, XU Dechao, et al. Improved algorithm of fast static state security analysis of power system[J].Proceeding of the CSEE, 2010, 30(31):77-82.
[8] 何 洋, 洪 潮, 陈昆薇. 稀疏向量技术在静态安全分析中的应用[J]. 中国电机工程学报, 2003, 23(1):41-44.
HE Yang, HONG Chao, CHEN Kunwei. Study of sparse vector techniques applied to contingency analysis[J]. Proceeding of the CSEE, 2003, 23(1):41-44.
[9] 李海涛, 孙 闻, 赵 兵,等. 基于交流灵敏度的在线安全控制策略[J]. 电力系统及其自动化学报, 2012, 24(1):32-36.
LI Haitao, SUN Wen, ZHAO Bing, et al. Online security control analysis based on sensitivity method[J]. Proceeding of the CSU-EPSA, 2012, 24(1):32-36.
[10] 李 峰, 李虎成, 於益军,等. 基于并行计算和数据复用的快速静态安全校核技术[J]. 电力系统自动化, 2013, 37(14):75-80.
LI Feng, LI Hucheng, YU Yijun, et al. Fast computing technologies for static security checking based on parallel computation and data reuse[J]. Automation of Electric Power System, 2013, 37(14):75-80.
[11] 王兴志, 严 正, 沈 沉,等. 基于面向服务架构的调度计划安全校核网格计算[J]. 电力系统保护与控制, 2011, 39(24):90-95.
WANG Xingzhi, YAN Zheng, SHEN Chen, et al. Grid computing of operation scheduling with security constraint based on SOA[J]. Power System Protection and Control, 2011, 39(24):90-95.
[12] 傅 旭. 电力系统静态安全混合控制方法[J]. 电力自动化设备, 2017(1):124-130.
FU Xu. Hybrid control of power system static security[J]. Electric Power Automation Equipment, 2017(1):124-130.
[13] 傅 旭, 王锡凡, 张 钦,等. 电力系统静态安全分析中的校正控制算法[J]. 中国电力, 2007, 40(11):33-37.
FU Xu, WANG Xifan, ZHANG Qin, et al.New approach of corrective for static security analysis in power systems[J]. Electric Power, 2007, 40(11):33-37.
[14] 王孟夏, 韩学山. 基于电热协调的电网安全校正控制方法[J]. 电力系统自动化, 2011, 35(12):32-36.
WANG Mengxia, HAN Xueshan. Realization of security corrective control considering electro-thermal coordination[J]. Automation of Electric Power Systems, 2011, 35(12):32-36.
[15] 王广民,万仲平,王先甲. 二(双)层规划综述[J]. 数学进展,2007, 36(5):513-529.
WANG Guangmin, WANG Zhongping, WANG Xianjia. Bibbiography on bilevel programming[J]. Advances in Mathematics, 2007, 36(5):513-529.
[16] 聂明林, 汪 沨, 陈 春,等. 考虑可靠性的配电网网架多目标规划[J]. 电力系统及其自动化学报, 2016, 28(1):10-16.
NIE Minglin, WANG Feng, CHEN Chun, et al. Multi-objective distribution network planning considering reliability[J]. Proceeding of the CSU-EPSA, 2016, 28(1):10-16.
[17] 刘东奇, 王耀南, 袁小芳. 电动汽车充放电与风力/火力发电系统的协同优化运行[J]. 电工技术学报, 2017, 32(3):18-26.
LIU Dongqi, WANG Yaonan, YUAN Xiaofang. Cooperative dispatch of large scale electric vehicles with wind-thermal power considering generating system[J].Transactions of China Electrotechnical Society, 2017, 32(3):18-26.
[18] 王一哲, 汤 涌, 董朝阳. 电力市场环境下输电网混合性规划模型[J]. 电力系统自动化, 2016, 40(13):35-40.
WANG Yizhe, TANG Yong, DONG Zhaoyang. Hybrid criterion planning model for transmission system planning under electricity market environment[J]. Automation of Electric Power Systems, 2016, 40(13):35-40.
[19] 张伯明, 陈寿孙. 高等电力网络分析[M]. 北京:清华大学出版社, 1996.
ZHANG Boming, CHEN Shunsun. Adavanced power network analysis[M].Beijing: Tsinghua University Press, 1996.

