基于随机优化的综合能源系统能量管理
季振亚 黄学良 张梓麒 孙厚涛 赵家庆 李 军
(1东南大学电气工程学院, 南京 210096)(2江苏省智能电网技术与装备重点实验室, 南京 210096)(3国网苏州供电公司, 苏州 215004) (4南京工程学院电力工程学院, 南京 211167)
综合能源系统(integrated energy system,IES)可以打破多能流子系统相对割裂的状态,实现能源高效和梯级利用,具有调整能源结构、促进节能减排等社会效益,符合我国能源互联网发展需求[1-2].IES的能量管理充分考虑多能流耦合元件,如热电联产机组(combined heat and power,CHP)、电动热泵(electrical heat pump,EHP)等设备,在满足子系统供需平衡与运行约束的前提下,提高能源综合利用效率、降低用能成本、促进可再生能源消纳,通过提升经济与环境效益来直接提高IES的实用价值[3-4].其中,电动汽车的快速发展使电力系统与交通能源系统的耦合成为趋势.然而,电动汽车充电的随机性使得规模化电动汽车接入可能带来电力系统新的负荷尖峰和过载[5].通过进一步加入有序充电策略,IES能量管理可以适应快速增长的电动汽车充电需求,减少承担高峰负荷的系统建设.
模型预测控制(model predictive control,MPC)始于20世纪70年代的工业控制领域,在当前时刻根据预测模型求解预测时域内的控制指令序列,但仅执行当前时刻的控制指令,下一时刻重复这一过程[6].近年来,基于上述原理的能量管理受到普遍关注[7],如用于用能支出的最小化[8].常见的MPC基于单一确定性模型,即DMPC(determined MPC).随着可再生能源发电系统(renewable energy system,RES)出力、负荷等短期预测能力的增强[9-11],变量随机性逐步获得精确的定量表述,基于随机优化的模型预测控制(stochastic MPC,SMPC)日益受到重视.SMPC适用于连续型概率分布和具有离散特征的随机性模型[12],但由于连续变量将导致SMPC计算时间与空间成本极大增加,因此一般采用含概率的离散场景表达随机性[13-14].文献[15]验证了考虑随机优化的微网能量管理经济性,但随机场景较少、电动汽车数量恒定、未考虑时域滚动;文献[16]实现了风储系统基于时域滚动的随机优化,未涉及电动汽车,且预测场景数量有限;文献[17]考虑风机出力多场景下的电动汽车有序充电,但未考虑滚动时域和计算速度,且电动汽车数量不变.总体来说,目前绝大多数考虑随机性与滚动求解的能量管理以RES为主,即使考虑了电动汽车接入,也往往忽略电动汽车在IES中流动的特征.
实际应用中,在MPC预测时域内,已接入IES的电动汽车会随着车主驶离导致该车辆离线,新抵达的电动汽车也有可能接入空闲的充电桩,该特征与其他固定型设备特征产生了区别.而当前普遍的电动汽车有序充电策略仅针对单一车辆本身,对IES中接入电动汽车的变化考虑不足.此外,目前IES能量管理多数仅考虑单一的快速求解策略,即在包含随机性与加快求解速度中从简择一处理,但MPC方法包括时域滚动的特征,对实时求解能力要求较高,上述简化将产生优化效果受削弱或计算速度受制约的问题.
本文以IES包含的电动汽车充电桩为有序充电的控制单元,将充电负荷作为可延时负荷,应用SMPC策略,建立IES总用能成本最低的2阶段随机规划模型,通过求解期望获得决策变量,其中,考虑了多种输入变量的随机性.为实现在线滚动求解,一方面采用场景生成与削减技术实现对输入变量预测场景集的合理利用,另一方面结合Benders分解算法进一步提高计算速度.所提方法在一个区域IES中仿真验证,结果表明该方法在保证求解速度的基础上,具有良好的经济性.
1 区域多能流综合能源系统建模
1.1 系统结构模型
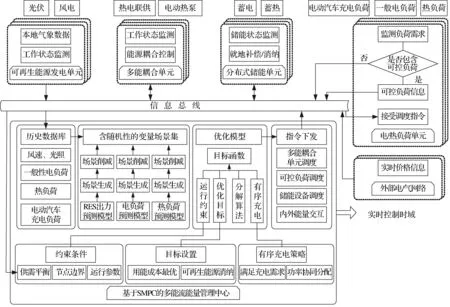
IES由分布于同区域的电力子系统、天然气子系统、热力子系统、交通子系统等组成,结构如图1所示.耦合元件实现子系统间的耦合与作用,消耗系统中一种或多种能源产生其他能源,包括CHP、EHP、燃气锅炉、RES等.非耦合元件一般针对单一能源的生产、使用和存储,包括负荷、储电单元、储热单元等.在能量管理系统的综合优化调度下,IES作为整体获得协同效益.

图1 多能流区域综合能源系统结构示意图
1.2 多能流耦合约束
IES能量管理的先决条件是保持供需平衡.定义多输入-多输出转换模型,输入端含耦合元件矩阵Wc={W1,W2,…,Wx}T与非耦合元件矩阵Mnc={M1,M2,…,My}T,其中,x,y分别为耦合元件与非耦合元件数;输出端为负荷矩阵Ld={L1,L2,…,Ln}T,n为负荷种类;耦合元件在各能流间作用关系通过耦合矩阵C建立,矩阵元素∂Ln/∂Wx≠0表示负荷n与耦合元件x之间存在转换关系,否则无关.约束关系为
Ld=CWc+Mnc
(1)
图1中,输出端包括用电功率Pe,t与热功率Ph,t,电动汽车充电负荷功率Pev,t包含于Pe,t内,即Pe,t=Preg,t+Pev,t,Preg,t为一般用电负荷功率,功率平衡表达式为
(2)
式中,ηce,t,ηch,t分别为t时刻CHP电转换效率和热转换效率;Xc,t为二元变量,Xc,t=1表示t时刻CHP工作,Xc,t=0表示t时刻CHP关停;ηl,ηh分别为燃气锅炉气-热转换效率和EHP电-热转换效率;γr,t为t时刻RES工作参数;Pr为RES额定功率;Pc,t,Pl,t,Ph,t分别为t时刻CHP、燃气锅炉、EHP的输入功率;Pex,t,Pb,t,Pw,t分别为t时刻外电网输入IES电功率(输入为正)、储电单元充放电功率(放电为正)和储热单元蓄放热功率(供热为正).
其他假定条件包括:在同一采样间隔Δt内,各模块功率、工作状态保持不变;设备模块损耗折算在各模型表达式中,不考虑子网络传输损耗.
1.3 设备运行约束
CHP常用燃气轮机实现,当载荷低于额定功率一定比例时,效率下降.要求燃气轮机工作在如下功率区间:
Pcmin≤Pc,t≤Pcmax
(3)
式中,Pcmin为最小功率;Pcmax为最大功率.
作为常用供热设备,燃气锅炉约束条件为
0≤Pl,t≤Plmax
(4)
式中,Plmax为燃气锅炉的最大输出热量.
EHP是电-热耦合元件,约束条件为
Phmin≤Ph,t≤Phmax
(5)
式中,Phmin,Phmax分别为EHP最小和最大功率.
RES以风机为例,约束条件为
(6)
式中,vt为风机所在环境的当前风速;vin,vout,vr分别为所装风机的切入风速、切出风速与额定风速.
储电单元以电池储能系统为例,约束条件为
(7)
Emin≤Eb,t≤Emax
(8)
Pbdmax≤Pb,t≤Pbcmax
(9)
式中,Eb,t为电池组的当前蓄电量;Eb,t-1为电池组的上一时刻蓄电量;Emin为电池组的最小蓄电量;Emax为电池组的最大蓄电量;ηb为自放电损失效率;ηbc,ηbd分别为充、放电效率;Pbcmax,Pbdmax分别为最大充、放电功率.
储热单元以蓄热水罐为例,约束条件为
(10)
Cmin≤Cs,t≤Cmax
(11)
Pwdmax≤Pw,t≤Pwcmax
(12)
式中,Cs,t为蓄热水罐的当前蓄热量;Cs,t-1为前一时刻蓄热量;Cmin为最小蓄热量;Cmax为最大可蓄热量;ηw为散热效率;ηwc,ηwd分别为蓄热和放热效率;Pwcmax,Pwdmax分别为最大蓄、放热功率.
1.4 电动汽车有序充电过程
IES中电动汽车数量是动态的,但充电桩数量在预测时域内可认为不变,因此本文以充电桩作为控制对象,假设共接入Nz个充电桩,其功率Pz由电动汽车及充电桩共同决定,且充电时间恒定.认为车主均同意参与有序充电,在电动汽车接入第z(z∈[1,Nz])个充电桩时,车主需设置预期离开时刻tz,set和离开时刻目标电量Ez,set,系统判断并提示车主不能高于最大可充入电量.
基于MPC的能量管理需要掌握预测时域内各时刻电动汽车负荷是否可控及其充电需求.将电动汽车有序充电行为判据分为2类过程:① 判断电动汽车充电负荷是否可控.将可适当延时而不影响车主驶离时实现目标电量的电动汽车归为可控负荷,如图2(a)所示.② 预测时域内电动汽车充电负荷序列的形成,使目标函数具有未来时段的电动汽车充电负荷信息,以便于进行能量管理,过程如图2(b)所示.
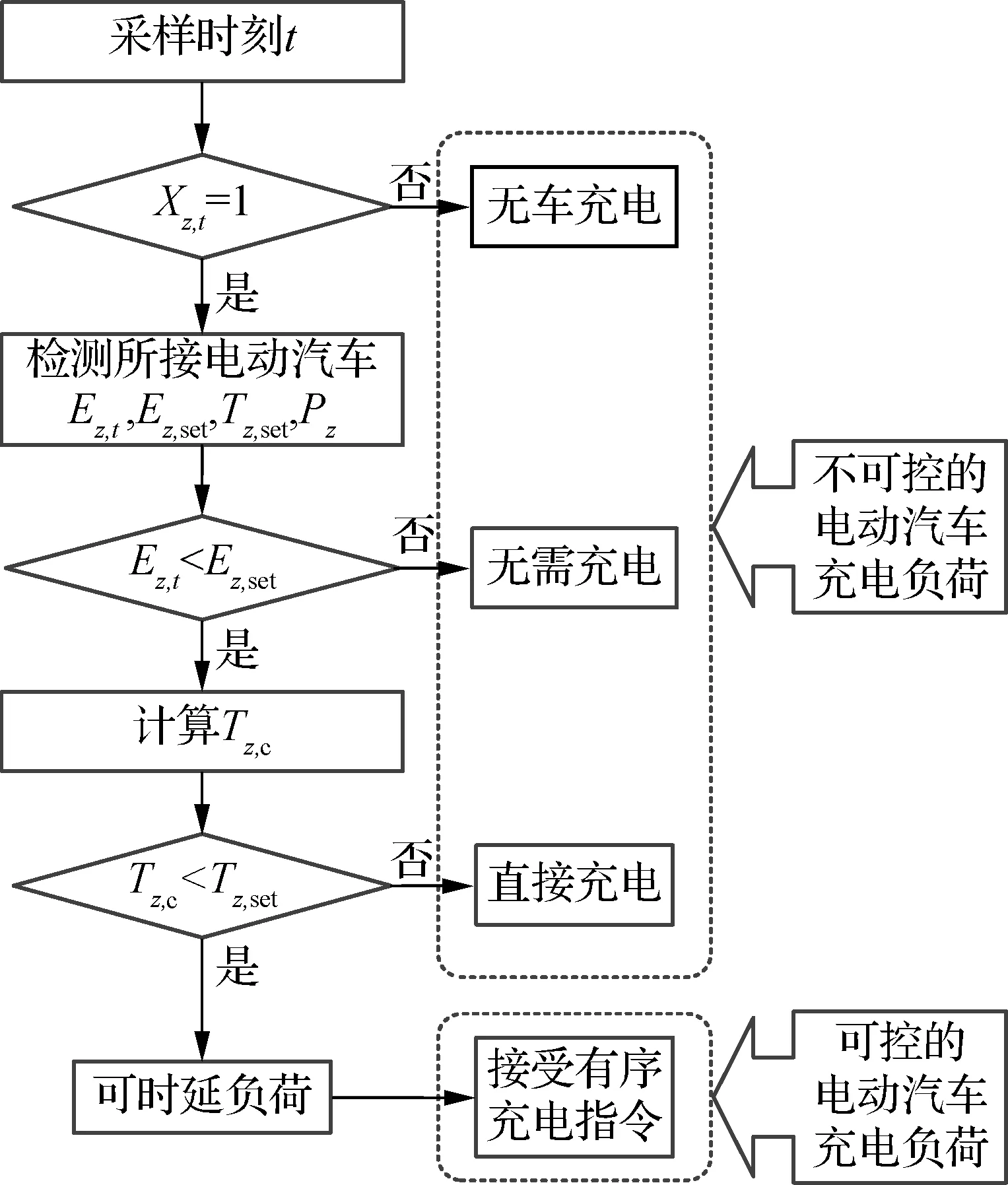
(a) 电动汽车充电负荷可控状态判断流程
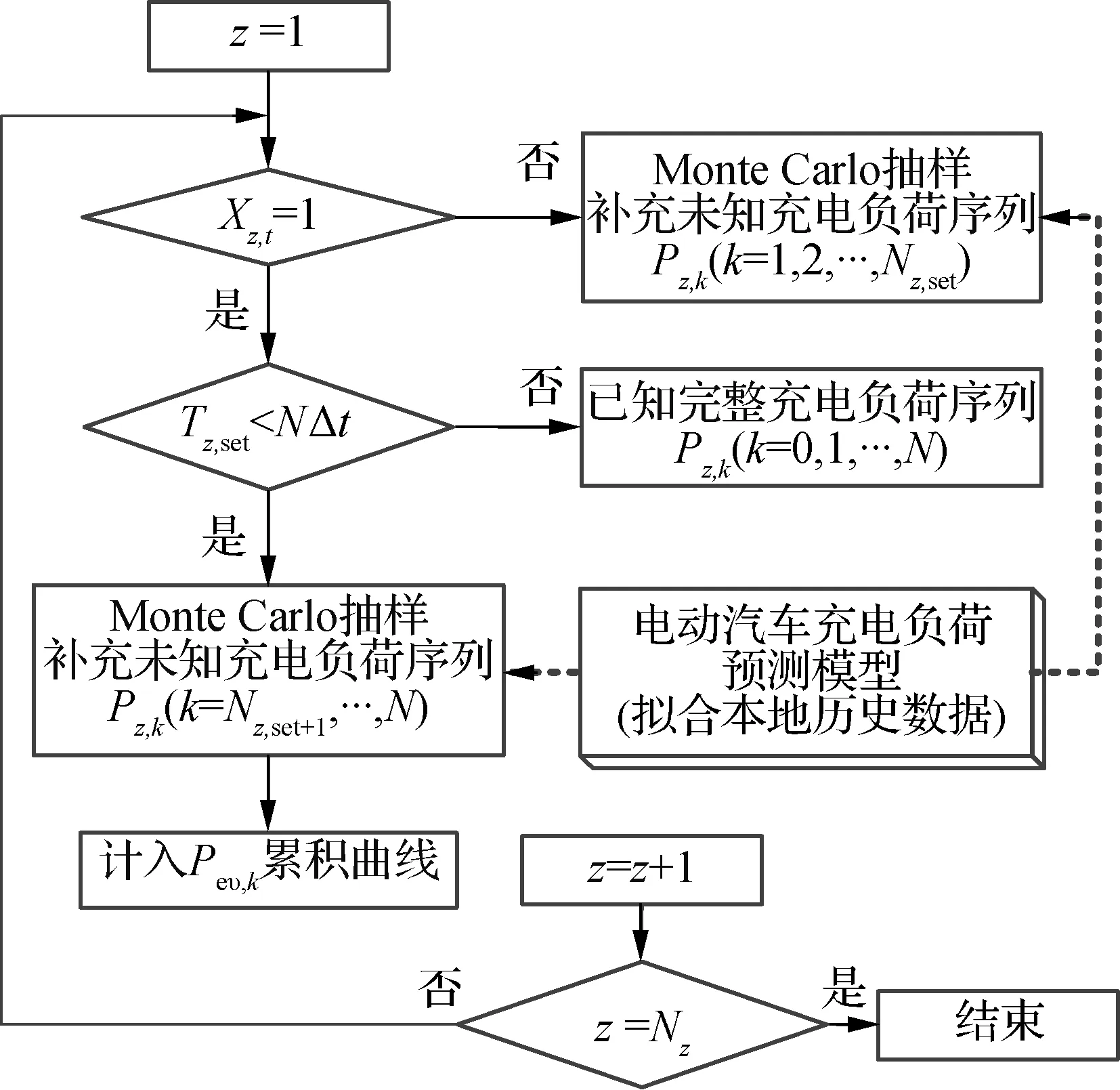
(b) 适用于MPC的电动汽车充电负荷序列形成过程
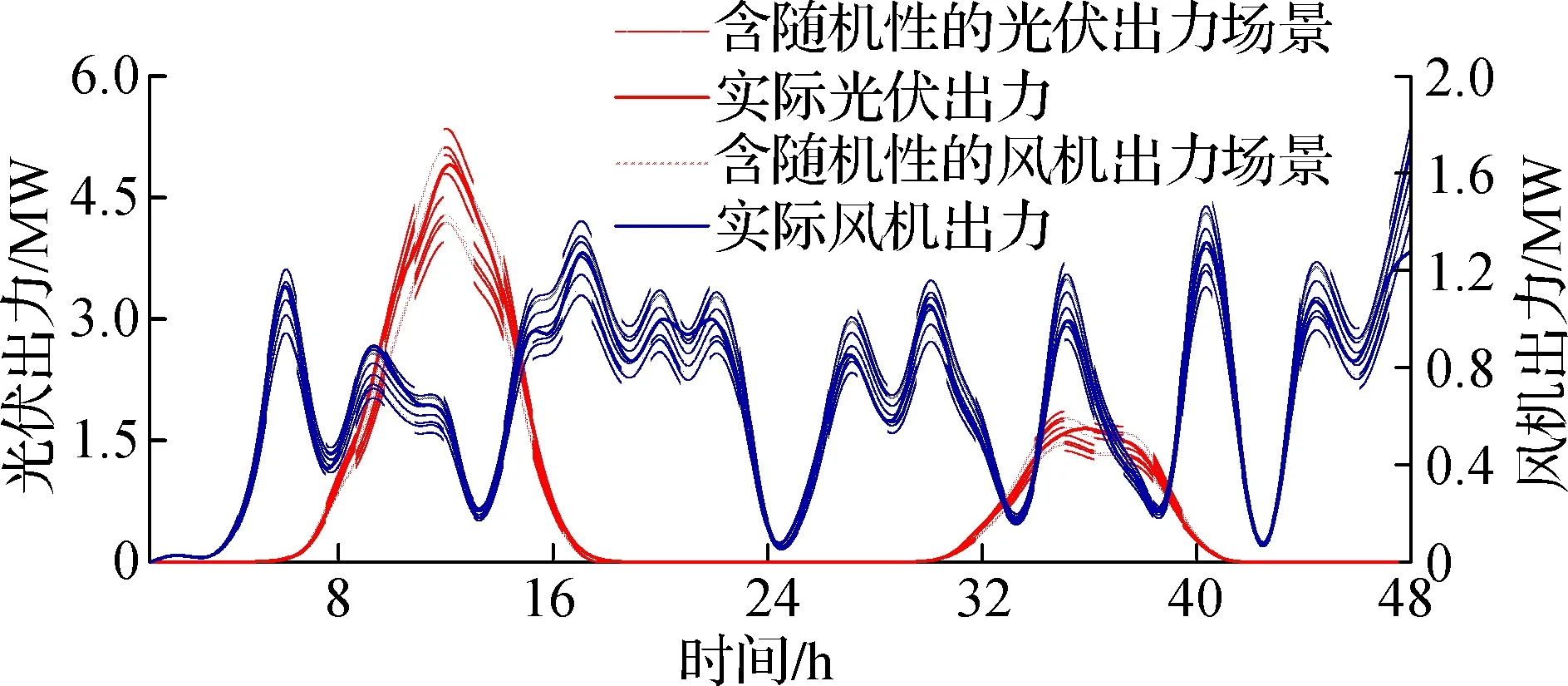
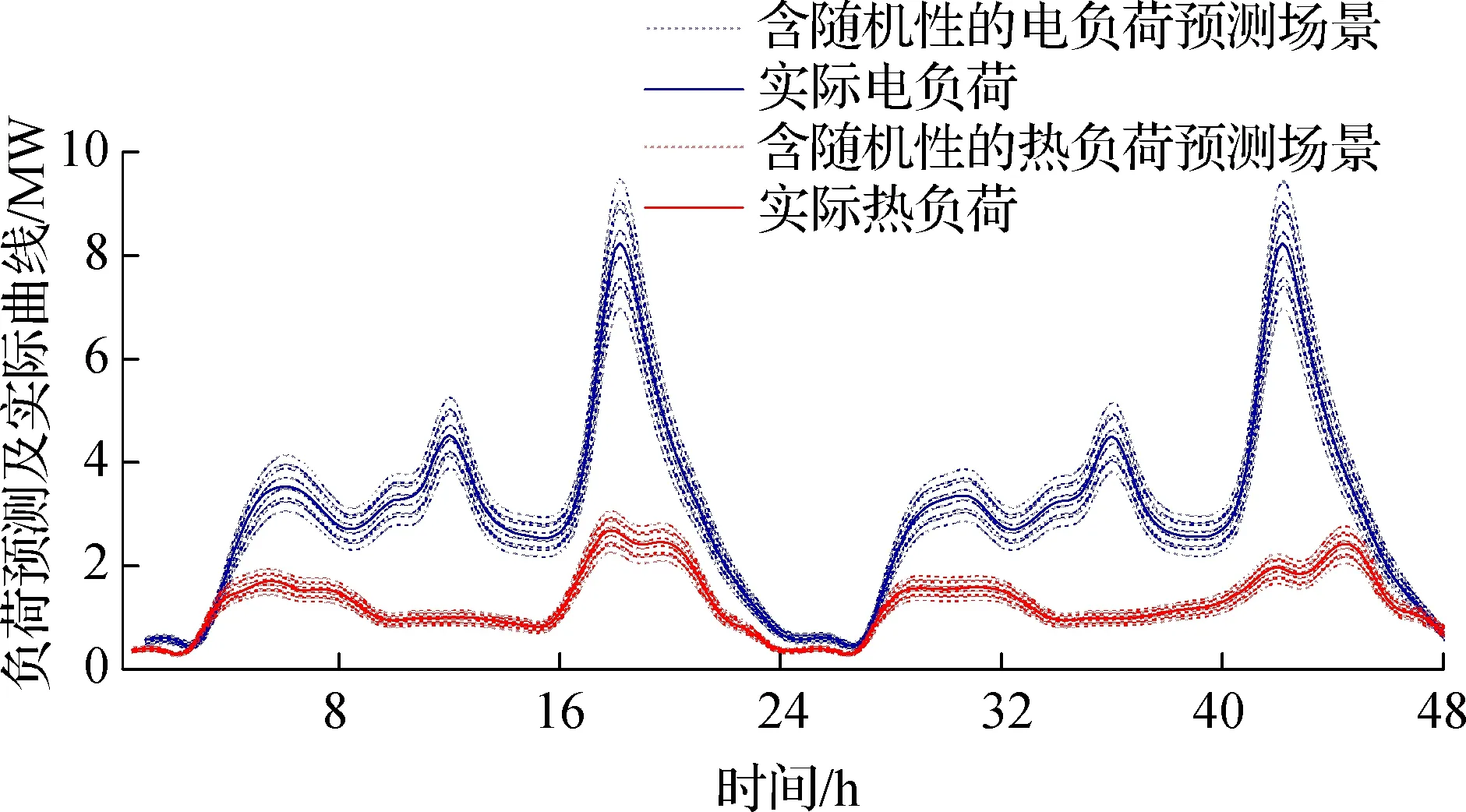
图2(a)以充电桩z为例说明t时刻充电负荷可控状态的判断流程,以判别所接电动汽车是否可以参与有序充电.首先,检测充电桩z是否接有电动汽车,定义二元变量Xz,t,当Xz,t=1时表明该充电桩有车辆接入,检测当前蓄电状态Ez,t并读取Ez,set和tz,set.比较Ez,t与Ez,set,若Ez,t (13) 车主预期离开时刻与当前时刻之间的时长Tz,set=tz,set-t,若Tz,c 图2(b)是目标函数中电动汽车总充电负荷序列形成过程.当充电桩z所接电动汽车离开时刻早于预测时域时,[t,t+NΔt]内存在未知充电负荷信息,Tz,set按Δt向上取整,得Nz,set=[Tz,set/Δt],利用电动汽车充电负荷预测模型,并与IES中电动汽车的历史数据拟合,对[t+(Nz,set+1)Δt,t+NΔt]时段内未知充电需求进行Monte Carlo抽样;当前时刻无电动汽车接入时,[t+Δt,t+NΔt]时段内的未知充电需求用相同方法补足. 预测时域内每个时间节点的累积充电负荷序列Pev,k由可延时充电功率Pz,ctr,k和不可延时充电功率Pz,k(k∈[t,t+NΔt])组成,即 (14) Pz,ctr,k∈{0,Pz,k} (15) (16) 目标函数接到充电负荷序列指今后,对可参与有序充电的充电桩,下发当前充电或延时充电指令;对不参与有序充电的充电桩,按不可控负荷处理. 在多目标随机优化问题的求解中,两阶段随机规划是常见的方法,该方法适用于求解随机模型在期望下的最优解[18].本文针对IES结构,目标函数两阶段分别定义为:第1阶段表示CHP启停及出力成本,第2阶段表示除CHP外其他成本的可控变量.第1阶段发生在包含随机性的输入变量确定之前,CHP启停状态与上一时刻工作状态有关,且一旦发生变化,IES的供能组成会发生明显调整;而第2阶段可控变量的调节相对灵活,可以作为优化目标函数结果的补偿变量,弥补第1阶段带来的可行解或最优解问题.目标函数根据第2阶段随机变量所决定的期望解寻找第1阶段的最优解,使第1阶段成本和第2阶段的成本期望值之和最小.在考虑出力全额消纳的情况下,使预测时域[t,t+NΔt]内总用能成本最小,目标函数表达式为 (17) 式中,F(Xc,k,Xc,k-1)为CHP在k时刻改变前一时刻启停状态的罚函数,表达式如下: F(Xc,k,Xc,k-1)=λsu,k(Xc,k-Xc,k-1)+λsd,k(Xc,k-1-Xc,k) (18) 式(17)受式(1)~(16)的约束.其他假设条件包括:RES无一次能源成本,可切除负荷按实际切除负荷量补贴,可延时负荷无补贴. 考虑随机性与加速求解的总能量管理流程如图3所示.集中控制结构下,将IES中多个随机变量的场景集与采集的其他状态变量作为输入变量,求解后向各控制单元下发当前时刻的控制参数指令.包含随机性的未来状态预测参与当前决策,使总时段内的经济性获得提升;滚动优化的执行方式,使未来状态的不确定性不影响下一时刻系统的能量管理,不会导致供能不平衡等问题. 图3 考虑随机性与加速求解的能量管理流程 场景树技术即为适用于不确定性的样本集合[19].随着IES能量管理中以随机模型表示变量的增加,多个场景树的合并导致总场景数迅速增加,求解效率受到制约. 场景削减方法通过尽可能少的场景数量来提高场景描述效率,同时保证场景抽样足以充分表达随机特征.针对已充分生成的场景集,利用基于最大削减的同步回代场景削减技术[20],减少每个场景集的场景数,在保证覆盖率的同时获得一组与初始场景分布概率相近的最优场景集,最大保留输入变量随机性特征.具体步骤包括: 1) 生成基于预测模型的场景.以风速vt为例,一种常见的自回归滑动平均模型表达式为[21] (19) 式中,p,q分别为自回归及滑动平均部分的阶数;{vt,vt-1,…,vt-p}为vt的时间序列;φp,φq为自回归系数;{εt,εt-1,…,εt-q}为误差序列.上述自回归系数、误差序列通过拟合实际历史数据获得.利用Monte Carlo抽样获得初始风速场景集Sr. 2) 削减提高描述效率的场景.在生成的初始风速场景集合Sr中,k(k∈[t,t+NΔt])时刻场景ωi,k与场景ωj,k之间的距离为 (20) 最大削减策略要求缩减前后场景集之间的概率距离最小,删除的场景集Ω需符合削减精度σ约束,即 (21) 实现式(13)的同步回代场景削减过程步骤如下: ① 初始化参数,迭代次数为m,第m次迭代计算时被删除的场景集记为Ωm,其中,Ω0为空集. ③ 判断步骤②中获得的最小值是否大于削减精度σ,若大于,则返回步骤②,m=m+1;若小于等于σ,则迭代停止,进入下一步骤. ④ 被删除的场景由保留场景集中距离最近的场景代替,保留场景的概率相应修正为能删除场景概率与保留场景的原概率之和. 相似地,光伏出力、电负荷、热负荷的场景Sv,Se,Sh生成、削减原理与网速Sr相同. 多随机变量场景的合并使得场景总数急剧增加,为进一步加快求解速度、提高能量管理在线求解能力,引入Benders分解.作为求解大规模问题的并行计算方法,Benders分解将原问题拆分为一个主问题及若干子问题,交互迭代,判断所得优化解是否为可行解,若优化解不是可行解,则向主问题返回一个“Benders割”,重新优化,迭代至找到符合收敛条件的最优解[22].具体如下: ① 初始化.记迭代次数b=1,Benders割θ初始赋值0,收敛条件上界U=+∞,下界L=-∞,主问题M、第s个场景下子问题Ss表达式为 (22) (23) (24) (25) (26) ④ 判断收敛条件为U-L≤ξ,ξ为预设的小常数;若收敛条件成立,则得到最优解;否则,迭代b+1次后返回步骤②. 以一个RES渗透率较大的区域IES为例验证能量管理模型.因RES出力与天气密切相关,取典型晴、阴天气连续工作日,光伏、风机输出随机性预测及实际出力如图4(a)所示,电、热负荷随机性预测及实际曲线如图4(b)所示.引入场景削减与Benders分解以加快求解,故与文献[16]不同,预测场景区间内设置大量初始场景.设可切除负荷不超过10%,电价考虑峰谷平电价,天然气价格在仿真时域内认为恒定. 区域IES内元件参数如下:微型燃气轮机Pcmin=1.5 MW,Pcmax=3 MW,ηc=0.8,ηce,t=0.3~0.4;燃气锅炉最大功率为Plmax=2.5 MW,ηl=0.85;EHP最大功率为Phmax=1 MW,ηh=0.9;电池储能系统Emin=0.3 MW·h,Emax=1.5 MW·h,Pbcmax=Pbdmax=0.3 MW,ηb=0.99,ηbc=ηbd=0.95;蓄热水罐Cmin=0.4 MW·h,Cmax=2 MW·h,Pwcmax=Pwdmax=0.8 MW,ηw=0.95,ηwc=ηwd=0.9.IES中充电桩共计300台,额定功率都为7 kW.电动汽车出行规律包括抵达时间、离开时间、行驶里程,抵达时间近似服从正态分布N(9,0.52)和N(18,1.52),离开时间近似服从正态分布N(19,1.52)和N(7,0.52),行驶里程近似服从对数正态分布.假设用户设置的Ez,set都为100%. (a) RES预测场景及实际出力 (b) 电负荷、热负荷预测及实际需求曲线 为综合比较本文提出方法的优化结果与在线运行时间,定义并仿真下述3种方法:① 不考虑滚动与随机优化的RBC(rule-based control)方法,即不考虑预测时域、所有指令仅围绕当前时刻能量平衡及设备约束条件,相当于式(17)中取N=0,Ns=1,ps,k=1.② 考虑滚动优化、但仅考虑确定等值预测的DMPC方法,相当于式(17)中N分别取3,5,Ns=1,ps,k=1.③ 未采用综合利用场景削减与Benders分解的O-SMPC(original SMPC)方法.④ 本文方法SMPC.在Intel i3 CPU,4GB RAM环境下仿真. 令Δt=1 h,预测步长分别为3,5和7,比较上述4种方法在48 h内的运行成本和计算速度,见表1.从经济性方面比较,RBC方法的支出最高,3种MPC方法可以明显降低IES总运行成本.考虑了随机性的SMPC和O-SMPC的2种方法比未考虑随机性的DMPC,运行成本进一步降低,经济性提高;而SMPC与O-SMPC运行成本非常接近.从计算速度方面比较,从表1中选取的仿真时段内出现的单次最大计算时间可以看出,包含大量随机场景的O-SMPC方法其变量数量远大于RBC和DMPC,运行速度明显放缓.而在采用本文提出的含场景削减与Benders分解的SMPC方法后,周期内最大单次计算时间较为理想. 表1 能量管理方法经济性与计算速度 上述分析表明,本文方法在利用随机优化实现经济性的同时,又通过加快求解策略使计算成本未发生显著增加.这是由于一方面在输入层面通过场景削减减少场景总数;另一方面,在求解层面引入的Bender分解可以充分利用并行计算,使求解效率得到提升.总的来说,在同样的信通设备、计算配置等基础设施下,本文方法经济性更好,当预测步长适中时,每次计算耗时可控制在合理的数量级,不影响能量管理在线运行. 以下基于预测步长N=5进行分析.电动汽车有序充电的执行情况如图5所示,可以看出,能量管理策略在满足总充电需求的前提下,部分充电行为被引导为延期执行.因基于经济性的有序充电将引导充电负荷避开高峰电价时段,因此又起到削减用电高峰负荷的作用.随着电动汽车数量的逐渐增加,有序充电的意义将更突出. 图5 有序充电前后的电动汽车充电总负荷曲线 每个Δt内IES运行支出及电、热子网络供需平衡如图6(a)~(c)所示,记支出为正.因算例RES安装容量较高,即随机变量占比较大,在光伏出力较多的晴天日中时段(如首日9:00—16:00),IES售电获得盈利,目标函数根据RES出力与负荷预测时域内的趋势,选择午间售出电量;随着预测时域内负荷增加,RES出力降低,结合电价变化,转以蓄能为主,以提前应对晚间用电高峰.次日阴天时,光伏出力急剧下降,RES出力转以满足自用为主,售电时长与收益均明显降低(如次日10:00—11:00).此外,IES中微型燃气轮机、EHP等耦合元件使子网络间的能量分配相互影响,较单一能流系统更复杂,如当早晚负荷即将出现高峰、电价即将进入峰时段前,或RES出力因气象因素降低时,要综合考虑启停成本,微型燃气轮机应适时启动,并结合负荷变化,适当调整电热转换的比例,使得子网络能量供应更灵活、设备利用率更高. (a) 区域综合能源系统各时段支出与累积支出 (b) 电力子网络供需平衡 (c) 热力子网络供需平衡 1) 提出了一种基于随机优化的综合能源系统能量管理策略,不仅考虑了电、热、气等常见的子系统,还包含了以电动汽车为代表的绿色交通子系统给综合能源系统带来的新用电负荷. 2) 由于考虑了可再生能源出力等预测模型的随机性,为满足能量管理策略在线求解的速度需要,本文综合采用了场景削减技术和Benders分解2种方法,使得引入随机优化在提高能量管理经济性的同时,对计算速度的影响降至最低. 3) 针对电动汽车有序充电策略,设计了以充电桩为控制对象的控制策略,又通过采样并生成预测充电序列的方法,解决了由于汽车流动性导致的模型预测控制应用时时长不一致的问题. ) [1] Pan Z, Guo Q, Sun H. Interactions of district electricity and heating systems considering time-scale characteristics based on quasi-steady multi-energy flow[J].AppliedEnergy, 2016,167: 230-243. DOI:10.1016/j.apenergy.2015.10.095. [2] 王伟亮, 王丹, 贾宏杰, 等. 能源互联网背景下的典型区域综合能源系统稳态分析研究综述[J]. 中国电机工程学报, 2016, 36(12): 3292-3306. DOI:10.13334/j.0258-8013.pcsee.152858. Wang Weiliang, Wang Dan, Jia Hongjie, et al. Review of steady-state analysis of typical regional integrated energy system under the background of energy internet[J].ProceedingsoftheCSEE, 2016,36(12): 3292-3306. DOI:10.13334/j.0258-8013.pcsee.152858.(in Chinese) [3] Mancarella P. MES (multi-energy systems): An overview of concepts and evaluation models[J].Energy, 2014,65: 1-17. DOI:10.1016/j.energy.2013.10.041. [4] 孙宏斌, 潘昭光,郭庆来. 多能流能量管理研究:挑战与展望[J]. 电力系统自动化, 2016, 40(15): 1-8 ,16. DOI:10.7500/AEPS20160522006. Sun Hongbin, Pan Zhaoguang, Guo Qinglai. Energy management for multi-energy flow: Challenges and prospect[J].AutomationofElectricPowerSystems, 2016,40(15): 1-8 ,16. DOI:10.7500/AEPS2016 0522006. (in Chinese) [5] Liu M, McNamara P, Shorten R, et al. Residential electrical vehicle charging strategies: The good, the bad and the ugly[J].JournalofModernPowerSystemsandCleanEnergy, 2015,3(2): 190-202. DOI:10.1007/s40565-015-0122-2. [6] Mayne D Q. Model predictive control: Recent developments and future promise[J].Automatica, 2014,50(12): 2967-2986. DOI:10.1016/j.automatica.2014.10.128. [7] 席裕庚, 李德伟, 林姝. 模型预测控制——现状与挑战[J]. 自动化学报, 2013, 39(3): 222-236. Xi Yugeng, Li Dewei, Lin Shu. Model predictive control: Status and challenges [J].ActaAutomaticaSinica, 2013,39(3): 222-236. (in Chinese) [8] Khan A A, Naeem M, Iqbal M, et al. A compendium of optimization objectives, constraints, tools and algorithms for energy management in microgrids[J].RenewableandSustainableEnergyReviews, 2016,58: 1664-1683. DOI:10.1016/j.rser.2015.12.259. [9] 薛禹胜, 郁琛, 赵俊华, 等. 关于短期及超短期风电功率预测的评述[J]. 电力系统自动化, 2015, 39(6): 141-151. DOI:10.7500/AEPS20141218003. Xue Yusheng, Yu Chen, Zhao Junhua, et al. A review on short-term and ultra-short-term wind power prediction[J].AutomationofElectricPowerSystems, 2015,39(6): 141-151. DOI:10.7500/AEPS2014 1218003. (in Chinese) [10] 马瑞, 李文晔, 李晅, 等. 分布式冷热电联供系统负荷随机模糊建模[J]. 电力系统自动化, 2016, 40(15): 53-58. DOI:10.7500/AEPS20151021001. Ma Rui, Li Wenye, Li Xuan, et al. Random fuzzy model for load of distributed combined cooling, heating and power system[J].AutomationofElectricPowerSystems, 2016,40(15): 53-58. DOI:10.7500/AEPS20151021001. (in Chinese) [11] 张洪财, 胡泽春, 宋永华,等. 考虑时空分布的电动汽车充电负荷预测方法[J]. 电力系统自动化, 2014, 38(1): 13-20. DOI:10.7500/AEPS2013 0613009. Zhang Hongcai, Hu Zechun, Song Yonghua, et al. A prediction method for electric vehicle charging load considering spatial and temporal distribution[J].AutomationofElectricPowerSystems, 2014,38(1): 13-20. DOI:10.7500/AEPS20130613009. (in Chinese) [12] Mesbah A. Stochastic model predictive control: An overview and perspectives for future research[J].IEEEControlSystemsMagazine, 2016,36(6): 30-44. DOI:10.1109/mcs.2016.2602087. [13] Patrinos P, Trimboli S, Bemporad A. Stochastic MPC for real-time market-based optimal power dispatch[C]//IEEEConferenceonDecision&Control&EuropeanControlConference. Orlando, USA, 2011: 7111-7116. [14] 张彦, 张涛, 刘亚杰, 等. 基于随机模型预测控制的能源局域网优化调度研究[J]. 中国电机工程学报, 2016, 36(13): 3451-3462,3364. DOI:10.13334/j.0258-8013.pcsee.152491. Zhang Yan, Zhang Tao, Liu Yajie, et al. Stochastic model predictive control for energy management optimization of an energy local network[J].ProceedingsoftheCSEE, 2016,36(13): 3451-3462,3364. DOI:10.13334/j.0258-8013.pcsee.152491. (in Chinese) [15] Su W, Wang J, Roh J. Stochastic energy scheduling in microgrids with intermittent renewable energy resources[J].IEEETransactionsonSmartGrid, 2014,5(4): 1876-1883. DOI:10.1109/tsg.2013.2280645. [16] Wang Y, Zhou Z, Botterud A, et al. Stochastic coordinated operation of wind and battery energy storage system considering battery degradation[J].JournalofModernPowerSystemsandCleanEnergy, 2016,4(4): 581-592. DOI:10.1007/s40565-016-0238-z. [17] Kou P, Liang D, Gao L, et al. Stochastic coordination of plug-in electric vehicles and wind turbines in microgrid: A model predictive control approach[J].IEEETransactionsonSmartGrid, 2016,7(3): 1537-1551. DOI:10.1109/tsg.2015.2475316. [18] Parisio A, Rikos E, Glielmo L. Stochastic model predictive control for economic/environmental operation management of microgrids: An experimental case study[J].JournalofProcessControl, 2016,43: 24-37. DOI:10.1016/j.jprocont.2016.04.008. [19] Zheng Q P, Wang J, Liu A L. Stochastic optimization for unit commitment: A review[J].IEEETransactionsonPowerSystems, 2015,30(4): 1913-1924. DOI:10.1109/tpwrs.2014.2355204. [20] Growe-Kuska N, Heitsch H, Romisch W. Scenario reduction and scenario tree construction for power management problems[C]//IEEEPowerTechConferenceProceedings. Bologna, Italy,2003: 3-7. [21] Morales J M, Mínguez R, Conejo A J. A methodology to generate statistically dependent wind speed scenarios[J].AppliedEnergy, 2010,87(3): 843-855. DOI:10.1016/j.apenergy.2009.09.022. [22] Benders J F. Partitioning procedures for solving mixed-variables programming problems[J].NumerischeMathematik, 1962,4(1): 238-252. DOI:10.1007/bf01386316.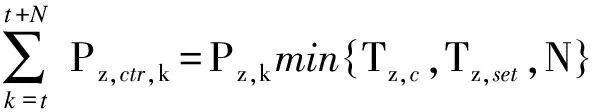
2 基于随机优化的能量管理策略
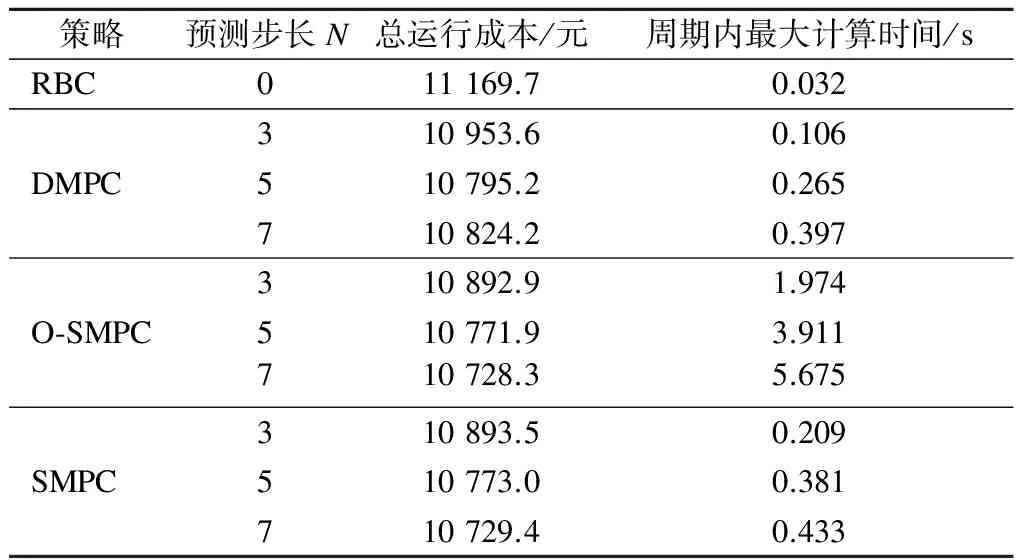
2.1 基于随机模型预测控制的能量管理模型
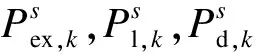
2.2 随机变量的场景树技术


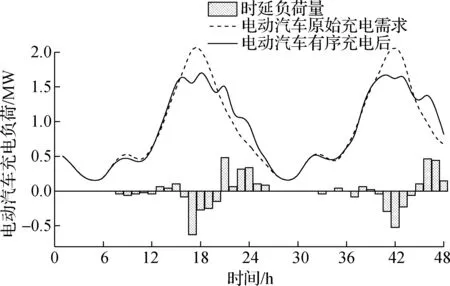
2.3 基于Benders分解的快速求解




3 算例
3.1 算例参数
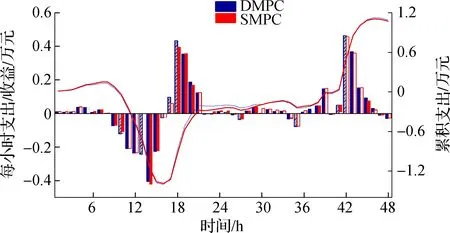
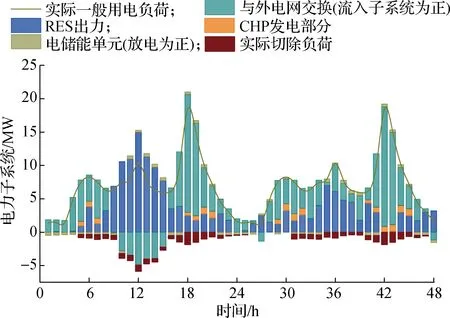
3.2 仿真与分析

4 结论

