基于贝叶斯网络的人才培养模式绩效评价

柳炳祥，田 原，彭永康，邱 娟

（景德镇陶瓷大学 信息工程学院，江西 景德镇 333403）

0 引 言

目前，教育部在全国高校中开展“审核评估”[1]，通过评估学校内部质量保障体系对学校办学质量进行间接评估，从而促进学校的“五个度”（对学校人才培养效果与培养目标的达成度、学校办学定位和人才培养目标与社会需求的适应度、教师和教学资源对学校人才培养的保障度、教学质量保障体系运行的有效度、学生及用人单位的满意度），并提高学校的“三强化”（强化办学合理定位、强化教学中心地位、强化内部质量保障体系建设）。一般地方高校在转型发展的新形势下，如何科学、合理地设计人才培养目标，将人才培养模式绩效评价工作融入“审核评估”的框架内，是需要进一步研究的问题。

1 用于人才培养模式绩效评价的贝叶斯网络构建

在处理不确定性问题的模拟和推理时，贝叶斯网络[2]是一种被广泛使用的工具，可以通过不断地自我学习调整网络结构和概率分布，从而识别出观测变量之间的因果关系及关联强度，并且这种关联性可以通过简洁的图模型表示出来，其所包含的语义便于解释、易于理解。

贝叶斯网络是一个有向无环图，定义为：给定一个随机变量集合χ={x1,x2……xn}，其中xi是一个m维向量，贝叶斯网络B=＜G,θ＞，其中G为网络结构，θ为网络参数，G可以看做问题领域的定性描述，θ看做定量描述。θ通常称为条件概率表，描述每个结点在其父结点取所有可能值情况下的条件概率。贝叶斯网络学习的任务是从样本数据中学习网络结构和各结点的条件概率表。

1.1 人才培养模式绩效评价模型的构建

为了使评价模型在全面和实用之间做到平衡，教师需要合理设计评价指标体系，可以从3方面考虑：人才培养的基础条件、人才培养过程及人才培养质量反馈，据此设计的人才培养模式绩效评价指标体系[3]见表1。笔者首先所做的工作是将指标体系映射为贝叶斯网络，这一步采用人工构造方法，将指标体系中的三级指标作为贝叶斯网络中的根结点，二级指标由一级指标确定，三级指标由二级指标确定，由此设计出指标体系的贝叶斯网络模型拓扑结构图，可以体现出各级指标之间的因果关系。该模型中除了包含指标体系中的所有指标外，还有一个结点PE用来表示每个专业班级的最终绩效水平分数。

指标体系中每个评价指标的量纲不同，原始评价数据需处理成统一的量纲，其中一级指标是定量指标，需转换成等级表示，二级指标和三级指标是定性指标的等级表示，无需再转换，因此所对应的贝叶斯网络的结点设计为离散结点。对应评价指标的等级，每个结点由5种状态组成：5代表优秀， 4代表良好， 3代表中等， 2代表一般，1代表较差。

表1 专业人才培养模式绩效评价三级指标体系

1.2 评价指标之间因果关系的确定

贝叶斯网络中结点之间的因果关系采用条件概率表的形式描述。当贝叶斯网络的结构确定之后，接下来的工作是确定贝叶斯网络的参数，即结点的条件概率表。贝叶斯网络的参数学习有多种方法，我们采用的是极大似然估计法（ML）[4]。样本数据在经过预处理后，已全部表示为前述5个等级形式的离散数据。对于给定的贝叶斯网络B，在条件概率分布为离散形式的情况下，则可采用基于频率的学习方法。若其某个结点Xi有ri个取值1、2、3……ri，其父结点集π（Xi）取值有qi个组合1、2、3……qi，则该网络的参数而似然函数为

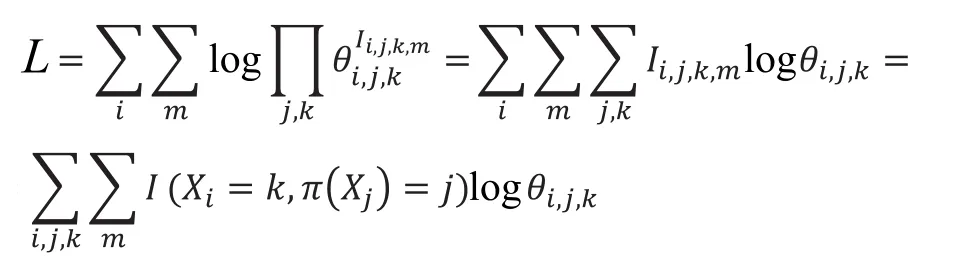
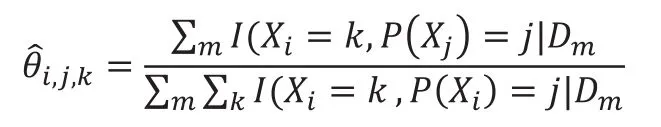
据此，将样本数据划分为训练集和测试集，用训练集数据对网络进行训练，求出各结点的条件概率表。各级指标结点的条件概率表的形式见表2，B1的父结点为C1、C2和C3，每个结点的离散取值范围为1～5。

表2 结点B1的条件概率表（部分）

1.3 贝叶斯网络人才培养绩效评价模型的验证

接下来，用测试集数据验证贝叶斯网络人才培养绩效评价模型，将测试集的每个样本作为证据变量输入该模型中。由于模型的输出结果为概率分布表，故选取概率值最大的量作为模型的预测值。测试结果表明该模型的正确率为72%。

2 基于贝叶斯网络对人才培养模式进行绩效评价

贝叶斯网络建立之后，优点是可以对不完备数据进行推理和不确定推理。给定部分结点的证据数据即可推理出所需其他结点的概率分布，因此可以很好地应对数据不完备的情况。以本校信息管理与信息系统专业为例，取5个年级{A、B、C、D、E}的样本数据作为证据，输入已经训练好的贝叶斯网络，求出各样本数据PE结点的等级值，再按年级求PE结点的概率分布，结果见表3。可见，按此方法进行评价，结果基本分布在等级3，即中等这个级别。通过对结果进一步分析，应给出相应对策，如调整人才培养目标、加强学风建设和专业建设力度等。

表3 各年级评价结果的概率分布

3 结 语

科学评价专业人才培养模式，对于高校各专业自主设定人才培养目标和规划人才培养路径具有正向促进作用，且容易激发高校在人才培养方面的主动性和创造性。专业人才培养模式绩效评价的常态化和开放化，有利于落实高校自主办学。

[1]中华人民共和国教育部. 教育部关于开展普通高等学校本科教学工作审核评估的通知[EB/OL]. (2013-12-05)[2017-08-09].http://www.moe.edu.cn/publicfiles/business/htmlfiles/moe/s7168/201312/xxgk_160919.html.

[2]Microsoft. A tutorial on learning bayesian networks[EB/OL]. (1995-03-01)[2017-08-09]. https://www.microsoft.com/en-us/research/publication/a-tutorial-on-learning-with-bayesian-networks/.

[3]Kim S, Imoto S, Miyano S. Dynamic bayesian network and nonparametric regression for nonlinear modeling of gene networks from time series gene expression data[J]. Biosystems, 2004, 75(1): 57-65.

[4]田原, 张俊娜, 贾建华,等. 信息管理与信息系统专业人才培养模式绩效评价研究[J]. 科教文汇旬刊, 2015(5): 67-68.

[5]Spiegelhalter D J, Lauritzen S L. Sequential updating of conditional probabilities on directed graphical structures[J]. Networks,1990, 20(5): 579-605.