物体在不可压缩流场中所受的流体动力表达式

林新武,林献武,兰维瑶

(厦门大学航空航天学院,福建厦门361005)

平流层飞艇用作高空信息平台时,与空基平台相比具有低能耗、驻留时间长和覆盖区域广的优点;与天基平台相比又具有距离地面近、观察时间长、发射和维护成本低的优点,可成为空基和天基信息平台的有益补充．由于平流层飞艇的这种诱人应用前景,近10多年来,许多国家投入了大量的人力物力研究平流层飞艇技术,并取得了一些进展．作为一种飞行器,气动力仍然是平流层飞艇技术的一个研究重点;同时,飞艇作为一种平均密度与周围流体密度接近的飞行器,人们往往认为其飞行过程受到非定常气动力的影响超过传统的重飞行器[1]．

Lamb等[2]总结并完善了在不考虑粘性的情况下非定常气动力的计算方法．由于粘性对气动力具有重要的影响作用,许多研究者[3-7]经过不懈的努力，发展了一套飞艇气动力的工程估算方法．他们的主要思想是利用圆柱比拟的方法来估计艇体的定常升力,用平板气动力或薄弹翼理论来估算尾翼的气动力,用等效附加攻角的思想来估算飞艇非定常运动时的气动力,用翼体干扰因子来考虑组合体气动力与翼体单独气动力之和的差异．该工程方法后来被许多研究者引用和完善[1,8-11],然而它缺乏坚实的理论基础并且只能估算小部分非定常气动力,大部分的非定常气动力如附加质量和附加惯量等仍需要采用Lamb等[2]所提供的无粘流结果，因此人们期待一种能计算有粘流非定常气动力的方法．

著名的涡动力学学者Wu[12-13]针对有粘流不可压缩流场提出了一种流体动力表达式,该理论与Lamb的理论[2]区别在于其采用了有粘流假设，这种处理方法考虑了真实流体对能量的耗散性，更加符合实际情况.其相关理论后来在Wu等[14-15]的一些专著中不断得到完善,也被其他学者改进和演绎[16-17],为有粘不可压缩流情况下的运动体气动力计算提供了理论依据．然而在应用这个表达式计算运动体非定常气动力时存在如下困难:1) 在去除流场粘性的情况下,基于涡动力学理论的气动力表达式与Lamb的无粘流气动力表达式并不一致,其他学者也注意到这种情况,即有粘流中的附加质量表达式与无粘流的情况不同[16];2) 使用涡动力学理论计算运动体气动力时,需要计算速度在运动体所占领空间上的积分,但这个速度场的具体概念并不明确,一般认为是运动体上对应刚体质点的速度.若按这种概念来理解就会导致一个悖论,即空心或内部含多刚体结构的运动体与实心运动体的气动力不同．出现这种现象的根本原因在于这个流体动力表达式的推导过程中或多或少地将运动体所占领的空间和流体所占领的空间视为一体．事实上,流体动力与刚性运动体的内部结构并无关系,因此本研究尝试仅针对流体进行分析来获得不可压缩流场中的运动体流体动力表达式．这种表达式不但与运动体的内部结构无关,而且在无粘流情况下收敛于Lamb的结果,在有粘流场的情况下与涡动力学理论的结果一致,为人们进一步理解不可压缩流场的特点提供理论参考．

1 流体动力表达式

对于不可压缩流场,其速度v控制方程为[13]

(1)

(2)

其中：式(1)为连续性方程,式(2)为Navier-Stokes方程或动量方程;ρ,p,ν分别是流体的密度、压力和运动粘性系数；式(2)中已略去保守力如重力等．定义涡量为速度的旋度[16]

(3)

由于不可压缩流场中ρ为常数,则对动量方程(2)两边同求旋度可得涡量传输方程

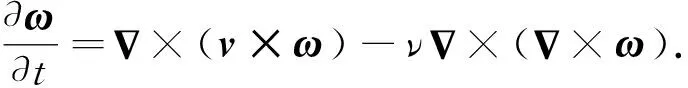
(4)

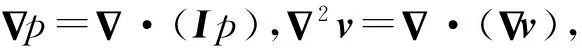
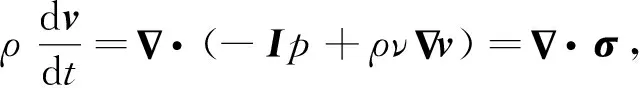
(5)

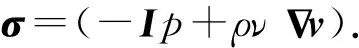
记运动体所占领的空间区域为Rb,其边界记为Sb,与Sb接触的流体表面记为Si,Sb和Si的空间形状和位置是完全一致的．对于有粘流而言,根据无滑移边界条件，Sb和Si上的对应点速度是一致的；对于无粘流而言,滑移边界条件将使得Sb和Si上的对应点速度出现差异．在流场空间中取一个位置固定的封闭曲面Se使得其包含Rb和部分流体,且位于Si和Se之间流体所占领的空间区域记为Rf．取Rf中的流体作为研究对象,将式(5)在Rf上积分并利用张量形式的高斯公式可得积分形式的流场动量定理[18]

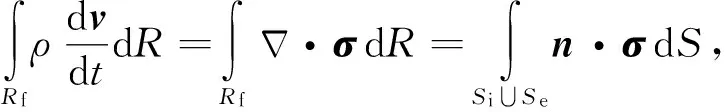
(6)

其中，n表示Si∪Se的法向量,指向Rf外部为正．

式(6)最后一项在Si上的积分结果就是运动体所受流体动力F的反作用力,因此

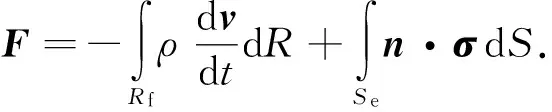
(7)

先讨论式(7)等号右端的第1项．考虑到Rf不是控制体,则根据文献[18]中的研究结果,对于不可压缩流场Rf有

(8)

其中vs为边界Si∪Se的运动速度．由于Se是固定的,因此在Se上vs=0;在Si上,由于流体没有进出物面,因此(vs-v)·n=0．这样,式(8)可简化为

(9)

根据文献[14],有如下导数矩转换(derivative moment transformation,DMT)公式

(n(t)×f) dS,

(10)

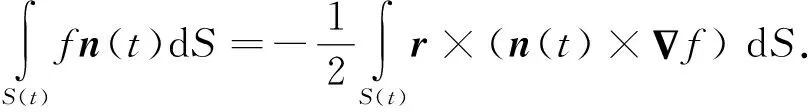
(11)

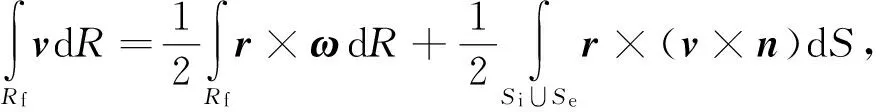
(12)

合并上式和式(9)得

(13)

现在讨论式(7)等号右端的第2项．根据Wu[12-13]的理论,在有限时间内,涡量场随距离物面长度的增加以指数形式衰减,令Se离物面足够远,这时其附近流场可视为无旋,根据式(5)可知

(14)

(15)

由于Rps是任意选取的,为了使上式在Rp中恒成立,必须有n·σ=-pn，于是式(7)等号右端的第2项可写为

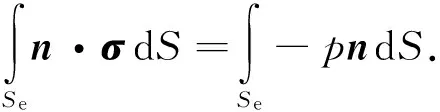
(16)

令式(11)中的积分区域取S(t)=Se,f取流场静压力p,则

(17)

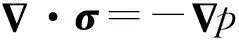
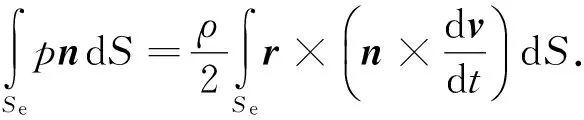
(18)

(19)

(20)

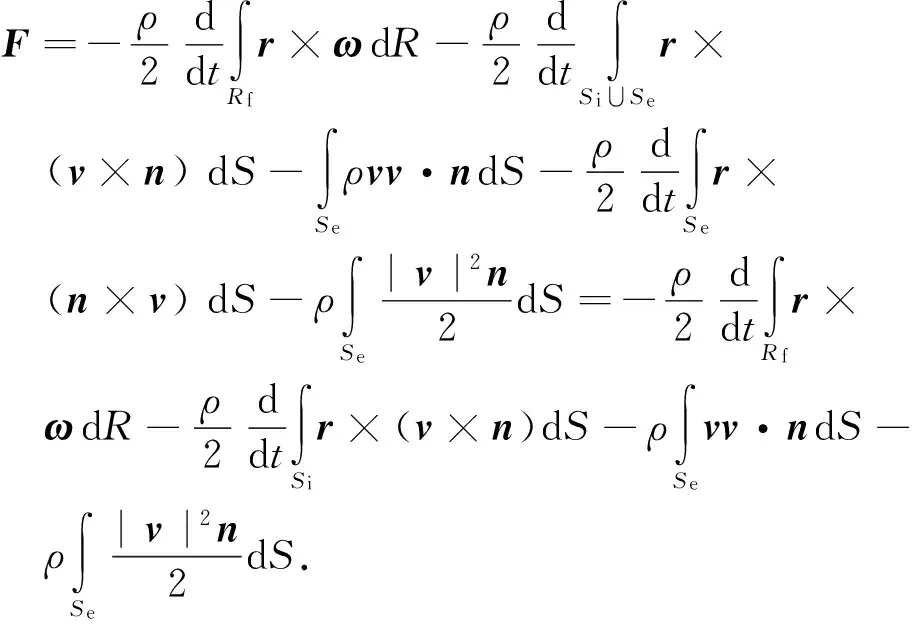
(21)

最后根据速度在远场的渐进特性[20],式(21)等号右边在Se上的积分结果为0,于是得流体动力的最终表达式为

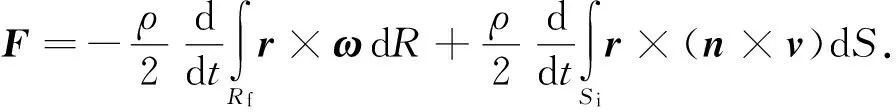
(22)

(23)

上式成立的条件为v在Rb和Si上连续,其中第2项改变了符号是为了使n的方向与式(6)中n的方向保持一致,即指向Rf外部为正．合并上述两式可得

(24)

Rb上的v和ω是虚拟存在且不确定的,仅需保证v在Rb和Si上连续．对于有粘流而言,一个符合此条件的v分布是将运动体视为实心刚体,这样上式的结果就是Wu[13]所给出的有粘不可压缩流场气动力表达式．如果运动体是空心的,或者运动体内部出现多刚体结构,则v的分布仍可按实心刚体来计算,说明运动体是气动力与其内部的结构无关,符合事实．

如果流场是无粘的,则不能将Rb上的v用实心刚体所对应的速度场来替代,这是因为滑移边界条件导致这种处理方法并不能保证v在Si上连续．这时需要根据Si上的v来重新确定其在Rb上的分布以保证连续性．这里给出一种确定Rb上v和ω的具体方法:有一个不渗透的壳体,其形状与Si一致且壳体上各质点的速度分布等于流场在Si上的速度分布;然后往壳体内部注入含磁性物质的粘性流体,利用电磁力使壳体内部的流体运动起来,这时壳体内部流场所对应的v和ω就能满足Rb以及Si上的连续性要求．当电磁力和时间不同时,壳体内部的流场分布也是不同的,这意味着虚拟涡的分布并不是唯一的．然后将得到的Rb上的v和ω的分布代入式(24)来计算气动力；或者,更简单地,直接根据式(22)来计算气动力．

在上面的推导结果中,Rf的外边界处于无穷远处,而在实际应用中只能够取到有限区域,这将导致一定的计算误差．对于实际飞行器的运动过程中,其运动时间总是有限的,因此满足Wu所设定的条件[12]．于是,涡量的强度随着与物面的距离增加以指数规律衰减．指数衰减要比幂级数衰减更快,因此在实际应用中,并不需要取太大的空间区域即可达到足够的计算精度．

2 与无粘流气动力表达式的兼容性

(25)

其中F为运动体所受到的流体动力．对于不可压缩无粘流场而言,Lamb根据能量守恒定律证明了[2]

(26)

其中u,v,w为运动体速度vb的3个分量,T表示Rf中流体所包含的动能．由于流场动能可根据流场的速度分布来确定,因此Iimp和F均可通过实际计算得到．

由此可见,Lamb在推导无粘流气动力表达式时并没有用到流场的动量和流场的动量定理．为了证明式(24)兼容Lamb的流体动力表达式,需要建立Lamb方法与动量定理之间的关系．记流场的总动量

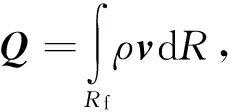
(27)

则根据物理学中的冲量定理,流场的总动量等于外力冲量之和,它不但包括运动体所提供的冲量,也包括Se上流场压力p所产生的冲量,因此

(28)

(29)

上式和基于流场动量定理得到的流体动力表达式(7)是一致的,因此式(24)兼容于Lamb给出的结果即式(25)．从式(29)还可以看出,Lamb利用冲量的概念巧妙地回避了无穷远边界上的压力计算问题．但他所提出的基于流场动能计算冲量的方法,即表达式(26)仅在无粘流场中成立,难以推广到存在粘性和能量耗散的有粘流场,这是其局限性．

3 算 例

式(22)和(24)在有粘流场中的等效性已被Wu[13]证明，式(24)的正确性,也在文献[12]中有所论述和验证,因此这里将仅讨论式(22)与无粘流场中Lamb理论的等效性.以圆球在静止无粘流场中直线运动的附加质量为例来进行讨论．

由文献[2]可知,无粘流场中直线运动圆球的速势为

(30)

其中U为球直线运动速度的大小,a为球的半径,r、θ为球面坐标．那么在以球心为原点的固连直角坐标系中,令

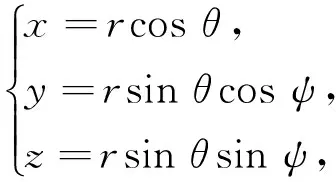
(31)

其中θ∈[0,π],ψ∈[0,2π]，则可得

(32)

将式(32)代入式(30)中可得圆球速势在直角坐标系中的表达式如下:

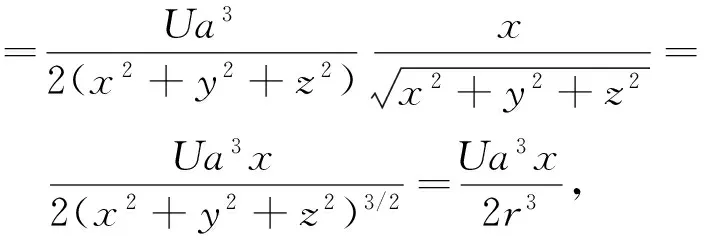
(33)

于是流场速度在直角坐标系下的速度分量为

(34)

又圆球表面位矢r及法向量n分别如下:

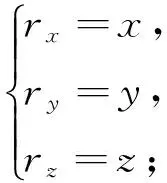
(35)

(36)

进而可将式(34),式(35)和式(36)代入式(22)来计算无粘流场中圆球直线运动气动力,由于无粘流场中ω为0,可得无粘流场中圆球直线运动气动力为

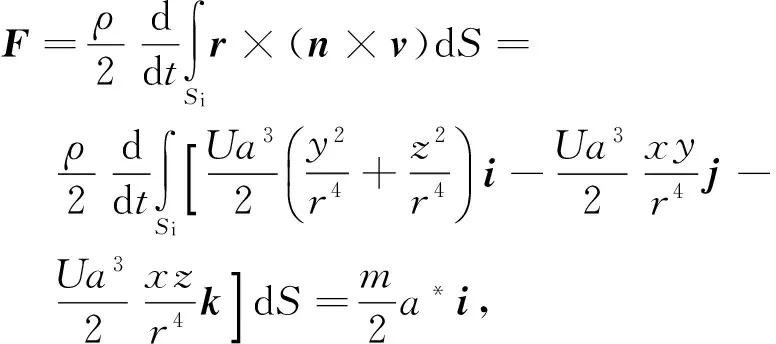
(37)

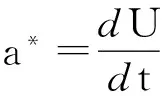
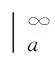
(38)

4 结 论

本研究在流场Rf上速度分布连续的基础上重新推导了运动体在不可压缩流体中运动时所受的气动力．由于回避了流体在物面边界上的连续性问题,所得的公式不仅适用于有粘流场,也适用于无粘流场．研究结果表明,涡动力学理论所给出的式(24)在实际应用中,运动体所占领空间Rb上速度场分布并非唯一,但需要在保证内部连续的同时与Rf中的速度分布在Si上连续．对于有粘流而言,这种速度分布可以取实心刚体上的速度场；对于无粘流而言,由于滑移边界条件,实心刚体所对应的速度场并不一定能满足v在Si上的连续性,这时可直接采用式(22)来计算气动力．

[1] KHOURY G A,GILLETT J D.Airship technology[M].2nd ed.New York:Cambridge University Press,2012:36-38.

[2] LAMB H.Hydrodynamics[M].6th ed.New York:Dover,1945:160-201，214.

[3] ALLEN H J.Estimation of the forces and moments acting on inclined bodies of high fineness ratio,RM-A9I26[R].Washington D C:NACA,1949.

[4] ALLEN H J,PERKINS E W.A study of effects of viscosity on flow over slender inclined bodies of revolution,REPORT1048[R].Washington DC:NACA,1951.

[5] HOPKINS E J.A semi-empirical method for calculating the pitching moment of bodies of revolution at low Mach numbers，RM-A51C14[R].Washington DC:NACA,1951.

[6] JONES S P,DELAURIER J D.Aerodynamic estimation techniques for aerostats and airship[J].Journal of Aircraft,2015,20(2):120-126.

[7] 基里林·阿列克桑徳拉·尼卡拉伊维奇.现代飞艇设计导论[M].吴飞,王培美,译.北京:国防工业出版社,2009：5-26.

[8] MUELLER J B,PALUSZEK M A,ZHAO Y Y.Development of an aerodynamic model and control law design for a high altitude airship[C]∥AIAA 3rd "Unmanned Unlimited" Technical Conference.Chicago:Workshop and Exhibit,2004:1-17.

[9] LI Y,NAHON M.Modeling and simulation of airship dynamics[J].Journal of Guidance Control & Dynamics,2007,30(6):1691-1700.

[10] LI Y,NAHON M,SHARF I.Airship dynamic modeling:a literature review[J].Progress in Aerospace Sciences,2011,47(3):217-239.

[11] SEBBANE Y B.Lighter than air robots[M].Netherlands:Springer,2012：34.

[12] WU J C.Theory for aerodynamic forces and moments in viscous flow[J].AIAA Journal,2012,19(4):432-441.

[13] WU J C.Elements of vorticity aerodynamics[M].Shanghai:Shanghai Jiaotong University Press,2014:12,51,78,83-89,93.

[14] WU J Z,MA H Y,ZHOU M D.Vorticity and vortex dynamics[M].Berlin Heidelberg:Springer,2006：600-603.

[15] WU J Z,MA H Y,ZHOU M D.Vortical flows[M].Berlin Heidelberg:Springer,2015：312-320.

[16] 吴子牛.空气动力学(下册)[M].北京:清华大学出版社,2008：85.

[17] 童炳刚,尹协远,朱克勤.涡运动理论[M].合肥:中国科学技术大学出版社,2009：69.

[18] 林献武,兰维瑶,李智斌,等.时变系统流场动量定理的积分形式及其在流体动力系数分析中的应用[J].应用数学和力学,2016,37(6):551-566.

[19] 易中,吴萱,周丽珍.低速空气动力学[M].北京:冶金工业出版社,2005：9.

[20] BATCHELOR G K.An introduction to fluid dynamics[M].Beijing:China Machine Press,2014:114-117.