一种高效的基于教与学的社区发现算法
李佩茜,冯少荣
(厦门大学信息科学与技术学院,福建厦门361005)
现实世界有许多复杂网络体系,例如社交网络、生物网络、万维网等.在数学与计算机领域中,复杂网络被定义为图,包括一系列的节点与连接节点的边,节点代表个体,边代表个体与个体之间的联系.一般而言,社区是指复杂网络中联系较为紧密的子网络[1],社区发现就是为了找到复杂网络的内部特征,便于更加了解复杂网络中的内在信息.社区发现问题通过发现节点之间的相似度或其他相关属性,对复杂网络进行社区划分.它可以被看作是一种最优化问题[2].
基于教与学的最优化算法(TLBO)[3]是一种种群智能优化算法,分为两个阶段:1) 学生向老师学习(称为教学阶段);2) 学生之间的相互学习(称为学习阶段).通过这两个阶段的共同作用提高学生成绩.TLBO具有简单、易于理解、算法参数少、优化精度高和收敛速度快等优点,广泛运用于各个领域中的最优化问题[4-7].Keesari等[8]用TLBO解决车间作业调度问题,Xia等[9]提出简化的TLBO解决拆分序列问题,Baykasoglu等[10]分别分析了TLBO在流水车间(FSSP)与车间作业调度(JSSP)的表现.与此同时,Dede[11]把TLBO运用于离散化的桁架结构最优化问题,Li等[12]提出离散化TLBO解决流水车间调度问题.
从本质上来看,复杂网络中的社区发现问题是一种聚簇最优化问题.Chen等[13]提出了一种基于教与学的多目标社区发现算法(MODTLBO/D)来解决社区发现问题.该算法中,每个个体从邻居的平均值处进行学习,算法时间复杂度高,且在学习阶段,个体仅仅从邻居处进行学习,容易陷入局部最优.因此,本文中提出一种在多种群进化策略下的MODTLBO/D(E-MODTLBO/D).采用多种群并进的进化策略,在不同种群中采用不同的进化规则.在教学阶段,采用自适应学习因子;在学习阶段,每个个体在各自的子种群内可以采用随机学习策略或者是改进的量子行为学习策略.在每次迭代更新后,子种群间进行信息交流,维持算法的多样性与避免早熟收敛.把改进后的算法带入真实网络中进行实验发现,本文中提出的E-MODTLBDO/D算法在时间复杂度与发现高质量的社区结构方面比MODTLBO/D等算法表现更好.
1 社区发现
1.1 相关工作
近年来发现,很多现实世界的复杂系统可以由复杂网络来表示,发现复杂网络中的社区结构问题就是社区发现问题,该问题已经越来越受到人们的广泛关注.许多来自不同领域的算法被提出来解决社区发现问题,这些算法大致可以分为以下3类:
1) 基于图划分的算法:在这类算法中,节点通过预定义的方法被划分到不同社区,使得社区之间的连接尽可能少.Ezhilarasi等[14]提出一种基于图划分的算法,该算法定义社区之间连接与内在连接差异的评价函数,旨在最小化评价函数.Pothen等[15]利用拉普拉斯矩阵的特征进行社区划分,实现社区发现.但这两种方法都需要预先定义划分准则,最小化划分准则将会导致划分效果不佳.因此,又出现了一些其他准则,例如平均划分[16]、比率划分[17]、标准化划分[18]等.基于图划分的算法存在需预定义社区大小等规则的缺点,这表明该种算法并不是理想的社区发现算法.
2) 基于分层的算法:这类算法的核心思想是运用相似度度量不同节点对之间的相似程度来解决社区发现问题.分层算法包括凝聚分层算法和分裂分层算法.典型的凝聚分层算法是标签传播算法(LPA)[19].典型的分裂分层算法是由Girvan与Newman提出的GN算法[20].这些方法自然生成了网络的社区划分,但是它们需要一个停止的规则.
3) 基于模块度的算法:此类算法在社区发现问题中被广泛运用.模块度Q是由Newman等[1]提出的用来评价社区划分质量的评价函数.Fast Newman(FN)算法[21]是一个经典的模块度算法,该算法从一些独立的节点开始,用贪心策略将原始图的连接信息反复加入到图中,获得最大可能的模块度增长.Blondel等[22]提出一种快速多步贪心策略(BGLL)来实现模块度最优,找到最优社区划分.除此之外,有一些单目标进化算法[23-27]被用来最优化模块度Q.由于单目标算法存在分辨率限制等缺陷,还有许多多目标进化算法被提出,其中包括Shi等[28]提出的多目标社区发现算法(MOCD)、Pizzuti等[29]提出的多目标遗传算法(MOGA-Net)、Gong等[30]提出的基于分解的多目标遗传算法(MOEA/D-Net).与此同时,Gong等[31]还提出一种基于分解的多目标离散粒子群智能算法来解决社区发现问题.除此之外,还有一些多目标进化算法解决社区发现问题[32-36],它们都是同时最优化两个互相矛盾的目标函数实现社区发现.
1.2 社区定义
一个复杂网络可以抽象为一个图G=(V,E),其中V为节点的集合,E为连接节点的边的集合.在复杂网络中的社区是指具有密切关系的节点的集合[37],也就是说在社区内部节点连接紧密,而在社区之间节点连接稀疏.复杂网络中的社区发现问题是一个聚类问题,旨在把图G划分成若干子图Gi(i=1,2,…,k),满足∪1≤i≤kGi=G且∩1≤i≤kGi=φ.
1.3 评价指标
为了找到更好的社区划分与评价社区划分的质量,必须采用恰当的质量评价指标.本文中采用标准互换信息(normalized mutual information,NMI)与模块度Q这两个最常见的评价指标.近些年来,这两个评价指标被广泛运用于社区发现问题.
由Danon等[38]提出的NMI是用于评价所得社区划分与真实网络社区划分相似度的评价指标,给出一个网络的两种划分p1与p2,C为混淆矩阵,Cij代表p1中属于社区i的节点也属于p2中属于社区j的节点的数目总和,NMI(p1,p2)为:
NMI(p1,p2)=
其中,Cp1(Cp2)表示p1(p2)中的社区数目,Ci(Cj)表示混淆矩阵C的第i行(第j列)的元素和,N指节点总数.如果p1=p2,则NMI(p1,p2)=1,如果p1与p2完全不同,则NMI(p1,p2)=0.NMI值越大代表p1与p2的相似度越高.
由Newman等[1]提出的模块度Q是一个非常受欢迎的用来评价社区划分质量的评价函数,假设K为复杂网络中的社区划分数目,则模块度Q值定义如下:
其中,m表示网络中的边总数,lS与dS分别表示社区S中的边总数与节点总数.当Q值越接近1,表示网络的社区划分质量越好.在实际例子中,Q值一般为0.3~0.7.
2 预备知识
在E-MODTLBO/D中,由于学习规则的改变,本文中需要重新定义Chen等[13]提到的一些变量.
定义1 设Y=(y1,y2,…,yN),X=(x1,x2,…,xN),则定义函数Y=S(X)如下:
其中,j=1,2,…,N,sigmoid函数[39]定义如下:
定义2 假设Y=(y1,y2,…,yN),X=(x1,x2,…,xN),Z=(z1,z2,…,zN),则定义函数Z=XθY如下:
其中,SBestj是代表个体所有邻居中第j个节点的最多标签数.
3 改进的E-MODTLBO/D
3.1 离散化个体表示
本算法采用整数值编码规则[13],个体向量代表社区划分结果.假设一个节点的社区值与另一个节点的社区值相同,代表着两个节点属于同一社区,反之则属于不同社区.假设网络共有C个社区,N个节点,则第i个个体向量Xi定义如下:
Xi=(xi1,xi2,…,xiN),
其中,xij(1≤j≤N,1≤i≤p)代表第i个个体的第j个节点所属的社区值,p为种群大小.若xij=xik,则第i个个体的第j个节点与第k个节点属于同一社区内.除此之外,本算法采用Gong等[40]提出的一种启发式算法获得初始个体向量.
3.2 多种群进化策略
本算法采用一种改进的多种群进化策略[47].种群内所有个体以相同概率被均等地分到各个子种群内,不同子种群内部进化规则不同,以维持算法的探索能力与提高算法多样性.在每一轮迭代中,每个个体通过教学阶段与学习阶段在各个子种群内进行学习更新,子种群间进行信息交流,把种群内部表现最优的个体传给其他子种群,维持种群的多样性,避免陷入局部最优.多种群进化策略不仅可以提高算法的多样性,还可以降低时间复杂度.
3.3 自适应教学因子
在Chen等[13]提出的MODTLBO/D中,教学因子(TTF)决定平均值的改变程度与平均值对生成新解的影响程度,其值随机取为1或2,分别反映学员什么也没学到,或者是学到老师的全部知识两种情况.但在实际教学中,情况随着学习时间的推移有所不同.在教学阶段的前期,学员与教师之间的知识存在较大差距,这是由于此时学员对所学知识掌握很少,所以学员学习效率较高,学到的知识多而且快;而在教学阶段的后期,经过一段时间的学习,学员掌握的知识越来越多,与教师之间的差距越来越小,学习效率会显著下降,学到的知识少而且慢.
在优化算法中,TTF值小,则代表算法探索能力强,但搜索能力弱;反之则代表算法探索能力弱,但搜索能力强.考虑到此问题,本算法参考2015年Yue等[41]提出的自适应教学因子,改进本算法的教学因子,使得TF随着迭代次数的增加而呈线性递减,表达式如下:
其中,TTFmax与TTFmin分别表示TTF的最大值与最小值,tmax表示算法的迭代总次数,t表示当前迭代次数.从上式可以看出,在搜索前期,TTF值大;在搜索后期,TTF值小.这表明在算法搜索前期,学员学习效率高,学到的知识多且快,TTF值大有利于增强算法的全局探索能力,加快算法的收敛速度.随着迭代不断进行,学习效率下降,学到的知识少且慢,此时TTF值小有利于增强算法的局部探索能力,使算法搜索逐步向最优解靠拢,获得更高精度的解.
3.4 E-MODTLBO/D教学阶段
在实际教学中,教师给学生传播知识提高全班的知识水平,帮助学生得到较好的分数,因此全班的平均成绩也可提高,个体基于全班平均成绩与教师进行更新.本算法把每个个体分配到不同种群内,个体从种群内最优个体(STeacheri)与平均值SMeani学习更新.
STeacheri与SMeani定义如下:
STeacheri=BBest(Xi1,Xi2,…,Xik,…,XiK),
其中,Xi1,Xi2,…,Xik,…,XiK代表个体Xi所在种群的个体集合,且Xik=(xik1,xik2,…,xikD).
在教学阶段,教师的任务是提高全班的成绩,通过对最优个体的学习来提高整体水平,因此,对社区发现问题重新定义对第i个个体Xi的更新规则:
newXi=Xiθ Differencei,
Differencei=S(rand(0,1)×(STeacheri⨁
(TTF(t)×SMeani))),
其中,rand(0,1)是0与1之间的随机数,TTF(t)是前文3.3节提到的自适应教学因子,(STeacheri)与SMeani分别是个体Xi所在种群的最优个体与平均值,⨁是异或算子.
3.5 E-MODTLBO/D学习阶段
在学习阶段,学生随机向种群内的其他学生学习知识,学生从其他学生那里学习他们还未掌握的新知识.在这一阶段,个体通过以下规则更新:
newXi=Xiθ Differencei,
Differencei=S(Xi⨁Xj),
其中,⨁是异或算子,Xj代表Xi所在种群内部的任意个体,这种策略被称为随机学习策略.
为了提高算法的表现效果,本算法提出一种改进的量子行为学习策略[42].在学习阶段,每个个体在各自的子种群内可以采用随机学习策略或者是改进的量子行为学习策略.给出学习概率pl,决定个体在学习阶段采用的学习策略.随机产生一个介于0与1之间的随机数r,当r 假设产生的新个体newXi=(z1,z2,…,zN),改进的量子行为学习策略规则如下: zj= 其中,STeacher与GTeacher分别表示个体Xi所在种群内的最优个体与全局最优个体,且TempX定义如下: TempX=β×(X⨁SMeani)×(-log(u)), 其中,u为介于0与1之间的随机值,SMeanj是个体Xj所在种群内的平均值.在传统的学习阶段,个体只是在种群中随机选择个体进行学习,而本算法中,个体有两种不同的学习策略.在一定概率下,个体采用传统的随机学习策略;但在一定概率下,个体通过向全局最优个体与种群内最优个体学习知识,使得个体可以在其他个体、全局最优个体与种群内最优个体的共同帮助下学习,使学习效率明显提高,加快算法收敛速度. 当算法中存在完全相同的两个解,则必须修改它们以避免陷入局部最优,维持种群多样性.采用Gong等[40]提出的基于邻居的变异算子,对每个个体随机生成一个介于0与1之间的数,如果小于变异概率pm,则执行变异算子.这里需要指出每次教学阶段或者学习阶段完成后,都需进行一次变异操作. 3.7.1 基于分解的多目标优化算法(MOEA/D) MOEA/D[43]是基于传统的多目标最优化策略的算法,该算法把多目标优化问题分解为一系列单目标子问题,同时最优化这些子问题,每个子问题通过其邻居子问题进行优化,而子问题的邻居关系通过子问题之间的距离与聚合多目标权重向量定义.不同于传统的帕累托分级方法,该算法通过实现每个子问题的最优化来获得最优解. 在MOEA/D中,有许多方法可以把多目标最优化算法分解为一系列子问题,其中一种是通过构造聚合函数实现分解.至今为止,有许多方法可以构造聚合函数,其中最受欢迎的是权重求和法与切比雪夫法.本算法采用切比雪夫法,因为所研究的问题中两个目标函数是不连续的,所以不能简单判断铂累托前沿(PF)是不是凹的.如果PF是凸的,权重求和法的效果就会不佳.切比雪夫法把问题分割为一些具有单目标子问题[43],最优化问题可以表示为 3.7.2 目标函数 采用Gong等[30]提出的两个目标函数NRA与RC,目标是最小化这两个函数.定义一个无向图G=(V,E),定义邻接矩阵A,一种划分方法S=(V1,V2,…,Vm),Vi是社区Gi的节点集合,i=1,2,…,m.定义L(V1,V2)=∑i∈V1,j∈V2Aij,L(V1,V2)=∑i∈V1,j∉V2Aij.目标函数如下: 一般而言,NRA可看作是社区内部连接的密度,RC可看作是社区之间连接的密度.最小化NRA趋向于把网络切割成很多的小型社区,而最小化RC趋向于把网络切割成大型社区,这两个目标函数有着权衡对方对于社区数目增加或者减少的趋势的潜力.通过权衡最小化这两个目标函数,可以获得高质量的网络划分. 3.7.3E-MODTLBO/D伪代码 本文中采用MOEA/D的主要框架,加入多种群进化策略,在每个种群内部,个体通过种群内部信息进行更新进化.因此,NTeacheri与NMeani代表第i个个体所在种群内部最优值与平均值.E-MODTLBO/D的伪代码如下: 算法:E-MODTLBO/D 输入:初始化个体X,个体数目N,迭代次数genmax,变异概率pm,学习概率pl,种群数目Sp,种群内个体数目SN,权重向量W,初始化最优参考点z*; 输出:最优个体 Begin fort=1:genmax 把个体X随机分入不同种群内,更新全局最优个体与种群内最优个体; for每个种群 do 通过教学阶段与学习阶段更新每个个体Xi,计算个体与全局最优参考点的距离z*; 保留每个种群内表现最优的SN个个体; 更新全局最优参考点z*; end for 把种群内最优个体传给其他种群,并保留前SN个个体在种群内; end for End 所有实验都在2.3 GHz CPU,4 GB RAM的处理器上运行,操作系统为Windows7,软件版本为MATLAB 8.3.为了减少系统误差,每个函数都被单独运行了20次.对于所有的方法,种群大小popsize设置为100,更新迭代次数ggenmax设置为100,变异概率pm=0.06,种群数目设置为20,种群内个体数目为5.为了维持算法多样性与收敛性的平衡,设置学习概率pl=0.5. 采用Zachary空手道俱乐部网络、Bottlenose海豚网络、美国大学足球队网络和Krebs美国政治书网络这4个真实的复杂网络对本算法进行验证. 空手道俱乐部网络由Zachary提出[44],通过观察在一段时期内空手道俱乐部34名成员的活动所获得.在研究期间,俱乐部管理者与俱乐部开发者之间存在分歧,这个分歧最终导致开发者离开并且成立新的俱乐部;与此同时,开发者带走原俱乐部近1/2成员,网络自然分成了两个大小相近的社区. Bottlenose海豚网络由62只海豚构成[45],海豚们住在新西兰的一个神奇峡湾中,它们的行为活动被Lusseau等学者所观察.学者们花了7年时间观察它们的行为活动,定义如果有两只海豚发生固定且频繁的协作行为,则认为这两只海豚之间有联系.这个网络中的海豚自然的分成2组,共有159组联系. 美国大学足球队网络来自于对美国大学足球队的观察[20],网络代表在Fall 2000常规赛赛季中不同球队之间的比赛场次,网络中的节点代表足球队,而边则代表两个足球队会进行比赛.比赛队伍会被分到几个不同的联盟中去,每队平均进行4场联盟间比赛与7场联盟内比赛,该网络包含115个节点与616条边. Krebs的政治书网络中,节点代表105本购自亚马逊的关于美国政治的书,边代表经常由同一个买家买的书之间具有关联关系.不同的书按不同的政治取向被分类[46]. 为了评价本算法在复杂网络的社区发现问题中的表现,把本算法与其他一些经典的算法进行比较. 首先,与两个经典的单目标算法:FM算法[21](采用贪心策略实现模块度Q最优),BGLL算法进行比较,结果如表1所示. 表1 4个真实网络的模块度Q值Tab.1 The modularity values obtained on four real-world networks 从表1可以看出:在Zachary空手道俱乐部网络中,BGLL算法表现最优,可以获得最大的模块度Q值为0.421 08;而对于另外3个网络,E-MODTLBO/D算法表现最优,比其他两个单目标算法表现都要好. 其次,把E-MODTLBO/D与一些多目标进化算法进行比较,分别为MOCD[28]、MOGA-Net[29]、MOEA/D-Net[30]、MODPSO[31]和MODTLBO/D[13],所得结果如表2所示. 表2 4个真实网络的模块度Q值与标准互换信息NMI Tab.2 Results obtained on four real-world networks 算法QNMIZachary空手道俱乐部Battlenose海豚美国大学足球队Krebs美国政治书Zachary空手道俱乐部Battlenose海豚美国大学足球队Krebs美国政治书MOCD0.418760.521950.595860.525740.837181.000000.893320.59498MOGA-Net0.414940.514170.526480.517420.837181.000000.801160.59419MOEA/D-Net0.419790.521180.603980.526551.000001.000000.926790.59642MODPSO0.419790.526050.604550.526621.000001.000000.928850.61583MODTLBO/D0.419790.522010.604550.526721.000001.000000.926680.61727E-MODTLBO/D0.419790.526800.604570.526941.000001.000000.924200.67710 从表2可以看出:从模块度Q值的角度比较,在Zachary空手道俱乐部网络中,E-MODTLBO/D与MOEA/D-Net、MODPSO、MODTLBO/D表现同样好;但在另外3个网路中,E-MODTLBO/D比其他算法表现更优.从NMI这个评价指标来看,在Zachary空手道俱乐部网络中,E-MODTLBO/D与MOEA/D-Net、MODPSO、MODTLBO/D表现同样好;在Battlenose海豚网络中,所有算法的NMI值都可以达到1;在美国大学足球队网络中,MODPSO表现最优,NMI值为0.928 85,本算法的NMI值为0.924 20.在Krebs美国政治书网络中,本算法表现最优,可以获得最大的NMI值,为0.677 10,远大于其他算法. 从与这些算法比较中更可以看出,本算法在解决社区发现问题时是很有潜力的.在NMI值上来看,它可以在Zachary空手道俱乐部网络、Bottlenose海豚网络与Krebs美国政治书网络中都表现优于其他算法;从Q值来看,它在4个网络中的表现都优于其他算法. 本文中提出了一种高效的在多种群进化策略下的E-MODTLBO/D.不同于MODTLBO/D,本算法采用多种群进化策略来降低时间复杂度并且增加算法的多样性.种群内所有个体以相同概率被均等地分到各个子种群内,不同子种群内部进化规则不同,以维持算法的探索能力.每个个体在教学阶段与学习阶段在各个种群内进行学习更新,每次迭代后,种群间进行信息交流,把种群内部表现最优的个体传给其他种群,以维持种群的多样性,避免陷入局部最优.在教学阶段,每个个体从种群内学习,同时采用自适应教学因子.在学习阶段,每个个体在各自的子种群内采用随机学习策略或者是改进的量子行为学习策略,以保证算法的收敛性与多样性.在每代更新完成后,子种群之间的信息交流可以维持算法的多样性与避免早熟收敛. 为了验证提出该算法的有效性,把该算法运用于不同的真实网络中,并与其他算法进行比较.实验结果表明,该算法在时间复杂度与发现高质量的社区结构方面要优于MODTLBO/D等一些经典社区发现算法,在解决复杂网络中的社区发现问题方面高效且有广泛应用前景. 为了让该算法更加高效,未来的工作将致力于研究基于特殊问题的更新策略与如何维持多样性与收敛性的方法.进而将离散性基于教与学最优化的方法运用于限制性的、动态的复杂网络中,这有助于解决各种各样的真实复杂网络的最优化问题. [1] NEWMAN M E J,GIRVAN M M.Finding and evaluating community structure in networks[J].Phys Rev E,2004,69(2):99-106. [2] NEWMAN M E J.Fast algorithm for detecting community structure in networks[J].Phys Rev E,2004,69(6):066133. [3] RAO R V,SAVSANI V J,VAKHARIA D P.Teaching-learning-based optimization:an optimization method for continuous non-linear large scale problems[J].Information Sciences,2012,183(1):1-15. [4] YU K,WANG X,WANG Z.Constrained optimization based on improved teaching-learning-based optimization algorithm[J].Information Sciences,2016,352/353:61-78. [5] GHASEMI M,GHAVIDEL S,GITIZADEH M,et al.An improved teaching-learning-based optimization algorithm using Levy mutation strategy for non-smooth strategy for non-smooth power flow[J].International Journal of Electrical Power& Energy Systems,2015,65:375-384. [6] BASU M.Teaching-learning-based optimization algorithm for multi-area economic dispatch[J].Energy,2014,68:21-28. [7] PATEL V K,SAVSANI V J.A multi-objective improved teaching-learning-based optimization algorithm (MO-ITLBO) [J].Information Sciences,2014,357:182-200. [8] KEESARI H S,RAO R V.Optimization of job shop scheduling problems using teaching-learning-based optimization algorithm[J].Opsearch,2013,51(4):545-561. [9] XIA K,GAO L,LI W D,et al.Disassembly sequence planning using a simplified teaching-learning-based optimization algorithm[J].Advanced Engineering Informatics,2014,28:518-527. [10] BAYKASOGLU A,HAMZADAYI A,KOSE S Y.Testing the performance of teaching-learning-based optimization (TLBO) algorithm on combinatorial problems:Flow shop and job shop scheduling cases[J].Information Sciences,2014,276(C):204-218. [11] DEDE T.Application of teaching-learning-based-optimization algorithm for the discrete optimization of truss structures[J].Ksce Journal of Civil Engineering,2014,18(6):1759-1767. [12] LI J,PAN Q,MAO K.A discrete teaching-learning-based optimization algorithm for realistic flow shop rescheduling problems[J].Engineering Applications of Artificial Intelligence,2015,37:279-292. [13] CHEN D,ZOU F,LU R Q,et al.Multi-objective optimization of community detection using discrete teaching-learning-based optimization & with decomposition[J].Information Sciences,2016,369:402-418. [14] EZHILARASI G A,SWARUP K S.Network decomposition using Kernighan-Lin strategy aided harmony search algorithm[J].Swarm & Evolutionary Computation,2012(7):1-6. [15] POTHEN A,SIMON H,LIOU K P.Partitioning sparse matrices with eigenvectors of graphs[J].Siam Journal on Matrix Analysis & Applications,1990,11(3):430-452. [16] FIEDLER M.A property of eigenvectors of non-negative symmetric matrices and its applications to graph theory[J].Czechoslovak Mathematical Journal,1975,25:619-637. [17] WEI Y C,CHENG C K.Ration cut partitioning for hie-rarchical designs[J].IEEE Transactions on Computer-Aided Design,1991,10(7):911-921. [18] HE L,ZHANG H.Iterative ensemble normalized cuts[J].Pattern Recognition,2015,52:274-286. [19] ZHANG X,FEI S,SONG C,et al.Label propagation algorithm based on local cycles for community detection[J].International Journal of Modern Physics B,2015,29(5):1550029. [20] GIRVAN M,NEWMAN M E J.Community structure in social and biological networks[J].Proceedings of the National Academy of Sciences of the United States of America,2002,99(12):7821-7826. [21] CLAUSET A,NEWMAN M E J,MOORE C.Finding community structure in very large networks[J].Physical Review E,2004,70(2):066111. [22] BLONDEL V D,GUILAUME J L,LAMBIOTTE R,et al.Fast unfolding of communities in large networks[J].Journal of Statistical Mechanics:Theory and Experiment,2008,10:P10008. [23] CRUZ J D,BOTHOREL C,POULET F.Entropy based community detection in augmented social networks[C]∥International Conference on Computational aspects of Social Networks.Salamanca:IEEE,2011:163-168. [24] HASSAN E A,HAFEZ A I,HASSANIEN A E,et al.Community detection algorithm based on artificial fish swarm optimization[J].Advances in Intelligent Systems & Computing,2014,323:509-521. [25] KARIMI-MAID A M,FATHIAN M,AMIRI B.A hybrid artificial immune network for detecting communities in complex networks[J].Computing,2015,97(5):483-507. [26] LI Y,LIU J,LIU C.A comparative analysis of evolutio-nary and memetic algorithms for community detection from signed social networks[J].Soft Computing,2014,18(2):329-348. [27] LI Z,LIU J.A multi-agent genetic algorithm for community detection in complex networks[J].Physica A Statistical Mechanics & Its Applications,2016,449:336-347. [28] SHI C,YAN Z,CAI Y,et al.Multi-objective community detection in complex networks[J].Applied Soft Computing,2012,12(2):850-859. [29] PIZZUTI C.A multi-objective genetic algorithm to find communities in complex networks[J].IEEE Transactions on Evolutionary Computation,2012,6(3):418-430. [30] GONG M G,MA L,ZHANG Q F,et al.Community detection in networks by using multi-objective evolutionary algorithm with decomposition[J].Physica A Statistical Mechanics & Its Application,2012,391:4050-4060. [31] GONG M G,CAI Q,CHEN X,et al.Complex network clustering by multi-objective discrete particle swarm optimization based on decomposition[J].IEEE Transactions on Evolutionary Computation,2014,18(1):82-97. [32] AMIRI B,HOSSAIN L,CRAWFORD J W,et al.Community detection in complex networks:multi-objective enhanced firefly algorithm[J].Knowledge-Based Systems,2013,46:1-11. [33] CAI Q,GONG M G,MA L,et al.Greedy discrete particle swarm optimization for large-scale social network clustering[J].Information Sciences,2015,316(41):503-516. [34] LIU C,LIU J,JIANG Z.A multi-objective evolutionary algorithm based on similarity for community detection from signed social networks[J].IEEE Transactions on Cybernetics,2014,44(12):2274-2287. [35] ZHAO Y,LI S,JIN F.Overlapping community detection in complex networks using multi-objective evolutionary algorithm[J].Computational & Applied Mathematics,2015,36(1):1-20. [36] ZHOU X,LIU Y,LI B,et al.Multi-objective biogeography based optimization algorithm with decomposition for community detection in dynamic networks[J].Physica A:Statistical Mechanics & Its Applications,2015,436:430-442. [37] RADICCHI F,CASTELLANO,CECCONI F,et al.Defining and identifying communities in networks[J].Proceedings of the National Academy of Sciences of the United States of America,2004,101(9):2658-2663. [38] DANON L,DAZ-GUILERA A,DUCH J,et al.Comparing community structure identification[J].Journal of Statistical Mechanics Theory & Experiment,2005,78:P09008. [39] KENNEDY J,EBERHART R C.A discrete binary version of the particle swarm algorithm[J].Computational Cybernetics and Simulation,1997,5:4104-4108. [40] GONG M G,CAI Q,LI Y,et al.An improved memetic algorithm for community detection in complex networks[C]∥2012 IEEE Congress on Evolutionary Computation.Brisbane:IEEE,2012:1-8. [41] YUE Z,GAO Y.An improved teaching-learning-based optimization algorithm[J].Journal of Lanzhou University of Technology,2015,41(6):99-103. [42] ZOU F,WANG L,HEI X,et al.Teaching-learning-based optimization with dynamic group strategy for global optimization[J].Information Sciences,2014,273:112-131. [43] ZHANG Q F,LI H.MOEA/D:a multi-objective evolutionary algorithm based on decomposition[J].IEEE Transactions on Evolutionary Compution,2017,11(6):712-731. [44] ZACHARY W W.An information flow model for conflict and fission in small groups[J].Journal of Anthropological Research,1997,33(4):452-473. [45] LUSSEAU D,SCHNEIDER K,BOISSEAU O J,et al.The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations[J].Behavioral Ecology and Sociobiology,2003,54(4):396-405. [46] NEWMAN M E J.Modularity and community structure in networks[J].Proceedings of the National Academy of Science,2006,103 (23):8577-8582. [47] ROSINC C,BELEW R,MORRIS G,et al.New methods for competitive co-evolution[J].Evolutionary Computation,1997,5(1):1-29.3.6 变异规则
3.7 算法框架
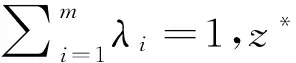
4 实验结果
4.1 参数设置
4.2 真实网络
4.3 实验结果分析
5 结 论

