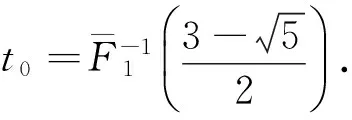具有广义Gumbel分布的两部件系统故障率的某些性质
蔡南莲,陈 豪
(集美大学理学院,福建厦门361021)
1 预备知识
先介绍几个概念:


(ii)称随机变量X是IFR(increasing failure rate),如果X的故障率λ(t)关于t单调不降.
故障率的概率解释:当Δt很小时,λ(t)表示部件在t之前正常工作条件下,在[t,t+Δt]中失效的概率.
接下来介绍下面的二维联合分布函数.
设F1(x),F2(x),x>0为非负随机变量的分布函数,可以构造如下二维联合分布函数
F(x1,x2)=F1(x1)F2(x2)[1+α(1-F1(x1))
(1-F2(x2))],x1,x2>0,-1≤α≤1.
(1)
对应的联合生存函数为
F2(x2)],x1,x2>0,-1≤α≤1.
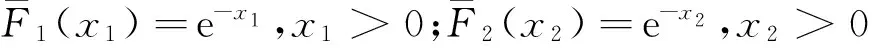
F(x1,x2)=(1-e-x1)(1-e-x2)
[1+αe-x1-x2],x1,x2>0.
(2)
(1-e-x2)],x1,x2>0.
定义2 (i) 如果(X1,X2)的联合分布函数为式(2),称(X1,X2)服从二维标准Ⅱ型Gumbel指数分布;
(ii) 如果(X1,X2)的联合分布函数为式(1),称(X1,X2)服从广义的二维Gumbel分布,该分布也称为FGM copula(Farlie-Gumbel-Morgenstern copula)分布[3]函数.
二维标准Ⅱ型Gumbel指数分布由Gumbel提出[4],显然它是广义的二维Gumbel分布(即FGM copula分布)的特殊情形.
容易得出,设随机向量(X1,X2)服从广义的二维Gumbel分布(2),则当α=0时,(X1,X2)是相互独立的;当α≠0时,(X1,X2)是不相互独立的.
近年来,FGM copula分布在风险模型、应用统计中的应用研究引起了国内外很多学者的关注.如Tahmasebi等[5]研究了样本具有FGM copula分布时相伴次序统计量相关的性质;Yan等[6]研究了FGM copula分布的某些老化性质;Jiang等[7]探讨了风险模型中,理赔量和理赔时间服从FGM copula分布时破产前最大盈余的分布.
故障率和次序统计量是可靠性理论中的重要概念.最大、最小次序统计量分别对应着并联、串联系统寿命.近年来,有关故障率和次序统计量的研究引起了国内外学者的广泛关注,很多学者在独立假设下研究次序统计量.如Boland等[8]探讨了相互独立的不同分布的样本次序统计量在故障率次序下的随机比较性质,并得到了两个独立具有指数分布的部件并联系统的故障率的上界;Khaledi等[9]研究了多个相互独立的具有不同的指数分布的部件的并联系统故障率的性质,并得到了多个不同的指数分布部件并联系统故障率的上界,该上界优于Boland等[8]得到的;更多的文献可参见Balakrishnan等[10]的文章,该文综述了近年来在样本独立情形下有关次序统计量的随机比较性质的研究.
Joo等[11]在相依假设下,研究了两个部件的并联、串联系统的故障率性质.他们假设部件寿命的联合分布服从二维标准Ⅱ型Gumbel指数分布(2)时,得出了并联系统和串联系统寿命的故障率的一些性质.
本文中进一步讨论了两个同边际分布的部件,其联合分布函数为广义的二维Gumbel分布(1)时,并联系统和串联系统寿命的故障率性质,推广了文献[11]中的某些结论,得到某些更一般的结果.
本文中均假设随机变量非负,分布函数是绝对连续的,具有概率密度函数;文中提到“单调增加”均指“单调不降”,“单调下降”均指“单调不增”.
2 串联系统的故障率性质
假设(X1,X2)的联合分布函数为式(1),X1,X2有相同的分布函数为F1(x)及故障率函数λ1(t).以X1,X2为部件的串联系统寿命记为X(1)=min(X1,X2),则可求得X(1)的生存函数为
求导得密度函数为
[1+αF1(t)(-1+2F1(t))],t>0.
所以X(1)的故障率函数为
(3)
上式恒等变形得
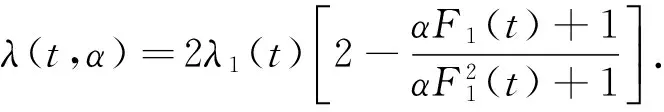
(4)
先介绍下面的引理.

(i) -1≤α<0 时,当0
(ii) 0<α≤1 时,当0

(u-u1)(u-u0).
(i) -1≤α<0时,u1>1,u-u1<0.当0
下面讨论串联系统寿命X(1)的故障率的性质,其中的定理都采用上面的记号.
定理1 串联系统寿命X(1)的故障率λ(t,α)满足:
(i) 0<α≤1时,λ(t,α)≤2λ1(t);
(ii) -1≤α<0时,2λ1(t)≤λ(t,α)≤4λ1(t);
(iii)α=0时,λ(t,α)=2λ1(t).
证明 (i) 0<α≤1时,
代入式(4),(i)得证.
(ii) -1≤α<0时,
代入式(4),(ii)得证.
(iii)α=0代入式(4)即得.
定理2 串联系统寿命X(1)的故障率λ(t,α)有如下性质:
(i)λ(t,α)关于α单调下降,α∈[-1,1];
(ii)α=-1时,设X1是IFR,则X(1)也是IFR.
证明 (i) 由式(4)得
(i)得证.
(ii)α=-1时,由式(4)得:
题设X1是IFR,即λ1(t)关于t单调增加,从而λ(t,α)关于t单调增加,(ii)得证.
注1 当部件寿命X1表示均值为1的指数分布时,定理2的结论就是文献[11]中定理3.4和定理3.3(i).
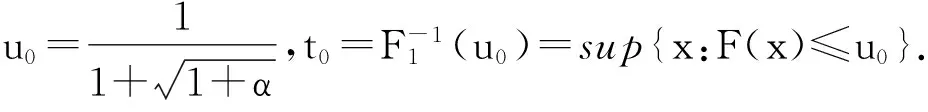
(i) -1≤α<0,设λ1(t)满足0
(ii) 0<α≤1,设λ1(t)满足0
(iii)α=-1,设X1是IFR,则X(1)也是IFR.

λ(t,α)=2λ1(t)[2-H(F1(t))].
(5)
(i) -1≤α<0,u0=F1(t0).
当0 当t>t0时,u=F1(t)>u0,由引理1(i),H(u)关于u单调增加,因u=F1(t)关于t单调增加,故H(F1(t))关于t单调增加,题设λ1(t)为常数,由式(5)得:λ(t,α)关于t单调下降. (ii) 证明方法同(i),略去. 下面的两个例子说明,存在满足定理3的条件的分布. 例1 设随机变量X的生存函数为 X的故障率 λ(t)关于t∈[0,0.5]单调增加,当t>0.5为常数. 例2 设随机变量X的生存函数为 X的故障率 当t∈[0,1]时,λ(t)为常数,t>1时单调增加. 由定理3容易得如下的推论. (i) -1≤α<0,0 (ii) 0<α≤1,0 (iii) α=-1,X(1)是IFR. 注2 推论1即为文献[11]中定理3.3(ii). 假设(X1,X2)的联合分布函数为式(1),X1,X2有相同的分布函数F1(x),密度函数f(t),故障率函数λ1(t).以X1,X2为部件的并联系统寿命为X(2)=max(X1,X2).求得X(2)的生存函数为 即 求导得密度函数 从而X(2)的故障率函数为 化简得: h(t,α)=2λ1(t) (6) 令 0≤u≤1. 则 (7) 下面讨论并联系统寿命X(2)的故障率h(t,α)的性质,以下定理都采用上面的记号. 定理4 并联系统寿命X(2)的故障率h(t,α)≤4λ1(t). 证明 由式(7),只要证明:0≤u<1时,K(u,α)>0即可. -1≤α≤1时,K(u,α)的分子为: 3-(1+α)u+αu2=2+(1-u)(1-αu)≥2. (i) 当0≤α≤1时,K(u,α)的分母为: 2-(1+α)u+2αu2-αu3≥2-(1+α)u+ αu2=1+(u-1)(αu-1)≥1; (ii) 当-1≤α<0时,K(u,α)的分母为: 2-(1+α)u+2αu2-αu3=(u-1)(αu-1)+ (1+αu2)+(-αu3)>0. 证明 计算得 -u(u-1)(u2-3u+1)= 推论2 (X1,X2)的联合生存函数为式(2),-1≤α1<α2≤1.则并联系统寿命X(2)的故障率h(t,α)有如下性质:当0 注3 推论2就是文献[11]中定理3.6. 引理2 令0≤u<1, A(u,α)=(2-(1+α)u+2αu2-αu3)2 则 (i)A(u,α)=(1+α)+8αu(u-1)+u2(1-u)[2α+α2(1-u)]; (ii)A(u,α)=(1+α)+6αu(u-1)-2αu(1-u)2+α2u2(1-u)2. 证明 计算得A(u,α)=1+α-8αu+(10α+α2)u2-(2α+2α2)u3+α2u4,则(i)、(ii)易得. 定理6 对任意-1≤α≤1,设X1是IFR,则并联系统寿命X(2)也是IFR. (1+α)+8αu(u-1)+u2(1-u)[2α+ α2(1-u)]≥(1+α)-2α+0=1-α≥0. (ii) -1≤α<0,由引理2(ii)得 A(u,α)=(1+α)+6αu(u-1)- 2αu(1-u)2+α2u2(1-u)2≥0. 由于指数分布的故障率为常数,由定理6可以得出如下的推论. 推论3 设(X1,X2)的联合分布函数为(2),则对任意-1≤α≤1,并联系统寿命X(2)是IFR. 注4 推论3即为文献[11]中定理3.5. [1] MULLER A,STOYAN D.Comparison methods for stochastic models and risks[M].New York:John Wiley & Sons,2002:10. [2] 曹晋华,程侃.可靠性数学引论[M].北京:高教出版社,2006:8. [3] NELSEN R B.An introduction to copulas[M].New York:Springer-Verlag,1999:68. [4] GUMBEL E J.Bivariate exponential distributions[J].J Amer Statist Assoc,1960,55:698-707. [5] TAHMASEBI S,BEHBOODIAN J.Information properties for concomitants of order statistics in Farlie-Gumbel-Morgenstern (FGM) family[J].Communications in Statistics-Theory and Methods,2012,41(11):1954-1968. [6] YAN R,YOU Y,LI X.On bivariate ageing propertied of exchangeable Farlie-Gumbel-Morgenstern distributions[J].Communications in Statistics-Theory and Methods,2017,46(23):11843-11853. [7] JIANG W,YANG Z.The maximum surplus before ruin for dependent risk models through Farlie-Gumbel-Morgenstern copula[J].Scandinavian Actuarial Journal,2016(5):385-397. [8] BOLAND P J,EL-NEWEIHI E,PROSCHAN F.Applications of the hazard rate ordering in reliability and order statistics[J].Journal of Applied Probability,1994,31:180-192. [9] KHALEDI B E,KOCHAR S.Some new results on stochastic comparisons of parallel systems[J].Journal of Applied Probability,2000,37:1123-1128. [10] BALAKRISHNAN N,ZHAO P.Ordering properties of order statistics from heterogeneous populations:a review with an emphasis on some recent developments[J].Probability in the Engineering and Informational Science,2013,27:403-443. [11] JOO S,MI J.Some properties of hazard rate functions of systems with two components[J].Journal of Statistical Planning and Inference,2010,140:444-453.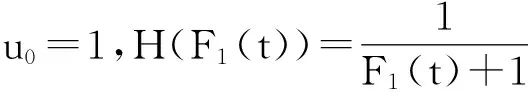
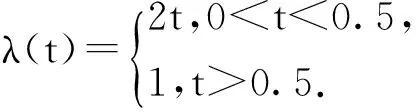
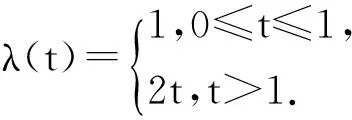

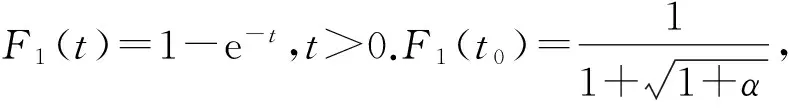
3 并联系统的故障率性质