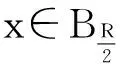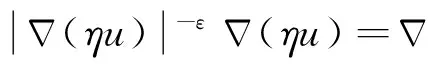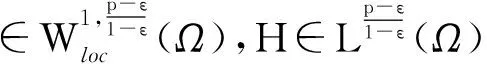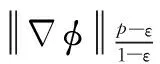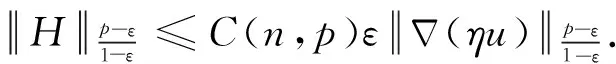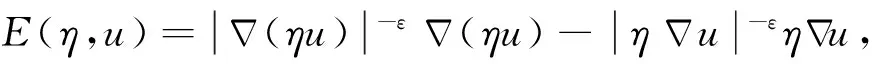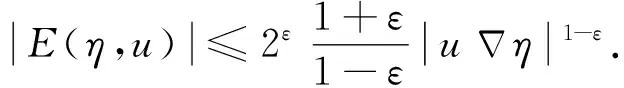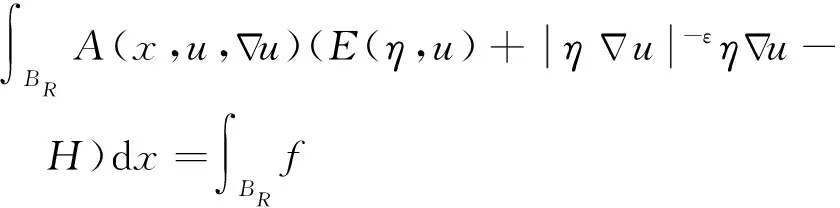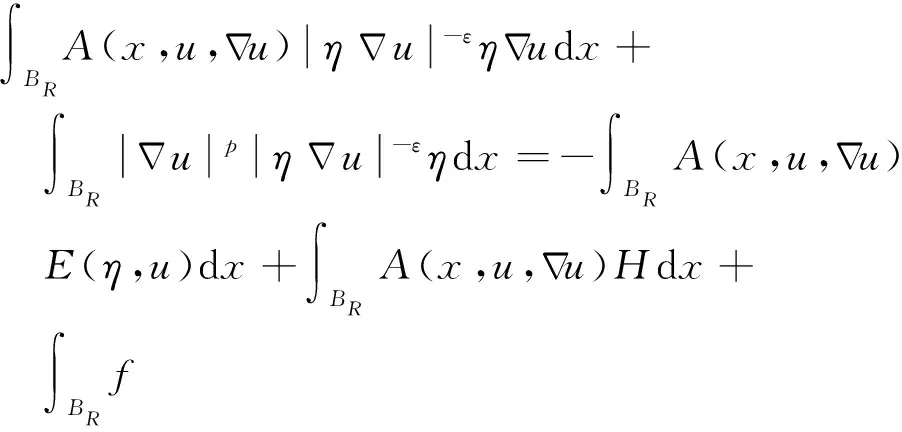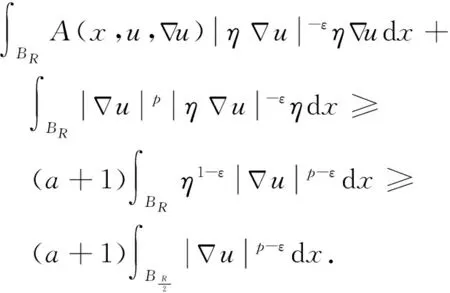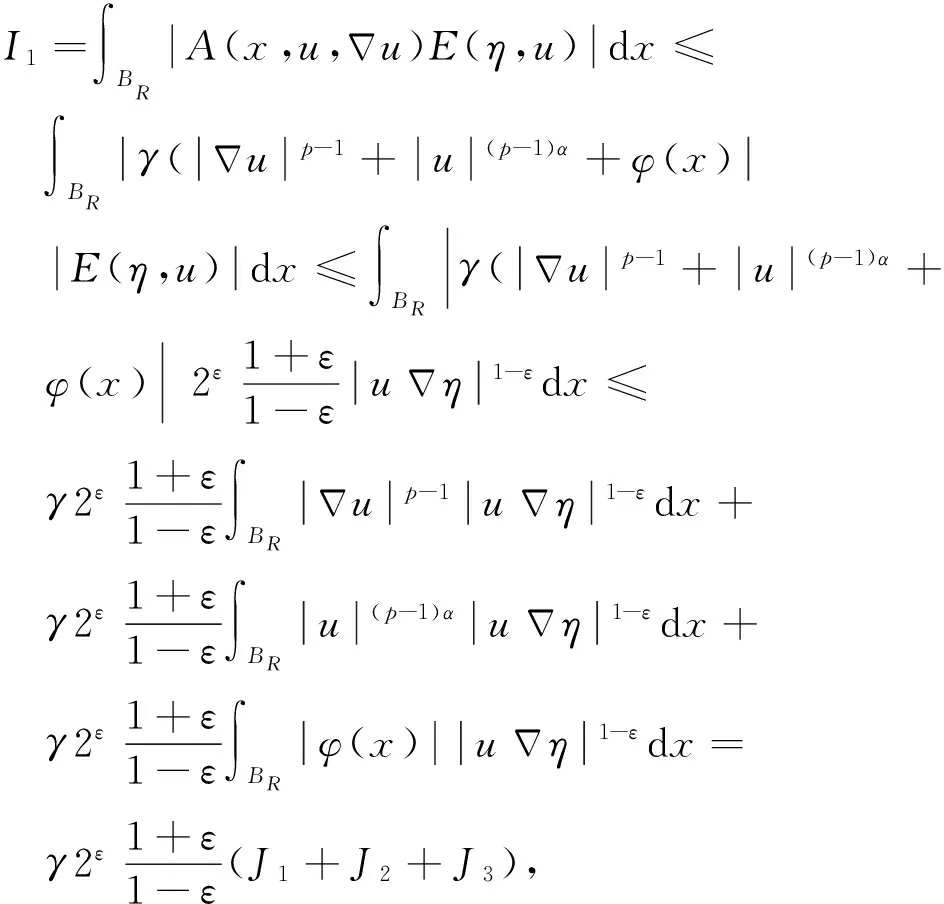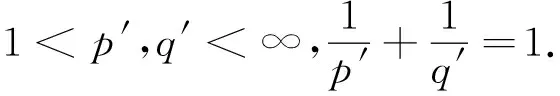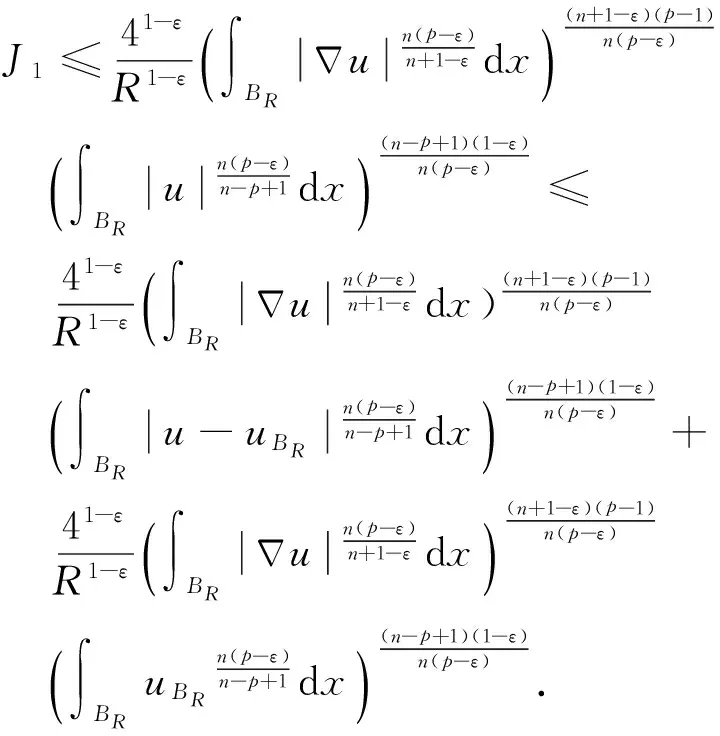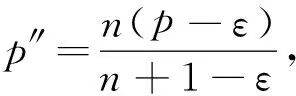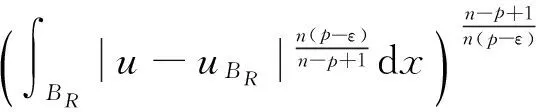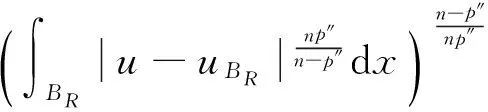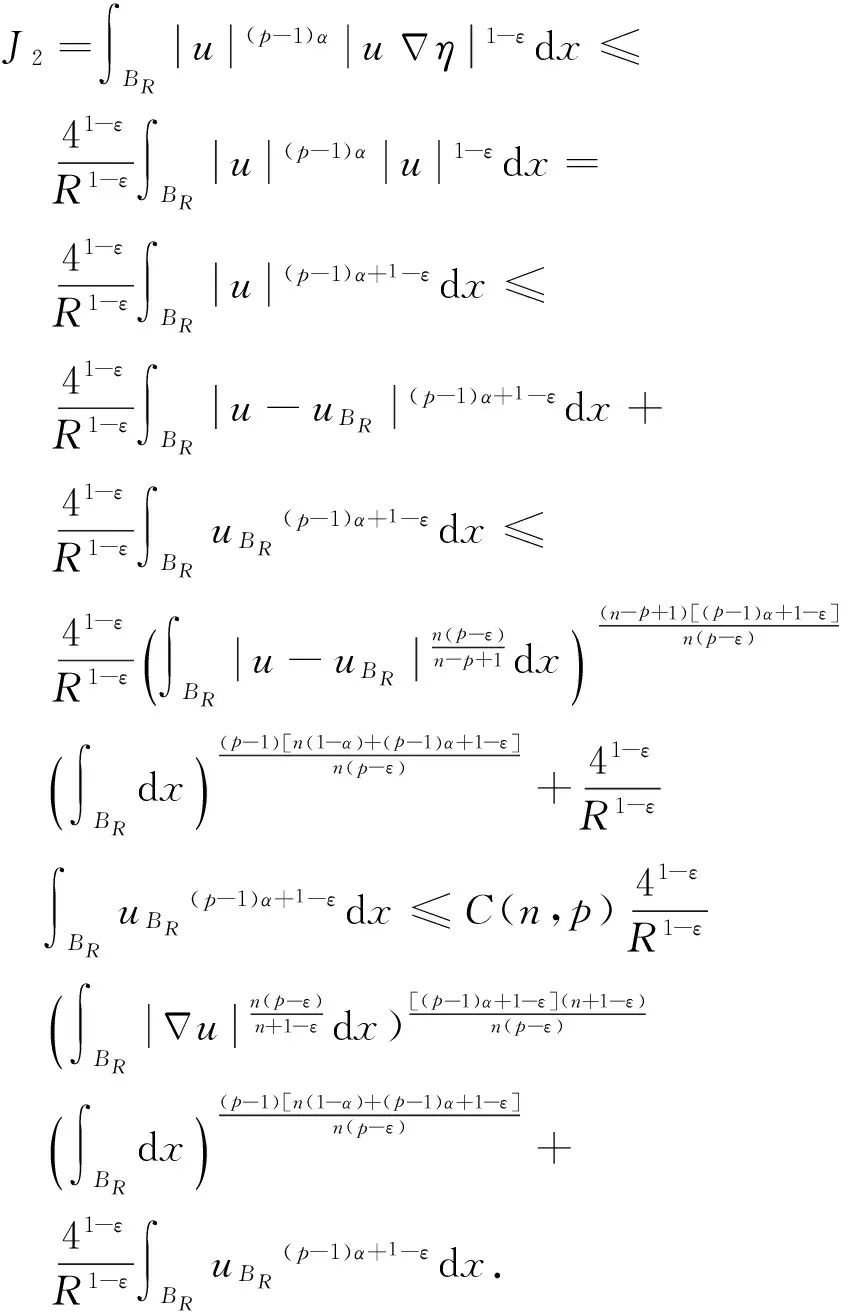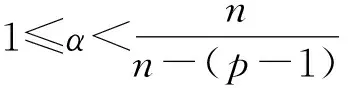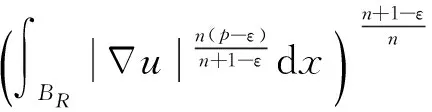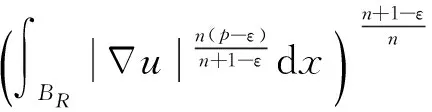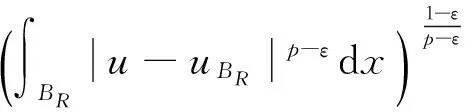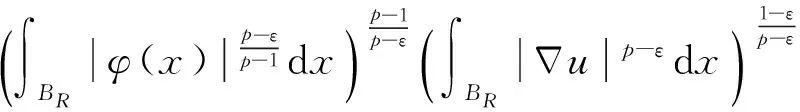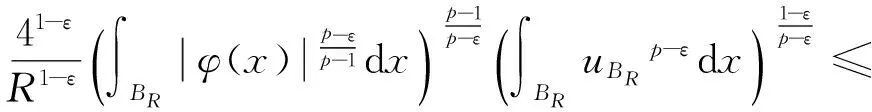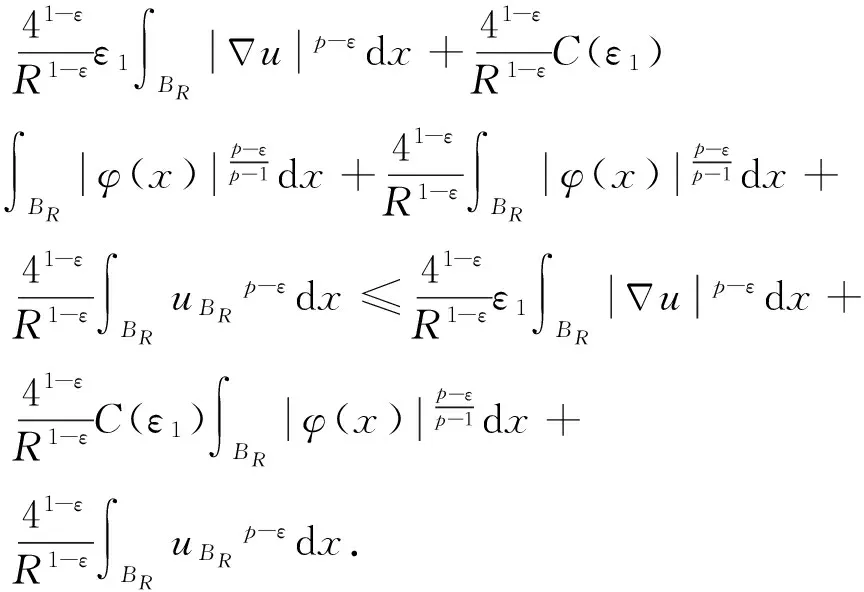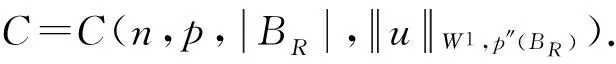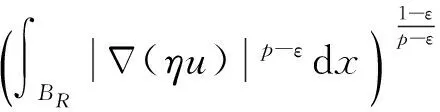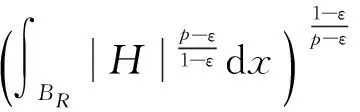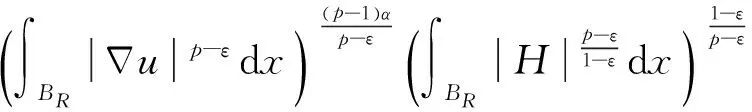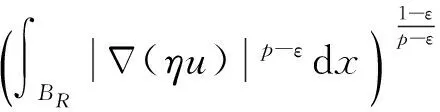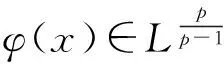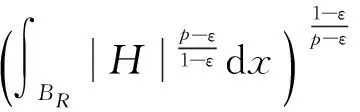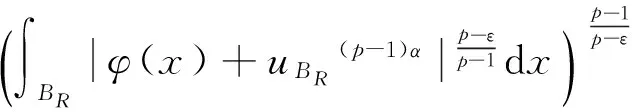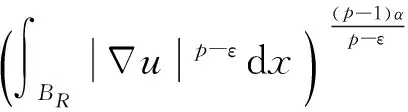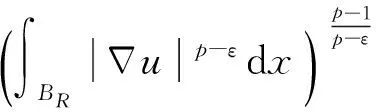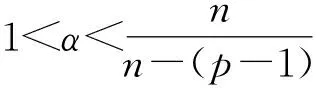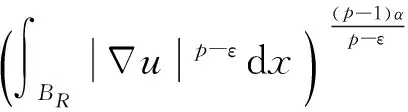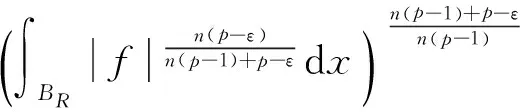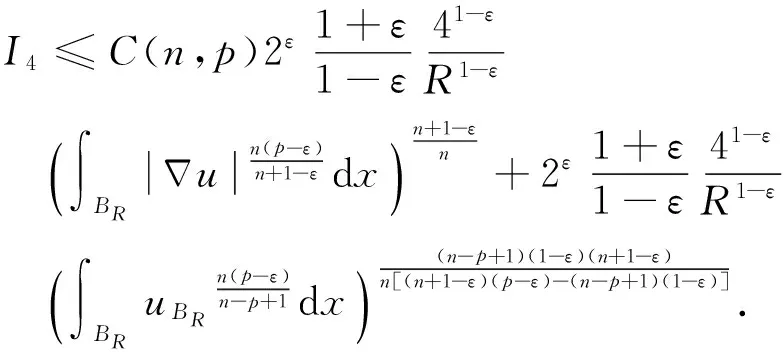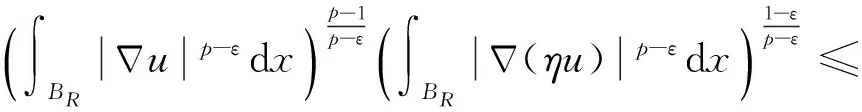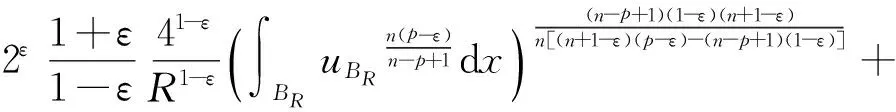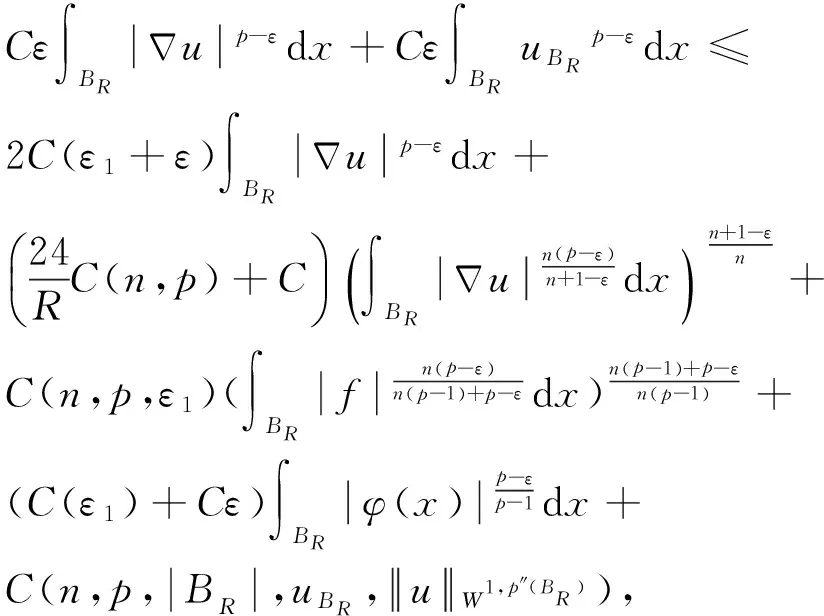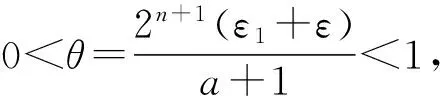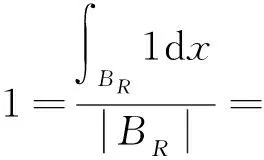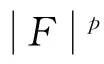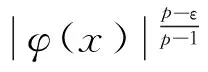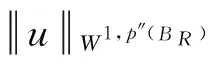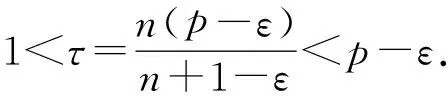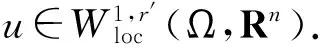非齐次拟线性A-调和方程很弱解的正则性
朱坤杰,陈淑红
(闽南师范大学数学与统计学院,福建漳州363000)
1 预备知识
本文中主要考虑非齐次拟线性A-调和方程
(1)
很弱解的正则性.其中Ω⊂Rn是有界区域,n≥2,1 (i) 算子A(x,u,h)满足强制性条件.即存在常数a>0,使得 u∈Rn; (ii) 算子A(x,u,h)是拟线性的.即存在常数β>0,使得 (A(x,u1,h1)-A(x,u2,h2))(h1-h2)≥ ∀u1,u2∈Rn,h1,h2∈RnN,x∈Ω; (iii) 算子A(x,u,h)是有界的.即存在常数β≤γ<∞,使得 φ(x))x∈Ω,u∈Rn,h∈RnN, 定义1 称函数u∈W1,r(Ω)(max{1,p-1}≤r≤p)为方程(1)的很弱解,若对所有的φ∈C0∞(Ω)都有 (2) 由于A-调和方程能够反映实际生活中和物理学中众多现象而被广大的专家学者所关注.在数学中关于A-调和方程的研究主要集中在对其解的性质,尤其是对经典弱解的存在性、唯一性、稳定性以及正则性等方面的研究[1-2]. 但是他们所考虑的经典弱解和很弱解之间的联系的这些A-调和方程中,A-调和算子都是和很弱解u无关的.受到这些问题的启发,本文中主要考虑A-调和算子和很弱解u有关的二阶非齐次A-调和方程(1)很弱解的正则性.这些结论都是在方程(1)很弱解存在的前提条件下进行的,有关A-调和方程很弱解的存在性,在文献[10]中有着详细的证明,在这里不做讨论,直接证明很弱解的正则性问题并得到以下结论. 引理2[12-13]设u(x)∈Lp(BR),BR⊂Ω,f∈Lt(BR),t>p并且满足如下不等式: θBRdx+BRdx. (3) 其中C′=C′(n,p,K,θ). (4) (5) (6) 令 (7) 则由一个基本的关系式 0<ε<1,X,Y∈Rn (8) 得到 (9) 取Hodge分解中的φ为弱解定义中的检验函数,于是 (10) 即 I4+I5. (11) 其中 先估计式(11)左边,由假设条件(i)得到 由η的定义可得 (12) 下面估计I1,由条件(iii)和式(9)可得 (13) 其中 由η的定义可得 令 由Hölder不等式可得 (14) 由Young不等式可得 注意到η的定义,则由Hölder不等式可得 (15) 下面对α分情况讨论. 情形1 当 0<α<1 时,由Young不等式可得 综上, 由Hölder不等式、Poincre不等式和Young不等式,得 (16) 因此 (17) 下面估计I2,由假设条件(iii)、Hölder不等式和式(6),可得 K1+K2+K3. (18) 由Hölder不等式以及估计式(6)可得 (19) 由Hölder不等式、Sobolev嵌入定理和估计式(6)可得 (20) (21) 结合估计式(19),(20)和(21)可得 (22) 由Poincre不等式以及η的定义可得 (23) 下面对α的取值范围分情况讨论. 情形1 当0<α≤1时,由Young不等式可得 将上面这些估计式代入I2中,并由Young不等式可得 (24) 下面估计I3.由Hölder不等式、引理2、式(5)和(15)可得 下面估计I4.由式(9)可得 类似J1的估计可知 (25) 下面估计I5.类似I2的估计可知 综合估计式I1-I5和式(12)可得 (26) 整理可得 (27) (28) 即存在r′∈(p-ε,p)⊂(p-ε,+∞),使式(28)成立.下面只须证区间(p-ε,p)是右闭的.实际上,当r′=p时,由引理2以及式(28)可以发现,结论显然成立.故反复应用引理2可得定理的结论. [1] 谢素英,田欢.一类拟线性椭圆型方程弱解关于区域的稳定性[J].应用数学,2009,22(3):566-570. [2] 倪君.关于非齐次A-调和方程解的正则性研究[D].南昌:江西师范大学,2013:26-32. [3] IWANIEC T,SBORDONE C.Weak minima of variational intergrals[J].Reine Angew Math,1994,45:143-161. [4] GRECO L,IWANIEC T,SBORDONE C.Inverting theP-harmonic operator[J].Manusoripta Math,1997,92:249-258. [5] GRECO L,VERDE A.A regularity property ofP-harmonic functions[J].Ann Acad Sci Fenn Ser Math,2000,25:317-323. [6] STROFFOLINI B.A stability result forP-harmonic systems with discontinuous coefficients[J].Electronic J Diff Equ,2001,1(2):1-7. [7] 周树清,文海英,方华强.一类非齐次A-调和方程组很弱解的性质[J].数学物理学报,2003,23A(2):135-144. [8] 佟玉霞,谷建涛,曹建亮.一类非齐次障碍问题很弱解的正则性[J].应用数学,2008,21(1):185-192. [9] 佟玉霞,谷建涛,徐秀娟.一类非齐次A-调和方程很弱解的正则性[J].高校应用学报,2009,24(3):319-323. [10] IWANIEC T,MARTIN G.Geometric function theory and non-linear analysis[M].New York:Oxford University Press,2001:270-280. [11] LI G B,MARTIO O.Stability of solutions of varying degenerate elliptic equations[J].Indiana University Mathematics Journal,1998,47(3):873-891. [12] GIAQUINTA M.Multiple integrals in the calculus of variations and nonlinear elliptic systems[M].Princeton:Princeton University Press,1983:176-185. [13] ELCRAT A,MEYERS N.Some results on regularity for non-linear elliptic systems and quasiregular functions[J].Duke Math J,1975,42:121-136.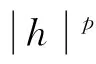
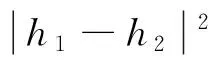
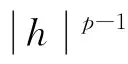
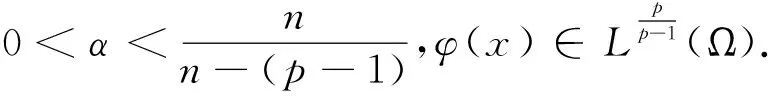
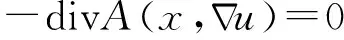

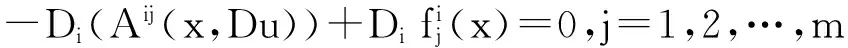
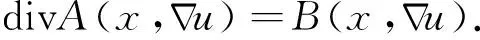
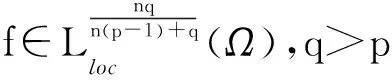
2 基本引理
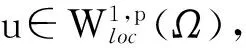
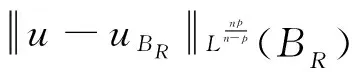
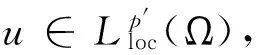
3 定理1的证明