开路和短路电学边界外延铁电薄膜的畴结构及铁电性能

雷俐莎,林晓辉,周志东

(厦门大学 材料学院,福建省特种先进材料重点实验室,福建厦门361005)

外延铁电薄膜具有优良的铁电、压电和介电性能,在微电子和微机械领域应用十分广泛[1]．铁电薄膜的物理特性优于块体铁电材料,这些特性与铁电薄膜的畴结构有密切联系．一个完整的畴结构由畴和畴壁构成,当它处于不同的外加条件下时,如外加电场[2-5]、机械载荷[6-9]、电学边界[10-13]等,畴结构会发生形核和畴壁运动,并形成一个新的畴结构．不同的畴结构对铁电材料的性能会产生很大的影响,所以理解和预测外加条件对铁电畴结构的作用十分重要．

已经有大量的理论和实验研究对不同边界条件下的畴结构进行了分析．Li等[11]基于相场法预测了不同电学边界条件下薄膜的畴结构,通过求解复杂的弹性边值问题得到了弹性能对总自由能的影响,验证了退极化电场和极化强度相互作用对薄膜的畴结构有显著的影响．Junquera等[14]通过第一性原理计算发现表面覆盖电极的BaTiO3铁电薄膜在某个临界厚度下会失去铁电性,指出内电场是其铁电性能不稳定的主要原因．Hong等[12]探讨了表面层和界面层对铁电薄膜畴结构的影响,提出了180°条纹畴是铁电体中弹性能和退极化能共同作用、相互竞争的结果．Xia等[15]的研究表明,电极和铁电薄膜之间存在的“死层”能够诱导产生退极化电场,从而影响畴结构的形成及转变．Zhou等[16]采用开路、短路和中间型电学边界条件分析了铁电薄膜的畴结构演化,发现铁电薄膜在短路电学边界条件下出现180°的条纹畴,在开路电学边界条件下出现多漩涡畴,而在中间型电学边界条件下,因弹性能和退极化能相互竞争,畴结构在180°条纹畴与多漩涡畴之间转变．Tang等[17]在多层PbTiO3薄膜中采用扫描透射电镜(STEM)观察到了周期性排列的漩涡畴结构,并指出在漩涡畴的核心附近有足够大的应力破坏晶格．对于氧化物超晶格铁电薄膜,Yadav等[18]观察到了周期性顺时针和逆时针依次排列的漩涡畴结构．最近,Zhou等[19]提出了一种基于特征函数的非传统相场方法,与传统方法相比,该方法避免了计算过程中需要太多材料参数的弊病,而且能够很好地模拟铁电/多铁材料的微结构演化．事实上,铁电体畴结构的形核、生长、演化和最终的形成过程是各种能量相互竞争和协作的结果．由此可见,界面约束与电学边界条件对铁电体畴结构的形成与翻转有很大的影响,进而影响铁电薄膜的物理性能．

对于多层铁电薄膜结构,目前大多采用系数修正来引入铁电畴翻转产生的本征应力或应变[13,16,20]．Wang等[10]应用有限元方法计算了基体约束对铁电纳米点和铁电薄膜畴变时本征应力的影响,该方法虽适用于任何形状的结构,但较为复杂,一般工程人员不易掌握．而对于一些简单的外延薄膜结构,则可以采用相对简单的应力函数方法求解基体的约束效应．本研究运用应力函数方法分析了基体约束对外延铁电薄膜畴变时本征应力的影响,并结合短路/开路电学边界条件,采用相场法研究了薄膜畴结构的演化和厚度的关系,并分析了极化强度随厚度的变化趋势．

1 铁电体的相场法

本研究基于相场法,结合基体约束和不同的电学边界条件对铁电薄膜畴结构进行分析．铁电材料的总自由能可以表示为

(1)

其中fLD、fG、fdep、felec分别是朗道-德文希尔能量密度、梯度能量密度、退极化能量密度和电场能量密度,V是铁电体的体积．对于钙钛矿型的铁电材料,朗道-德文希尔能量密度的表达式为[16,21]

σ23P2P3).

(2)

其中:Pi为极化强度;α1是介电系数,其表达式为α1=(T-T0)/2ε0c0,T为温度,T0为居里-外斯温度,ε0为真空介电常数,c0为居里常数;α11、α12、α111、α112、α123为高阶介电系数;sij为材料柔性系数;Qij为电致伸缩系数;σij为应力,可以是由于基体和薄膜晶格不匹配引起的错配应力,也可以是由于极化强度改变引起的本征应力．由于畴壁的存在产生了梯度能量密度,它与序参量的梯度有关,其表达式为[22]

P2,1)2+(P2,3+P3,2)2+(P1,3+P3,1)2]+

(P1,3-P3,1)2],

(3)

(4)

(5)

序参量极化强度向量P=(P1,P2,P3)可以通过动态金兹堡-朗道方程[24]来求解:

(6)

其中,δF/δPi(x,t)表示热力学驱动力,x=(x1,x2,x3)是空间位置向量,t为时间,L是动力学系数．

2 二维计算模型的求解方程

2.1 二维模型的相场方程

本研究忽略由于基体和薄膜晶格不同引起的错配,考虑二维计算模型,对生长在基体上的外延铁电薄膜在长度和厚度方向上进行模拟,即仅用到x1和x2方向上的变量,计算简图如图1所示．其中,虚线部分表示计算时考虑的薄膜和基体弹性变形区域,基体的弹性变形部分的厚度为b,薄膜计算区间的长度为l,薄膜厚度为h．假设在虚线以外的区域,不受薄膜畴结构翻转时产生的应力或应变影响,不会产生弹性变形．

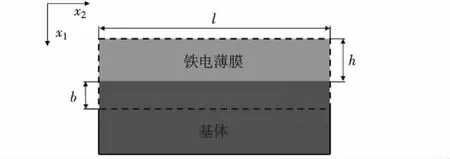
图1 二维铁电体薄膜/基底示意图 Fig.1Schematic diagram of two-dimensional ferroelectric thin film and substrate

为了计算方便,将所有参数进行无量纲处理[10,16,25],即:

(7)

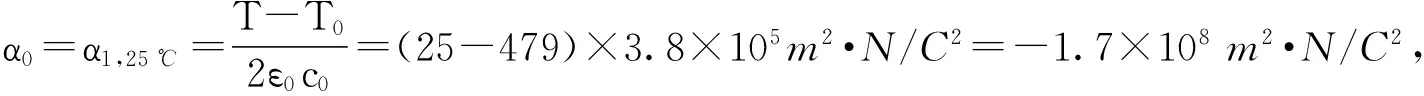
将朗道-德文希尔能量密度、梯度能量密度、退极化能量密度和电场能量密度表达式代入式(6),并运用无量纲化参数,可将动态金兹堡-朗道方程转换成如下微分方程形式[10]:

(8)

(9)

对于式(8)和式(9),在薄膜区间内可以运用有限差分法和四阶龙格库塔法数值求解,其中应力和退极化电场可以通过下述的方法求得．

2.2 本征应力的应力函数解法

(10)

根据弹性理论中的几何关系,总应变和位移的关系为:

(11)

其中:u1、u2分别为x1和x2方向上的位移;ui,j表示ui空间位置j方向的偏导数,i=1,2;j=1,2．在线弹性理论中,应力σij与应变εij应满足物理方程,即:

(12)

(13)

其中,X1、X2分别为x1和x2方向的体积力,此时其值都等于0．根据弹性理论,结构的几何变形应该连续,因此应变εij应该满足变形协调方程(或相容性方程)

(14)

将式(12)代入式(14)可以得到用应力表示的相容性方程

(15)

由平衡方程式(13)可得

(16)

将式(16)代入式(15)的相容性方程得

(17)

表1 数值模拟采用的PbTiO3无量纲参数

Tab.1 The normalized values of PbTiO3 used in the simulations

α*11α*12α*111α*112Q*11Q*12Q*44-0.242.50.491.20.05-0.0150.038s*11s*12s*44G*11G*12G*44G'*447.9×10-4-2.5×10-48.9×10-42011

(18)

2.3 电学边界条件

3 结果和讨论

对图1中的薄膜区域采用20×80的网格进行划分,基体中仅考虑图中虚线部分的弹性变形,采用b/h=0.6进行划分，因此基体部分用12×80的网格进行划分．每一个网格的尺寸为Δx1=Δx2=(h+b)/32,时间步长为Δt*=0.004,其中“*”代表无量纲化的参数,步数为1×104．对于所有的计算过程,使用相同的微小高斯随机值给薄膜区域上每个节点的极化强度赋初值,基体内所有的极化强度始终为零．在长度x2的左右边界上采用周期性边界条件;在薄膜表面与界面上采用开路和短路电学边界条件;在上自由表面采用应力自由的力学边界条件;在薄膜/基体界面采用应力连续的力学边界条件;在基体下边界,考虑薄膜的极化强度改变引起的应力对此处的影响可以忽略,因此采用应力自由的力学边界条件;对于极化强度,在边界和界面上采用零边界条件[27],即上表面和界面的P1=0，P2=0．表1为求解过程中采用的PbTiO3无量纲参数[28-29]．

3.1 短路电学边界条件下的畴结构

图2 短路电学边界条件下不同厚度(9.0 nm(a)和9.5 nm(b))薄膜的畴结构 Fig.2The domain structures of different thicknesses (9.0 nm(a) and 9.5 nm(b)) of films under short circuit electrical boundary condition

图3 开路电学边界条件下不同厚度(19.0 nm(a)和19.5 nm(b))薄膜的畴结构 Fig.3The domain structures of different thicknesses (19.0 nm(a) and 19.5 nm(b)) of films under open circuit electrical boundary condition

当薄膜表面和界面上覆盖电极时,畴结构的变化会使得电荷在电极表面重新分布,进而在电极表面会有电荷补偿．表面的电荷补偿会减小薄膜内退极化电场与退极化能量场．图2给出了厚度为9.0和9.5nm的PbTiO3外延铁电薄膜在短路电学边界条件下用极化强度矢量表示的畴结构形貌(只给出铁电薄膜部分)．如图2(a)所示,9.0nm厚铁电薄膜内只出现水平畴结构;当薄膜厚度为9.5nm时,薄膜内畴结构由水平单畴转变为a/c/a多畴结构,并且在a畴和c畴之间形成了90°的畴壁(图2(b))．形成a/c/a多畴的主要原因是由于薄膜中弹性能随着厚度增加而减小．当薄膜厚度低于9.5nm时,仅出现水平单畴而不是多畴结构,其原因是当薄膜厚度较小时,基体能够约束薄膜内由于极化强度改变而产生的本征应力．在相同的边界条件下,Wang等[10]应用有限元的方法计算了薄膜的本征应力,并结合相场法计算得到PbTiO3铁电薄膜由水平单畴转变为a/c/a多畴的转变厚度为8nm,本研究的计算结果与其相差不大．由此可见,采用较为简单的应力函数法求解薄膜由于极化强度改变产生的本征应力是合理的．

3.2 开路电学边界条件下的畴结构

图4 开路电学边界条件下19.5 nm厚薄膜内归一化本征应力 Fig.4The normalize deigen stresses of the 19.5 nm film under open circuit electrical boundary condition

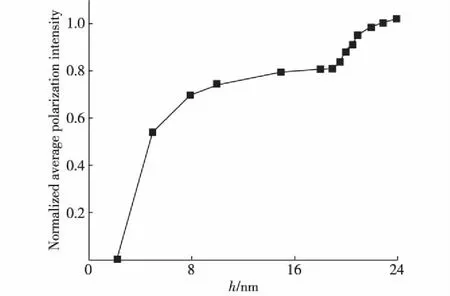
图5 开路电学边界条件下归一化平均极化强度随薄膜厚度变化的曲线 Fig.5The relation between normalized average polarization intensity and film thickness under open-circuit electrical boundary condition

4 结 论

本研究采用弹性理论中的应力函数法求解铁电薄膜内由于极化强度改变与基体约束引起的本征应力,并结合相场法分析了短路和开路电学边界条件下外延铁电薄膜的畴结构与极化强度．对短路电学边界条件下畴结构的计算结果显示,存在水平a单畴到a/c/a多畴结构转变的临界厚度,与现有采用有限元方法的文献[10]结果对比,证明了采用应力函数法具有一定的正确性,而且简单,易操作,便于工程技术人员掌握并可以解决简单的工程计算．进一步采用该方法求解开路电学边界条件下的畴结构、应力分布和平均极化强度,讨论了退极化电场和基体约束对薄膜畴结构和铁电性能的影响,发现畴结构出现漩涡多畴结构与水平单畴结构的分层形式,指出其原因在于:靠近基体边界存在压缩应力,靠近自由表面存在拉伸应力,而基体约束产生的压缩应力与退极化场竞争导致漩涡多畴结构出现．通过研究薄膜平均极化强度随厚度的变化,找到了开路电学边界条件下顺电相向铁电相转变的临界厚度和水平单畴向漩涡多畴转变的临界厚度．

[1]SCOTTJF.Devicephysicsofferroelectricmemories[J].Ferroelectrics,1996,183(1):51-63.

[2]LAIBK,PONOMAREVAI,NAUMOVII,etal.Electric-field-induceddomainevolutioninferroelectricultrathinfilms[J].PhysicalReviewLetters,2006,96(13):137602.

[3]NELSONCT,GAOP,JOKISAARIJR,etal.Domaindynamicsduringferroelectricswitching[J].Science,2011,334(6058):968-971.

[4]SANDOD,BARTHELEMYA,BIBESM.BiFeO3epitaxialthinfilmsanddevices:past,presentandfuture[J].JournalofPhysics:CondensedMatter,2014,26(47):473201.

[5]CAOGP,CAOY,HUANGHB,etal.Analysisofmulti-domainferroelectricswitchinginBiFeO3thinfilmusingphase-fieldmethod[J].ComputationalMaterialsScience,2016,115:208-213.

[6]PERTSEVNA,ZEMBILGOTOVAG,TAGANTSEVAK.Effectofmechanicalboundaryconditionsonphasediagramsofepitaxialferroelectricthinfilms[J].PhysicalReviewLetters,1998,80(9):1988-1991.

[7]QIAOH,WANGJ,CHENWQ.Phasefieldsimulationofdomainswitchinginferroelectricsinglecrystalwithelectricallypermeableandimpermeablecracks[J].ActaMechanicaSolidaSinica,2012,25(1):1-8.

[8]WANGJ,LIYL,CHENLQ,etal.Theeffectofmechanicalstrainsontheferroelectricanddielectricpropertiesofamodelsinglecrystal-phasefieldsimulation[J].ActaMaterialia,2005,53(8):2495-2507.

[9]PERANTIEJ,STRATULATMS,HANNUJ,etal.Enhancingpolarizationbyelectrode-controlledstrainrelaxationinPbTiO3heterostructures[J].APLMaterials,2016,4(1):016104.

[10]WANGJ,ZHANGTY.Sizeeffectsinepitaxialferro-electricislandsandthinfilm[J].PhysicalReviewB,2006,73(14):144107.

[11]LIYL,HUSY,LIUZK,etal.Effectofelectricalboundaryconditionsonferroelectricdomainstructuresinthinfilms[J].AppliedPhysicsLetters,2002,81(3):427-429.

[12]HONGL,SOHAK,SONGYC,etal.Interfaceandsurfaceeffectsonferroelectricnano-thinfilm[J].ActaMaterialia,2008,56(13):2966-2974.

[13]MADC,ZHENGY,WOOCH.Phase-fieldsimulationofdomainstructureforPbTiO3/SrTiO3superlattices[J].ActaMaterialia,2009,57(16):4736-4744.

[14]JUNQUERAJ,GHOSEZP.Criticalthicknessforferroelectricityinperovskiteultrathinfilms[J].Nature,2003,422(6931):506-509.

[15]XIAYX,WANGJ.Switchingbehaviorofferroelectricthinfilmswithdeadlayers[J].SmartMaterialandStructures,2012,21(9):18-21.

[16]ZHOUZD,WUDY.Domainstructuresofferroelectricfilmsunderdifferentelectricalboundaryconditions[J].AIPAdvances,2015,5(10):107206.

[17]TANGYL,ZHUYL,MAXL,etal.Observationofaperiodicarrayofflux-closurequadrantsinstrainedferroelectricPbTiO3films[J].Science,2015,348(6234):547-551.

[18]YADAVAK,NELSONCT,HSUSL,etal.Observationofpolarvorticesinoxidesuperlattices[J].Nature,2016,530(7589):198-201.

[19]ZHOUYG,PENGJL,PANK,etal.Anunconventionalphasefieldmodelingofdomainsformationandevolutionintetragonalferroelectrics[J].ScienceChinaTechnologicalSciences,2016,59(7):1059-1064.

[20]QIUQY,MAHJOUBR,ALPAYSP,etal.Misfitstrain-filmthicknessphasediagramsandrelatedelectromechanicalpropertiesofepitaxialultra-thinleadzirconatetitanatefilms[J].ActaMaterialia,2010,58(3):823-835.

[21]HAUNMJ,FURMANE,JANGSJ,etal.Thermo-dynamictheoryofPbTiO3[J].JournalofAppliedPhysics,1987,62(8):3331-3338.

[22]CHENWJ,ZHENGY,WANGB,etal.Coexistenceoftoroidalandpolardomainsinferroelectricsystems:strategyforswitchingferroelectricvortex[J].JournalofAppliedPhysics,2014,115(21):214106.

[23]LIYL,HUSY,LIUZK,etal.Effectofelectricalboundaryconditionsonferroelectricdomainstructuresinthinfilms[J].AppliedPhysicsLetters,2002,81(3):427-429.[24]XUEF,WANGJJ,SHENGG,etal.PhasefieldsimulationsofferroelectricsdomainstructuresinPbZrxTi1-xO3bilayers[J].ActaMaterialia,2013,61(8):2909-2918.

[25]WANGJ,SHISQ,CHENLQ,etal.Phase-fieldsimulationsofferroelectric/ferroelasticpolarizationswitching[J].ActaMaterialia,2004,52(3):749-764.

[26] 刘土光,张涛.弹塑性力学基础理论[M].武汉:华中科技大学出版社,2008:119.

[27]VENDIKOG,ZUBKOSP.Ferroelectricphasetransitionandmaximumdielectricpermittivityofdisplacementtypeferroelectrics(BaxSr1-xTiO3)[J].JournalofAppliedPhysics,2000,88(9):5343-5350.

[28]CHENZY,SUYX,ZHOUZD,etal.TheinfluenceoftheelectricalboundaryconditionondomainstructuresandelectrocaloriceffectofPbTiO3nanostructures[J].AIPAdvances,2016,6(5):055207.

[29]ZHOUZD,LEILS,SUYX.Theeffectofthesurfaceelectrodedistributionsondomainstructuresofferro-electricthinfilms[J].AIPAdvances,2017,7(6):065019.

[30]PETRARUA,PERTSEVNA,KOHLSTEDTH,etal.Polarizationandlatticestrainsinepitaxialfilmsgrownbyhigh-pressuresputtering[J].JournalofAppliedPhy-sics,2007,101:114106.

[31]ZHOUZD,ZHANGCZ,JIANGQ.Effectofelectromechanicalboundaryconditionsonthepropertiesofepitaxialferroelectricthinfilms[J].ChinesePhysicsB,2011,20:107701.

[32]KIMDM,EOMCB,NAGARAJANV,etal.ThicknessdependenceofstructuralandpiezoelectricpropertiesofepitaxialPb(Zr0.52Ti0.48)O3filmsonSiandSrTiO3substrates[J].AppliedPhysicsLetters,2006,88(14):142904.

[33]PALOVAL,CHANDRAP,RABEKM.Modelingthedependenceofpropertiesofferroelectricthinfilmonthickness[J].PhysicalReviewB,2007,76(1):014112.