基于滞环比较的扰动观测法在光伏MPPT中的研究
代相波,赵志刚
(沈阳工程学院 a.研究生部;b.电力学院,辽宁 沈阳 110136)
最大功率点跟踪(Maximum Power Point Tracking,MPPT)是指通过一定技术手段,使光伏电池始终工作在最大功率点(Maximum Power Point,MPP)附近[1-4],以实现最高效的能源利用。当前,利用较为广泛的MPPT技术为扰动观测法[5],该方法被控参数少、算法简单,但实际应用中,如果系统已处于MPP处,其仍会变工作点进行下一步跟踪判断,易发生误判。因此,提出一种基于滞环比较的变步长扰动观测法,利用恒定电压法CVT(Constant Voltage Tracking)[6]使得启动迅速,通过滞环比较法[7]判断跟踪方向,通过功率预测法决定跟踪步长。
1 光伏电池输出特性
1.1 光伏电池模型
光伏电池的基本原理是光生伏特效应,P-N结是其工作核心。理想光伏电池由光生电流源和一个并联二极管得到,考虑到实际内部损耗,可通过在理想模型中增加串联电阻和并联电阻来模拟,如图1[8]所示。
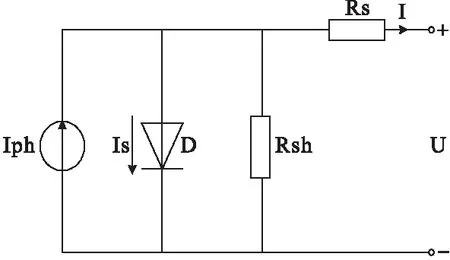
图1 光伏电池等效电路
由该模型给出的光伏电池伏安特性为
(1)
式中,U为光伏电池输出电压;I为光伏电池输出电流;Iph为光生电流源;Is为二极管饱和电流;q为电子电量常量,取1.602×10-19C;k为玻尔兹曼常量,为1.381×1023J/K;T为光伏电池工作绝对温度值;A为二极管特性拟合系数,取值在1~2之间,在大电流时取值靠近1,小电流时取值靠近2,一般取为1.3。
文献[9]提出了一种适合工程应用的仿真模型,仅需要开路电压、最大功率点电压、短路电流、最大功率点电流等参数即可实现。其输出伏安特性可表示为
(2)
在实践应用标准测试条件下(S=1 000 W/m2、T=25 ℃),UOC、Um、Isc、Im等参数在太阳板的出厂参数中均已标记,对于同一型号产品为常数,故C1和C2亦为常数。
当光照强度或环境温度发生变化时,需要调整新条件下的 4 个参数, 即Isc-new、Im-new、Uoc-new、Um-new[3],从而计算出当前条件下的C1-new、C2-new,具体表示如下:
(3)
单晶硅光伏电池中,a、b、c的典型取值分别为a=0.002 5/℃,b=0.5,c=0.002 88/℃。
结合上述光伏电池工程实践应用模型,在Matlab/Simulink软件中搭建仿真模型,如图2所示。参数设置参考型号为CRM250S156P-60(T)的光伏电池,Pm=250 W、Isc=8.56 A、Im=8.06 A、Uoc=37.8 V、Um=31.0 V,a、b、c均取典型值。
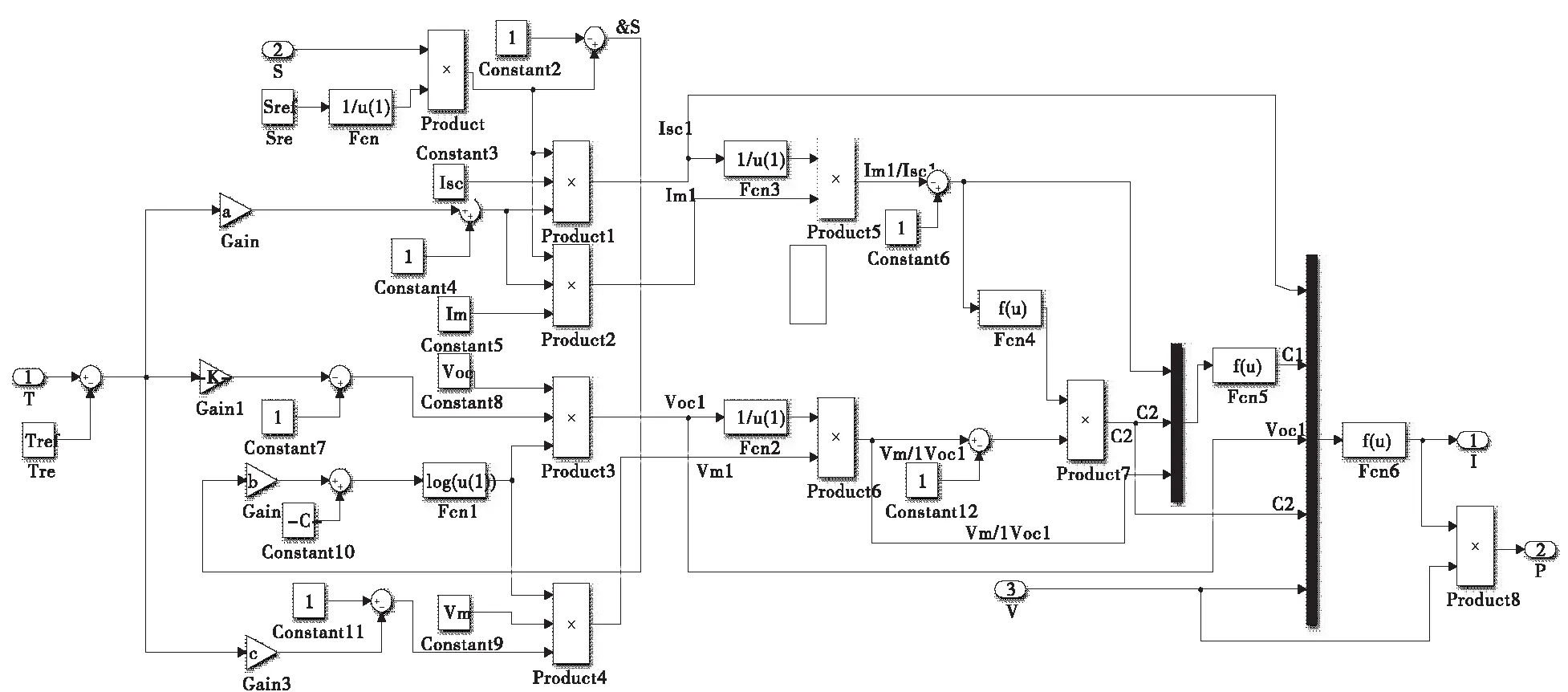
图2 光伏电池仿真模型
1.2 光伏电池输出特性曲线
同一负载条件下光伏电池的输出特性主要受光照强度和环境温度的影响[10],图3、图4给出了PV仿真模型在光照强度和环境温度变化时的P-U曲线。
由图3和图4可以看出,在恒定光照强度下,随着环境温度的升高,Isc增大,而UOC却不断降低,Pm逐渐下降,Im缓慢增大,Um缓慢降低;在恒定环境温度下,随着光照强度的增大,Isc、UOC均增大,Pm逐渐增大,Im、Um也增大。
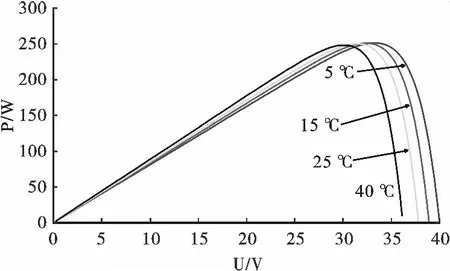
图3 温度对P-U曲线的影响
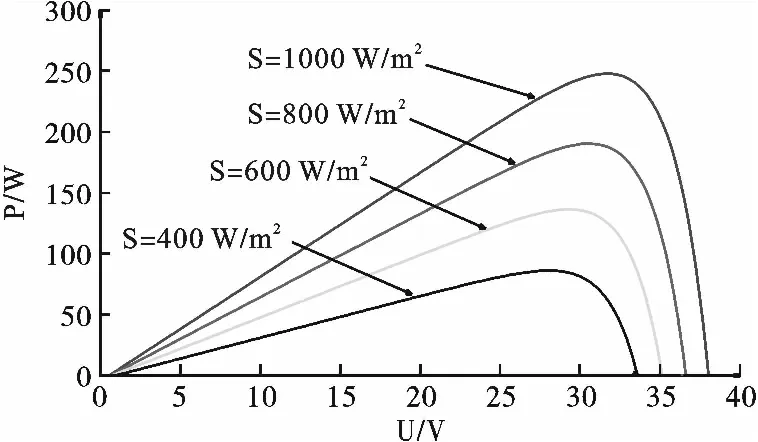
图4 光照强度对P-U曲线的影响
综合上述,在Matlab/Simulink环境下搭建的光伏电池模型可以较好的反应光伏特性,并可根据标准状况下Isc、UOC、Im、Um等参数,模拟任意光照及环境温度下的输出情况,物理意义明确,有较高的通用性。
2 传统扰动观测法原理分析
扰动观测法是MPPT领域应用最为广泛的一种控制方法。其基本工作原理是周期性地对光伏电池输出电压施加扰动,然后通过计算P=I×U来观测输出功率的变化方向。如输出功率增加,则继续在输出电压该方向上施加扰动,反之则反向施加。扰动观测法的算法流程如图5所示。其中,Uk、Ik为光伏电池当前的电压电流值,Uk-1、Ik-1为上一步光伏阵列的电压及电流值,U*为整流器(实用BOOST电路)电压控制信号参考值。
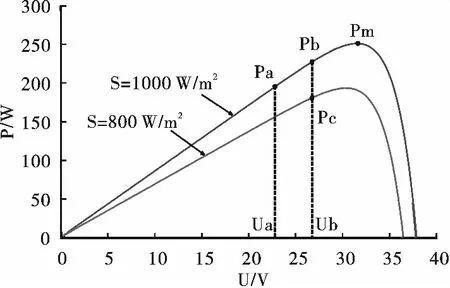
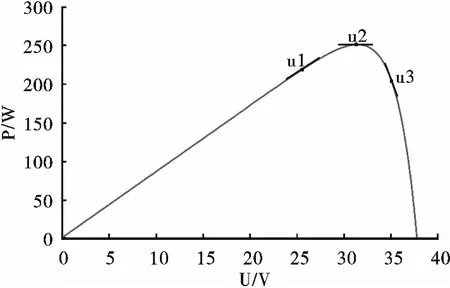
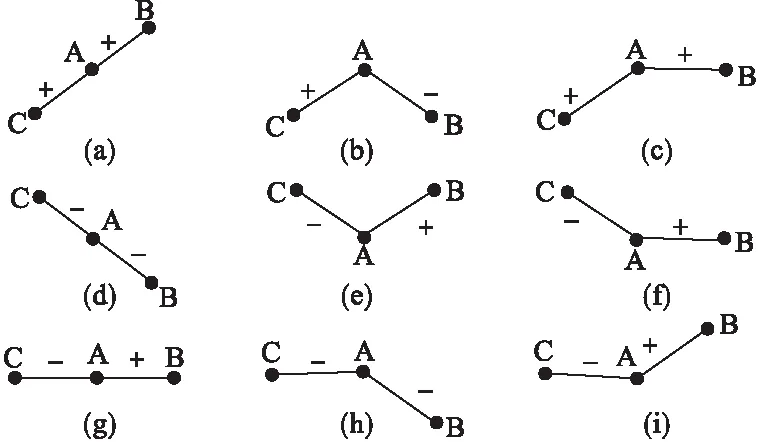
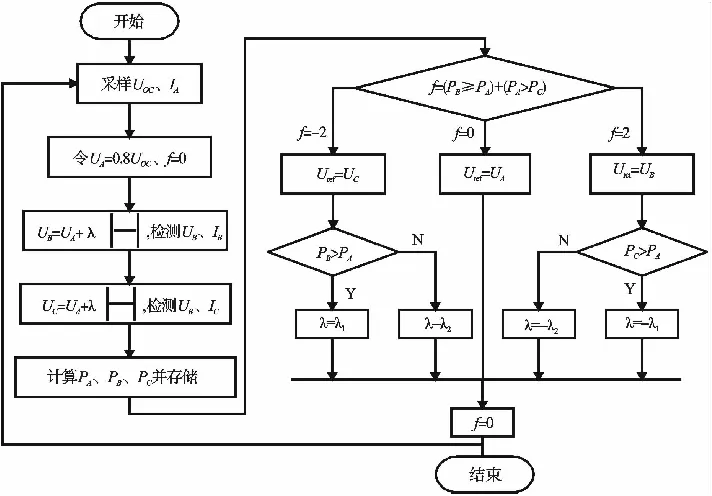
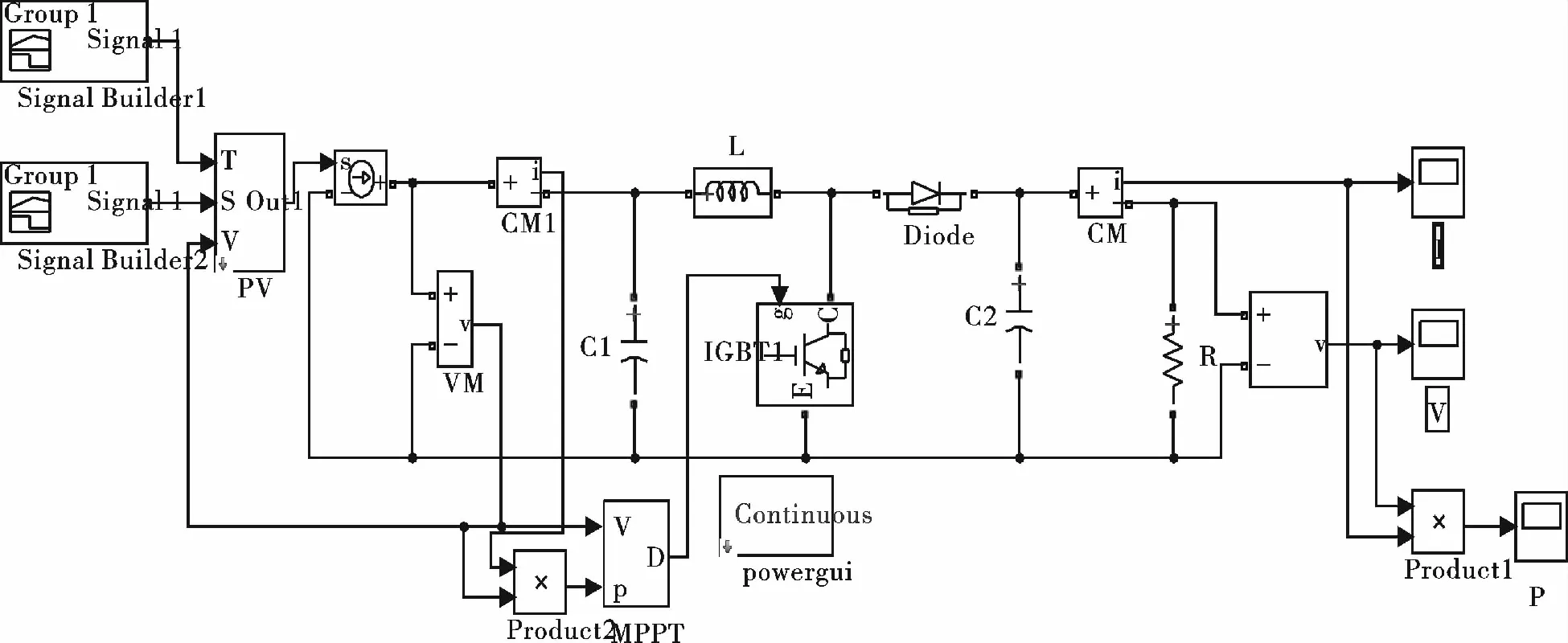
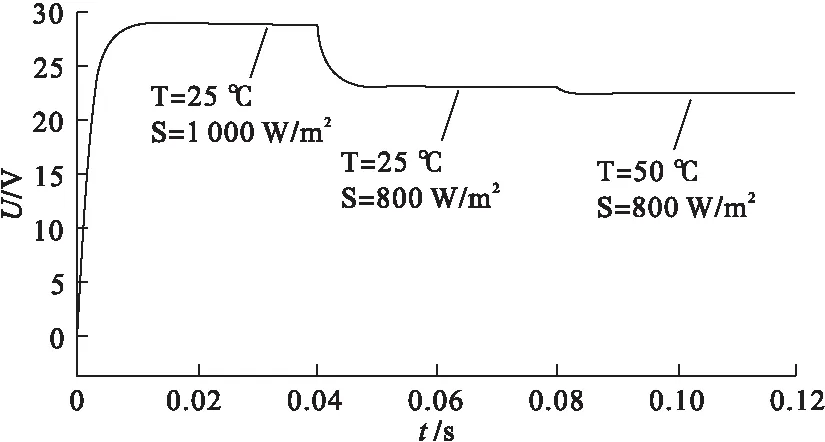
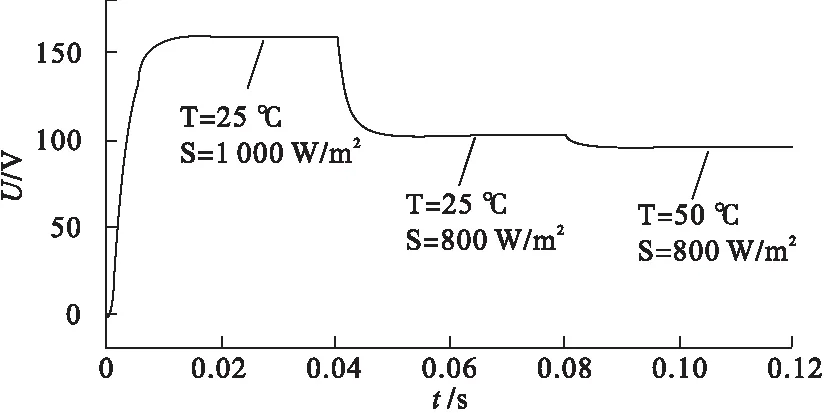
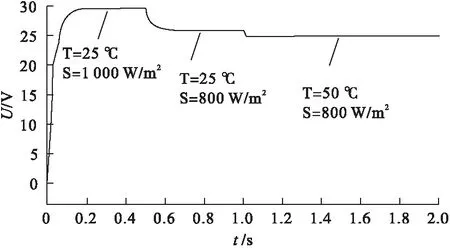
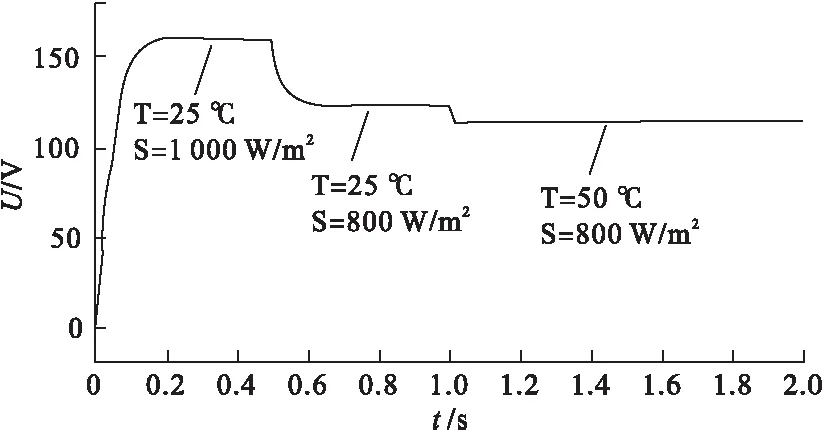
图6为扰动观察法误判示意图。通过图6分析可知,采用扰动观察法进行MPPT,当光伏电池工作在Ua点时,此时输出功率为Pa,如果施加正方向的扰动,当外界条件无变化时,输出功率为Pb,系统向Pm方向逐渐增大;但如果此时光照强度降低,则系统输出功率降至Pc处,则在Ub点对应输出功率Pc 图5 扰动算法流程 图7为光伏板P-U曲线切线图,dP/dU曲线有如下特点: 图6 扰动观察法误判 (4) (5) 图7 光伏点P-U曲线切线 滞环比较法[11]是设当前工作点为A点,并以该点为中心,于该点两侧等距离处各取一点B和C构成滞环。以A点为初始值,依据扰动方向扰动至B点,再反向两个步长扰动至C点。比较A、B、C三点处功率PA、PB、PC,记PA>PC为“+”,PB≥PA为“+”,其余情况均为“-”,则共有9种情况,如图8所示。 图8 滞环比较法A、B、C三点功率关系 比较图8中的PA、PB、PC,可以得出电压扰动的3种规则: 规则1:两次扰动功率比较均为“+”,电压值扰动方向不变; 规则2:两次扰动功率均为“-”,电压值向相反方向扰动; 规则3:两次扰动功率比较有“+”有“-”,电压值维持不变。 分析上述3种规则可以看出,滞环比较法是通过双向扰动来确认扰动方向,电压到达MPP处即停止扰动,避免了误判现象的发生。如果将该方法与基于功率预测的变步长扰动法结合,则可以同时提高跟踪速度与精度,并较好的避免误判,抑制MPP处的功率振荡。 分析上述2种算法,结合功率预测与滞环比较2种方法的优点,提出一种新型扰动观测法,具体流程如图9所示。 图9 基于滞环比较的变步长扰动观测法 采用恒定电压CVT(Constant Voltage Tracking)启动,由CVT可知MPP处的电压约为0.76UOC[12],令UA=0.8UOC,采样UA、IA,通过施加扰动计算UB、UC、IB、IC,并计算功率。根据图9所示滞环比较法A、B、C功率关系,计算标志位f的结果, 根据f值判断下一步的扰动方向,并根据当前值改进扰动量的大小。 Matlab/Simulink仿真环境搭建如图10所示。仿真时间为0.12 s,使用变步长ode23t进行仿真,相对误差设置为1×10-4,其余均设置为auto。 起始外界环境为T=25 ℃、S=1 000 W/m2,光照强度在0.04 s时突变到S=800 W/m2,温度在0.08 s时突变到T=50 ℃,如图11、12所示。电池在输出电压为0.02 s时就可以达到稳定,CVT启动的优势得到充分体现。当外界环境发生突变时,系统仍能够在0.02 s内跟踪到最大功率点处。 图13、14为传统扰动观测法的仿真效果,通过对比可以看出,基于滞环比较的变步长扰动观测法跟踪速度大幅提升,由0.15 s提升到不到0.02 s,且在MPP处振幅减小。 图10 新型扰动观测法Matlab/Simulink仿真 图11 改进方法电压输出 图12 改进方法功率输出 图13 传统方法电压输出 图14 传统方法功率输出 1)分析了光伏电池的特性,并建立了光伏电池实用仿真模型,通过Matlab/Simulink仿真得出了光伏电池在光照强度与环境温度变化下的输出特性变化规律。 2)分析了扰动观测法工作原理,提出了一种基于滞环比较的新型扰动观测法,通过Matlab/Simulink仿真表明了该方法相对于传统扰动观测法启动速度快,在外界光照强度及环境温度发生变化时均能够迅速跟踪,且MPP处震荡幅度小,改善了光伏MPPT跟踪速度与跟踪精度之间的矛盾,证明了该算法的可行性。 [1] 刘雅莉.基于分布式光伏发电系统最大功率点跟踪特性研究[D].昆明:云南师范大学,2014. [2] 潘 伟.单相双级独立式光伏逆变器的研究[D].青岛:青岛大学,2013. [3] 郑义斌.光伏发电系统最大功率跟踪与并网控制方法[D].成都:西南交通大学,2016. [4] 魏 单,陈 琳.“农光互补”光伏电站设计[J].沈阳工程学院学报:自然科学版,2017,13(2):108-112. [5] 刘 飞,段善旭,殷进军,等.单级式光伏发电系统MPPT的实现与稳定性研究[J].电力电子技术,2008,42(3):28-30. [6] 张 林,郭前岗,周西峰.一种新型光伏系统MPPT变步长滞环比较P&O法[J].电测与仪表,2014,51(2):27-31. [7] 艾永乐,李 瑞.滞环比较器及其在电力电子中的应用[J].汕头大学学报:自然科学版,2008,23(4):71-75. [8] 王成山.微电网分析与仿真理论[M].北京:科学出版社,2013. [9] 焦 阳,宋 强,刘文华.光伏电池实用仿真模型及光伏发电系统仿真[J].电网技术,2010,34(11):198-202. [10] 肖文波,吴华明,傅建平,等.光强和温度对硅光伏电池输出特性的影响[J].华中科技大学学报:自然科学版,2017,45(1):108-112. [11] Qi Ping-yuan.The dual-mode maximum power point tracking control method based on improved variable step size[J].Advanced Materials Research,2012,38(3):1624-1627. [12] 荣德生,刘 凤.改进型扰动观察法在光伏MPPT中的研究[J].电力系统及其自动化学报,2017,29(3):104-109.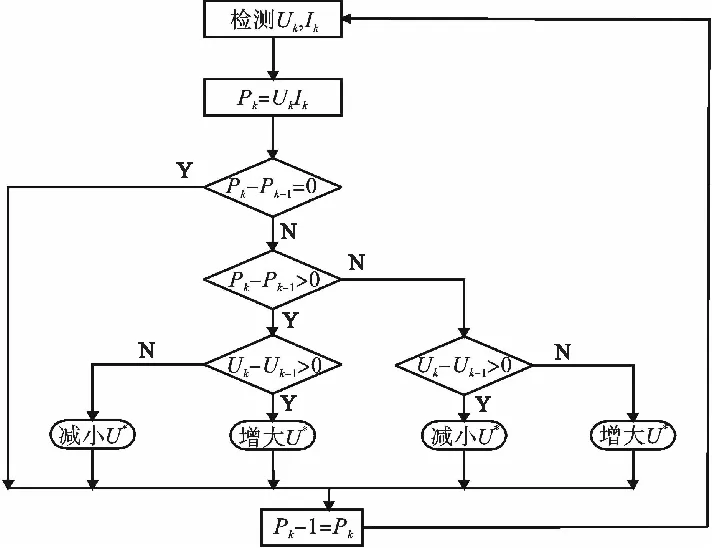
3 基于滞环比较的变步长扰动观测法
3.1 基于功率预测的变步长扰动观测法

3.2 滞环比较法原理
3.3 基于滞环比较的变步长扰动观测法
4 结 论

