ANFIS与模糊聚类—ESN的光伏发电功率预测模型比较
王大虎+贾倩+林红阳


摘要:光伏电站的发电功率高度依赖于不同的天气条件,其变化无规律可循,从而给电网管理带来挑战。因此,对光伏发电功率进行预测研究,以确保电网安全、稳定运行。首先,按季节和天气类型划分历史发电数据,经数据分析后,将温度与历史发电功率作为输入,构建了ANFIS与模糊聚类-ESN两个光伏发电功率预测模型。利用Matlab模糊逻辑工具箱构建ANFIS模型,而对于模糊聚类-ESN模型的构建,先采用模糊聚类处理输入数据,再利用ESN进行训练与预测。通过对两个预测结果的比较,模糊聚类-ESN模型的预测精度高于ANFIS模型。
关键词:自适应神经模糊推理系统;模糊聚类;回声状态网络;光伏发电功率预测
DOIDOI:10.11907/rjdk.172090
中图分类号:TP319
文献标识码:A文章编号文章编号:1672-7800(2018)001-0157-05
Abstract:Power generation output of a PV plant is highly dependent on different weather conditions, but its changes are irregular, which pose a challenge to grid management. For this, scholars to predict the photovoltaic power generation to ensure that the grid safe and stable operation. In this paper, the historical power generation data is divided directly by season and weather type. After the data analysis, take the temperature and historical power generation as input. Two photovoltaic power generation models, the adaptive neural fuzzy reasoning system (ANFIS) and the fuzzy clustering-ESN, are constructed. ANFIS model is constructed by Matlab fuzzy logic toolbox. The construction of fuzzy clustering-ESN model is used to process the input data with fuzzy clustering, and then ESN is used to train and predict. Comparing the two prediction results, the fuzzy clustering-ESN model has higher prediction accuracy than ANFIS model.
Key Words:adaptive neuro-fuzzy inference system(ANFIS); fuzzy clustering; echo state network(ESN); photo-voltaic power generation prediction
0引言
环境污染与资源短缺带来的压力,迫使全球范围内进入可持续发展时代,环境友好型的可再生能源利用受到各国政府的高度重视。光伏发电作为继水力发电、风力发电等可再生能源的一种形式,其发展对经济、社会和环境都具有积极影响。目前,国内外已经建立了大量大规模的光伏发电系统,但因光伏发电系统的输出易受太阳辐射强度和天气等不确定因素影响,使其具有随机性和间接性,导致光伏发电系统无法稳定运行[1-3]。近年来,随着兆瓦级光伏发电系统并网运行的增加,电网的安全、稳定运行更加受到重视。因此,对光伏发电系统输出功率的随机性进行准确预测,进而对电网调度进行合理安排显得尤为重要。
人工神经网络(Artificial Neural Networks,ANN)已被广泛应用于光伏发电功率预测中。回声状态网络是基于储蓄池的计算网络,是ANN的一种类型,在光伏发电功率预测方面也取得了一定成果[4-6]。光伏发电功率数据是不确定、无规律可循的,为得到更准确的预测结果,需在预测前对数据进行处理,使其具有一定规律。文献[5]、[7-9]通过经验模态分解(EMD)方法对历史数据进行处理,得到不同尺度的模态分量和趋势分量数据后,对数据建立预测模型;文献[6]、[10-12]通过聚类算法将光伏发电功率历史数据划分为若干类,再通过分类识别找出与预测日最相似的一类历史数据集进行预测。利用以上的数据处理方法都得到了较准确的功率预测值。ANFIS是神经网络自适应能力和模糊系统推理能力的集成,可从数据集中开发出模糊推理系统,再通过神经网絡建立相应模型。采用ANFIS对光伏发电功率进行预测是一个合适的方法[13-14]。
本文将构建ANFIS和聚类-ESN两个预测模型,通过分析历史光伏发电功率的影响因素,可直接将数据按季节和天气类型进行划分,最终将温度作为变量与历史数据一同输入。可直接利用Matlab模糊逻辑工具箱实现ANFIS预测模型,而对于聚类-ESN预测模型,采用模糊聚类算法处理输入数据后,利用回声状态网络对数据进行训练与预测。通过比较两个模型的预测值,选择出预测精度更高的预测模型。
1光伏发电功率输入变量确定
光伏发电的核心是通过光伏电池组件,将光能直接转换成电能,其输出功率为:
其中,Ps为单位面积的光伏系统输出功率,η为光伏阵列的转换效率,S为光伏阵列的总面积,Ir为光伏阵列接收的太阳辐射强度,Tc为光伏组件板温度。endprint
在某光伏电站中光伏阵列的转换效率、总面积等是确定的,由上式可知,影响光伏发电功率的主要变量因素为太阳辐射强度和光伏组件温度,其中光伏组件温度主要受环境温度影响。
1.1光伏发电功率太阳辐射强度影响
太阳辐射强度的变化对光伏发电功率的影响十分显著,如图1所示。
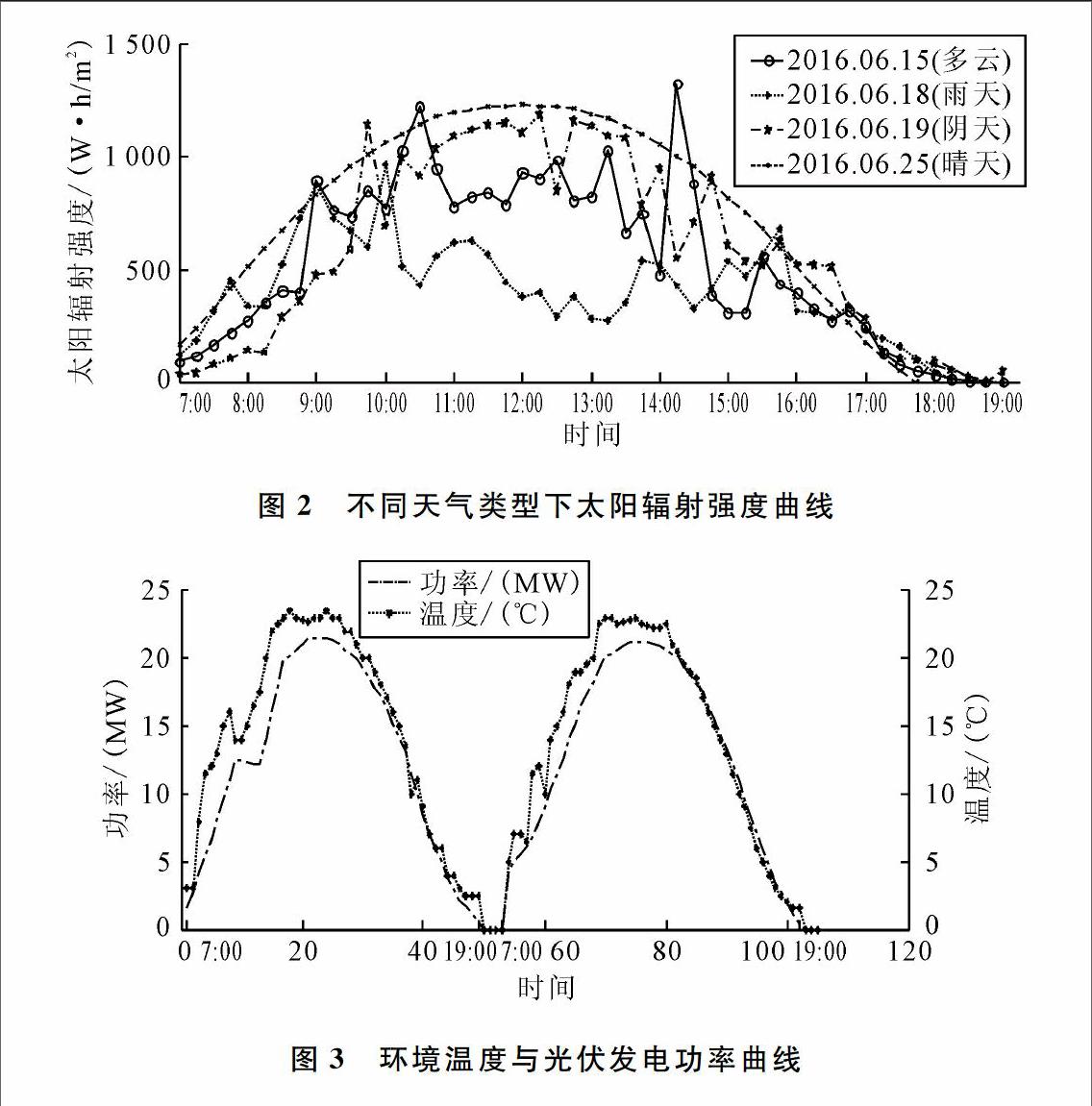
由图1可知,光伏发电功率随着太阳辐射强度的增加而增大,呈现对应关系。因此,需将太阳辐射强度作为光伏发电功率的一个输入变量。但因我国辐照观测点较少,获取辐射强度数据较为困难,为解决这一难题,考虑天气类型与太阳辐射强度的相应关系,文献[15]、[16]采用天气类型代替太阳辐射强度。图2为不同天气类型下太阳辐射强度的相关曲线。
由图2得出,不同天气类型下,太阳辐射强度差异较大。天气类型为晴天时,太阳辐射强度曲线波动平稳,有明显规律;在其它天气类型时,太阳辐射强度曲线波动较大,无明确规律。因此,可将历史数据按天气类型进行筛选作为输入变量,以取代太阳辐射强度的变化。
1.2光伏发电功率温度影响
环境温度的变化对光伏发电功率也存在影响,如图3所示。
由图可知,当环境温度在一定范围内变化时,光伏发电功率随着环境温度发生相应变化,但当环境温度达到某一临界点时,温度继续升高,光伏发电功率反而下降。这是因为环境温度会直接影响光伏阵列板的温度,环境温度越高,光伏阵列板的温度也越高,导致发电性能下降[17]。
综合以上影响光伏发电功率的因素,将环境温度和天气类型作为预测光伏发电功率的变量,又因天气类型可通过天气预报得出,在变量输入前可直接对其分类,则本文的预测输入变量为环境温度,其包括最高温度Tmax、最低温度Tmin与平均温度Tmean。
2ANFIS预测模型
2.1自适应模糊推理系统
自适应网络模糊推理系统(ANFIS)是将神经网络的学习机制和模糊系统的推理能力相结合的自适应系统,由Sugeno[18]最早提出。ANFIS利用神经网络的学习能力,从输入输出数据集中开发模糊推理系统。学习模糊系统的隶属函数参数,可准确跟踪给定的输入和输出集合[19]。为确定模糊系统的最优隶属函数形状,ANFIS建立了一个模糊推理系统(Fuzzy Inference System,FIS),其隶属函数参数通过训练数据在已建立的模糊规则上不断学习、调整,构造出最佳的输入—输出映射[20-21]。
2.2ANFIS预测模型
本文以福建某30MW光伏电站为例,以夏季一天中7:00~19:00每1小时的时间间隔温度为输入变量,包括最高温度Tmax、最低温度Tmin与平均温度Tmean,以预测发电功率P。本节使用Matlab模糊逻辑工具箱实现ANFIS系统,基于其自学习过程,使用混合学习算法调整并获得ANFIS模块的最优隶属函数。算法包括最小二乘法与梯度下降的反向传播法的组合。表1给出了通过训练ANFIS获得的输入/输出变量范围、隸属函数类型和隶属函数。表2为基于规则的模糊推理系统,含有8个规则,3个输入变量的2个隶属函数和1个输出变量的8个隶属函数,输出隶属函数被命名为P1-P8。
图4给出了本节对应的ANFIS结构图。由图可知,ANFIS结构分为5层,且同一层网络的每个节点具有相似功能,用O1,i表示第一层第i个节点的输出,依此类推。该模糊推理系统有3个输入x、y、z分别表示Tmax、Tmin、Tmean,以及一个输出f。
第一层:对输入参数进行模糊化,确定对应模糊集的隶属度:
其中,i由{m,n,l}的相应组合构成,且i=1,2,…,8;Am、Bn和Cl为模糊集,文中表示的模糊意义为温度的“低”和“高”;μAm(x)、μBn(y)和μCl(z)为模糊集的隶属函数,表示x、y、z属于模糊集Am、Bn、Cl的程度。隶属度函数包括:钟形函数、三角形函数、梯形函数及高斯型函数等。
3模糊聚类-ESN预测模型
3.1模糊聚类
聚类是根据“最小化类间相似性,最大化类内相似性”原则,将数据集分类成不同类或簇的过程,即由聚类生成的同一簇中的数据具有很大的相似性,而不同簇间的对象有很大的相异性。聚类分析是研究样品或指标分类问题的一种统计分析方法,同时也是数据挖掘的一个重要算法。聚类分析内容非常丰富,模糊聚类法即是其中一种。
模糊聚类指根据研究对象自身属性构造模糊矩阵,并根据一定隶属度确定聚类关系,即通过模糊数学方法定量确定样本间的模糊关系,从而客观且准确地进行聚类。
通过对光伏发电功率进行分析,将光伏发电功率的历史数据V和温度数据T作为输入样本,表示如下:
其中,P为发电站输出功率的实际值,为预测模型得到的预测值,n为预测样本个数,i为第i个数据点。
图6显示了利用ANFIS和模糊聚类-ESN预测模型获得的连续4天的功率预测结果。表3比较了两种预测模型的准确性。
由图6可以看出,不同天气类型下,ANFIS和模糊聚类-ESN预测模型的预测值相对于实际值的偏差波动大小存在差异。当天气类型处于平稳波动时(如:晴天),偏差较小;当处于波动较大的天气类型时(如:阴、雨、多云),偏差也较大。模糊聚类-ESN模型的功率预测曲线更接近实际功率曲线,明显优于ANFIS预测模型。通过表3的误差对比可知,本文构建的两个预测模型中,ANFIS模型MAE和RMSE的预测误差值约为模糊聚类-ESN模型的两倍,且模糊聚类-ESN模型与ANFIS模型相比,其预测精度提高了47.46%,即得出模糊聚类-ESN模型相比于ANFIS模型具有更高的预测精度。
5结语
本文构建了ANFIS与模糊聚类-ESN的光伏发电功率预测模型,两种预测模型均先对输入数据进行模糊化处理后,传入各自的训练网络中。本文按季节和天气类型对历史光伏发电功率数据进行直接划分,并将温度与划分的数据一同作为预测模型的输入,对网络进行训练与预测。最后,将ANFIS的预测结果与聚类-ESN进行比较,得出模糊聚类-ESN预测模型具有更高的预测精度。endprint
参考文献:
[1]P Y LIM, FARRAH WONG. Photovoltaic power predictions using modified adaptive response rate exponential smoothing method[C]. IEEE International Conference on Sustainable Energy Technologies,2016.
[2]L BIRD, M MILIGAN, D LEW. Integrating variable renewable energy: challenges and solutions[R]. Office of Scientific & Technical Information Technical Reports,2013.
[3]陈亚博,盛戈皞,黎建,等.含光伏和风电的电力系统随即生产模拟[J].电力系统及其自动化学报,2015,27(5):1-6.
[4]I JAYAWARDENE, G K VENAYAGAMOORTHY. Comparison of adaptive neuro-fuzzy inference systems and echo state networks for pv power prediction[J]. Procedia Computer Science,2015,53:92-102.
[5]李多,董海鹰,杨丽霞.基于EMD与ELM的光伏电站短期功率预测[J].可再生资源,2016,34(2):173-177.
[6]李乐,刘天琪.基于近邻传播聚类和回声状态子网络的光伏预测[J].电力自动化设备,2016,36(7):41-46.
[7]高相铭,杨世凤,潘三博.基于EMD和ABC-SVM的光伏并网系统输出功率预测研究[J].电力系统与控制,2015,43(21):86-92.
[8]阳霜,罗滇生,何洪英,等.基于EMD-LSSVM的光伏发电系统功率预测方法研究[J].太阳能学报,2016,37(6):1387-1395.
[9]徐敏姣,徐青山,袁晓冬.基于改进EMD及Elman算法的短期光伏功率预测研究[J].现代电力,2016,33(3):8-13.
[10]代倩,段善旭,蔡涛,等.基于天气类型识别的光伏系统短期无辐照度发电预测模型研究[J].中国电机工程学报,2011,31(34):28-35.
[11]陈昌松,段善旭,蔡涛,等.基于模糊识别的光伏发电短期预测系统[J].电工技术学报,2011,26(7):83-89.
[12]于秋玲,许长清,李珊,等.基于模糊聚类和支持向量机的短期光伏功率预测[J].电力系统及其自動化学报,2016,28(12):115-118.
[13]YUAN-KANG WU, CHAO-RONG CHEN, HASIMAH ABDUL RAHMAN. A novel hybrid model for short-term forecasting in PV power generation[J]. International Journal of Photoenergy,2014(29):1-9.
[14]郑凌蔚,刘士荣,毛军科,等.一种综合ANFIS和PCA的光伏发电功率预测新方法[J].太阳能学报,2012,33(6):993-1000.
[15]王守相,王亚旻,刘岩,等.基于经验模态分解和ELM神经网络的逐时太阳能辐照量预测[J].电力自动化设备,2014,34(8):7-12.
[16]李乐,刘天琪.基于近邻传播聚类和回声状态网络的光伏预测[J].电力自动化设备,2016,36(7):41-46.
[17]陈红兵,陈希琳,王起,等.冷却肋片对光伏板发电性能的影响研究[J].可再生能源,2015,33(3):346-350.
[18]SUGENO M, KANG G T. Structure identification of fuzzy model[J]. Fuzzy Sets and System,1988,28(1):15-33.
[19]JYH-SHING, ROGER JANG. Anfis: adaptive-network-based fuzzy inference system[J].IEEE Transactions on systems, Man and Cybernetics,1993,23:665-685.
[20]I JAYAWARDENE, G K VENAYAGAMOORTHY. Comparison of adaptive neuro-fuzzy inference systems and echo state networks for PV power prediction[J]. Procedia Computer Science,2015,53:92-102.
[21]李鹏程,陈国华,张力,等.基于ANFIS的人因失误风险严重度识别[J].中国安全科学学报,2014,24(1):72-77.
[22]ALI DEIHIMI, HEMEN SHOWKATI. Application of echo state networks in short-term electric load forecasting[J]. Energy,2012,39(1):327-340.
[23]张晋雁,陶宏才.回声状态网络研究[J].成都信息工程学院学报,2015,30(6):546-550.
(责任编辑:黄健)endprint

