管壳式热交换器扇环形管板开孔应力集中系数分析

， ， ， ，

(河北科技大学 机械工程学院， 河北 石家庄 050018)

管壳式热交换器广泛应用于石油、化工及能源等领域。随着各个行业的快速发展，管壳式热交换器的规模也呈现出大型化的趋势[1-2]，由此导致了热交换器管板直径和厚度的不断增加，使得设计和制造的难度加大。大型管壳式热交换器，如核电工业的蒸汽发生器管板厚度很大，其锻造、钻孔及焊接等都存在许多问题，也会因制造中存在的缺陷而引发一些事故[3-6]。2014年，李海龙[7]对核电蒸汽发生器管板孔桥超差问题进行了分析，结果表明，由于大直径热交换器管板制造困难造成钻孔偏心引起孔桥超差，需要对管板进行改造以保障安全。

针对大直径热交换器管板在设计、制造和应用过程中存在的问题，文中提出了采用分块式扇环形新型组合管板替代整体管板的设计方法，减小了管板的当量尺寸，从而降低了管板厚度和制造难度[8-9]。在总结之前研究成果的基础上，应用ANSYS Workbench分析软件对扇环形管板开孔造成的应力集中情况进行分析[10]，并与未开孔扇环形板的应力分布状况进行对比，得到了扇环形管板开孔应力集中系数，此结果对促进管壳式热交换器设计的技术进步、降低大直径热交换器管板制造难度具有一定意义。

1 扇环形组合管板模型

1.1 组合管板模型

扇环形组合管板是由多个扇环形管板组合而成的一种新型热交换器管板，文中划分为4组管板，见图1。

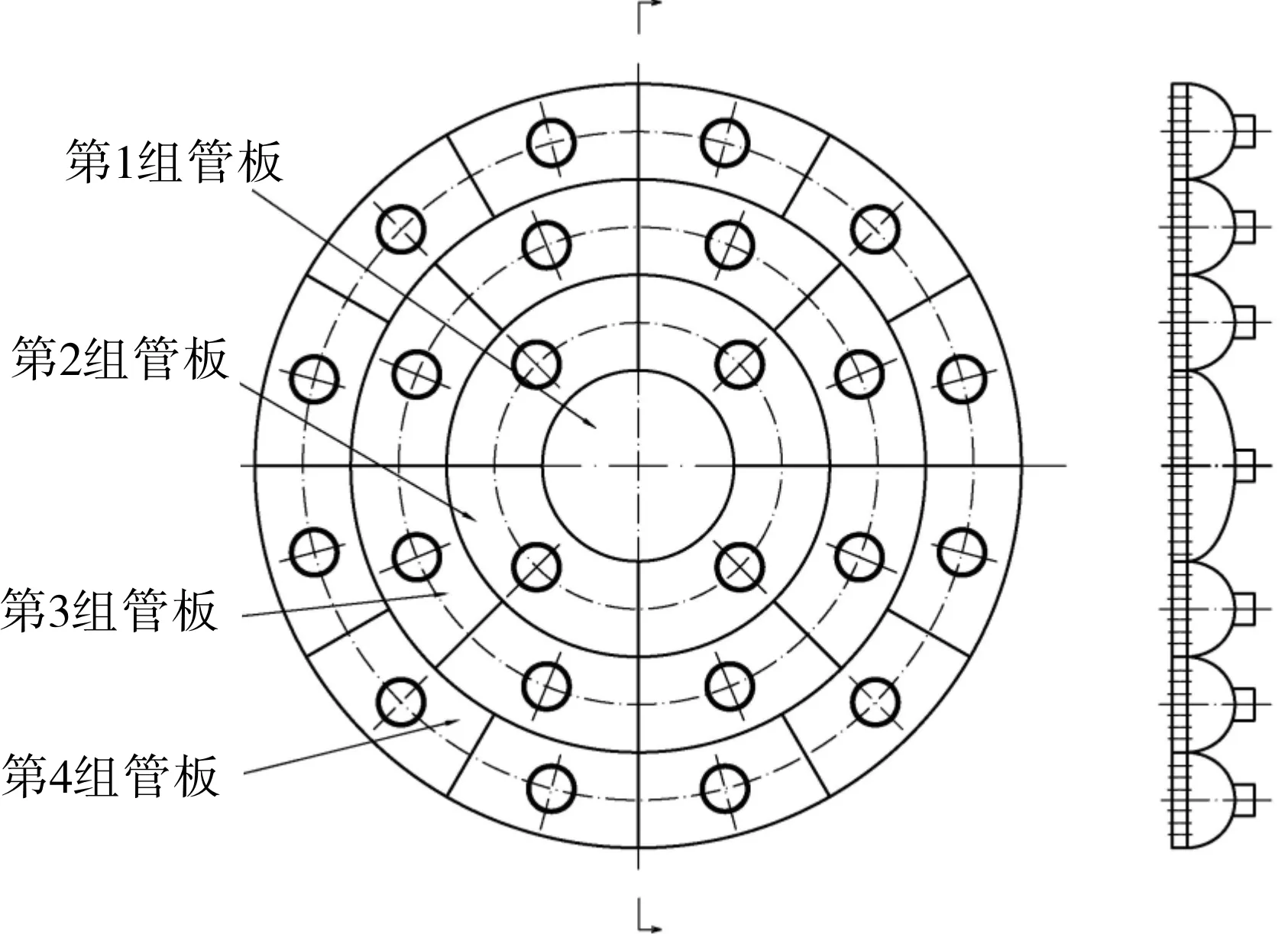
图1 组合管板示图

每个扇环形管板单元由1个扇环形半圆筒、2个半圆端板、1个扇环形管板和1个进口管焊接组合而成，见图2。

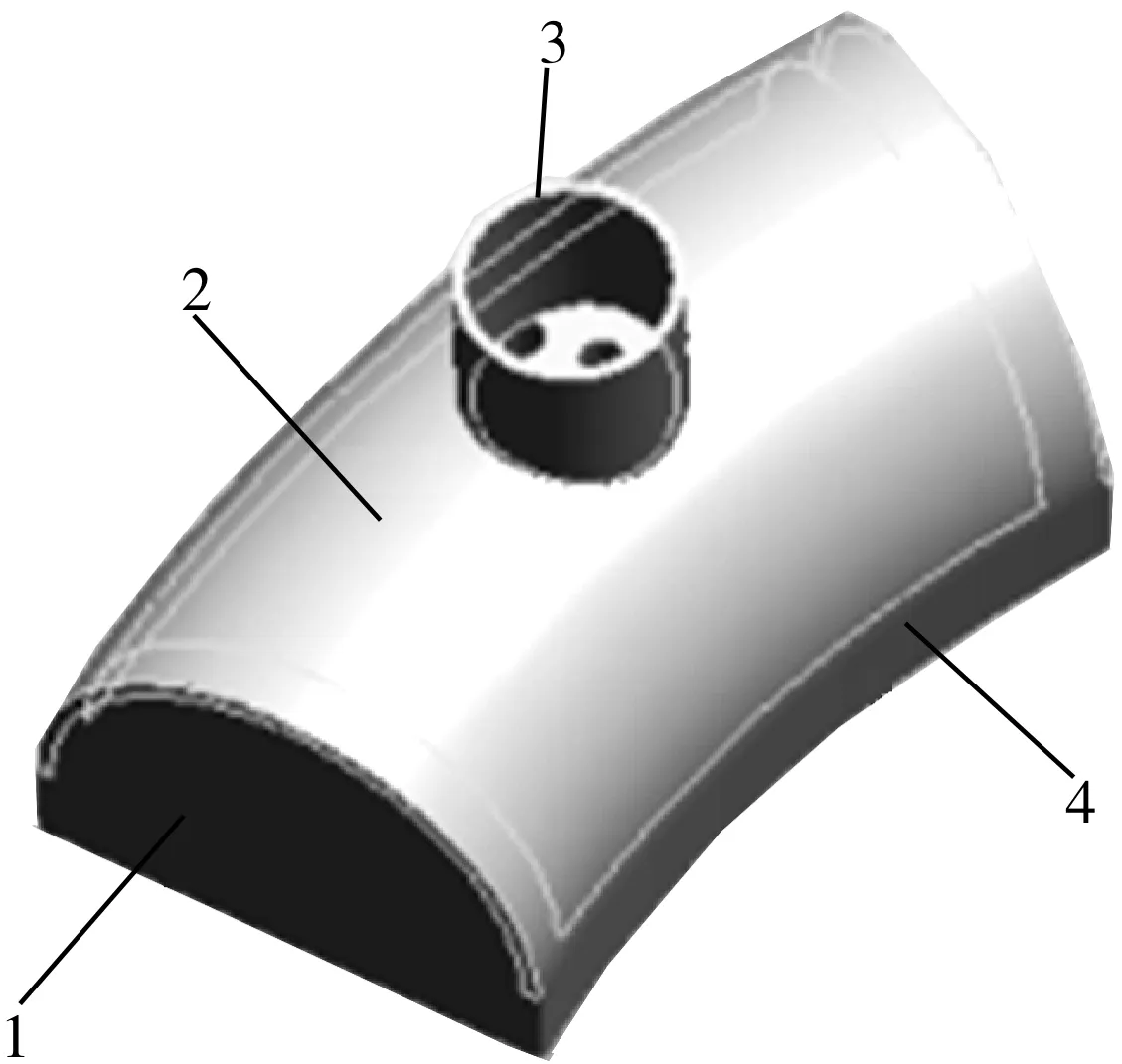
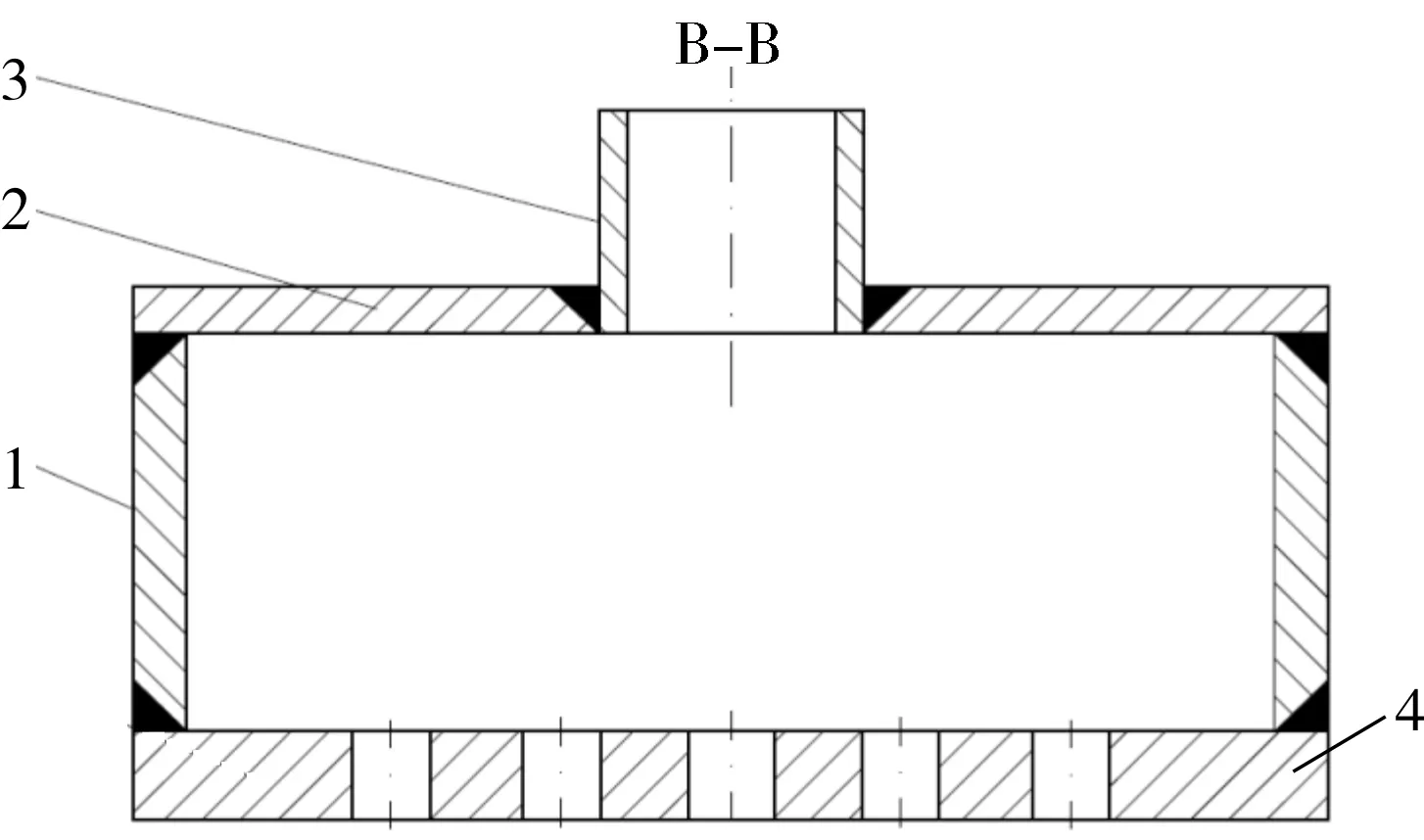
1.半圆端板 2.扇环形半圆筒 3.进口管 4.扇环形管板图2 扇环形管板单元示图

与普通的整体管板相比，扇环形组合管板结构减小了单个管板的当量尺寸，可以有效地减小管板厚度，达到降低设计和制造难度的目的。

1.2 主要参数

设计内压力pi=2 MPa，设计内温度ti取常温，内侧介质为水，设计外压力po取常压，设计外温度to取常温。

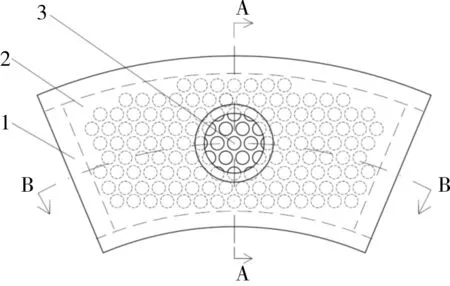
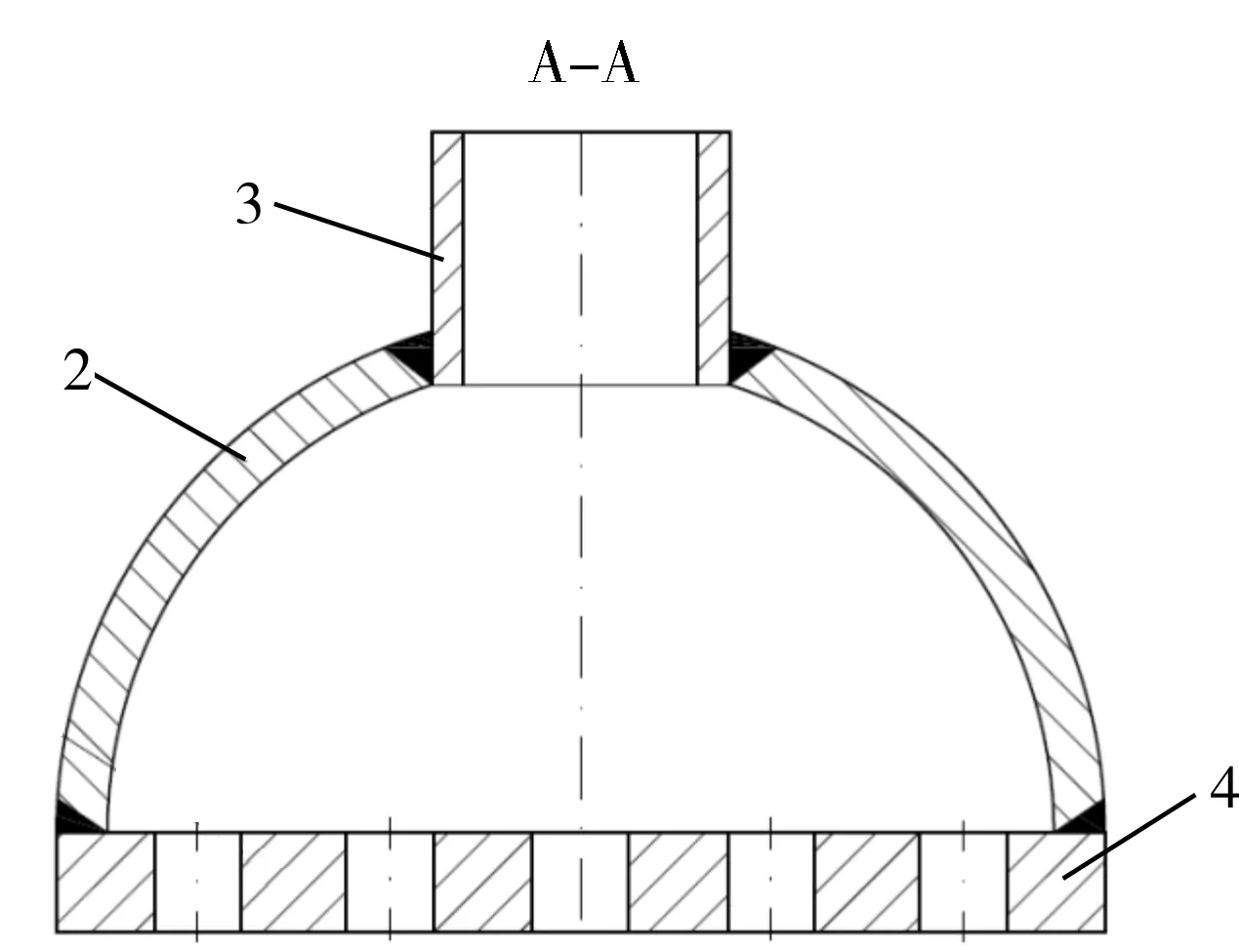
每一个扇环形管板单元都自成一体。在设计过程中，可以针对每一个扇环形管板单元进行独立设计，几何尺寸示意图见图3。图3中，δ1为扇环形管板厚度，R1、R1′分别为扇环形管板内、外半径，R3为扇环形半圆筒半径，δ2为半圆端板厚度，D2为半圆端板直径，δ3为扇环形半圆筒厚度，δ4为进口管壁厚，d4为进口管壁外径，d5为管板孔直径，L5为管板孔间距，mm；θ为扇形角，(°)。

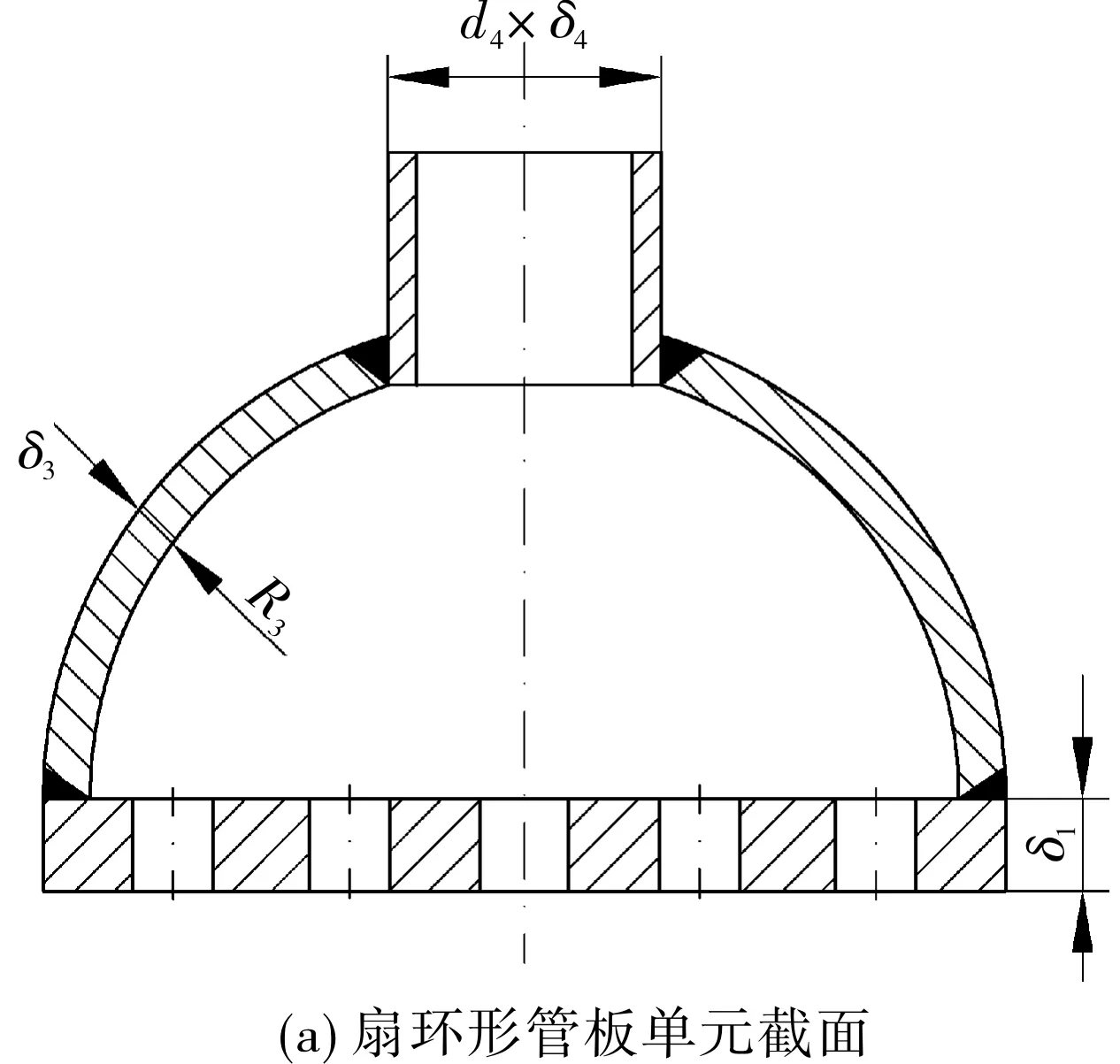
图3 扇环形管板单元几何尺寸示图

1.3 主要零件厚度确定

1.3.1扇环形管板厚度δ1

根据文献[11]的结果，文中取R1=360 mm、R1′=720 mm，则R1/R1′=0.5。

扇环形管板的厚度δ1目前尚无明确的公式可以参考，也是扇环形管板单元设计中的关键部分，一般需要采用应力分析的方法来确定。本文旨在探讨管板开孔造成的孔边应力集中问题，取δ3=60 mm进行分析。

1.3.2半圆端板厚度δ2

δ2可以根据GB 150—2011《压力容器》[12]，按照式(1)计算。

(1)

其中

Z=3.4-2.4a/b

式中，K为结构特征系数，非圆形全焊透结构平盖取0.5；pc为计算压力， [σ]t为材料的许用应力，MPa；φ为焊接接头系数；Z为形状系数；a为非圆形平盖的短轴长度，b为非圆形平盖的长轴长度，mm。

文中示例当中a为半圆端板的半径，即a=0.5D2，长轴b为半圆端板的直径，即b=D2。根据图3b可知：

D2=R1′-R1-2δ3

(2)

由于δ3≪R1，因此忽略δ3的影响，取D2=R1′-R1，则a和b可以按照下式计算。

a=0.5(R1′-R1)

(3)

b=R1′-R1

(4)

根据式(3)和式(4)可知a=180 mm、b=360 mm，带入式(2)计算可得Z=2.2。

将K=0.5、Z=2.2、φ=1.0、[σ]t=120 MPa、pc=2.0 MPa带入式(1)，可以计算得到δ2不应小于24.7 mm。因此，取δ2=25 mm。

1.3.3扇环形半圆筒厚度δ3

δ3可按照圆筒形容器计算[12]，如式(5)所示。

(5)

根据几何关系，R3与半圆端板半径相同，可按照下式计算。

R3=(R1′-R1)/2

(6)

根据式(6)可知R3=180 mm。

许用应力[σ]t、焊接接头系数φ和计算压力pc的取值与半圆端板厚度计算中所取数值一致。将以上参数带入式(5)，可得δ3不应小于3 mm。根据文献[5]的结果，扇环形半圆筒相对圆筒形容器存在一定的应力集中，因此取δ3=10 mm。

1.3.4进口管壁厚

进口管壁厚尺寸取值主要考虑流体流速及流动阻力的影响。本文取进口管直径d4=89 mm、δ4=3.0 mm，并根据式(5)按照圆筒形容器对进口管壁厚进行核算，结果表明此壁厚满足强度要求。

1.4 扇形角θ

以不同扇环形板的扇形角θ(30°、36°、45°、60°、72°)为变量，建立了多组扇环形管板单元模型，其它结构参数：δ1=60 mm、δ2=25 mm、δ3=10 mm、R1=360 mm、R1′=720 mm、pi=2.0 MPa。

管板开孔尺寸d5=25.5 mm，根据GB 151-2014《热交换器》[13]规定，相邻开孔中心的间距L5为1.25倍的开孔尺寸，取L5=32 mm。

2 扇环形管板单元几何建模及有限元网格

2.1 几何模型

采用ProE建立1个扇环形管板单元几何模型，见图4。

图4 1个扇环形管板单元三维模型

由于扇环形管板中心部分应力梯度较大，故对扇环形管板的中间部分网格进行了局部细化。根据网格无关化分析结果，中心区域网格尺寸为2 mm，其余部分扇环形半圆筒、半圆端板和扇环形管板四周部分网格尺寸为8 mm。

以45°扇环形管板单元为例，按此方法对扇环形管板单元划分网格，划分完成后节点数约95万个，单元数约为26万个，见图5和图6。

图5 扇形角为45°时扇环形管板单元模型立体示图

2.2 边界条件及载荷

管壳式热交换器扇环形管板单元的约束和载荷模型见图7。

在扇环形管板单元入口管壁横截面上施加固定约束，所有内表面施加pc=2 MPa的内压，边界条件设置完成后的结果见图8。

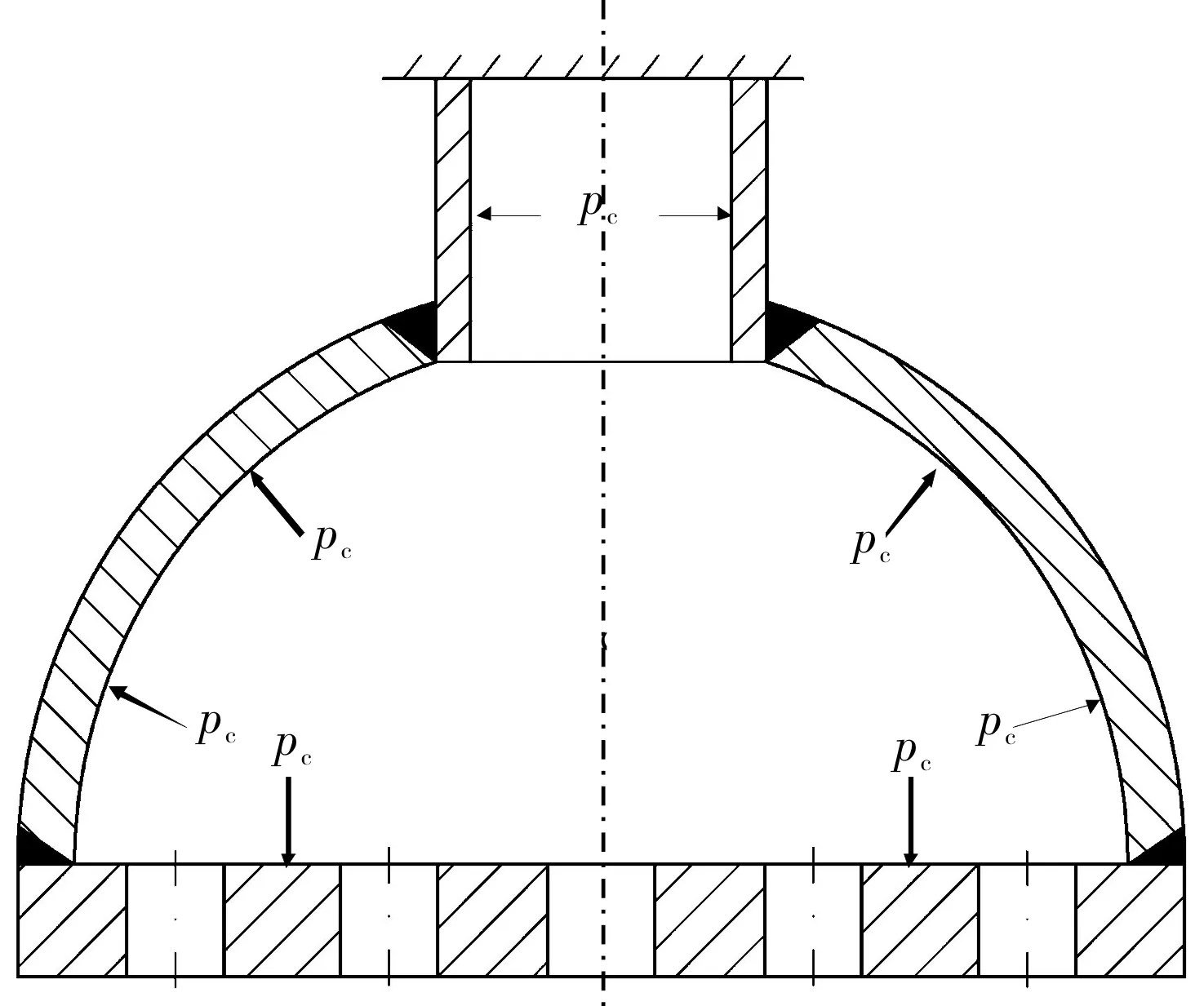
图7 扇环形管板模型约束与载荷

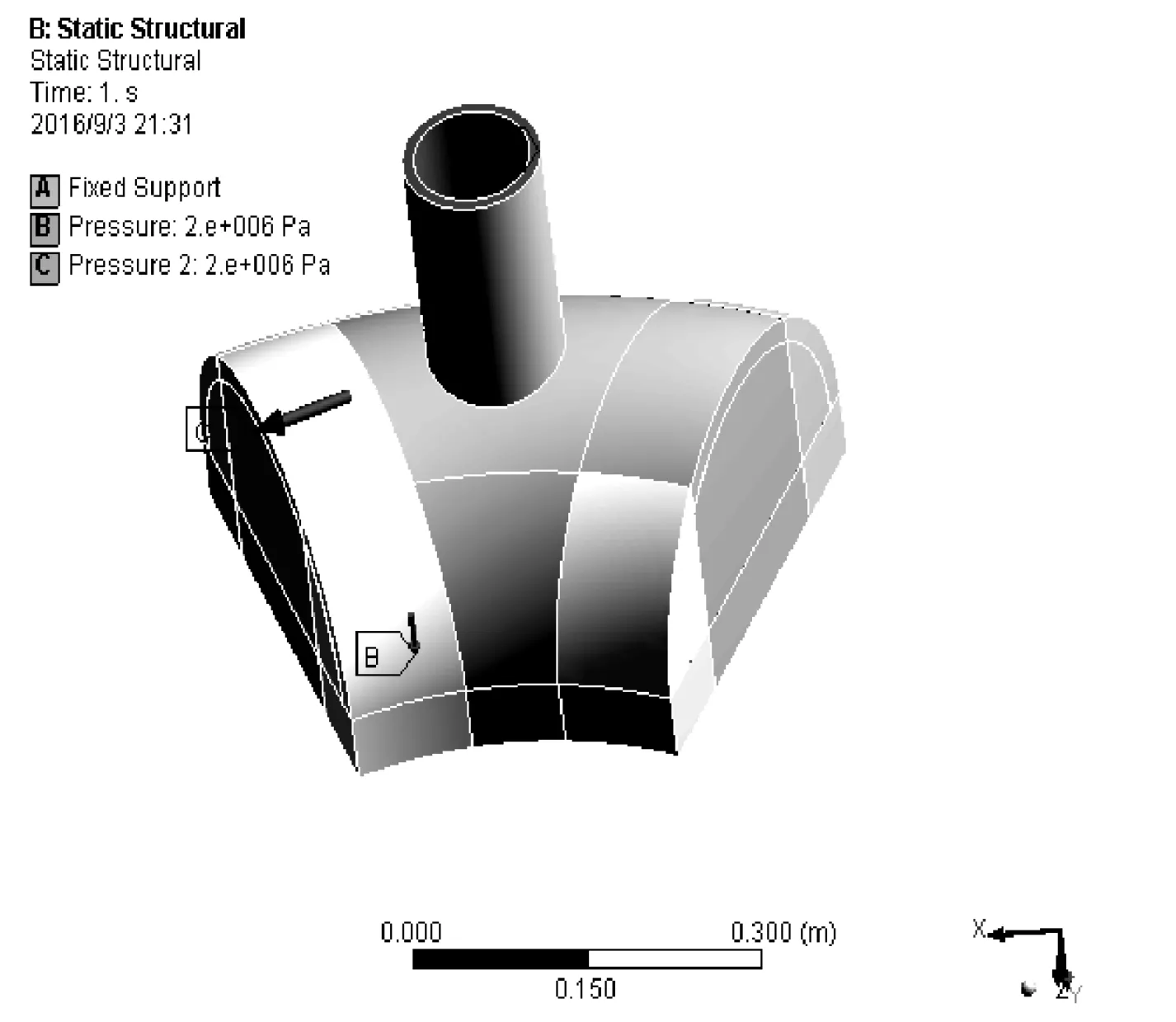
图8 扇环形管板约束条件

3 扇环形管板开孔应力集中系数

在计算开孔造成的应力集中时，需要得到开孔边缘的最大应力值和相同结构不开孔时相同位置的最大应力[14-15]。

应力集中系数的计算方法见式(7)：

(7)

式中，SCF为开孔造成的应力集中系数；(σθ)max为开孔边缘最大应力值，σθm为无开孔相同位置的应力值，MPa。

利用ANSYS Workbench分别对扇形角θ为30°、36°、40°、45°、60°、72°的扇环形管板单元以及相同尺寸、相同约束和载荷条件的扇环形管板(板上未开管孔)两种模型进行数值模拟，得出各自的开孔边缘最大应力值(σθ)max和无开孔时扇环形板管相同位置的应力值σθm，结果见表1。

表1 扇环形管板单元开孔边缘最大应力值和无开孔时相同位置应力值

根据表1中的各个应力集中系数绘制曲线，得到扇环形管板开孔造成的应力集中系数随扇环形管板角度的变化趋势，见图9。

图9 扇环形管板开孔应力集中系数随扇形角变化曲线

从图9中可知，随着θ的增大，开孔造成的应力集中系数先减小后增大，在θ=40°～ 45°时，应力集中系数最小，其数值为1.52。

4 结语

文中提出了一种采用组合扇环形管板替代整体圆形管板的设计新方法。按照此设计方法可以把较大直径的整体管板分成若干扇环形管板单元，由此对每一个扇环形管板单元独立设计。由于降低了管板的当量尺寸，每一个扇环形管板单元中的扇环形管板可以取较小的厚度。在扇环形管板单元设计中，半圆端板和半圆筒可以按照GB 150—2011进行设计，但扇环形管板无法依据标准进行设计，这将是以后课题研究的重点之一。

文中将扇环形管板的扇形角作为设计变量，模拟计算了扇环形管板开孔造成的孔边应力集中系数随扇形角的变化情况。根据计算结果，笔者建议在今后的设计当中，可取θ=40°～ 45°。

[1] 陈永东，陈学东. 我国大型换热器的技术进展[J]. 机械工程学报，2013，49(10): 134-143.

(CHEN Yong-dong, CHEN Xue-dong. Technology Development of Large-scale Heat Exchanger in China[J]. Journal of Mechanical Engineering，2013，49(10): 134-143. )

[2] 杜南麟，陈中灼，陈富彬. 三门核电厂2号机组蒸汽发生器管板钻孔偏差原因分析及问题处理[J]. 核动力工程，2014，35(3):76-79.

(DU Nan-lin, CHEN Zhong-zhuo, CHEN Fu-bin. Disposition of Drilling Deviation for Steam Generator Tube Sheet in Sanmen NPP Unit 2[J]. Nuclear Power Engineering，2014，35(3):76-79. )

[3] 龚代涛，江锋，王欣，等. 秦山第三核电厂核闭式冷却水系统热交换器损坏分析及全面维修[J]. 核动力工程，2017，38(4): 112-115.

(GONG Dai-tao，JIANG Feng，WANG Xin， et al. Failure Analysis and Overall Maintenance of Recirculation Cooling Water System Heat Exchanger of Third Qinshan Nuclear Power Plant[J]. Nuclear Power Engineering，2017，38(4): 112-115. )

[4] 王渝皓，何庆中，王佳，等. 换热器管板堆焊数值模拟及残余应力分析[J]. 现代制造工程，2016(7): 90-94.

(WANG Yu-hao，HE Qing-zhong，WANG Jia，et al. Numerical Simulation of the Heat Exchanger Tube Sheet Welding and Analysis of Residual Stress[J]. Modern Manufacturing Engineering, 2016(7): 90-94.)

[5] 许文镜，刘鸣宇，王小刚. 百万千瓦级核电蒸汽发生器管子-管板焊接工艺研究[J]. 热加工工艺，2012，41(23):170-173.

(XU Wen-jing, LIU Ming-yu, WANG Xiao-gang. Welding Procedure for Tube to Tube Sheet Weld of Million-kilowatt-class Nuclear Power Steam Generator[J]. Hot Working Technology，2012，41(23):170-173.)

[6] 郑张利，吴志远，曹定. AP1000核电厂蒸汽发生器管板堆焊冷裂纹问题分析[J]. 核动力工程，2012，33(5): 120-123.

(ZHENG Zhang-li，WU Zhi-yuan， CAO Ding. Analysis of Cold Crack of AP1000 Steam Generator Tube Sheet Cladding[J]. Nuclear Power Engineering，2012，33(5): 120-123.)

[7] 李海龙，王庆，徐宇，等. 蒸汽发生器管板孔桥超差情况下的结构安全性分析[J]. 原子能科学技术，2014，48(11): 114-118.

(LI Hai-long，WANG Qing，XU Yu， et al. Structural Safety Analysis on Tube Sheet with Deviated Holes in Steam Generator[J]. Atomic Energy Science and Technology, 2014，48(11): 114-118.)

[8] 刘庆刚，王珺，郭彦书，等. 扇环形半圆截面圆筒应力分布规律研究[J]. 河北科技大学学报， 2014，35(4): 66-71.

(LIU Qing-gang，WANG Jun，GUO Yan-shu，et al. Study of the Stress Distribution Principles of an Annular Sector Semicircular Cross Section Vessel[J]. Journal of Hebei University of Science and Technology，2014，35(4): 66-71.)

[9] GARDNER K A. Heat-exchanger Tube-sheet Design[J]. Journal of Applied Mechanics Transactions of the ASMS， 1948，15(4): 377-385.

[10] 宋杨. 海洋平台典型管节点应力集中系数研究[D]. 武汉:华中科技大学， 2012.

(SONG Yang. The Study of Stress Concentration Factor for Some Typical Joints of Offshore Platform[D]. Wuhan: Huazhong University of Science and Technology, 2012.)

[11] 王珺.扇环形半圆截面容器应力分析与设计[D]. 石家庄：河北科技大学，2015.

(WANG Jun. Stress Analysis and Design for Semicircular Cross Section Vessel with an Annular Sector Plate Sheet[D]. Shijiazhuang: Hebei University of Science and Technology，1985.)

[12] GB 150—2011，压力容器[S].

(GB 150—2011，Pressure Vessels[S].)

[13] GB 151—2014，热交换器[S].

(GB 151—2014，Heat Exchanger[S].)

[14] CHANG E，DOVER W D. Stress Concentration Factor Parametric Equations for Tubular X and DT Joints[J]. International Journal of Fatigue，1996，18(6): 363-387.

[15] 彼德森. 应力集中系数[M]. 北京: 国防工业出版社1988.

(Petersen. Stress Concentration Factor[M]. Beijing: National Defense Industry Press，1988.)