基于蚁群优化算法的MR阻尼器模型的参数识别
肖志荣,张正唯
(浙江科技学院 土木与建筑工程学院,杭州 310023)
磁流变(magnetorheological, MR)阻尼器是一种半主动控制装置,由于其出力大、结构形式简单、响应速度快及阻尼力连续可调的特征[1],已经广泛应用于建筑、车辆及桥梁的振动控制中[2-4]。为了能较好地描述MR阻尼器的滞回特性,需要对其模型参数进行识别。但由于MR阻尼器是一种高度非线性的系统,这就给参数识别带来了一定的难度。目前,对MR阻尼器Bouc -Wen模型参数识别的研究有很多。Shen、Jansen等[5-6]认为Bouc -Wen模型中部分参数与电流之间存在一定的函数关系,并利用普通优化算法对模型进行参数识别。但是这种算法在识别多参数变量时的局限性较大,使得最终的识别精度低。Priya、Spencer等[7-10]提出了运用非线性最小二乘法对Bouc -Wen模型中的未知参数进行识别,但是识别精度也不高。本研究运用的蚁群优化算法是一种自组织算法,它主要采用正反馈调节机制保证算法能够不断收敛,强化了种群中的优良个体,同时信息素的不断挥发也增加了种群的多样性,因此蚁群优化算法具有全局寻优能力和鲁棒性强等特点。目前,该算法用于一些模型和参数区间反问题等参数优化[11-13]。由于蚁群优化算法中有多种参数变量,其组合影响着模型识别的精确程度,因此,本研究通过对网格划分蚁群算法的参数逐个分析,找到参数的最佳组合,从而提高模型参数的识别精度。
1 Bouc -Wen模型
为了描述MR阻尼器在低速阶段的力与位移之间的关系, Wen[14]提出了Bouc -Wen模型。相对于其他力学模型,Bouc -Wen模型能够较好地拟合出MR阻尼器的滞回特性,同时参数个数也相对较少,便于程序化。Bouc -Wen滞回模型的数学表达式为:
(1)
(2)
式(1)~(2)中:c0为黏滞阻尼系数;k0为刚度系数;x0为初始位移偏差;α为屈服前后的刚度之比;z为滞回变量;γ、β、A为由磁流变液和控制系统决定的模型参数。
本研究选择Bouc -Wen模型中的参数作为MR阻尼器模型参数识别的对象。
2 基于网格划分策略的连续域蚁群算法
2.1 算法步骤
基于网格划分策略的连续域蚁群算法是解决连续域优化问题的蚁群算法之一,算法主要的实现步骤[15]如下:
1)初步估算各变量的取值范围,Xjl≤Xj≤Xju(j=1,2,3,…,n)。其中Xjl、Xju分别是Xj的最小值和最大值。
2) 将各变量的取值范围分成N等分,每个节点之间的距离为
(3)
3)当max(h1,h2,h3,…,hn)<ε时,则算法停止,其中ε为网格划分粗细程度。此时算法最优解为
(4)
否则将会继续进行下一步。
4) 当循环次数Ni=0时,给每节点上的初始信息素τij赋相同的值,并设置蚂蚁数量m、信息素总量Q、挥发系数η及最大循环次数Nmax的初始值。
5) 对每只蚂蚁按状态转移公式(5)选择下一节点
(5)
6)按照更新方程(6)修改每次循环过程中的信息素,其中f是所求的目标函数值。
(6)
7)此时,循环次数将变为Ni+1。如果Ni+1 (7) 返回到第2步,其中参数μ的取值范围一般设为[1,6]。 固定的磁流变液,n值是固定的[16]。为简化识别过程,本文取n=2。此时,Bouc -Wen模型中的未知参数还剩下7个,即γ、β、A、c0、k0、x0、α。同时根据文献[17]的数据及Bouc -Wen模型参数值,将Bouc -Wen的参数取值放大,设为0≤γ≤50、0≤β≤50、50≤A≤100、50≤c0≤300、0≤k0≤50、0≤x0≤50、1 000≤α≤20 000。 在识别过程中,通过构造目标函数来确定算法中的更新方程。目标函数表达式如下: (8) 式(8)中:n为数据采集的个数;Fi为通过蚁群优化算法仿真出的第i个阻尼力;Fti为采集数据中的第i个阻尼力;R为采集数据中最大阻尼力与最小阻尼力之间的差值。 图1 蚂蚁数量与目标函数的关系Fig.1 Relationship between ant number and objective function 图2 信息素与目标函数的关系Fig.2 Relationship between pheromones and objective function 在基于网格划分策略的蚁群算法中,需要确定的参数主要有蚂蚁数量m、等分区间N、总信息量Q、挥发系数η及区间变化参数μ。本文中参数的最佳取值范围是通过固定其中4个参数的值,改变1个参数的数值,来进行数值分析。其中参数Nmax、μ的取值参考了文献[18]参数选取原则。各参数的取值范围分别如下:最大迭代Nmax=50,精度ε=1e-4,m的范围为[0,150],N的范围为[0,100],Q的范围为[0,100],η的范围为[0.1,0.9],μ的范围为[1,6]。 由于其他电压下蚁群算法中参数的分析与10 V时类似,故本研究主要以10 V为对象对参数进行分析。参数与目标函数值的柱状图见图1~4。 蚂蚁数量m的大小与解的个数有关,1只蚂蚁循环1次就是1个解的产生。这就意味着随着蚂蚁个数的增多,解的个数就会越多。从算法的角度而言,即加强了算法的全局搜索能力,算法的随机性增加。而蚂蚁个数较少时,虽然收敛速度提高,迭代次数降低,但是算法很容易搜索到局部最优值或其他的可行解。从图1可以看出,当蚂蚁数量较少时,目标函数值相对比较大;当蚂蚁数量为110只左右时,目标函数达到最优,说明一定数量上的蚂蚁是有效优化的保证。从区间[130,150]中发现,当蚂蚁数量过多时,被搜索路径上的信息素较多,信息素的正反馈调节不够明显,反而可能会导致目标值的升高。同时,所需的优化时间也相对较多。 参数Q是蚂蚁在循环1次所留下的信息素总量。随着循环次数的增加,信息素总量也会继续叠加,从而加强了蚁群算法的正反馈调节机制。可见参数Q的选择是影响着算法的收敛速度以及是否能够达到最优解的因素。从图2仿真结果可以看出,当总信息量在区间[10,50]上时,目标函数值相对于其他情况优化结果较好。原因在于当总信息素较大时,正反馈调节起主导作用,多数蚂蚁会向当前最优解移动,可能会出现蚂蚁搜索到相同解的现象,使搜索到的解范围变小,导致算法趋向局部最优。 图3 挥发系数与目标函数的关系Fig.3 Relationship between volatilization coefficient and objective function 参数η是信息素的挥发系数。蚂蚁在路径上循环1次时,会在路径上残留部分信息素,此部分残留的信息素会指导下一次循环中蚂蚁的行为。假设参数η较大时,即残留的信息素较小,这种情况会使得算法很难收敛,从而使得迭代次数增加。相反,参数η较小时,蚂蚁在路径中易陷入局部最优。从图3仿真结果可以看出,挥发系数处于0.1时,目标函数值处于较低的水平。 参数N、μ是连续域网格划分蚁群算法中所特有的。参数N是划分区间的重要参数,N过于小时,所划分的网格较为粗略,有可能导致遗漏全局最优解。N较大时,使得迭代次数增加,优化过程较长。同样,参数μ的意义与参数N相近。在1次循环的最终,需要对变量进行范围的缩小。参数μ范围的大小,影响着下一次蚂蚁搜索的区间。区间太小,也可能会舍去一些最优解。从图4仿真结果可以看出,参数N为 90等分左右时,目标函数值较优,说明等分区间一定程度的细化能够使搜索精度提高。对参数μ而言,一般取较小值能使得目标函数值达到较优,说明增大下一次循环的搜索范围,可使搜索全局最优解的概率提高,更容易得到最优解。 图4 N和μ与目标函数的关系Fig.4 Relationship between N, μ and objective function 电压/Vm/只QηNμ0110100.17015140100.110110110100.110315120100.480120110100.1901 按照上述方法对参数进行逐个分析,得出了蚁群优化算法的最优参数取值区间。同时将不同电压下蚁群算法中各参数的最优值组合成该电压下的最优参数组合,如表1所示。由表1可以看出,这些参数的最优组合基本上处于上述参数的取值区间内。 在上述得到的各电压下蚁群算法的最优参数组合的基础上,对Bouc -Wen模型进行识别,不同电压下参数的识别值及目标函数值如表2所示。 表2 Bouc -Wen模型参数识别值及目标函数值Table 2 Parameter identification values of Bouc -Wen model and objective function value 由表2可知,不同电压下识别的目标函数值均维持在1e-5数量级左右,误差相对较小。同时,为了更易于查看参数随电压变化的关系,根据上述电压及电压为3、13 V下各参数的取值,作出如图5所示的变化趋势图。 图5 参数随电压变化的趋势Fig.5 Tendency of parameters changing over voltage 从图5中可知,参数γ、β、A、k0、x0随着电压U的增大而随机变化,而参数c0、α基本上随着电压U的增大有规律地变化。因此,对参数γ、β、A、k0、x0取平均值,分别为γ=30.42 cm-2、β=32.03 cm-2、A=61.53、k0=15.59 N/cm、x0=16.45 cm。对于参数c0、α,采用origin中的拟合命令进行多项式拟合,拟合曲线如图6所示。拟合结果中R2分别为0.950 41、0.964 93,接近于1,说明拟合结果满足要求。拟合出的表达式见式(9)。 c0=92.51+14.72U-0.42U2,α=2 181.47+1 389.06U-38.17U2。 (9) 根据上述各参数的结果,采用识别值与真实值的相对误差来判断基于网格划分的蚁群优化算法识别的精度。相对误差如表3所示,其中相对误差的计算公式为: (10) 式(10)中:δ为相对误差;x为估计值;L为真实值。 图6 参数拟合曲线Fig.6 Fitting curve of parameter 参数识别值真实值相对误差/%c0a/[(N·s)·cm-1]92.5182.612.00c0b/[(N·s)·(cm·V)-1]14.7214.32.93c0c/[(N·s)·(cm·V2)-1]-0.42-0.3520.00k0/(N·cm-1)15.591055.90x0/cm16.4518.611.56α0a/(N·cm-1)2181.472331.46.43α0b/[N·(cm·V)-1]1389.061290.47.65α0c/[N·(cm·V2)-1]-38.17-32.816.37γ/cm-230.42301.40β/cm-232.03306.77A61.53602.55 由表3可知,除参数k0的相对误差较大外,其余所识别的参数值与真实值的相对误差均较小,可见,识别精度较高。同时,采用优化后的参数,绘制阻尼力与时间、位移及速度的数据与仿真值的对比图(图7)。 图7 数据与仿真值对比Fig.7 Comparison between data and simulation 仿真结果表明:从整体上来看,曲线数据与仿真值吻合度较高,说明参数k0对实际的曲线精度并无太大的影响;同时,可以看出蚁群优化算法能够对多变量参数模型进行有效的识别,并且识别精度较高。上述分析表明基于网格划分的蚁群算法对Bouc -Wen模型参数识别的可行性。 本研究首先选择了Bouc -Wen模型作为MR阻尼器的力学模型,通过基于网格划分策略的蚁群算法对Bouc -Wen模型进行了参数识别,并对在参数识别过程中蚁群优化算法的参数进行了讨论。结果表明: 1) 蚁群优化算法中蚂蚁数量、总信息量等参数之间的组合对Bouc -Wen模型的识别效果影响较大,故确定这些参数组合至关重要。 2) 蚁群优化算法能够较好地对Bouc -Wen模型中的参数进行识别,拟合结果吻合,识别精度较高。因此可以将该算法推广到其他MR阻尼器模型的参数识别中。 [1] 欧进萍. 结构振动控制:主动、半主动和智能控制[M]. 北京:科学出版社,2003. [2] 于国军, 杜成斌, 万发学. 高耗能自解耦式MR阻尼器的设计及性能试验[J]. 振动、测试与诊断,2012,32(3):426. [3] 廖英英, 刘永强, 杨绍普, 等. 磁流变阻尼器逆向模型的建模、优化与仿真[J]. 振动、测试与诊断,2013,33(4):701. [4] 付志强. MR阻尼器逆模型实现梁桥半主动减震研究[D].北京:北京交通大学,2016. [5] SHEN Y, GOLNARAGHI M F, HEPPLER G R. Load-leveling suspension system with a magnetorheological damper[J]. Vehicle System Dynamics,2007,45(4):297. [6] JANSEN L M, DYKE S J. Semi-active control strategies for MR dampers: a comparative study[J]. Journal of Engineering Mechanics,2000,126(8):795. [7] PRIYA C B, GOPALAKRISHNAN N. Parameter identification of long stroke and short stroke MR damper for its use in semi-active vibration control[J]. Journal of the Institution of Engineering,2016,97(4):405. [8] SPENCER Jr B F, DYKE S J, SAIN M K, et al. Phenomenological model of a magnetorheological damper[J]. Journal of Engineering Mechanics,1997,123(3):230. [9] YANG G Q, SPENCER Jr B F, JUNG H J, et al. Dynamic modelling of large-scale magnetorheological damper systems for civil engineering applications[J]. Journal of Engineering Mechanics, ASCE,2004,130(9):1107. [10] JUNG H J, SPENCER Jr B F, LEE I W. Control of seismically excited cable-stayed bridge employing magnetorheological fluid damper[J]. Journal of Structural Engineering,2003,129(7):873. [11] 朱林. 基于蚁群算法的参考天空分类优化方法研究[D]. 重庆: 重庆大学,2012. [12] 郭红玲, 杨海天, 赵潇. 蚁群算法求解弹性本构参数区间反问题[J]. 工程力学,2012,29(1):7. [13] 侯景伟, 孔云峰, 孙九林. 蚁群算法在需水预测模型参数优化中的应用[J]. 计算机应用,2012,32(10):2952. [14] WEN Y K. Method of random vibration of hysteretic system[J]. Journal of Engineering Mechanics Division,1976,102(2):249. [15] 高尚, 钟娟, 莫述军. 连续优化问题的蚁群算法研究[J].微机发展,2003,13(1):21. [16] 刘永强, 杨绍普, 廖英英, 等. 基于遗传算法的磁流变阻尼器Bouc -Wen模型参数辨识[J]. 振动与冲击,2011,30(7):263. [17] 徐龙河. 基于MR阻尼器的半主动结构控制的理论与试验研究[D]. 天津: 天津大学,2003. [18] 黄永青, 郝国生, 钟志水,等.基于网格划分策略的连续域改进蚁群算法[J].计算机工程与应用,2013, 49(9):61.2.2 模型参数取值的规定
3 参数分析
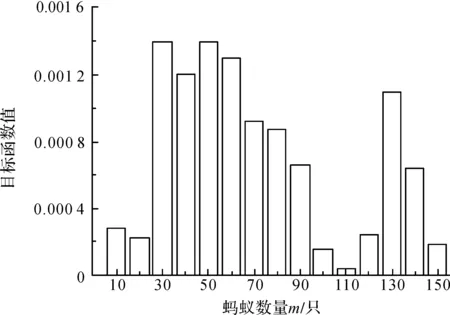

3.1 蚂蚁数量m
3.2 信息素总量Q
3.3 挥发系数η

3.4 参数N和μ


3.5 不同电压下蚁群算法参数的最优组合
4 算例分析





5 结 论

