ReLU激活函数优化研究*
蒋昂波,王维维
(浙江大学 超大规模集成电路设计研究所,浙江 杭州310027)
0 引 言
长短期记忆模型[1](long short term memory,LSTM)作为递归神经网络(recursive neural network,RNN)非常重要的一个改进,能够有效记忆和利用历史信息,已经在文本分析、语音识别、图像处理等众多领域得到了成功应用,极大促进了深度学习领域的发展。但其结构的复杂性导致训练模型的过程比较耗时。本文采用Cho K在2014年提出的门控循环单元[2](gated recurrent unit,GRU)结构,是一种在结构上改动比较大的LSTM变体,其将LSTM结构中的遗忘门(forget gate)和输入门(input gate)合并成一个更新门(update gate),使得深度神经网络在运算的候少了很多矩阵乘法,从而改善了LSTM训练耗时的缺点,在数据量很大的情况下,GRU能节省更多的时间。
激活函数是GRU等深度神经网络结构的核心所在,目前常见的激活函数包括sigmoid[3]系的sigmoid和tanh函数,ReLU系的ReLU[4],LReLU函数等。但sigmoid系的函数在后向传递的过程中出现了梯度消失[5](gradient vani-shing)问题,极大地降低了训练速度。
ReLU函数能够有效缓解梯度消失问题,其以监督的方式训练深度神经网络,无需依赖无监督的逐层预训练,显著提升了深度神经网络的性能。Krizhevsky A[6]等人对常用的激活函数ReLU,sigmoid和tanh函数进行了测试,证明了ReLU函数的性能优于sigmoid系函数。
但ReLU也存在着致命的缺点。首先,ReLU函数的输出大于0,使得输出不是0均值,即均值偏移[7](bias shift),易导致后一层的神经元得到上一层输出的非0均值的信号作为输入,使得网络参数W计算困难。其次,随着训练的推进,部分输入会落入ReLU函数的硬饱和区,导致对应权重无法更新。均值偏移和神经元死亡共同影响了深度神经网络的收敛性和收敛速度。
本文在GRU结构上对sigmoid系的激活函数和ReLU系的激活函数进行了对比和研究,详细分析了两类激活函数存在的优缺点,并在此基础上设计了一种新的激活函数双曲正切线性单元(tanh linear unit,TLU),其综合了sigmoid系和ReLU系函数的优点,既能有效缓解梯度消失问题,也有效地避免了均值偏移现象。实验证明:这种新的函数在提升神经网络训练速度和降低误差率方面的作用非常显著。
1 激活函数的对比与研究
1.1 sigmoid系激活函数
sigmoid系函数包括sigmoid和tanh。sigmoid函数定义为
(1)
其函数图像如图1所示。
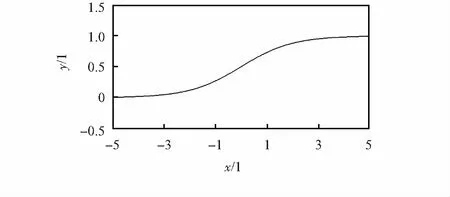
图1 sigmoid函数
从函数表达式和图像可见,sigmoid函数具有软饱和性[8]:在定义域内处处可导,当输入非常大或非常小时,其图像的斜率趋近于0,即导数逐渐趋近于0。这种性质导致了梯度消失现象,使得深度神经网络一直难以得到有效训练,是阻碍神经网络发展的重要原因。
具体地,深度神经网络在使用梯度下降算法求解网络参数W时,在后向传递过程中,sigmoid函数向下传导的梯度包含了一个自身关于输入的导数f'(x),当输入落入饱和区时,f'(x)的值趋近于0,导致向底层网络传递的梯度变得非常小,使网络参数W很难得到有效训练。
sigmoid函数也存在均值偏移的缺点,从函数图像可以看出,sigmoid函数的值域为{∀x,y=f(x)≥0)},则其输出均值必然非负,导致了sigmoid函数在训练一些超深网络时会出现训练结果不收敛的问题。
tanh函数是sigmoid函数的一个变体,缓解了sigmoid函数所遇到的均值偏移问题,定义为
(2)
其图像如图2所示。
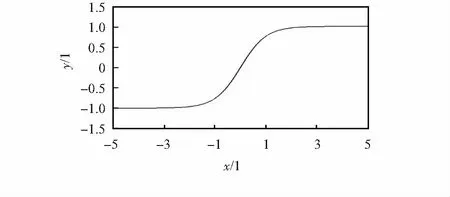
图2 tanh函数
从图像以及函数表达式中可以看出,tanh函数也具有软饱和性,因此,也存在梯度消失的缺点。但其值域为[-1, 1],因此,输出均值趋近于0,缓解了均值偏移问题,使得随机梯度下降(stochastic gradient descent,SGD)更接近自然梯度(natrual gradient),从而降低了计算网络参数 所需的迭代次数,提高了深度神经网络的训练速度。
1.2 ReLU系激活函数
ReLU函数有效解决了sigmoid系函数的梯度消失问题,但依然存在均值偏移的缺点。定义为
f(x)=max(0,x)
(3)
其函数图像如图3所示。

图3 ReLU函数
从函数表达式和图像可知,当x≥0时,其导数为1,因此,ReLU函数能够在x≥0时保持梯度不衰减,可以有效地缓解梯度消失问题。
当x<0时硬饱和[8]。如果有输入落入此区域,则该神经元的梯度将永远为0,不会再对任何数据有激活作用,即神经元死亡,直接导致计算结果不收敛。而且,ReLU函数在x<0时输出为0,使得整体输出均值大于0,无法缓解均值偏移问题。
PReLU函数为ReLU函数的改进版本,具有非饱和性,能够缓解均值偏移问题和神经元死亡问题,其定义为
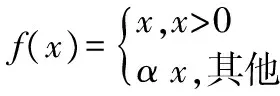
(4)
其函数图像如图4所示。其中x<0部分的图像根据其斜率α变化,一般α=0.25。

图4 PReLU函数
与ReLU函数相比,PReLU函数中的负半轴斜率系数α可以学习而非固定,输出均值趋近于0,而且x<0时函数非硬饱和,因此,PReLU函数的收敛速度更快,无神经元死亡的问题。
另外,其他激活函数如RReLU,ELU等亦能够提高收敛速度。
2 改进的ReLU激活函数TLU
对ReLU函数进行了改进,将ReLU函数x<0的部分使用tanh函数代替,构造出了一个新的激活函数TLU,函数定义为

(5)
其图像如图5,其中,x<0部分图像根据斜率α变化。
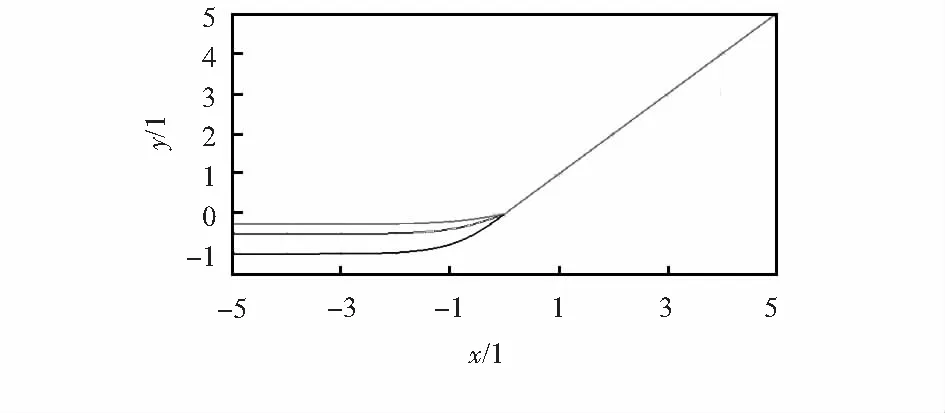
图5 TLU函数
从函数表达式和图像中可以看出,TLU在右侧的线性部分具有函数ReLU和LReLU的优点,在x≥0时导数为常数,因此,在饱和区内的梯度永远不会为0,能够有效缓解梯度消失问题。
1)TLU函数与ReLU函数对比,左侧的非线性部分(x<0部分)不仅能够使得均值更接近于0,避免均值偏移现象,而且由于其左侧部分不具备硬饱和的性质,TLU不会出现神经元死亡现象。
2)虽然LReLU函数在x<0部分也能取值从而使均值趋近于0,但LReLU函数左侧部分是线性的,对输入变化或噪声的鲁棒性较弱,而TLU函数左侧部分是非线性的具有软饱和性,鲁棒性更好,因此,可以预测TLU函数的性能必然强于LReLU函数。
3 实验与结果分析
采用字符集语言模型,在GRU型的深度网络结构进行实验。实验环境为Ubuntu15.04LTS,Torch7,LuaRocks以及使用 NVIDIA推出的通用并行计算架构CUDA Toolkit的NVIDIA GPU。训练数据集是部分Linux Ubuntu源代码,约5 MB。
由于使用sigmoid激活函数进行实验时出现了结果不收敛的情况,所以实验结果仅使用了同为sigmoid系的tanh函数作为对照组,另外还增加了一个ELU激活函数作为对照组。使用不同的激活函数的GRU型深度神经网络的训练结果如图6所示,实验结果表明:在相同的训练时间下,误差率从低到高排序依次为TLU 图6 实验结果 另一方面,在同等误差率下,按照训练时间从小到大排序依次为TLU 设计了一种新的激活函数TLU,并与一些sigmoid系和ReLU系的激活函数进行了比较,实验证明:TLU能显著地加快深度神经网络的训练速度并有效地降低训练误差。实验表明,TLU的系数α对训练时间和误差有一定的影响,下一步研究工作将对参数α进行优化,以进一步提高TLU函数的性能。 [1] Gers F.Long short-term memory in recurrent neural network-s[D].Hannover,Germany:Universität Hannover,2001. [2] Cho K,Van Merri⊇nboer B,Gulcehre C,et al.Learning phrase representations using RNN encoder-decoder for statistical machine translation[J].arXiv preprint arXiv:2014,1406.1078. [3] 李宏伟,吴庆祥.智能传感器中神经网络激活函数的实现方案[J].传感器与微系统,2014,33(1):46-48. [4] Nair V, Hinton G E. Rectified linear units improve restricted Boltzmann machines[C]∥Proceedings of the 27th International Conference on Machine Learning(ICML),2010:807-814. [5] Hochreiter S.The vanishing gradient problem during learning recurrent neural nets and problem solutions[J].International Journal of Uncertainty,Fuzziness and Knowledge-Based Systems,1998,6(2):107-116. [6] Krizhevsky A,Sutskever I,Hinton G E.Imagenet classification with deep convolutional neural networks[C]∥Neural Information Processing System,2012:1097-1105. [7] Clevert D E,Unterthiner T,Hochreiter S.Fast and accurate deep network learning by exponential linear units(elus)[J].arXiv preprint arXiv:2015,1511.07289. [8] Gulcehre C,Moczulski M,Denil M,et al.Noisy activation functions[J].arXiv preprint arXiv:2016,1603.00391. [9] He K,Zhang X,Ren S,et al.Delving deep into rectifiers: Surpassing human-level performance on imagenet classification[Z].2015:1026-1034.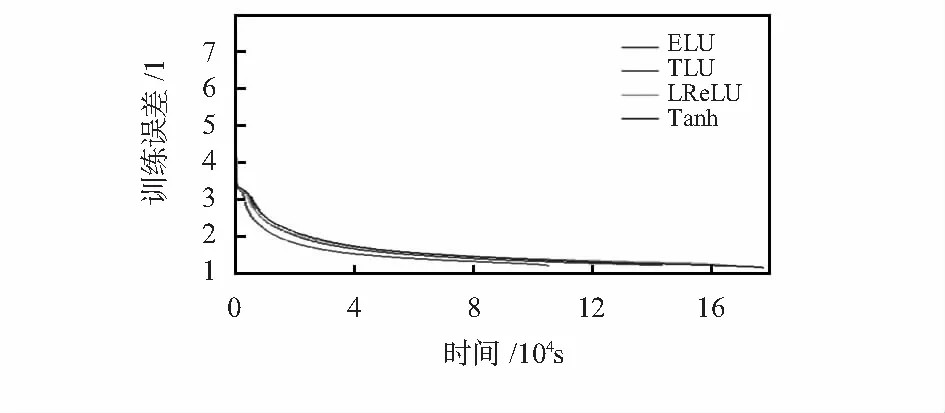
4 结束语

