例谈高中物理核心素养下科学思维能力的培养*

曾 斌

(广东实验中学 广东 广州 510375)

习题教学一直是高中物理教学中的重要方面，尤其是在高三复习教学中.但在当前复习课中存在这样的困局：教师被内容知识复习而劳累，学生被考试成绩低下而困惑，双方都付出了很多的心血，但总不能达到理想的效果.究其原因，最核心的欠缺就是在教学中忽视了对科学思维能力的培养[1].

我们现在正进行新一轮基础教育课程改革，而在此轮课程改革中，发展学生的“核心素养”是现阶段课程改革和教学改革的主要方向[2].物理学科的核心素养中，让学生形成科学思维是很重要的一个要素，也是当前高考中的热点与重点问题.在科学思维能力的建构中，多种思维方法的训练与提升将变得越来越重要.那么高三复习教学中有哪些核心的思维方法最值得我们去注意总结？在教学中如何加以总结与提升？笔者结合多年来的教学实践，认为可以侧重于下面几种思维方法的培养，现将这些思维方法总结出来供大家参考.

1 等效法

等效法亦称“等效替代法”，是科学研究中常用的思维方法之一.掌握等效方法及应用，体会物理等效思想的内涵至关重要.等效思想和方法作为一种迅速解决物理问题的有效手段，经常体现于高考命题中.等效方法是在保证某种效果(特性和关系)相同的前提下，将实际的、复杂的物理问题和物理过程转化为等效的、简单的、易于研究的物理问题和物理过程来研究和处理的方法.

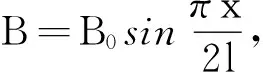
(1)回路产生的热量；

(2)通过左端电阻R的电荷量.

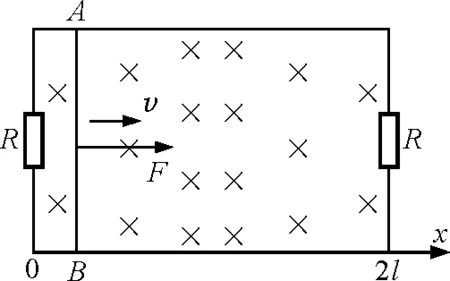
图1 例1题图

思维方法：(1)导体棒在向右匀速运动过程中，产生的感应电动势为

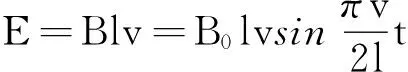
这个表达式与学过的交流电的表达式完全相似，所以整个过程就等效于交流电产生的瞬时电动势，那么根据交流电知识可得以下公式

Em=B0lv

以上公式求得回路产生的热量为

(2)如果直接求通过电阻的电荷量，从现有的高中知识是求不出来的.但如果换个角度，将题设过程与“面积为S的线圈，在磁感应强度为B0的匀强磁场中，从垂直于磁场方向的初始位置起以角速度ω匀速转动半圈”相类比，并以此等效代换题设过程，如表1所示,于是便可得相应的量

Em=B0lv=B0ωSΦm=B0S

以上公式最终求得通过左端电阻R的电荷量为

表1 题设过程与等效过程类比

方法小结：本题将一个比较陌生的过程用我们熟悉的模型进行等效代换，从而对相关问题作出快捷的解答.这正是“等效法”在解题时的优势所在.

等效法在解决电场、磁场、重力场等复合场时显得尤其方便，也是常用的方法之一，需要大家熟练运用.那么运用等效法处理问题的思路一般可归纳为：

(1)分析原事物(需研究求解的物理问题)的本质特性和非本质特性；

(2)寻找适当的替代物(熟悉的事物)，以保留原事物的本质特性，抛弃非本质特性；

(3)研究替代物的特性及规律；

(4)将替代物的规律迁移到原事物中去；

(5)利用替代物遵循的规律、方法求解，得出结论.

2 极限法

将某些物理量的数值推向极值(如设动摩擦因数趋近零或无穷大、电源内阻趋近零或无穷大、物体的质量趋近零或无穷大、斜面的倾角趋于0°或90°等)，并根据一些显而易见的结果、结论或熟悉的物理现象进行分析和推理的一种方法.

【例2】如图2所示，一半径为R的绝缘环上，均匀地带电荷量为Q的电荷，在垂直于圆环平面的对称轴上有一点P，它与环心O的距离OP=L.静电力常量为k，关于P点的场强E，下列4个表达式中有一个是正确的，请你根据所学的物理知识，通过一定的分析，判断正确的表达式是( )

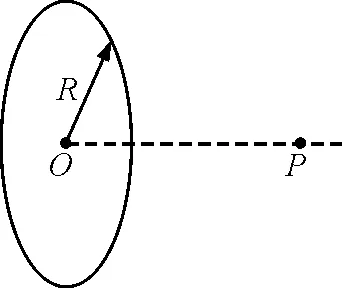
图2 例2题图

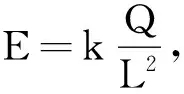
方法小结：有的问题可能不容易直接求解，但是当将题中某物理量的数值推向极限时，就可以对这些问题的选项是否合理进行分析和判断.这种方法在解决选择题时显得很快捷.

3 对称法

对称情况存在于各种物理现象和物理规律中，应用这种对称性可以帮助我们直接抓住问题的实质，避免复杂的数学演算和推导，这样能快速解决问题.

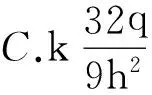
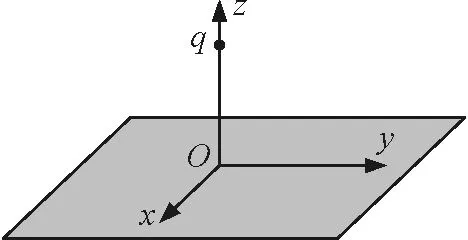
图3 例3题图

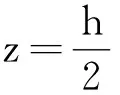
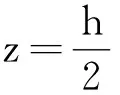
正确选项为D.

方法小结：对称法在解决电场叠加时尤其有用.根据对称性，经常将面电荷或线电荷的场强转化为点电荷的场强.

对称法指图形或物体相对的两边的各部分,在大小、形状和排列上具有一一对应的关系，这里更多的是指物理过程和规律的对称关系.如镜像对称、时间对称、空间对称等.一般来说有下列过程：

(1)领会物理情境，选取研究对象.在仔细审题的基础上，通过题目的条件、背景、设问，深刻剖析物理现象及过程，建立清晰的物理情境，选取恰当的研究对象,如运动的物体、运动的某一过程或某一状态.

(2)透析研究对象的属性、运动特点及规律.

(3)寻找研究对象的对称性特点，在已有经验的基础上通过直觉思维，或借助对称原理的启发进行联想类比，来分析挖掘研究对象在某些属性上的对称性特点.这是解题的关键环节.

(4)利用对称性特点，依物理规律求解.

第二、三两种方法在解决选择题时尤其能体现出时间上的优势，特别是针对全国卷计算题量大，模型建立比较复杂时，大家不妨运用这两种方法可以起到意想不到的效果.

4 微元法

微元法做为一种数学方法，在物理思维上有很重要的应用.近几年高考的命题实践来看，涉及到“微元法”的试题出现很多.“微元法”在被应用于物理解题时，常可以把题中给出的变化的事物或题中反映的变化的过程转化为极为简单而不变的事物或不变的过程来处理.由于一切“变化”都必须在一定的时间和空间范围内才能得以实现，“微元法”就是通过限制“变化”所需的时间或空间来把变化的事物或变化的过程转化为不变的事物或不变的过程.

【例4】如图4所示，正方形闭合导线框以速度v1在光滑绝缘水平面上匀速运动，穿过有理想边界的匀强磁场区域后以速度v2做匀速直线运动，则当完全处在磁场区域内时的运动速度u为( )

D.无法确定

图4 例4题图

思维分析：设导线框在“穿入”或“穿出”磁场的过程中某一瞬间速度和加速度分别为v和a，则由相应的物理规律依次可得

E=LvBE=IR

FB=ILB-FB=ma

由此可得v和a间的瞬时关系为

此式中，导线框的质量m,边长L,电阻R以及磁场的磁感应强度B均为常量，而导线框在“穿入”或“穿出”磁场过程中某一瞬间的速度v和加速度a均为变量.

因此，选用具备“化变为恒”功能的“微元法”进行分析.其具体分析步骤依次如下：

(1)取“时间微元Δt”同乘以上式两端，为

(2)考虑到“速度v和加速度a均为变量”而不具备“平权性”特征，所以应实施“换元”的相关操作.

(3)考虑到尽管“速度v和加速度a均为变量”，但由于“Δt→0”，所以在趋近于零的“时间微元Δt”内可将“速度v”和“加速度a”均视为“不变”(事实上是“来不及变”)而顺利实施“换元”，即在

Δx=vΔtΔv=aΔt

的关系代入后上式变为

(4)考虑到此式中对应于微元Δx和Δv的“权函数”分别为

f2(v)=m=k2=常量

而满足所谓的“平权性”特征，所以分别在导线框“穿入”和“穿出”的过程中对上式实施相应的“叠加”操作，即“穿入”时有

“穿出”时有

(注：设当导线框刚要“穿入”磁场时其位置坐标为x=0，磁场区域的宽度为b)

(5)由此“叠加”分别可得

(6)联立上述两式最终解得

所以此例选B.

再举一例来强化微元法.

【例5】(2016年高考全国Ⅰ卷第35题)某游乐园入口旁有一喷泉，喷出的水柱将一质量为M的卡通玩具稳定地悬停在空中.为计算方便起见，假设水柱从横截面积为S的喷口持续以速度v0竖直向上喷出；玩具底部为平板(面积略大于S)；水柱冲击到玩具底板后，在竖直方向水的速度变为零，在水平方向朝四周均匀散开.忽略空气阻力.已知水的密度为ρ，重力加速度大小为g，求：

(1)喷泉单位时间内喷出的水的质量；

(2)玩具在空中悬停时，其底面相对于喷口的高度.

思维分析：(1)在一段很短的Δt时间内，可以认为喷泉喷出的水柱保持速度v0不变.

该时间内，喷出水柱高度

Δl=v0Δt

(1)

微元法可得喷出水柱质量

Δm=ρΔV

(2)

其中ΔV为水柱体积，满足

ΔV=ΔlS

(3)

由式(1)、(2)、(3)可得喷泉单位时间内喷出的水的质量为

(2)设玩具底面相对于喷口的高度为h,如图5所示，由玩具受力平衡得

F冲=Mg

(4)

其中，F冲为水体对玩具底部的作用力．

由牛顿第三定律

F压=F冲

(5)

其中，F压为玩具底部下表面对水体的作用力.设v′为水体到达玩具底部时的速度,由运动学公式得

(6)

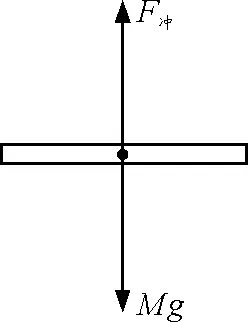
图5 例5题图

设在很短Δt时间内，冲击玩具水柱的质量为Δm，则

Δm=ρv0SΔt

(7)

由题意可知，在竖直方向上，对该部分水柱,由动量定理

(F压+Δmg)Δt=Δmv′

(8)

由于Δt很小，Δmg也很小，可以忽略，式(8)变为

F压Δt=Δmv′

(9)

由式(4)、(5)、(6)、(7)、(9)可得

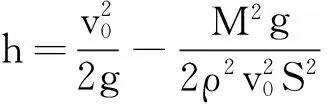
方法小结：微元法思维步骤一般分以下3步.(1)选取元；(2)运用规律表达元；(3)叠加元求解全过程.中学阶段，“微元法”的换元类型主要包括 “时间元”与“空间元”间的相互代换、 “体元”“面元”与“线元”间的相互代换、 “线元”与“角元”间的相互代换.

本文通过对上面4种思维方法的总结，为学生的物理核心素养的养成提供了素材，让学生掌握提高科学思维能力的一般方法.如果我们在平时教学中注重这些物理模型与科学思维的建立，那么一定会为学生的终身发展提供无限的动力.当然，物理思维方法还不止于本文总结.在解决物理问题时这些思想方法的确非常重要，期待在以后的教学中能更加深化与应用.

1 曾斌.浅谈高中物理复习教学如何构建高效课堂.物理通报,2016(11):4～6

2 侯海军,孙明西.基于物理核心素养的高中物理教学探讨.物理教学探讨,2016 (10):39～40