公共自行车复杂网络可达性指标潜力评价模型*
吕 铃,彭雅丽,曾欣怡,杨雨鑫,黄明和
(江西师范大学软件学院,江西 南昌 330022)
1 引言
近年来,公共自行车已经成为人们生活中必不可少的一项基础设施,在城市的发展中起着重要的作用。但是,随着使用人数的增多,规模的扩大,其在实际运营中出现了一些管理运营方面的共性问题,如由于其网点布设不合理造成在高峰时段无车可借、低峰时段车辆使用率较低、车辆调度不合理、车辆损坏严重、无人维修等情况,严重制约着公共自行车的正常运转和进一步发展。因此,对公共自行车系统布局的合理性和运营情况进行综合评价,筛选出问题节点,及时进行管理控制,进而可以为公共自行车网点的布设、车辆投放力度提供科学合理的依据。
复杂网络近年来吸引了广大交通学者的目光,人们针对公交、地铁、航空、铁路等行业进行网络建模和数据分析。高自友等人[1]利用复杂网络、动力学分析等理论,探索了城市交通网络的时空复杂性及演化机理。Borgnat等人[2]提出将自行车网点作为节点,自行车的共享交换为连边,构建复杂网络,研究人们出行的动力学统计特性在时空分布中的特点。郑啸等人[3]以北京市公交为例,对网络的基本拓扑特性和关键节点进行分析,为城市交通规划提供了参考意见。邓羽等人[4]通过可达性与道路密度双重指标的运用进行区域综合分区,揭示了北京市城区内的空间可达性特征和道路基础设施建设情况以及两者在南北城区内的空间表征差异。刘志林、王茂军[5]基于问卷数据,测度了北京城市124个街道的就业可达性,并将其作为职住空间错位的标度指标,讨论了职住空间错位与居民通勤时间之间的关系。陈靖[6]提出了一种以时间符号迁移图为建模语言,基于可达性分析的模型检测算法。文献[7]认为目前评价节点重要性的方法比较单一,进而提出了一种考虑了多种因素的节点重要性评价方法。尚焱等人[8]在筛选关键节点时将用户系数和传播系数作为微博传播网络的节点和边的权重,形成双向加权网络,从而评估网络中节点的重要程度。周漩等人[9]综合考虑了节点效率、节点度值和相邻节点的重要度,提出了一种利用重要度矩阵来评价网络关键节点的方法。文献[10]提出了一种基于TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)的新复杂网络节点重要性的评估方法。文献[11]围绕城市环境信号衰减、红灯等停、固定和周期的公交运行模式,提出分层分区的通信模型,以解决城市交通问题。可见,通过构建复杂网络能对交通网络的整体拓扑进行精准的分析,对其网络关键节点进行合理的筛选,为交通规划提供理论依据。公共自行车因其交通功能的特殊衔接性,若能结合其中短距离出行和长距离出行进行不同的功能分析,必能得出更有意义的系统建设方案。
本文基于公共自行车基础运营数据,通过分析复杂网络拓扑特性,同时引入针对用户出行目的和出行距离为基础的分区可达性指标和网络容量潜力分析模型,从技术因素方面分析网络的内部结构和功能,筛选出网络的关键节点。本文将该方法与传统的基于度数和介数筛选关键节点的方法进行了比较分析,对现有公共自行车系统的运营情况进行了综合评价,对网点的建设和车辆投放力度提供参考意见,以最大限度地发挥系统效益。
2 公共自行车复杂网络的构建
2.1 公共自行车系统基本数据
本文研究所使用的数据来自于某市公共自行车运营系统记录的用户出行数据,数据包括434个自行车租赁网点和2016年7月~2016年12月5个月的用户出行数据。由于所获取的数据是该市公共自行车系统的硬件设备上传的数据,系统有时会发生设备断电和断网的情况,导致部分数据丢失;同时,由于有人工调度的干预,和人们日常使用检查车辆的问题,有很多测试或无效数据,需要进行简单的预处理。我们的预处理主要包括:
(1)将借还车间隔时间在1 min以内、大于1 440 min(24小时)的借还数据删除。1 min内的借还数据,可推测为查车数据;而大于1 440 min的数据认为是自行车被盗、维修数据或非正常借还数据,因此,去除这两类数据。
(2)对于出现故障的网点进行筛选,删除故障网点。
2.2 基于用户借还的网络模型构建方式
根据以上系统记录的用户出行基础数据,本文利用复杂网络的基本理论进行数据建模。在模型中,以Δtk时段内的所有用户产生的借还量为数据进行建模,借还涉及到的网点为网络节点,记为V;单次借还数据关联的两个网点间建立连边,记为E;连边方向为借出网点流入归还网点,每产生一条借还记录该方向上的边权加1。公共自行车网点既有流出量,又有流入量,因此该网络是一个加权有向网络。给每个节点id进行唯一编号i,其容量定义为ci,并定义由idi→idj的总流量为wij。由此可以产生一个由点集V和边集E组成的图G,可以表示为G=(V,E),图的权重为总流量wij。节点vi的度ki指的是与其直接相连的边的数量。在有向图中,节点的度可以分为入度和出度,入度指的是流入该节点的边的数量;出度指的是从该节点流出的边的数量;度指的是与节点vi连接的边的总数。
最终构建的复杂网络模型有节点434个,边19 472条,整个网络的模型如图1所示。图中的点代表网络的节点,点之间的连线代表网络的边。

Figure 1 A complex network model of public bicycles in a city图1 某市公共自行车复杂网络模型示意图
3 公共自行车复杂网络拓扑性质分析
3.1 无标度特性
王姣娥等人在文献[12]中提出,当累积度分布为幂函数时,称其结构具有“无标度”性质,同时提到具有小世界特性的网络含有大的集聚系数和小的平均路径长度。
我们计算入度累积度分布图,在双对数坐标下利用线性回归得到方程y=0.6217-0.00007616x,回归系数R2=0.7259,说明公共自行车复杂网络入度累积度分布符合幂律分布,结果如图2a所示。
计算出度累积度分布图,在双对数坐标下利用线性回归得到方程y=0.6341-0.00007957x,回归系数R2=0.7384,说明公共自行车复杂网络出度累积度分布符合幂律分布,结果如图2b所示。
计算平均聚类系数值为0.63,存在74.7%的网点聚类系数大于0.5,表现出了较强的聚集性,说明网络中各节点与其邻居之间的联系紧密,这也比较符合公共自行车的实际运营模式。同时,计算得到网络平均路径长度为3.052,网络直径为6。综合以上指标,表明该市公共自行车网络具有小世界无标度特性,且符合“6度空间理论”。

Figure 2 Weighted cumulative distribution图2 加权累积度分布图
3.2 网络分布分析
对于公共自行车复杂网络上的任意节点,节点的入度表示该节点的直接流入量,即车辆的还入量;出度表示该节点的流出量,反映的是该节点的车辆借出量。根据半年的交易数据,计算网络中节点的入度值和出度值,发现不同网点的使用次数存在着极大的差距。判定这种差异是否与节点的实际地理位置或其所处的功能区域等因素相关,还需根据其坐标、功能分区等做进一步分析。表1给出了公共自行车复杂网络度值分布表。从表1中可以看出,仅有19.12%的节点日平均借出量和归还量在20次以上,表明网络中节点分布相对不均匀,仅有少部分节点的度值较高被频繁使用,这部分节点是网络的关键节点,与其它节点连通性好,处于人流量大的枢纽位置,在网络中发挥着极其重要的位置,同时这部分网点最有可能出现失衡现象。所以,如何筛选出这部分关键节点,对其进行控制,对于优化整个网络具有重要的意义。因此,本文提出了一种基于出行目的和出行距离的分区可达性指标来选取关键节点的方法。
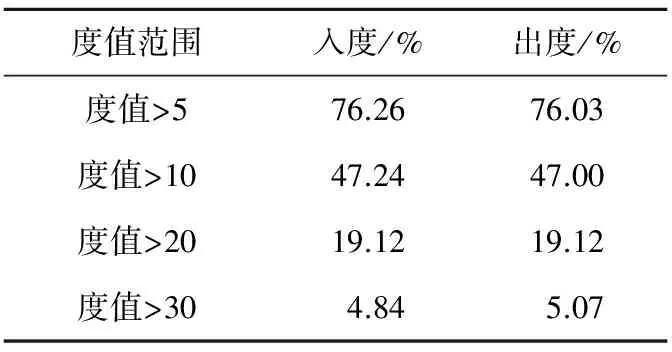
Table 1 Degree distribution of thepublic bicycles complex network
4 网络可达性指标及潜力评价模型
4.1 网络划分和可达性概念
公共自行车慢行交通的发展,一方面可以直接承载人们的短距离出行需求,另一方面能完成轨道+公交的“最后一公里”接驳,实现长距离出行的公共交通衔接。而要提高公共自行车在公共交通中的衔接作用,增强城市公共交通的竞争力最有效的措施就是通过各种办法来改善其可达性。因此,准确、合理、全方位地分析城市公共自行车慢行交通的可达性,并针对不足之处进行改善,提高公共自行车的运行效率,对促进公共交通发展,缓解交通拥堵,减少环境污染具有重要意义。
因此,公共自行车系统评价,不仅需要挖掘复杂网络的拓扑特征,还应分析公共自行车作为一种公共交通工具所承担的交通可达性功能。首先将节点地域按照功能属性进行划分,紧扣公共自行车的公共交通特性,划分为中短距离出行和长距离公共交通衔接区域,并通过可达性评价指标和潜力模型对整体网络进行交通功能的综合评估,具体如图3所示。
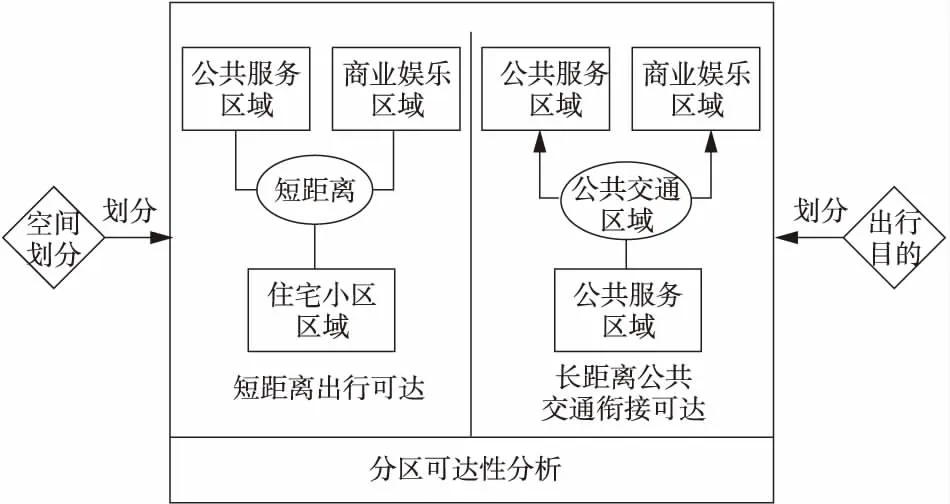
Figure 3 Network division method图3 网络划分方法
4.1.1 网络划分
公共自行车作为现有公共交通的合理补充,其主要功能是承载人们的中短距离出行需求并在长距离中实现和公共交通的衔接,紧扣这个公共交通核心功能,我们拟将节点数量庞大、出行复杂、功能繁多的公共自行车交通网络,进行功能属性的划分,将各网络节点所在的区域,及其在网络中的地位、关系展现出来。具体的划分算法分三步:
(1)节点功能区域划分。
结合人们出行需求中的目的地功能,将所有的节点进行功能区域划分,主要有公共交通区域、住宅区域、公共服务区域和商业娱乐区域。公共交通区域主要包括城市内主要的公交站点、地铁站点;住宅区域主要包括人们的住宅小区;公共服务区域主要包括人们日常公共服务的场所,例如学校、银行、医院、行政服务点等;商业娱乐区域主要包括超市、购物中心、娱乐场所、景点休闲场所等。
(2)系统核心功能划分。
为完成长距离公共交通衔接核心功能,公共自行车的每一个数据流都必然有一个属于公共交通区域,因此,划分为以公共交通为核心,与住宅、公共服务、商业娱乐三大分区的长距离公共交通衔接可达,这是一个公共交通衔接区域。
为完成中短距离出行,划分住宅、公共服务、商业娱乐三大分区的中短距离出行区域,这类区域需将进一步划分。
(3)中短距离出行区域划分。
中短距离出行必须进一步根据距离和节点分布划分成若干个中短距离范围内的住宅区域、公共服务区域和商业娱乐区域,这样一个完整的短距离范围就是我们要寻找的中短距离区域。中短距离区域划分算法:第一步,以人们的住宅小区为基点,所有该小区可达的节点都划分进该区域内;第二步,若两个相邻的小区,与其他三个区域内的度相关性分布相似,则将两个区域合并;循环进行度相关性判断,直至所有区域划分完成。
划分完成后具有一个公共交通衔接区域和多个中短距离出行区域,我们主要研究区域内部节点之间的可达性,通过可达性评价指标判别节点属性。
4.1.2 可达性指标
交通的本质是人们因为某种目的而发生的空间位移,是为了能够便利地到达目的地,因此,国内外专家认为可达性是交通的根本目的。在已有的各种公共交通系统中,公路、铁路、地铁、公交都提出采用可达性分析作为评价交通系统的重要指标。因此,引入可达性指标作为公共自行车系统节点的一个重要属性指标。
可达性的评价模型中,空间相互作用模型定义可达性为空间相互作用的潜力,认为可达性不仅与两点间的空间阻隔有关,还与起点或终点活动规模的大小有关。Hansen提出的潜力模型就是空间相互作用模型的代表,其基本形式如下:
(1)
其中,Ai是节点i的可达性,即节点i与当前连接的所有其它节点相互作用过程中可能获得的全部机会,dij是节点i和节点j之间的距离,a是反映距离阻抗影响程度的参数,Dj是节点j中的机会。
节点所划分的区域中,如果该节点处于中短距离出行中的某个区域,则需计算生活小区网点到商业娱乐、公共服务类型的综合可达性。若处于长距离公共交通衔接区,则在公共交通区域的该节点,需要计算交通枢纽类网点与生活小区、公共服务、商业娱乐的综合可达性;节点的可达性指标值越高,说明该节点处于该功能区的中心,会承担更多的用户流量,是网络中的关键节点。
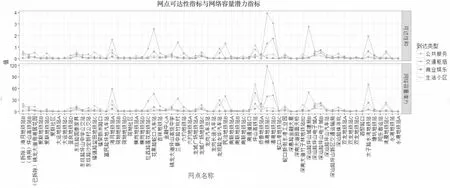
Figure 4 Potential index and the reachability index of the node from the transport hub type network reach to the transport hub,public service,living area and commercial entertainment type network图4 交通枢纽-交通枢纽、公共服务、生活小区、商业娱乐可达性指标与网络容量潜力指标
4.1.3 容量潜力模型
一个网点的容量潜力用Ei表示,其基本形式如下:
Ei=Ai*Ci
(2)
其中,Ci为每个节点的容量,Ai为节点可达性指标。
相对潜力用Di表示,其基本形式如下:
(3)
将节点可达性指标与网点容量潜力相关联,对分析网络的潜力需求具有重要的指导意义。
4.2 长距离公共交通衔接区域可达性分析
长距离公共交通衔接区域到达各功能区域的可达性值可以通过计算其到达该类型内所有网点可达性值的和来表示。计算过程中反映距离阻抗影响程度的参数取1。图4a和图4b分别表示了该市公共自行车网络中64个交通枢纽类网点到交通枢纽、生活小区、公共服务、商业娱乐类型网点的可达性值和网络容量潜力指标。两图横坐标均表示网点名称,纵坐标分别表示每个网点每天每公里可达性指标和网点容量潜力。从图4中可以看出,同一网点到达不同功能类型区域的可达性指标存在较大差异,这表明不同网点由于其所处的地理位置不同,会导致其衔接的功能区有所不同;并且从交通枢纽出发,到达生活小区和公共服务两类网点比较便捷;且不管目的地是何种类型网点,长距离出行的衔接主要是通过少部分节点实现的,表明这少部分网点在交通枢纽功能区内处于核心,承担着主要的出行流量,这部分网点可以被判定为网络的关键节点。针对网点容量潜力的分析同样可以看出,网络中存在少部分节点网络潜力相对较高,一个网点的容量潜力值越大,表明该网点所处的区域条件越好,越重要,到其它网点越便捷。对于网络潜力较高的点,要和实际的流量进行分析比较,根据结果,若实际流量也是最高的,那可以增设网点,若实际流量不算高,说明该网点可能因为调度不及时或初始容量设置不高,导致其巨大的潜力未能展示出来,应重点调整调度方案和初始布设。
分析结果显示,交通枢纽与生活小区、公共服务、商业娱乐衔接性的好坏可以通过网点容量的相互潜力来评价。计算结果显示交通枢纽到生活小区、公共服务、交通枢纽、商业娱乐类型网点的相对网点容量潜力分别为0.20,0.52,0.15,0.12。这个结果表明从交通枢纽到公共服务和生活小区类型网点的相对发展潜力较好。针对这种情况,可依据实际流量值,着重关注交通枢纽与生活小区、生活服务交易的调度。
4.3 中短距离衔接区域可达性分析
中短距离出行必须进一步根据距离和节点分布划分成若干个中短距离范围内的住宅区域、公共服务区域和商业娱乐区域,这样一个完整的短距离范围就是我们要寻找的中短距离区域。首先,我们筛选出所有生活小区类网点;然后计算出任意两个节点之间的距离,绘制距离累积分布图,如图5所示,横坐标表示生活小区距离分布图,纵坐标表示累积分布。从图5中可以看出,生活小区类网点的布设相差范围在0~30 000 m,结合实际生活场景,我们暂时将距离5 000 m以内的生活小区类网点划分至同一区域,已经被划分的生活小区类网点将不再出现在另一个划分区域中,循环进行,直至所有的生活小区类网点划分完毕,并将可以到达该生活小区区域的网点划分进该区域内,最终我们得到了5个区域。区域划分结果如表2所示。

Figure 5 Distance accumulation distribution map of the living community图5 生活小区距离累积分布图

区域网点总数生活小区类型网点数目交通枢纽类型网点数目公共服务类型网点数目商业娱乐类型网点数目区域18836122812区域29510204916区域399157689区域416039335731区域5682492015
为了计算中短距离区域的交通可达性,针对5个区域的数据做如下处理:删除网点功能属性为交通枢纽类型的用户出行数据。然后对5个区域分别计算生活小区-商业娱乐、生活小区-公共服务、生活小区-生活小区的可达性指标和网络容量潜力。结果如图6和图7所示。
从对比图形结果可以得出,在中短距离衔接的区域内,从生活小区出发到生活小区和商业娱乐的可达性值会出现特别高的网点,即在个别网点存在大量的用户选择公共自行车去商业中心和休闲娱乐场所,针对这部分网点,可以适当增设锁车柱,增大车辆的投放力度或在其周边也可以适当增设网点。对比长距离衔接和中短距离衔接区域的可达性,可以发现两种方式流量的疏通主要都是通过少部分节点实现的,这部分节点即该网络中的关键节点。中短距离衔接区域中生活小区类型网点到生活小区、商业娱乐和公共服务类型的相对容量潜力如表3所示。
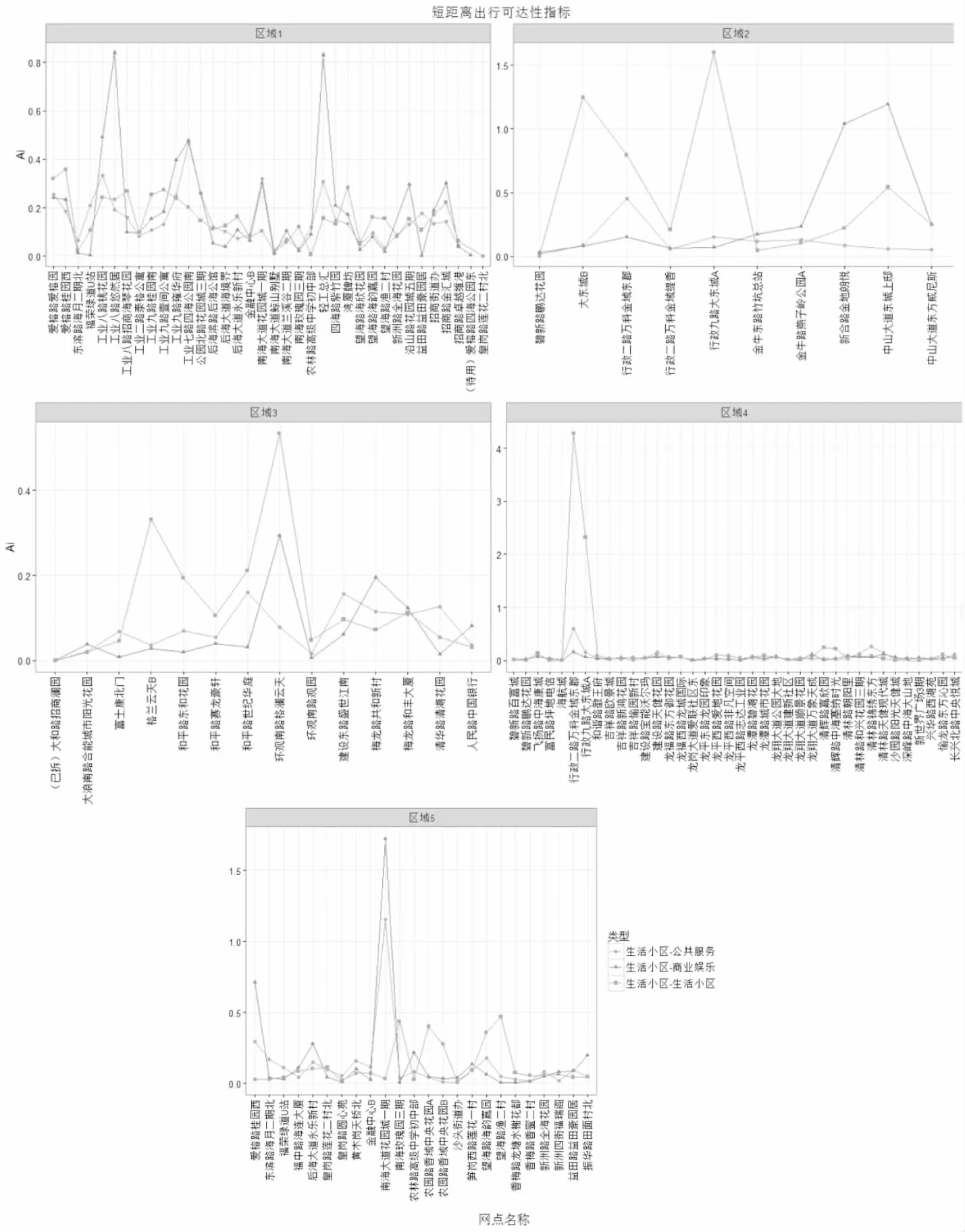
Figure 6 Reachability index of the node from the living area type network to public service,living area,commercial entertainment type network图6 生活小区-生活小区、商业娱乐、公共服务网点可达性指标

Figure 7 Potential index of the of the node from the living area type network to public service,living area and commercial entertainment type network图7 生活小区-生活小区、公共服务、商业娱乐网点潜力容量分析图

生活小区⁃公共服务/%生活小区⁃商业娱乐/%生活小区⁃生活小区/%区域131.7336.8031.47区域213.0031.5555.46区域328.6223.5347.85区域418.1211.8270.01区域530.1631.3638.48
前文在长距离出行分析得出交通枢纽-商业娱乐的相对可达性较低,容量潜力较小;而在以生活小区为核心的中短距离衔接区域中,到达各服务类型的网点相对潜力较均衡,生活小区到生活小区自身的相对潜力较大,表明在中短距离衔接中,人们出行的目的地很大可能会是生活小区。
4.4 关键节点筛选评价
本文设计了一种针对用户出行目的和出行距离为基础的分区可达性和网络容量潜力模型筛选关键节点的优化分析方法,为了论证该方法的合理性和准确性,与传统复杂网络中经典的度值和介数方法进行比较分析,结果如图8所示。

Figure 8 Screening evaluation comparison chart of key nodes图8 关键节点筛选评价对比图
从图8中可见,利用经典的度值和介数法筛选出的关键节点,用此法大部分均可筛选出来,并且采用本方法能更加充分反映出各个网络关键节点的特征,从而为关键节点的优化提供更准确的决策支持。复杂网络分区可达性指标潜力评价模型算法明显优于传统的经典分析方法,能为关键节点的重要性指标给出评价原型,从而为其节点优化提供更准确的理论依据。该参数模型能作为一般性指标引入复杂网络中进行关键节点的选取,具有较好的推广性。
5 结束语
通过公共自行车运营数据进行复杂网络分析,包括其整体的基本拓扑分析和分区模型下的可达性潜力指标分析,对现有公共自行车运营情况进行了整体分析和交通可达性分析,并提出网络关键节点选取模型。文中所提出的复杂网络分区可达性指标潜力评价模型,基于公共自行车的特殊交通特性,进行分区划分,能较清晰地展示系统中重要的关键网点,并给出关键节点的交通特性,能为其进一步优化提供理论依据。
[1] Gao Zi-you,Zhao Xiao-mei,Huang Hai-jun,et al.Research on problems related to complex networks and urban traffic systems[J].Journal of Transportation Systems Engineering and Information Technology,2006,6(3):41-47.(in Chinese)
[2] Borgnat P,Abry P,Flandrin P,et al.Shared bicycles in a city:A signal processing and data analysis perspective [J].Advances in Complex Systems,2011,14(3):415-430.
[3] Zheng Xiao, Chen Jian-ping, Shao Jia-li,et al.Analysis on topological properties of Beijing urban public transit based on complex network theory[J].Acta Physica Sinica,2012,61(19):95-105.(in Chinese)
[4] Deng Yu,Cai Jian-ming,Yang Zhen-shan,et al.Measuring time accessibility with its spatial characteristics in urban areas of Beijing[J].Acta Geographica Sinica,2012,67(2):169-178.(in Chinese)
[5] Liu Zhi-lin,Wang Mao-jun.Job accessibility and its impacts on commuting time of urban residents in Beijing:From a spatial mismatch perspective[J].Acta Geographica Sinica,2011,66(4):457-467.(in Chinese)
[6] Chen Jing. Reachability analysis on real-time value-passing systems[J].Chinese Journal of Computers,2003,26(1):19-25.(in Chinese)
[7] Hu F, Liu Y, Jin J. Multi-index evaluation algorithm based on locally linear embedding for the node importance in complex networks[C]∥Proc of the 13th International Symposium on Distributed Computing and Applications to Business,Engineering & Science(DCABES 2015), 2015:138-142.
[8] Shang Yan,Fan Xin-wei,Yu Hong.A novel node influence measurement algorithm based on characteristics of users and propagation[J].Computer Engineering & Science,2015,37(11):2105-2111.(in Chinese)
[9] Zhou Xuan,Zhang Feng-ming,Li Ke-wu,et al.Finding vital node by node importance evaluation matrix in complex networks[J].Acta Physica Sinica,2012,61(5):1-7.(in Chinese)
[10] Du Y,Gao C,Hu Y,et al.A new method of identifying influential nodes in complex networks based on TOPSIS[J].Physica A Statistical Mechanics & Its Applications,2014,399(4):57-69.
[11] Peng Ya-li, Lü Ling,Xie Zhong-fu,et al.Research on layered-partition communication model on intelligent Urban VANET[J].Journal of Jiangxi Normal University (Natural Science),2016,40(6):627-634.
[12] Wang Jiao-e, Mo Hui-hui,Jin Feng-jun.Spatial structural characteristics of Chinese aviation network based on complex network theory[J].Acta Geographica Sinica,2009,64(8):899-910.(in Chinese)
附中文参考文献:
[1] 高自友,赵小梅,黄海军,等.复杂网络理论与城市交通系统复杂性问题的相关研究[J].交通运输系统工程与信息,2006,6(3):41-47.
[3] 郑啸,陈建平,邵佳丽,等.基于复杂网络理论的北京公交网络拓扑性质分析[J].物理学报,2012,61(19):95-105.
[4] 邓羽,蔡建明,杨振山,等.北京城区交通时间可达性测度及其空间特征分析[J].地理学报,2012,67(2):169-178.
[5] 刘志林,王茂军.北京市职住空间错位对居民通勤行为的影响分析——基于就业可达性与通勤时间的讨论[J].地理学报,2011,66(4):457-467.
[6] 陈靖.时间符号迁移图上的可达性分析[J].计算机学报,2003,26(1):19-25.
[8] 尚焱,樊欣唯,于洪.考虑用户和传播属性的节点影响力评估算法[J].计算机工程与科学,2015,37(11):2105-2111.
[9] 周漩,张凤鸣,李克武,等.利用重要度评价矩阵确定复杂网络关键节点[J].物理学报,2012,61(5):1-7.
[12] 王姣娥,莫辉辉,金凤君.中国航空网络空间结构的复杂性[J].地理学报,2009,64(8):899-910.

