基于IMU的主动伴舞机器人人机协作控制算法*

刘 召，宋立滨，于 涛，郭 凯，王增喜，耿美晓

(1.清华大学天津高端装备研究院，天津 300304;2.清研华宇智能机器人(天津)有限责任公司，天津 300304)

1 引言

自传统工业机器人诞生以来，机器人技术在短短的60年内便取得了显著的进步。如今，机器人已经不再受限于工业应用，它的研究重点和发展方向更趋向于日常生活的应用，如餐饮、迎宾、娱乐、陪伴等[1]。同时，机器人技术的发展对人机协作的主动性要求也越来越高，也就是说，机器人不仅能够根据人的施力情况而被动运动，而且能根据预先学习的知识与人协调作业，即主动协调控制[2]。

本文以主动型舞蹈机器人作为人机协作机器人的研究背景，机器人的主干外观如图1所示。主动型舞蹈机器人可以按照预先学习的舞步规则带领人完成舞蹈动作，还可以根据人在舞蹈过程中对机器人上身施加的力实时调整舞蹈轨迹，避免人受到伤害，实现人与机器人之间的协调运动，具有更高的主动性和智能性。

传统的人机协作机器人控制系统中大多采用多维力传感器来感受外力的大小和方向，以此作为控制算法的输入[3]。这种控制系统对外力的感知简便、准确，但价格十分昂贵。本文采用一个安装在机器人腰部的惯性测量单元IMU(Inertial Measurement Unit)模块来取代力传感器，通过感知机器人上身相对于稳定姿态的角度变化来判断机器人的受力大小和方向，识别人的意图，再结合预先学习的舞步规则进行运动协调，以此作为对机器人拟定轨迹的修正依据，保证带领人跳舞动作的协调性。

Figure 1 Appearance of active dancing robot图1 主动伴舞机器人外观

2 基于Kalman滤波的IMU数据融合

IMU模块包含1个3轴陀螺仪和1个3轴加速度计。加速度计对载体的加速度变化敏感，取瞬时值计算倾角的误差比较大；陀螺仪数据通过积分得到的倾角不受加速度的影响，短时间内精度较高，但随时间的增加，积分累积误差和温度漂移带来的误差较大，甚至有可能导致结果发散。因此在舞蹈机器人实时姿态判断算法中，需要使用Kalman滤波算法，利用加速度计和陀螺仪各自的特点将数据进行融合，以抑制误差，提高测量精度[4,5]。

本文采用陀螺仪建立的机器人上身姿态模型如下所示：

αk=αk-1+(uk-1-βk-1)T

其中，α为机器人上半身的姿态角，u为陀螺仪角速度测量值，β为陀螺仪稳态漂移，T为采样时间。

状态估计时，认为陀螺仪稳态漂移为固定值，即：

βk=βk-1

将这两个方程写成矩阵形式，即得到：

(1)

由此可得采用卡尔曼滤波进行数据融合算法过程[6]：

(1)建立系统状态方程：

X(k)=AX(k-1)+Buk-1

(2)

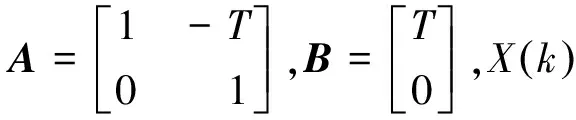
(2)由上一次的误差协方差P(k-1)和过程噪声预测新的误差P(k)：

P(k)=AP(k-1)AT+Q

(3)

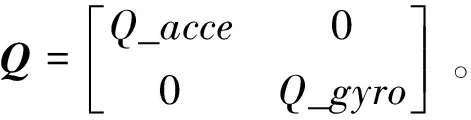
其中，Q_acce为加速度计的协方差，Q_gyro为陀螺仪测量协方差，其数值代表卡尔曼滤波器对其传感器数据的信任程度，值越小，信任度越高。

(3)计算卡尔曼增益。

Kg(k)=P(k)HT(HP(k)HT+R)-1

(4)

(4)进行校正更新，得到状态k的最优估算值X(k)：

X(k)=X(k-1)+Kg(k)(Z(k)-HX(k-1))

(5)

其中，Z(k)为k时刻的系统测量值。

(5)为下一步估计k+1状态最优值迭代进行更新操作，并更新k状态协方差P(k)值：

P(k)=(I-Kg(k)H)P(k-1)

(6)

其中，I为单位矩阵。

计算完时间更新和测量更新后，再次重复上一次计算得到的后验估计，作为下一次计算的先验估计，如此循环运算直到找到最优的结果为止，由此便得到了主动伴舞机器人判断人施力状况的姿态角。

3 舞蹈机器人人机协作控制算法

主动型伴舞机器人的运动状态由两部分合成，第一部分是机器人根据预先学习的舞步规则得到的目标坐标和期望速度矢量；另一部分是人类舞伴对机器人的实时作用力产生的人为速度矢量。系统根据两个速度矢量的和对机器人执行开环速度控制。

(7)

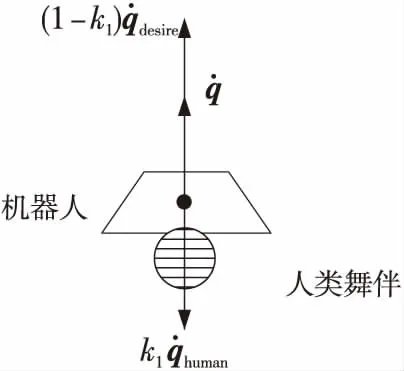
Figure 2 Composite velocity of the robot图2 机器人受合速度示意图

3.1 机器人主动运动轨迹

主动型舞蹈机器人按照预先学习的舞步规则，配合预定的伴奏音乐，确定轨迹坐标序列及时间序列。假定在某一段轨迹上，机器人原始的运动规律可表示为：

ydi=fdi(x)

θdi=gdi(x)

(8)

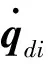
3.2 人力对机器人运动影响算法

机器人的上身和下身通过装有弹簧的圆盘连接，将IMU水平放置在腰部的圆盘上，当人对机器人上身产生推拉或扭转的作用力时，IMU的实时输出值就会发生变化，经Kalman滤波后就会反应到横滚角、俯仰角和扭转角的变化上，由此来判断人对机器人作用力的大小和方向。机器人则在带领人跳舞的同时，根据人力的大小判断人的意图，向人力做出妥协，避免人受到伤害。

3.2.1 相对姿态角求解

由于机械结构误差和安装误差，机器人上身姿态角的静态值不可能永远为零，因此就需要人为对姿态角进行校正。

当机器人静止，不受到外力作用时，连续测量、求取N次机器人三个方向姿态角，取平均值，得到静止状态下机器人的横滚角Rool0、俯仰角Pitch0和扭转角Twist0。机器人运动时，实时计算三个方向姿态角，并与静止姿态角做差，得到理想状态下的相对姿态角：

Rollre=Roll-Roll0

Pitchre=Pitch-Pitch0

Twistre=Twist-Twist0

(9)

但是,在实际的机器人模型上，连接弹簧的刚度值要同时兼顾对外力的响应变化和保持运动过程的相对稳定，因此机器人运动过程中上身的小幅度摆动不可避免。综合考虑以上情况，要根据机器人独立运动时三个姿态角的抖动，选择合适的阈值调整相对姿态角的大小。调整后的相对姿态角表达式如式(10)所示：

(10)

其中，p、q、m分别为姿态角的抖动误差。

3.2.2 相对姿态角到运动速度矢量的映射

在人力作用下，机器人上身姿态角随作用力的增大而单调递增，但力过大时会造成弹簧的刚性形变，机器人结构会被损坏；同时，为避免机器人运动过程中的剧烈晃动，选择的弹簧刚度较大，一般的人力无法使弹簧发生十分大的形变，所以作用力必须小于一个最大值，姿态角也相应地收敛。在数学函数表达式中，指数函数可以很好地表达这一特性，因此，人作用力大小与姿态角的关系可以用指数函数表示，具体由式(11)来表示：

Fhuman=Fmax(1-e-b θ),|θ|≤θmax

(11)

其中,θ为机器人上身受外力作用下的姿态角(横滚角/俯仰角/扭转角)，θmax为弹簧系统允许的最大姿态角度的大小，b决定指数函数曲线斜率变化规律，通过实验获得最佳取值。

由此可得机器人在人类舞伴作用力下的动力学方程：

(12)

3.2.3 基于状态判断的运动决策

在得到相对姿态角与机器人动力学关系后，并不能直接用于人机协作的运动计算，需要结合机器人当前状态来判断此刻的数据是否有效，因为例如在机器人静止状态下，我们并不希望一个突然的、瞬时的力影响机器人的状态。

3.3 人力对机器人运动影响算法

机器人在运动过程中，我们以50 Hz的频率向机器人发送速度控制信号。根据式(7)的合速度矢量表达式，可得Δt时间段内机器人的运动轨迹长度：

(13)

则机器人运动到第i个目标点时的位姿表达式为：

(14)

由于人类舞伴的作用力使原始轨迹坐标有所改变，因此第i个目标点后的轨迹点坐标都要同时做出修正。

4 实验与测试

针对本文提出的人机协作控制算法，进行了华尔兹中CCL(Closed Change Left)舞步的人机协作实验，机器人自主运动且无人力作用时，CCL舞步的期望轨迹如图3所示。

Figure 3 Diagram of desired CCL trajectory图3 CCL舞步期望轨迹示意图

两次实验中，在机器人走CCL舞步中途，人类舞伴对机器人分别施加一段时间的“推动力”和“拉力”，IMU采集到的加速度、角速度数据经卡尔曼滤波后，得到的横滚角、俯仰角和扭转角曲线分别如图4所示。

Figure 4 Curves of attitude angle when pushing the robot图4 人推动机器人时姿态角变化曲线

由图4中可以看出，推动、拉动机器人时的敏感变量为俯仰角，其随人力呈现较为明显的变化，但其余两个姿态角也有不同幅度的变化，但变化相对较小。经阈值滤波后，相对姿态角曲线如图5所示。

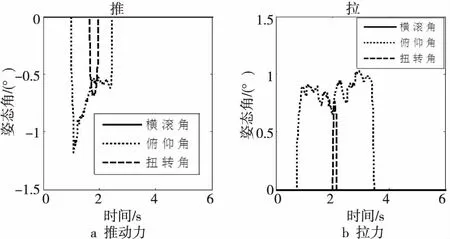
Figure 5 Curves of relative attitude angle图5 相对姿态角变化曲线

在CCL舞步中，在人推动或者拉动机器人时，希望机器人向前幅度变小或变大，但并不希望其旋转，因此通过状态判断，就可以剔除扭转角的瞬时变化。在人机协作状态下，机器人实际运动轨迹与期望轨迹的对比曲线分别如图6所示。

Figure 6 Curve comparison of the desired trajectory and man-machine collaboration trajectory图6 期望轨迹与人机协作轨迹对比曲线

实验结果表明，本文算法在机器人实际运动中有效且效果较好。

5 结束语

本文针对主动型伴舞机器人的人机协作问题进行了研究，提出了基于IMU的人机协作控制方式。通过卡尔曼滤波算法将加速度计和陀螺仪产生的实时加速度和角速度进行融合，得出舞蹈机器人上身的实时姿态角，通过姿态角的变化判断人类舞伴对机器人的作用力，从而机器人可以根据人力的作用实时修改轨迹，完成人和机器人的协调动作，避免人受到伤害。实验结果验证了算法的有效性。

[1] Tan Min, Wang Shuo. Research progress on robotics [J].ACTA Automatica Sinica,2013,39(7):963-972.(in Chinese)

[2] Wang Ting,Wang Yue-chao.Human-machine system and its application to mobile robot [J].Robot,2004,26(6):553-557.(in Chinese)

[3] Kosuge K,Hayashi T,Hirata Y,et al.Dance partner robot:MS Dancer [C]∥Proc of the 2003 IEEE/ RSJ International Conference on Intelligent Robots and Systems,2003:3459-3464.

[4] Feng Zhi-yong, Zeng Han,Zhang Li,et al.Angle measurement based on gyroscope and accelerometer signal fusion [J].Journal of Southwest China Normal University (Natural Science Edition),2011,36(4):137-141.(in Chinese)

[5] Wang Shuai,Wei Guo.Application of Kalman filter in attitude measurement for four-rotor aircraft flight[J].Ordnance Industry Automation,2011,30(1):73-74.(in Chinese)

[6] Peng Ding-cong.Basic principle and application of Kalman filter [J].Software Guide,2009,8(11):32-34.(in Chinese)

附中文参考文献：

[1] 谭民，王硕.机器人技术研究进展[J].自动化学报,2013,39(7):963-972.

[2] 王挺，王越超.人机系统在移动机器人平台的应用[J].机器人,2004,26(6):553-557.

[4] 冯志勇，曾瀚，张力，等.基于陀螺仪及加速度计信号融合的姿态角度测量[J].西南师范大学学报(自然科学版),2011,36(4):137-141.

[5] 王帅，魏国.卡尔曼滤波在四翼飞行器姿态测量中的应用[J].兵工自动化,2011,30(1):73-74.

[6] 彭丁聪.卡尔曼滤波的基本原理及应用[J].软件导刊,2009,8(11):32-34.