基于数据挖掘技术的气温敏感负荷短期预测研究
刘蓉晖,赵才涛
(上海电力学院电气工程学院,上海 200090)
随着我国智能电网技术和装备的快速发展,供电系统的建设也越来越复杂,使得一些负荷更易受气象因素[1]等外界环境的干扰。同时,监测点负荷数据的急剧增加,导致从中找出有利于负荷预测的信息困难加大,这些都不利于负荷的准确预测。因为负荷预测在电力系统的规划、设计、负荷调度、控制、能源管理等方面起着重要作用,所以提高负荷预测精度对电网的安全、稳定、优化与经济运行有着重要的意义[2]。因此需要不断完善各方面的信息以及优化预测模型来提高负荷预测精度。
提高负荷预测精度不仅要考虑影响负荷变化的因素,还需要合理的预测方法。国内外学者对负荷预测提出了多种方法,常见的预测方法有时序分析法、回归分析法、神经网络法、支持向量机法以及综合分析法等[3-5]。文献[6]中将大数据分析技术运用于智能电网的建设中,基于数据挖掘技术进行短期电力负荷预测,有效地提高了负荷预测的速度和精度。文献[7]中运用大数据管理技术结合随机森林算法,基于Hadoop预测平台进行负荷预测,在不同的数据集上运用此方法进行负荷预测可有效提高预测的精度。文献[8]中引入元胞概念,通过对元胞进行聚类,分成多个等级,然后针对不同的等级运用支持向量机模型进行负荷预测,这样可以提高预测的有效性与适应度。文献[9]中考虑了影响负荷变化的气象因素,并运用修正模型对预测结果进行修正,可使预测结果更加精确。
基于以上分析,本文提出一种考虑气象因素的基于改进K-means聚类的ARMA预测模型对短期气温敏感负荷进行预测。首先通过改进的K-means聚类算法对负荷和气温进行聚类分析,建立负荷与气温的关系函数;其次,经过聚类分析后在各个簇内建立相应的ARMA预测模型,考虑气温和湿度因素;最后,对各个簇内的预测结果进行修正、综合,通过平均相对误差来评判预测的好坏。文中通过单纯的ARMA预测法,考虑气象因素的基于K-means聚类的ARMA预测法以及本文的改进法进行实例分析对比,实验结果证明了本文所提出的方法可有效提高负荷预测的精度和效率。
1 数据挖掘技术
1.1 数据预处理
数据在监测平台采集后,经过传输、存储等一系列过程处理后组成数据库,但在这一系列过程中都有可能使数据损坏[10]。因此在运用采集的数据之前必须对数据进行预处理。本文中所用到的预处理技术包括数据清理、数据转换和增补缺失值等。
1.2 K-means聚类
聚类就是将大量的数据分成不同的簇,每一个簇内的数据彼此间有某种联系或有相似之处,簇与簇之间有一定的界限或区别,通过整体结构的不同或层次的区别来寻找这些数据之间隐藏的关系。因为K-means聚类算法具有计算时间短、速度快、容易解释、聚类效果较好等优点[11-13]而被广泛运用。
1.2.1 传统的K-means聚类算法
传统K-means聚类算法的基本步骤如下:
1)在一个数据集N={N1,N2,…,Nn}中,选取K个点作为聚类的初始中心Sj(j=1,2,…,K)。
2)计算数据集中各个点到中心点的距离,即Dj=|Ni-Sj|,按照就近原则,根据各数据点离自身周围哪个聚类中心近的就划分在哪个簇内,从而形成K个簇Ck(k=1,2,…,k)。
3)计算各簇内样本Nj到聚类中心Si的距离平方和E,如式(1)所示。
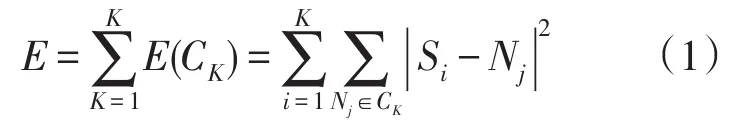
4)对每个簇内对象作均值处理,将计算后的结果作为新的聚内中心。
5)检查E和聚类中心是否发生变化,若发生变化则跳转步骤2)重新计算,直到不变化为止。
1.2.2 改进的K-means聚类算法
由于传统聚类方法的聚类个数是由用户自己选定的,根据具体情况分析易受人为主观和经验的影响,这样的聚类数具有不确定性,而且初始聚类中心也是随机选取的,具有盲目性,这会使聚类更耗时,且结果不准确。本文为了得到较好的聚类结果,提出引入Davies—Bouldin指数[14],通过DB指数的值来选取聚类数K。DB指数可由式(2)-(5)求得:
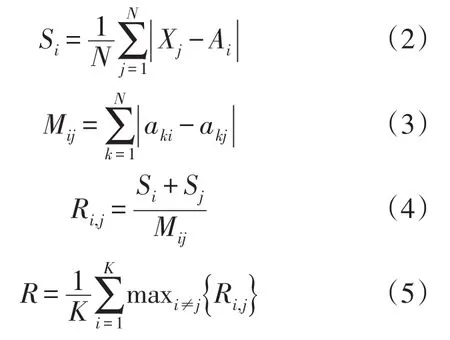
式(2)中Si为第i个簇的分散度值,Xj为第i个簇的第j个数据值,Ai为第i个簇的中心点,N为第i个簇的数据点个数。式(3)中Mij为第i个簇与第j个簇的距离,aki,akj分别为各个簇的中心点的第K个属性值。式(4)中Ri,j是第i个簇与第j个簇的相似度。将式(2)、(3)、(4)代入式(5)可求得DB指数值R,其中K为聚类个数。当K变化时R也随之变化,R越小表明簇内数据越紧密且簇与簇之间的分离性越好,聚类效果越好。因此R最小时可选取最优聚类数K。
对于初始聚类中心,本文采用文献[15]所提的通过簇内对象密度的大小来选取,簇内对象密度越大,说明簇内对象越集中,聚类效果越好。设对象集合X={x1,x2,…,xn},xi=(xi1,…,xim),不同对象xi和xj的欧式距离d(xi,xj)可由式(6)求得。

对象集X的平均密度Ave_Den(X)如式(7)所示。
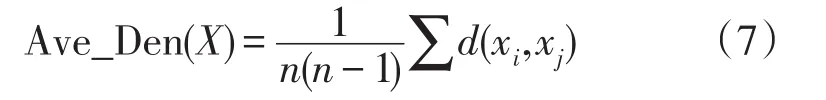
对任一对象xi的密度Den(xi)如式(8)所示。
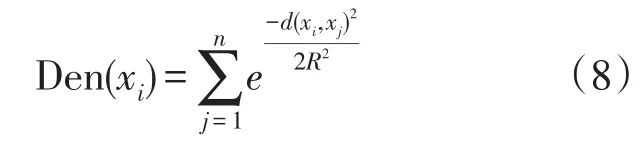
其中R为以对象xi为圆心的圆的半径,且xi到其他点的距离满足0<d(x,xi)<R。将所有密度构成一个集合,选取其中密度最大的对象作为第一个初始聚类中心,按大到小以此类推,将第K个最大密度对象作为第K个簇的初始聚类中心,且每个簇的密度要大于平均密度,按照就近原则将各个对象分配到附近的簇内。
2 模型的建立
2.1 气温模型的建立
本文所考虑的气象因素主要是气温和相对湿度,两者间有一定的相关关系。在夏季当气温高于某一温度TH时,实际温度可以由式(9)表示。在冬季当气温低于某一温度TL时,实际温度可以由式(10)表示。其他情况下当气温在TL到TH之间时,湿度对气温的影响很小,可以忽略不计[16]。

TA、TB为有效气温,a、b为常系数,需根据实际预测需要取值,T为实际气温,H为相对湿度。
2.2 ARMA预测模型的建立
自回归移动平均模型(ARMA)由自回归模型(AR)和移动平均模型(MA)组成,是较为成熟的时间序列模型,广泛应用于电力负荷预测中。ARMA模型如式(11)所示[17],式中的预测负荷由两部分主成:第一部分为t时刻之前的负荷序列值,第二部分为t时刻及t时刻之前的负荷误差值。Lt为t时刻的电力负荷,p、q分别为AR和MA的阶数,α是自回归系数,β是滑动平均系数,et为t时刻的误差,符合正态分布。

当运用ARMA模型进行负荷预测时考虑气象因素会使预测结果更加精确,但是,ARMA模型是一个线性模型,它不能完全描述气象因素与非线性负荷的关系,一旦气象因素发生较大的变化,就会引起过度拟合,使预测精度大大降低。因此,需要对预测结果进行相应的修正,修正模型如式(12)所示,式中ΔL是负荷修正值,ΔT是温度的变化值,L1-L0是负荷变化值,ΔT′是预测日与预测日前一天的温度差。

3 实例分析
本文研究的是上海市某配电网负荷,为典型的办公、居民负荷,具有很强的周期性和季节性。一般工作日负荷比周末负荷更重要,所以本文只对工作日负荷作重点研究。城市负荷中易受气象因素影响的气温敏感性负荷越来越多,一般夏季和冬季较为明显,这会加大负荷预测的误差。为提高负荷预测精度,本文在预测时不仅考虑了气象因素,而且还运用数据挖掘技术进行预测前的预处理工作。
3.1 基于改进K-means聚类的负荷分析
文中所选数据为2011年5月1日至2012年5月1日电网监测点的负荷数据,以每小时的采样点为采样数据,共选取8 760个采样数据,并选取与负荷数据时刻相对应的气温、相对湿度数据,建立对象数据集进行数据分析。
3.1.1 聚类数K的选取
对所选目标对象分别用传统K-means聚类算法和改进的K-means聚类算法进行6次比对聚类分析,并引用文献[18]中聚类质量评估方法对聚类结果进行评价,选取最优K值作为聚类数。表1为两种聚类算法的结果比较,从表中可以看出随着K值得增大聚类的准确率及所耗时间均会增加,对于改进的K-means算法,K值是确定的,取K=4且聚类准确率和时耗都比较理想,通过两种聚类算法的结果对比可以说明提出的改进K-means聚类算法不仅可以确定聚类数K,而且聚类效果也较好。
3.1.2 负荷与气温关系的聚类分析
图1为2011-2012年负荷与气温的聚类图。从图中可知负荷与气温的关系可以表示成三部分:第一部分是当温度T<Tl时,此时Tl=15℃,负荷与温度呈负相关性,系数比为-Kl,表示当温度低于一定范围时,负荷会随着温度的降低而增大,说明气温越低取暖负荷越大;第二部分是当温度Tl≤T≤Th时,此时Th=25℃,负荷基本不受温度的影响,说明此范围内的负荷基本属于日常的基础负荷LB;第三部分是当温度T>Th时,负荷与温度呈正相关性,系数比为Kh,表示当温度高于一定范围时,负荷会随着温度的升高而增大,说明气温越高降温负荷越大。在一般情况下,对于城市负荷而言,降温负荷所需的用电量往往要大于取暖负荷所需的用电量,即系数K1<Kh。综上所述,负荷与气温的函数关系可由式(11)表示,与其对应的曲线图如图2所示。

表1 K-means聚类算法与改进K-means聚类算法比较Tab.1 Comparison of K-means clustering algorithm and improved K-means clustering algorithm
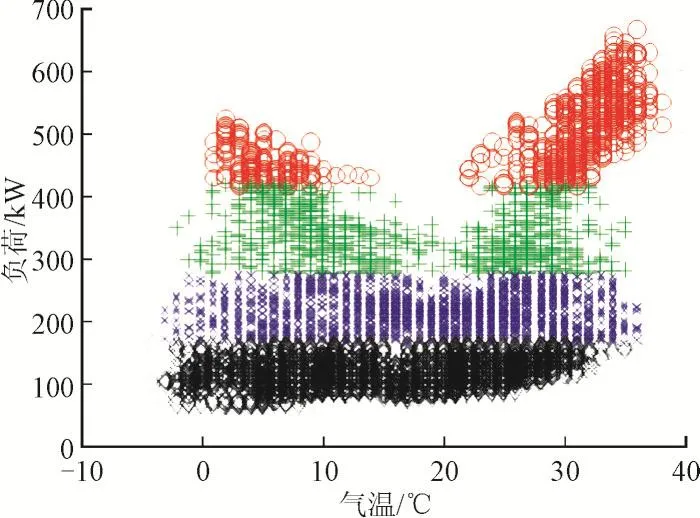
图1 2011-2012年负荷—气温的聚类图Fig.1 The clustering figure of load and temperature from 2011 to 2012
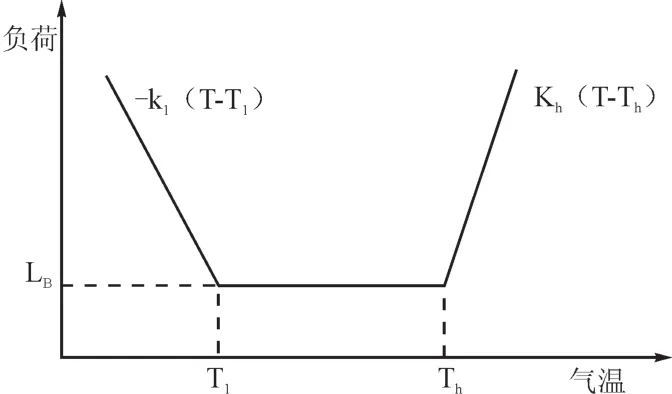
图2 负荷与气温的关系曲线图Fig.2 The relation curve of load and temperature

3.2 基于改进K-means聚类的负荷预测
本文基于数据挖掘技术,运用时间序列分析技术对气温敏感性负荷进行预测分析,结合二者的优点可以实现快速而精准的预测。基于数据挖掘技术的ARMA预测方法流程如图3所示,主要分为以下几部分:

图3 负荷预测流程图Fig.3 Flowchart of the load forecasting
1)提取监测点的目标数据集进行预处理,并查找与之对应的气象数据建立对象数据集。
2)基于改进K-means聚类算法对负荷和气温进行聚类分析,按照负荷与气温的关系分成不同的簇,考虑气象因素,在各个簇内进行相应的负荷预测。
3)对各预测结果进行相应的修正、综合、误差评估,从而得出结论。
3.2.1 数据的选取
经分析可知,春、秋季节气温、湿度对负荷变化影响较小,与之相比,夏、冬季节的影响较大。所以本文主要选取配电网2011年5月1日至2012年5月1日夏季和冬季的监测数据作为历史负荷数据,并选取2012年7月和2013年1月各一个工作日的最大日负荷数据作为预测样本进行季节性的负荷预测,再选取2012年7月6日一天24h的负荷进行预测,通过比较分析3种预测方法的预测结果来证明本文所提方法的有效性。
3.2.2 预测结果分析
通过模型预测的结果需要经过评价指标来说明预测的精确度,一般选取平均相对误差来进行评估。式(12)为平均相对误差表达式。

表2为2012年7月和2013年1月夏季和冬季各一个工作日的负荷预测结果。从表2可知,夏季一个工作日的总平均相对误差为1.78%,冬季一个工作日的总平均相对误差为1.48%,相比于文献[7]、[8]、[10]所用的预测方法,本文所提的方法能更有效地提高预测的精度。从表中还可得知夏季的气象因素对负荷的影响要大于冬季,致使夏季负荷预测的误差要比冬季大。

表2 工作日负荷预测结果Tab.2 Load forecasting results of workday
图4为对应表2中7月16日至20日三种预测方法的工作日负荷预测误差,其中e1为不考虑气象因素的单纯ARMA负荷预测误差,e2为考虑气象因素的基于传统K-means聚类的ARMA负荷预测误差,e3为本文所提考虑气象因素的基于改进K-means聚类的ARMA负荷预测误差。从图4可以得知本文所提方法相比于其他两种方法能有效降低负荷预测的误差,提高预测精度。
表3为2012年7月6日的日负荷预测结果,其对应的曲线图如图5所示。单纯ARMA负荷预测值用L1表示,预测误差用e1表示;考虑气象因素的基于传统K-means聚类ARMA负荷预测值用L2表示,预测误差用e2表示;本文所提方法的预测值用L3表示,预测误差用e3表示。从表3可知,L1的日平均相对误差为3.95%,L2的日平均相对误差为2.31%,L3的日平均相对误差为1.9%。通过比较发现本文方法可以提高负荷预测精度。
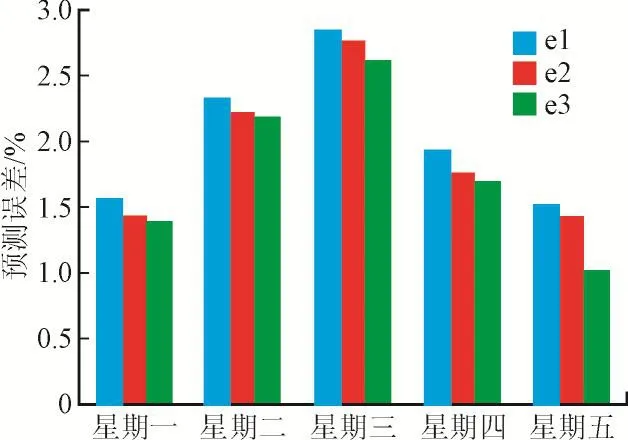
图4 三种预测方法的工作日负荷预测误差Fig.4 Load forecasting errors of working days with three kinds of prediction methods

表3 2012年7月6日的负荷预测结果Tab.3 Load forecasting results on July 6,2012
4 结论
针对气温敏感性负荷,本文提出一种由数据挖掘技术和ARMA预测模型相结合的负荷预测方法,在考虑了气温、湿度等因素的影响后,通过建立气温与湿度的关系函数,运用数据挖掘技术对历史数据进行预处理,并对负荷与气温进行聚类分析,然后在不同簇内进行相应的负荷预测,最后对预测结果进行修正与综合。通过比较本文方法与传统方法所得到的预测结果,可以得到本文所提方法能够有效提高负荷预测的精度和效率,为电力部门在运行管理与调度负荷时提供更好的技术支撑。
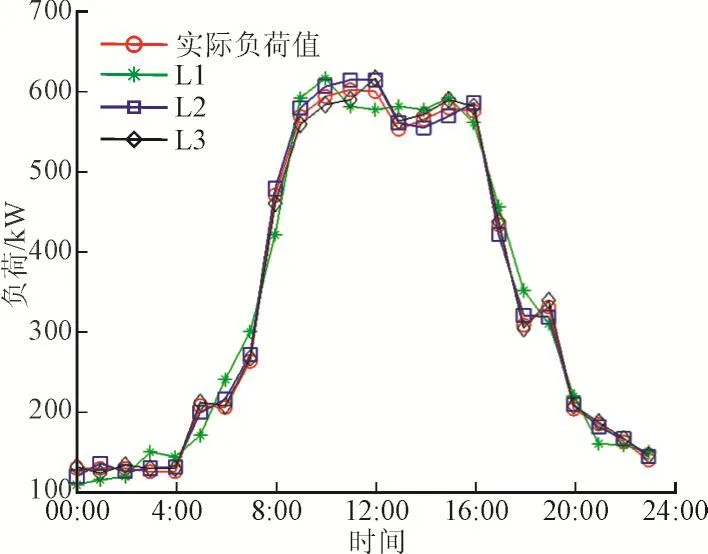
图5 2012年7月6日的负荷预测结果Fig.5 Forecasting results on July 6,2012
文中通过单纯的ARMA预测方法、考虑气象因素的基于传统K-means聚类的ARMA预测方法和本文所提的考虑气象因素的基于改进K-means聚类的ARMA预测方法进行比较分析可知:
1)改进的K-means聚类算法可解决传统K-means算法聚类数不确定,初始聚类中心随机选取的缺点,可有效提高聚类算法的准确率和效率。
2)预测中考虑了气象因素,建立气温与湿度的关系函数,并且在聚类的基础上进行负荷预测,而且对预测结果进行相应修正,这样能有效提高负荷预测的精度。
3)通过三种预测方法的比较分析可知,在进行负荷预测时考虑影响因素越多,技术越成熟,预测结果会越精确,从预测结果可以验证本文所提方法的有效性。
[1] 王惠中,刘珂,周佳.基于综合气象指数和日期类型的电力系统负荷预测[J].电网与清洁能源,2015,31(9):67-71.WANG Huizhong,LIU Ke,ZHOU Jia.Power system load forecasting based on comprehensive meteorological index and date type[J].Power System and Clean Energy,2015,31(9):67-71.
[2] 全思平,吴浩.基于数据挖掘技术的短期电力负荷预测[J].电力信息与通信技术,2014,12(3):95-98.QUAN Siping,WU Hao.A short-term power load forecast⁃ing system using the data mining technology[J].Electric Pow⁃er ICT,2014,12(3):95-98.
[3] 廖旎焕,胡智宏,马莹莹,等.电力系统短期负荷预测方法综述[J].电力系统保护与控制,2011,39(1):147-152.LIAO Nihuan,HU Zhihong,MA Yingying,et al.Review of the short-term load forecasting methods of electric power system[J].Power System Protection and Control,2011,39(1):147-152.
[4] 王玉龙,崔玉,李鹏,等.基于小波分析改进的神经网络模型电力系统负荷预测[J].电网与清洁能源,2015,31(2):16-20,27.WANG Yulong,CUI Yu,LI Peng,et al.Load forecasting of power system based on wavelet analysis improved neural network model[J].Power System and Clean Energy,2015,31(2):16-20,27.
[5]KYUNG BIN Song,SEONG KWAN Ha,JUNG WOOK Park,etal.Hybrid load forecasting method with analysis oftemperature sensitivities[J].IEEE Transactionson Power Systems,2006,21(2):869-876.
[6]ZHANG Pei,WU Xiaoyu,WANG Xiaojun,et al.Shortterm load forecasting based on big data technologies[J].CSEE Journal of Power and Energy Systems,2015,1(3):59-67.
[7] 王德文,孙志伟.电力用户侧大数据分析与并行负荷预测[J].中国电机工程学报,2015,35(3):527-537.WANG Dewen,SUN Zhiwei.Big data analysis and parallel load forecasting of electric power user side[J].Proceedings of the CSEE,2015,35(3):527-537.
[8] 肖白,聂鹏,穆钢,等.基于多级聚类分析和支持向量机的空间负荷预测方法[J].电力系统自动化,2015,39(12):56-61.XIAO Bai, NIE Peng, MU Gang, et al.A spatial forecasting method based on multilevel clustering analysis and support vector machine[J].Automation of Electric Power Systems,2015,39(12):56-61.
[9] 方鸽飞,胡长洪,郑奕辉,等.考虑夏季气象因素的短期负荷预测方法研究[J].电力系统保护与控制,2010,38(22):100-104.FANG Gefei, HU Changhong, ZHENG Yihui, et al.Study on the method of short-term load forecasting considering summer weather factors[J].Power System Protection and Control,2010,38(22):100-104.
[10]陈红坤,黄娟.数据挖掘及其在电能质量分析中的应用[J].电力系统及其自动化学报,2009,21(5):51-55.CHEN Hongkun,HUANG Juan.Data mining and its application in power quality analysis[J].Proceedings of the CSU-EPSA,2009,21(5):51-55.
[11]RAJESWARI K,OMKAR ACHARYA,MAYUR SHAR⁃MA,et al.Improvement in k-means clustering algorithm using data clustering[J].Computing Communication Con⁃trol and Automation,2015(9):367-369.
[12]李春生,王耀南.聚类中心初始化的新方法[J].控制理论与应用,2010,27(10):1435-1440.LI Chunsheng,WANG Yaonan.New initialization method for cluster center[J].Control Theory&Applications,2010,27(10):1435-1440.
[13]熊忠阳,陈若田,张玉芳.一种有效的K-means聚类中心初始化方法[J].计算机应用研究,2011,28(11):4188-4190.XIONG Zhongyang,CHEN Ruotian,ZHANG Yufang.Effective method for cluster centers'initialization in K-means clustering[J].Application Research of Computers,2011,28(11):4188-4190.
[14]DAVID L.DAVIES and DONALD W.BOULDIN.A clustering separation measure.IEEE Transactions on Pattern Analysis and Machine Intelligence,1979.
[15]赵莉,候兴哲,胡君,等.基于改进k-means算法的海量智能用电数据分析[J].电网技术,2014,38(10):2715-2720.ZHAO LI,HOU Xingzhe,HU Jun,et al.Improved kmeans algorithm based analysis on massive data of intelligent power utilization[J].Power System Technology,2014,38(10):2715-2720.
[16]LI KE,TAI Nengling,ZHANG Shenxi.Research and ap⁃plicationofclimaticsensitiveshort-termloadforecasting[C].Power&Energy Society General Meeting,2015.
[17]HUANG Shyhjier,SHIH Kuangrong.Short-term load forecasting via ARMA model identification including nongaussion process considerations[J].IEEE Transactions on Power Systems,2003,18(2):673-679.
[18]索红光,王玉伟.一种用于文本聚类的改进k-means算法[J].山东大学学报,2008,43(1):60-64.SUO Hongguang,WANG Yuwei.An improved k-means algorithm for document clustering[J].Journal of Shandong University,2008,43(1):60-64(in Chinese).
[19]雷正新,韩蓓,聂萌,等.配电网大数据环境下的多点负荷预测算法与应用研究[J].电力系统保护与控制,2016,44(23):68-78.LEI Zhengxin,HAN Bei,NIE Meng,et al.Research and application of multi-node load forecasting algorithm under the environment of distribution network’s big data[J].Power System Protection and Control,2016,44(23):68-78
[20]孔平,陈亮,马晶.基于模糊信息粒化支持向量机的短期电力负荷预测[J].电力信息与通信技术,2016,14(1):11-14.KONG Ping,CHEN Liang,MA Jing.Short-term power load forecasting based on the fuzzy information granulation and SVM[J].Electric Power Information and Communica⁃tion Technology,2016,14(1):11-14.
[21]王新,孟玲玲.基于EEMD-LSSVM的超短期负荷预测[J].电力系统保护与控制,2015,43(1):61-66.WANG Xin,MENG Lingling.Ultra-short-term load forecasting based onEEMD-LSSVM[J].PowerSystem Protectionand Control,2015,43(1):61-66.
[22]陆玉军,李澄,陈颢,等.紧急切负荷网荷互动终端设计与实现[J].电力工程技术,2017,36(3):82-87,99.LU Yujun,LI Cheng,CHEN Hao,et al.Design and Implementation of User Terminal Unit for Emergency Load Shedding[J].Electric Power Engineering Teachnology,2017,36(3):82-87,99.
[23]林幕群,彭显刚,林利祥,等.基于数据挖掘技术的电价执行在线稽查模型[J].广东电力,2016,29(1):108-112.LIN Muqun,PENG Xiangang,LIN Lixiang,et al.Online inspection model for electricity price implementation based on data mining technology[J].Guangdong Electric Power,2016,29(1):108-112.
[24]梅沁,黄敏,徐甍.电力班组信息化负荷大数据分析系统研究及应用[J].电力信息与通信技术,2016,14(1):15-18.MEI Qin,HUANG Min,XU Meng.Study and application of power team information burden analysis system based on big data[J].Electric Power Information and Communication Technology,2016,14(1):15-18.
[25]张魁,王亚明,刘明,等.基于大数据及智能算法的连云港电量负荷预测研究[J].江苏电机工程,2016,35(3):49-52.ZHANG Kui,WANG Yaming,LIU Ming,et al.Research on electricity consumption and load prediction of lianyungang based on big data and intelligent algorithm[J].Jiangsu Electrical Engineering,2016,35(3):49-52.
[26]刘世成,刘沅昆,武昕,等.基于大数据的非侵入式负荷分解技术研究[J].电力信息与通信技术,2016,14(12):9-14.LIU Shicheng,LIU Yuankun,WU Xin,et al.Research on non-intrusive load decomposition technology based on big data[J].Electric Power Information and Communication Technology,2016,14(12):9-14.
[27]徐强,梁伟.采样数据对综合负荷模型参数辨识的影响[J].江苏电机工程,2016,35(5):53-56.XU Qiang,LIANG Wei.Effects of Sampling Data on Parameter Identification of Composite Load Model[J].Jiangsu Electrical Engineering,2016,35(5):53-56.
[28]吴飞财.无信号覆盖区域电能数据采集方法研究与应用[J].广东电力,2016,29(9):104-108.WU Feicai.Research on electric energy data acquisition method in no signal coverage areas and its application[J].Guangdong Electric Power,2016,29(9):104-108.
[29]姚珺玉,谢国财.面向运维的电网运行数据分析系统开发[J].广东电力,2016,29(10):92-96.YAO Junyu,XIE Guocai.Development of operational data analysis system for operation and maintenance of power grid[J].Guangdong Electric Power,2016,29(10):92-96.
[30]马哲,舒勤.基于ESPRIT分解算法的短期电力负荷预测[J].电力系统保护与控制,2015,43(7):90-96.MA Zhe,SHU Qin.Short term load forecasting based on ESPRIT integrated algorithm[J].Power System Protection and Control,2015,43(7):90-96.

