多重网格准线性近似技术在三维航空电磁正演模拟中的应用
殷长春,卢永超,刘云鹤,张 博,齐彦福,蔡 晶
吉林大学地球探测科学与技术学院,长春 130026
0 引言
随着我国经济的快速增长,矿产资源的消耗逐渐增多,地质条件有利地区的矿产资源已近枯竭,目标转向广大无人区。由于这些地区施工困难,常规的地面电磁法很难满足勘探需求,航空电磁法勘探因此成为重要的勘查技术手段[1]。三维积分方程正演是航空电磁数值模拟的重要技术,它通过对异常区域进行剖分,建立异常区域内电场满足的第二类Fredholm积分方程,通过直接求解或利用迭代技术求解离散后的矩阵方程得到空间电磁场。在小规模异常体模拟中,系数矩阵占用存储小,求解速度快。然而,对于大型异常体,由于形成的线性方程组系数矩阵的密实性,计算耗时多、存储量大,限制了积分方程算法的应用。
为了避免大型线性方程组的求解,提高计算效率,学者提出许多近似方法。典型的方法包括扩展Born近似[2]、准线性近似(quasi-linear or QL)[3]、准线性级数(QLSE)[4]、准解析(QA)近似和准解析级数(QASE)[5]等。然而,上述近似方法只有在满足其特定的使用条件下才能获得理想的计算结果。通过对QL技术的改进,Zhdanov等[6]实现了局部准线性近似(LQL)的频率域电磁正反演,并在对加拿大拉布拉多沃伊西湾镍-铜-钴矿航空电磁数据反演中取得了良好的效果。然而,该算法需要通过求解最小值问题来获得电反射系数,计算效率低。刘永亮等[7]提出了快速准线性近似方法,并将其应用于三维频谱激电反演研究,取得了很好的效果。针对多源问题的海洋可控源电磁正演模拟,Ueda等[8]结合积分方程(IE)和QL技术,提出了基于多重网格的准线性(MGQL)近似算法。MGQL算法的关键是假设背景场与异常场之间存在线性关系。基于MGQL技术,人们首先在粗网格上求解积分方程得到总场和异常场,进而求解粗网格上的电反射系数,并利用该系数在细网格上做线性插值得到离散后的电反射系数。在细网格上,利用电反射系数与背景场求解异常场,最后在细网格上获得接收点处的场值。与全积分方程法相比,对于大型异常体和网格剖分较多的情况,MGQL通过粗化网格可以大量节省计算时间。本文将该技术引入到多源航空电磁三维正演模拟中,由于反射系数计算在粗网格上进行,而细网格上的场值通过插值获得,因此可极大提高多源航空电磁的计算效率。
本文在MGQL算法的基础上,利用计算电磁学中的处理技术[9]优化粗网格上积分方程的计算过程,将发射源首次发射时的格林函数存储为Toeplitz矩阵形式,避免了不同源格林函数的重复计算,进而利用快速傅里叶变换(FFT)技术实现矩阵与向量的乘积[10],提升MGQL的计算效率。MGQL算法网格粗化与计算精度有关,因此在精度允许的范围内,调节粗网格大小可有效降低存储量、加快计算速度。最后,通过将本文算法结果和已发表的典型模型计算结果对比验证精度,并通过与开源代码MarcoAir对比验证本文MGQL算法的有效性。
1 MGQL正演理论
根据积分方程理论,在水平层状各向同性介质中,对麦克斯韦方程组进行变换,可得电场E与磁场H的如下求解方程[11-12]:
[Δσ(r)E(r)]dV+Eb(r'),
(1)
[Δσ(r)E(r)]dV+Hb(r')。
(2)
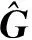
E(r)=Eb(r)+Ea(r)。
(3)
根据Zhdanov等[3]提出的准线性近似理论,假设背景场和异常场之间存在线性关系,即
(4)
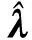
(5)

(6)
式中,EB(rj)表示异常场的Born近似[13],其表达式为
(7)
利用最小化求解方法,由式(6)可得电反射系数的求解表达式为
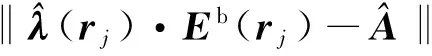
(8)
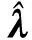
Ea(rc)=E(rc)-Eb(rc)。
(9)
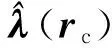
(10)
因此,式(4)可以写成独立的标量式,即
;l=x,y,z。
(11)
必须指出的是,依据公式(4)中的假设,反射系数计算虽然简单,但是如果背景场的某一个分量为零,将导致反射系数无法获取。为此,本文根据Gao等[15]提出的针对各向异性介质三维电磁感应测井的模拟算法,假设异常场和层状半空间背景场绝对值存在如下线性关系:
Ea(r)≈λ(r)·|Eb(r)|。
(12)
式中,向量λ(r)=(λx,λy,λz)。式(12)表明,在粗网格上,由于|Eb(rc)|≠0,则可以得到电反射系数的计算公式为
;l=x,y,z。
(13)
利用式(13)计算λ(rc)之后,通过线性插值计算细网格上的λ(rf),则由式(12)可得单元rf中心处的异常场为
Ea(rf)≈λ(rf)·|Eb(rf)|。
(14)
而总场由式(3)给出,最后利用式(2)可计算观测点处的电磁场[16-19]。
2 模型试验和结果分析
2.1 精度验证
针对Newman等[20]给出的三维航空电磁模型,我们将本文算法的结果与其给出的全积分方程结果进行对比,以验证MGQL算法的精确性。模型如图1所示,粗网格剖分数为2×10×10(x×y×z,下同)个,细网格剖分数为4×10×20个。 测线沿着x方向,发射频率为900 Hz,系统飞行高度20 m。三维异常体的几何参数和埋深如图1所示。
图2a、b给出利用本文算法和Newman文中 IE计算的电磁响应对比结果,可见MGQL的磁场Hx、Hz实虚分量曲线与Newman的结果吻合很好。图2c、d给出的相对误差均保持在5%以内,说明本文算法具有很高的精度。
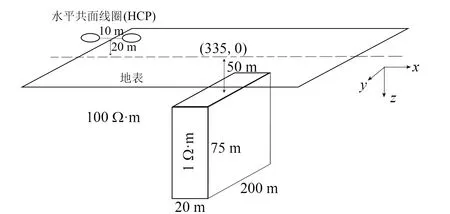
据文献[20]。图1 三维正演模型Fig.1 Models for 3D modeling
2.2 单个异常体模型
航空电磁勘探在地形条件比较复杂的区域应用较多,目标体上方的覆盖层会对异常响应产生影响[21-22]。因此,本节采用的模型与图1类似,只是在地表加一层电阻率为10 Ω·m、厚度为10 m覆盖层,异常体为30 m×180 m×70 m, 电阻率为1 Ω·m,埋深40 m,粗网格剖分网格数为2×10×10个,细网格剖分网格数为4×10×20个。测线沿x方向,飞行高度30 m,频率900 Hz。

图2 MGQL算法与Newman IE(1995)正演结果对比Fig.2 Comparison of MGQL results from this paper with those of Newman (1995)
图3给出含覆盖层与不含覆盖层的单个异常体航空电磁响应对比。由3图可见:覆盖层不影响异常响应曲线形态,但是异常响应幅值发生明显变化,含覆盖层异常体电磁响应明显大于不含覆盖层的电磁响应,说明良导覆盖层增强了异常体的电磁响应(背景值得到提升)。
2.3 多个异常体模型
在三维航空电磁正演计算中,多个异常体之间存在电磁耦合。利用Zhdanov等[14]提出的不均匀背景电导率法(IBC),当存在多个异常体时,对每个异常体使用积分方程进行计算,然后通过耦合迭代求解电磁响应,但这种方法计算速度较慢。本文采用MGQL算法,由于积分是在粗糙网格上进行的,耦合迭代速度极大地提升。这种方法对网格数巨大的模型求解优势更为明显。为验证MGQL算法对多个异常体模拟的有效性,我们设计如图4所示的模型,频率为900 Hz,粗网格剖分数为4×10×10个,细网格剖分数为8×10×20个,测线沿着x方向,飞行高度30 m。
为了方便对比,本文分别计算存在单个异常体和多个异常体时电磁响应。图5a、b给出存在单个异常体时Hx和Hz响应,而图5c、d给出存在两个异常体时Hx和Hz响应曲线。由图5可以看出,由于两个异常体之间存在电磁耦合,单个异常体电磁响应的叠加明显大于两个异常体组合的电磁响应;说明异常体之间的二次耦合不可忽视。
3 计算效率分析
本文提出的MGQL算法的最大优点是在保证计算精度的前提下达到快速计算的目标。为了分析MGQL算法的计算效率,本文将其与开源软件MarcoAir (Version 2.3.1)及全积分方程算法结果作对比。本文设计与图1类似的模型,异常体大小为30 m×200 m×100 m,电阻率1 Ω·m,埋深30 m,飞行高度30 m, 频率900 Hz,测线沿x方向。通常,全矩阵存储积分方程法需要占用大量的内存空间,用于存储格林系数矩阵。受内存限制,全矩阵存储积分方程法计算网格数有限。使用MGQL技术能够减少网格数、节约存储,可实现多网格数剖分的正演模拟。本文的计算在Intel(R) Xeon(R) CPU E5-2667 v3@3.20 Hz处理器上进行,内存128 GB,操作系统为64位Win7系统。
MarcoAir属于早期研发的积分方程算法,它利用格林函数的对称性和块迭代算法提升积分方程的计算速度[22]。当异常体剖分单元较少时,直接解法优势较大;当剖分单元较多时,迭代法计算速度较快。我们对比时选用MarcoAir迭代法求解线性方程组。本文MGQL算法中将格林函数存储为Toeplitz矩阵形式,同时利用FFT实现矩阵与向量乘积,并采用稳定双共轭梯度法(BICGSTAB)求解线性方程组[23-24],以进一步加快计算速度。假设航空电磁系统发射源和接收机共移动60次。表1给出在相同计算精度条件下,本文算法计算时间与MarcoAir的对比结果。由表1可见:当网格数较少时,MarcoAir求解速度快于MGQL算法;随着模型剖分网格数增加,MGQL算法计算速度远远超过MarcoAir。例如,当网格数增加到10×20×20时,MGQL的计算速度是MarcoAir近54倍。另外,对于计算设备的有限存储空间和时间,MarcoAir可以计算的网格数不超过20×40×40个,而对于MGQL算法来说,可以计算的网格数为50×100×100。由于MGQL在粗网格上求解异常场,计算量极大减少,使得该算法在计算效率上拥有很大的优势。
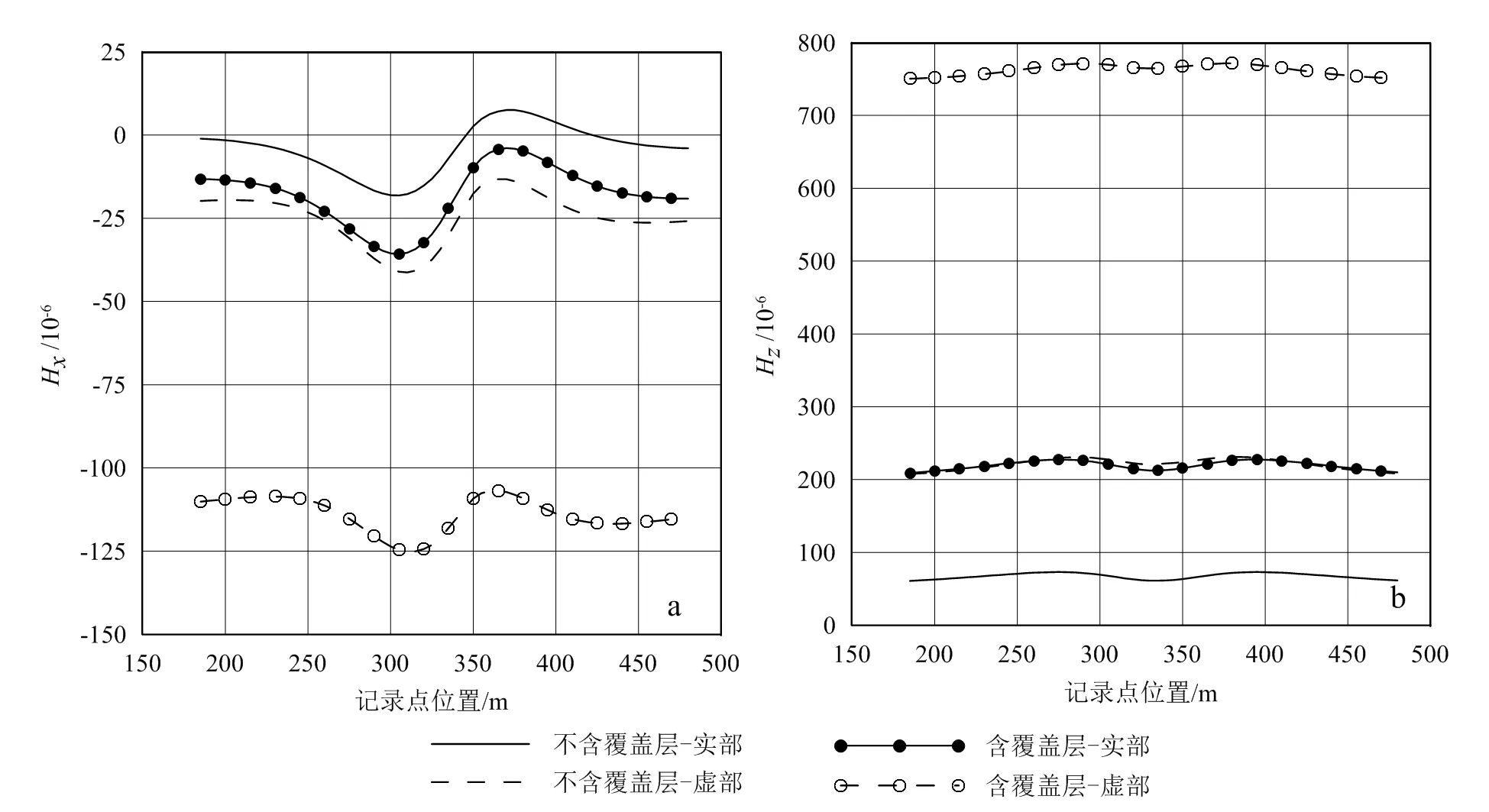
图3 不含覆盖层和含覆盖层单个异常体航空电磁响应Fig.3 AEM responses for an anomalous body in a homogeneous earth with and without overburden

图4 多个异常体三维正演模型Fig.4 Multiple anomalous bodies for 3D modeling
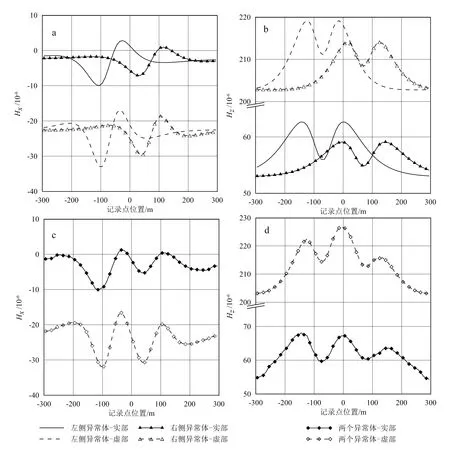
a,b.单个异常体存在时;c,d.多个异常体存在时。图5 单个异常体和多个异常体的航空电磁响应对比Fig.5 Comparison of AEM responses for single anomalous body and multiple anomalous bodies
表1MGQL和MarcoAir不同网格剖分的计算时间对比
Table1ComputationtimeforMGQLandMarcoAirfordifferentgrids

Nx×Ny×NztMGQL/mintMarcoAir/min5×5×50.020.015×10×100.110.5610×20×201.3775.6120×40×4022.36****30×60×60112.38****50×100×1001318.17****100×100×100********
注:N为网格数;t为计算时间;*|*|*|*表示计算时间大于24 h。
对于表1设计的模型,我们进一步在MGQL与全积分方程法(全矩阵存储和直接矩阵向量乘积算法)之间进行计算效率对比,结果如图6所示。对比结果表明,MGQL算法明显具有计算速度快、占用内存少的优势。随着剖分网格增加,全积分方程计算时间和占用内存呈指数增加;但对MGQL算法,随网格数增加,其计算时间和占用内存增长缓慢,凸显出MGQL算法的高效性。

图6 MGQL算法与全积分方程法计算时间和占用内存对比Fig.6 Comparison of MGQL with classic IE from calculation time and memory requirement
下面说明MGQL算法如何通过粗细网格结合,实现航空电磁响应高效三维数值模拟。采用的模型与表1相同,航空电磁系统发射源和接收机共移动60次,异常体离散为2×10×10个粗网格和4×10×20个细网格。我们分别采用如下3种方法:1)在粗网格上应用积分方程法(BICGSTAB-FFT);2)在精细网格上应用积分方程法;3)在粗细多重网格上应用MGQL算法。图7是3种方法的计算的Hz响应对比。由7图可以看出:方法1)的结果与方法3)的计算结果差距较大,而方法2)和3)的响应曲线吻合度高。3种方法的计算时间分别为13.12、69.61和16.06 s。很显然,本文算法在保证计算精度的同时,大大提升了航空电磁数据正演模拟的计算效率。
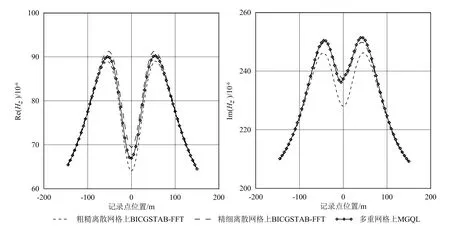
图7 3种方法计算的Hz响应对比Fig.7 Comparison of Hz responses calculated by three methods
4 结论
本文提出的MGQL算法有效地解决了积分方程计算时占用内存大、计算速度慢的问题。通过移动场源航空电磁三维模型试验,并与已发表的算法结果对比,表明响应误差均小于5%。另外本文算法模拟多个异常体也取得很好的结果,说明MGQL算法在满足精度要求的条件下能够求解大型复杂异常体模型,是解决多源航空电磁问题的有效算法。
在相同模型保证计算精度的前提下,本文算法相比于MarcoAir算法和全积分方程法,网格数越多,相对计算时间越少、占用存储越小,说明利用矩阵Toeplitz性质和BICGSTAB-FFT有效地提升了计算效率。探究精算精度与网格的关系发现,采用组合网格可以使用最小的内存和计算时间获得高的计算精度。因此,未来我们将尝试利用MGQL算法进行多源航空电磁数据的快速成像和反演。
致谢: 感谢开源软件MarcoAir的作者,感谢吉林大学 “千人计划”电磁研究团队全体成员。
[1] 殷长春,张博,刘云鹤,等.航空电磁勘查技术发展现状及展望[J].地球物理学报,2015,58(8): 2637-2653.
Yin Changchun,Zhang Bo,Liu Yunhe,et al. Review on Airborne EM Technology and Developments [J]. Chinese Journal Geophysics,2015,58(8): 2637-2653.
[2]Habashy T M,Groom R W,Spies B R. Beyond the Born and Rytov Approximations: A Nonlinear Approach to Electromagnetic Scattering [J]. J Geophys Res,1993,98(B2): 1759-1775.
[3] Zhdanov M S,Fang S. Quasi-Linear Approximation in 3-D Electromagnetic Modeling [J]. Geophysics,1996,61(3): 646-665.
[4] Zhdanov M S,Fang S. Quasi-Linear Series in Three-Dimensional Electromagnetic Modeling [J]. Radio Science,1997,32(6): 2167-2188.
[5]Zhdanov M S,Dmitriev V I,Fang S,et al. Quasi-Analytical Approximations and Series in 3D Electromagnetic Modeling [J]. Geophysics,2000,65(6): 1746-1757.
[6] Zhdanov M S,Tartaras E. Three-Dimensional Inver-sion of Multitransmitter Electromagnetic Data Based on the Localized Quasi-Linear Approximation [J]. Geophys J Int,2002,148 (3): 506-519.
[7] 刘永亮,李桐林,胡英才,等. 快速拟线性近似方法及三维频谱激电反演研究[J]. 地球物理学报,2015,58(12): 4709-4717.
Liu Yongliang,Li Tonglin,Hu Yingcai,et al. Fast Quasi-Linear Approximation and the Three-Dimensional Spectrum of Induced Polarization Inversion Study [J]. Chinese Journal Geophysics,2015,58(12): 4709-4717.
[8]Ueda T,Zhdanov M S. Fast Numerical Modeling of Multitransmitter Electromagnetic Data Using Multigrid Quasi-Linear Approximation [J]. IEEE Transactions on Geoscience and Remote Sensing,2006,44(6): 1428-1434.
[9] 周后型.大型电磁问题快速算法的研究[D].南京:东南大学,2002.
Zhou Houxing. Inverstigations on Fast Algorithms for Electrically Large Eletromagnetic Problems [D]. Nanjing: Southeast University, 2002.
[10] Zhang Z Q,Liu Q H. Three-Dimensional Weak-Form Conjugate- and Biconjugate-Gradient FFT Methods for Volume Integral Equations [J]. Microwave and Optical Technology Letters,2001,29(5): 350-356.
[11] Hohmann G W. Three-Dimesional Induced Polariza-tion and Electromagnetic Modeling [J]. Geophysics,1975,40(2): 309-324.
[12]Wannamaker P E,Hohmann G W,Sanfilipo W A. Electromagnetic Modeling of Three-Dimensional Using Integral Equations [J]. Geophysics,1984,49(1): 60-74.
[13] Born M. Optic [M]. New York: Springer,1933.
[14] Zhdanov M S,Lee S K,Yoshioka K. Integral Equation Method for 3D Modeling of Electromagnetic Fields in Complex Structures with Inhomogeneous Background Conductivity [J]. Geophysics,2006,71(6): G333-G345.
[15] Gao G Z,Torres-Verdin C,Fang S. Fast 3D Modeling of Borehole Induction Measurements in Dipping and Anisotropic Formations Using a Novel Approximation Technique [J]. Petrophysics,2004,45(4): 335-349.
[16] 张金会,孙建国. 三维直流电场积分方程中奇异性的近似处理[J]. 吉林大学学报(地球科学版),2009,39(5): 923-928.
Zhang Jinhui,Sun Jianguo. Treatment of Singularity in Integration Equations for 3D DC Electrical Field [J]. Journal of Jilin University (Earth Science Edition),2009,39(5): 923-928.
[17] Xiong Z. Electromagnetic Fields of Electric Dipoles Embedded in a Stratified Anisotropic Earth [J]. Geophysics,1989,54(12): 1643-1646.
[18] Xiong Z. Electromagnetic Modeling of 3-D Structures by the Method of System Iteration Using Integral Equations [J]. Geophysics,1992,57(12): 1556-1561.
[19] 张辉,李桐林,董瑞霞. 基于电偶源的体积分方程法三维电磁反演[J]. 吉林大学学报(地球科学版),2006,36(2): 284-288.
Zhang Hui,Li Tonglin,Dong Ruixia. 3D Electromagnetic Inversion by Volume Integral Equation Method Based on Current Dipole Source [J]. Journal of Jilin University (Earth Science Edition),2006,36(2): 284-288.
[20] Newman G A,Alumbaugh D L. Frequency-Domain Modeling of Airborne Electromagnetic Responses Using Staggered Finite Differences [J]. Geophysical Prospecting,1995,43: 1021-1042.
[21] 黄威,殷长春,贲放,等. 频率域航空电磁三维矢量有限元正演模拟[J]. 地球科学,2016,41(2): 331-342.
Huang Wei,Yin Changchun,Ben Fang,et al. 3D Forward Modeling for Frequency AEM by Vector Finite Element [J]. Earth Science,2016,41(2): 331-342.
[22] 张博,殷长春,刘云鹤,等. 起伏地表频率域/时域航空电磁系统三维正演模拟研究[J]. 地球物理学报,2016,59(4): 1506-1520.
Zhang Bo,Yin Changchun,Liu Yunhe,et al. 3D Modeling on Topographic Effect for Frequency-/Time-Domain Airborne EM Systems [J].Chinese Journal Geophysics,2016,59(4): 1506-1520.
[23] 王德智.基于积分方程技术的三维电磁法正演模拟研究[D].长春:吉林大学,2015.
Wang Dezhi. Three-Dimensional EM Forward Modeling Based on Integral Equation Method [D]. Changchun: Jilin University,2015.
[24] Chew W C,Tong M S,Hu B. Integral Equation Me-thods for Electromagnetic and Elastic Waves [M]. San Rafeal: Morgan & Claypool Publishers,2009.

