四旋翼无人机一致性编队飞行控制方法
陈杰敏+吴发林+耿澄浩+徐珊


摘 要: 四旋翼无人机在民用及军用领域都发挥着越来越重要的作用。 为了完成某些特定任务, 需要由多架四旋翼组成的编队保持适当队形飞行。 与单架四旋翼执行任务相比, 四旋翼编队具有能增加任务成功率、 提高整体抗干扰性能、 扩大监控范围等优点。 本文基于主从式编队结构, 结合信息拓扑理论, 把四旋翼编队描述为二阶一致性系统, 设计编队控制器来实现四旋翼编队的稳定飞行。 主机和从机均采用PID控制, 主机跟踪预设轨迹, 从机跟踪编队控制器计算出的轨迹跟踪指令。 最后通过仿真分析了控制算法对四旋翼编队队形生成及队形保持的控制效果。
關键词: 四旋翼无人机; 编队飞行; 信息拓扑理论; 一致性理论; 主从式编队
中图分类号: V249.1 文献标识码: A 文章编号: 1673-5048(2017)06-0025-07[SQ0]
0 引 言
四旋翼无人机(以下简称四旋翼)是一种有四个螺旋桨且螺旋桨分别呈十字交叉型的飞行器。 在过去的数十年中, 传感器及电子元器件的微型化、 低廉化推动了四旋翼的快速发展。 四旋翼在军事领域可用于巡逻侦察、 定点攻击等方面, 在民用领域可用于遥感测绘、 农业植保、 通信中继、 航拍航测、 短途运输等方面, 具有广泛的应用前景和实际用途, 成为商业公司和科研单位的研究热点[1]。 随着无线传感网络等技术的创新应用, 由多架无人机组成的编队在民用及军事等方面都展现出越来越广泛的用途, 如能进行空中集群表演、 组建军事通信网络、 构建网络化军事打击编队等。
无人机编队飞行, 是指在三维空间中, 多架无人机按照一定的队形进行排列, 使其在飞行过程中保持队形不变或者相对位置在一定范围内变动, 并能根据外部情况和任务需求进行动态调整, 以保持编队的协同一致性。
无人机编队飞行控制方式主要有主从法[2]、 虚拟结构法[3-4]、 行为控制法[5-6]等。 主从法结构中, 其中一个飞行器被指定为主机, 其余飞行器则被指定为从机。 从机以一定的偏移量跟踪主机的方向及位置。 虚拟结构法把整个编队视为单一的虚拟结构, 每架无人机是虚拟结构中相对位置固定的一点。 当编队移动时, 每架无人机跟踪队形中固定点的运动即可。 行为控制法是将主要控制目标分解为一些预期行为, 并基于控制输入的加权平均为每一个行为设计单独的控制输入, 能处理诸如队形保持、 碰撞规避、 中心聚拢等行为。
多智能体集群行为可定义为:集群系统中的多智能体通过局部信息相互作用, 并遵循三条原则:(1) 避免群体成员之间的碰撞;(2) 智能体与其邻居的速度尽量匹配;(3) 各智能体尽量向邻居智能体靠近, 并保持一定的群聚性。 多无人机编队飞行也属于多智能系统的研究范畴, 基于该理论研究无人机编队飞行系统是近年来的研究热点, 特别是对信息拓扑理论思想的运用, 将编队系统看成是通信与感知信息流构成的通信拓扑, 利用一致性问题的研究方法进行研究, 得到了许多学者的青睐。 控制器的设计与系统性能分析可利用编队飞行器间的信息交互数学模型, 按照代数图论的方法进行研究。 如薛瑞彬等[7]考虑编队系统存在通讯时延的情况下, 利用一致性理论设计了分布式编队控制算法, 并对系统稳定性予以理论和仿真证明。 周稼康等[8]针对主从结构的编队飞行系统, 基于一致性算法分析了通信拓扑结构为有向图时系统控制器参数的选取。 文献[9-10]研究了基于一致性理论的无人机时变编队的控制算法, 并在四旋翼硬件平台上进行了验证。 文献[11]将存在多个时延的线性时变拓扑结构转化为一致性问题进行研究分析, 并将结果用于编队飞行系统的研究中。
为改进传统主从飞行编队信息交流单一的不足, 本文将信息拓扑理论应用于无人机主从编队, 增加从机与从机之间的信息交互, 从而使编队在飞行过程中队形保持更加稳定, 且队形变换更加多样。
1 四旋翼模型建立
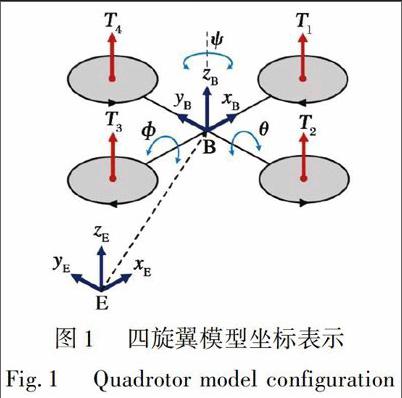
在大地坐标系E及载体坐标系B下建立四旋翼模型。 四旋翼模型坐标表示如图1所示。 四旋翼质量为m, 对应的转动惯量矩阵I。 位置及姿态角分别记为r=[xyz]T和η=[θψ]T。 在载体坐标系B下定义角速度ω=[pqr]T。
为了简化控制方案设计, 根据以下假设, 对四旋翼模型进行合理简化[12]。 首先, 四旋翼为对称刚体, 其质心与载体坐标系原点重合, 转动惯量矩阵简化为I=diag[IxxIyyIzz]。 其次, 四旋翼工作在悬浮状态, 其横滚角及俯仰角θ均较小[13](c≈1, cθ≈1, s≈, sθ≈θ), 因此, 载体角速度ω可认为与姿态角变化率相等, 并且忽略陀螺力矩。
根据牛顿欧拉法, 四旋翼平移动力学及旋转动力学方程如下:
式中: g为重力加速度; ez=[001]T为大地坐标系下的单位向量; TB为载体坐标系下四个旋翼产生的总推力; REB∈SO(3)为从载体坐标系B向大地坐标系E变换的旋转矩阵; τ为作用在四旋翼上的控制力矩。 τ和TB组成系统的4个输入u, 通过改变τ和TB来改变旋翼的转速, 从而控制四旋翼向期望位置运动。 旋转矩阵RBE、 4个旋翼的转速与τ和TB的变换关系分别如式(3)~(4)所示:
2 四旋翼控制
为了更好地验证编队控制器性能, 底层四旋翼控制采用成熟的PID控制算法, 内环控制姿态, 外环控制位置, 控制框图见图2。
3 编队控制
3.1 信息拓扑理论
为了实现垂直起降无人机群的编队飞行或者保证刚体姿态同步, 必须利用局部信息交换来设计控制方案。 因此, 无人机之间需要发送状态信息。 本文用加权图来描述组成员之间的信息交换。 在此给出信息拓扑理论的一些标准定义和特性。
加权图G由三元组(V, E, A)组成, 其中V={v1, v2, ..., vn}是节点或顶点集合, 用于描述集群中飞行器集合。 EV×V是成对节点的集合, 称为边。 A=[aij]∈Rn×n是加权邻接矩阵。 边(i, j)∈E表示第i个系统接收来自第j个系统的信息, 且j与i相邻。 通常, 在图中利用从节点vj指向节点vi的有向线段, 表示后者能够直接获取前者的信息, 并称vi是vj的父节点, vj是vi的子节点。 若vi与vj之间可相互获取信息, 则两者互为父子节点, 满足(vi, vj)∈E(vj, vi)∈E, 且两者之间的有向线段为双向, 称为双向边, 一般用双向箭头线段或者不带箭头的线段表示。 若G中所有的边均为双向边, 则G为无向图, 可视为有向图的特例。
加权图的加权邻接矩阵定义:当且仅当(i, j)∈E时, aij>0;当且仅当(i, j)E时, aij=0。 如果系统间的互连是双向的, 那么加权图G是无向的, E中的节点对是无序的, 即(i, j)∈E(j, i)∈E, 且A是对称的, 即aij=aji。 在单向互连接的情况下, G是一个有向图, E包含有序节点对, A不一定是对称的。 在信息拓扑理论中, 有向边(i, j)用一个由节点j指向节点i的有向连接线(箭头)来表示。 在无向图中, 使用没有箭头的连接线。
如果有向圖中任意两个完全不同节点之间存在一条有向路径, 则该图称为是强连通的。 这里, 有向路径是有向图中的有向边序列, 其形式是(i1, i2), (i2, i3), …, 其中il∈V。 记任意节点vi的邻居集为Ni(G)=j∈V(G)(i, j)∈E(G), 若流入节点vi的信息个数等于其流向其他所有节点的个数, 即节点vi的入度degini=∑i∈Njaij与出度degouti=∑j∈Niaij相等时, 称图G是平衡的。 显然, 任意无向图是平衡的。 若A中的非零元素均为1, 对于任意节点vi, 有∑nj=1aij=∑nj=1aji成立, 显然图G是平衡的, 此时称G为不加权图。 如果用无向边替代(有向图G中的)有向边而获得的无向图G'是连通的, 那么称有向图G是弱连通的。 更多关于信息拓扑理论的介绍及有关图论的例子请参考文献[14]。
利用拓扑结构中的边来表示无人机的通信或控制链路, 双向边则可用于表示两架无人机间可双向进行交互。 由于编队系统中的任意无人机均可能对这个系统产生影响, 故而可利用信息将其拓扑为无向连通图或者有向强连通图, 但编队飞行的无人机之间获取相互信息的能力不同, 相互之间不一定能够获取彼此信息, 故而信息交互可能是单向的, 特别是在主从结构的编队飞行中, 其信息拓扑一般为有向图。
3.2 一致性编队理论
一致性理论是根据多智能体间的状态信息流通, 按照网络拓扑的思想构造一致性算法, 使得智能体与邻居智能体的状态误差保持一致, 并使得多智能体的状态信息与期望信息保持一致。 利用一致性理论对编队系统协同控制问题进行研究, 可归纳为将编队系统转化为网络拓扑结构, 通过一致性算法使得无人机的状态信息与期望信息保持一致, 从而实现多无人机自主编队运动控制。
对一致性理论分布式编队飞行控制的研究, 常采用二阶一致性算法进行分析。
设双积分连续系统为
式中: i=1, 2, …, n, 其中n为系统中多智能体个数; xi∈Rm, vi∈Rm分别为第i个智能体的位置和速度矢量。 式(17)的一致性问题可归纳为给定任意系统初始值xi(0), vi(0)与i=1, 2, …, n, 设计控制器ui, 使当t→∞时, |xi-xj|→0, (i, j=1, 2, …, n)和|vi-vj|→0, (i, j=1, 2, …, n)成立。 解决该问题的方法是设计如下二阶一致性算法[15]:
式中: β>0, aij为加权邻接矩阵A中第i行第j列元素。
3.3 多四旋翼一致性编队飞行控制方案
由N架四旋翼组成编队, 根据其之间的信息通信关系, 把飞行编队建模为有向图G, 有向图节点vi表示第i架四旋翼。 信息流通方向由有向图G中的箭头方向表示。 节点v1表示主机, 其余节点表示从机。 主机把自身的状态发送给从机, 从机之间信息拓扑关系可为任意有向图。
四旋翼编队生成问题描述为各无人机在零时刻静止于地面且无队形, 设计拓扑结构G, 并根据主机的位姿信息设计从机vi的期望跟踪指令, 使得ri-rd→0, ψi-ψd→0, 下标d表示对应的期望值。
在主从编队模式中, 主机位置为编队一致性算法的平衡点。 定义主机与从机的期望位置偏差为相对位置偏差, 记为R*i=[x*i y*i z*i]T。 通过改变通信拓扑结构和设置不同的R*i即可设计出不同的编队形状。
在主从编队模式下, 给出一致性编队算法如下:
式中: xdL和vdL分别为编队主机的位置和速度; α表示主机与从机的邻接关系。 当从机i能接收到主机的状态信息时, α>0, 否则, α=0。 v·dL为主机的加速度信息。
因此, 四旋翼一致性编队飞行控制方法的计算步骤如下:
(1)根据编队中无人机之间的通信关系, 设计编队信息拓扑结构。 信息拓扑结构决定了对应的邻接矩阵。
(2)根据飞行编队的期望队形, 设计相对位置偏差矩阵R*i=[x*i y*i z*i]T。
(3)设计主机飞行轨迹, 通过PID控制使主机跟踪期望轨迹飞行。
(4)从机接收主机的位置和速度信息, 以及其他有信息交互的从机的位置和速度, 通过式(19)计算出其下一时刻的加速度, 从而计算出下一时刻的期望位置。
(5)通过计算得到的从机期望位置, 由PID控制器来控制从机, 从而使从机跟踪期望位置飞行。
通过以上步骤, 可以实现四旋翼编队保持期望的队形飞行。
4 仿真与分析
4.1 仿真参数设置
在Matlab/Simulink环境中搭建四旋翼模型, 模拟5架微小型四旋翼在无障碍物环境下的编队飞行。 具体参数为:m=0.58 kg, Ixx=Iyy=0.114 7 kg/m2, Izz=0.052 2 kg/m2。 一致性编队算法中, α=1, β=2, v1为主机, vi(i=2, 3, 4, 5)为从机。 队形为正方形, 主机位于中心, 从机位于正方形四角, 相对位置偏差矩阵设为
5架四旋翼均从原点出发, 4架从机根据一致性编队协议及相对位置偏差, 按照编队控制器计算出的期望位置指令, 向各自的期望点运动。 编队飞行轨迹为上升的S形曲线, 主机期望飞行轨迹曲线方程为x=0.1t, y=20cos(πt/50)-20, z=0.1t。 仿真时间设为200 s, 仿真步长为0.001 s。
4.2 仿真结果分析
图4为四旋翼编队飞行三维轨迹图。 从图中可
以看出, 通过一致性理论编队控制算法来控制编队, 无人机起飞后, 能自主形成期望队形, 并保持稳定队形飞行。 图5为xy平面的飞行轨迹, 可以
的位置。 5架无人机形成预设队形后, 从机能跟随看出, 在初始阶段, 从机能自主飞往各自期望
保持相对队形不变协同飞行。 图6为5架无人机在z方向的位置变化图, 可以看出在2.5 s后, 从机与主机的高度收敛为一致。
以从机1为例, 分析从机的飞行轨迹。 图7表示从机1的编队控制器根据式(18)计算出的u随时间的变化, 再根据u计算从机1的期望跟踪位
置。 图8中表示从机1的实际位置和姿态角随时间的变化。 可以看出, 其位置能跟踪期望位置指令飞行, 其三维姿态角在0.5 s左右即可达到小角度飞行的稳定状态。 分析其位置误差, 如图9所示, 相
对位置偏差R*1=[50 0]T, 所以零时刻x方向与期望位置的误差为5 m, y方向与期望位置的误差为0 m。 从机1启动后, x方向误差从5 m逐渐收敛, 在7 s后收敛为0附近。 y方向
误差从0 m先上升至0.8 m, 在8 s后收敛到0附近。 通过分析可得, 本文中采取的一致性算法能起到
较好的误差收敛效果。 其他从机的相关误差特性与从机1类似, 不再赘述。
5 结 论
本文采用二阶一致性理论及信息拓扑理论设计微小型四旋翼主从式编队控制算法, 编队中的单架四旋翼控制采用PID控制器。 通过Matlab/Simulink仿真验证了该算法的有效性。 在本文中的算法暂未考虑通信时延、 外部噪声扰动等不确定性因素, 下一阶段将以上因素考虑在模型内, 以提高该算法在实际工程应用中的价值。
参考文献:
[1] Floreano D, Wood R J. Science, Technology and the Future of Small Autonomous Drones[J]. Nature, 2015, 521(7553): 460-466.
[2] Roldo V, Cunha R, Cabecinhas D, et al. A Leader-Following Trajectory Generator with Application to Quadrotor Formation Flight[J]. Robotics & Autonomous Systems, 2014, 62(10): 1597-1609.
[3] Davidi A, Berman N, Arogeti S. Formation Flight Using Multiple Integral Backstepping Controllers[C]∥ IEEE 5th International Conference on Cybernetics and Intelligent Systems (CIS), 2011: 317-322.
[4] Ren W, Beard R. Decentralized Scheme for Spacecraft Formation Flying via the Virtual Structure Approach[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(1): 73-82.
[5] Balch T, Arkin R C. Behavior-Based Formation Control for Multirobot Teams[J]. IEEE Transactions on Robotics and Automation, 1998, 14(6): 926-939.
[6] Xu Dongdong, Zhang Xingnan, Zhu Zhangqing, et al. Behavior-Based Formation Control of Swarm Robots[J]. Mathematical Problems in Engineering, 2014(1): 1214-1225.
[7] 薛瑞彬, 宋建梅, 張民强. 具有时延及联合连通拓扑的多飞行器分布式协同编队飞行控制研究[J]. 兵工学报, 2015, 36(3): 492-502.
Xue Ruibin, Song Jianmei, Zhang Minqiang. Research on Distributed Multi-Vehicle Coordinated Formation Flight Control With Coupling Tine-Delay and Jointy-Connected Topologiex[J]. Acta Armamentarii, 2015, 36(3): 492-502.(in Chinese)
[8] 周稼康, 胡庆雷, 马广富, 等. 基于一致性算法的卫星编队姿轨耦合的协同控制[J]. 系统工程与电子技术, 2011, 33(4): 825-832.
Zhou Jiakang, Hu Qinglei, Ma Guangfu, et al. Cooperative Attitude and Translation Controll of Satellite Formation Flying Using Consensus Algorithrn[J]. Systems Engineering and Electroniscs, 2011, 33(4): 825-832.
(in Chinese)
[9] Dong Xiwang, Yu Bocheng, Shi Zongying, et al. Time-Varying Formation Control for Unmanned Aerial Vehicles: Theories and Applications[J]. IEEE Transactions on Control Systems Technology, 2014, 23(1): 340-348.
[10] Yu Bocheng, Dong Xiwang, Shi Zongying, et al. Formation Control for Quadrotor Swarm Systems: Algorithms and Experiments[C]∥32nd Chinese Control Conference (CCC), 2013: 7099-7104.
[11] Yang Xiaogang, Xi Jianxiang, Wu Jinying, et al. Consensus Transformation for Multi-Agent Systems with Topology Variances and Time-Varying Delays[J]. Neurocomputing, 2015, 168: 1059-1064.
[12] Mohd Basri M A, Husain A R, Danapalasingam K A. Stabilization and Trajectory Tracking Control for Underactuated Quadrotor Helicopter Subject to Wind-Gust Disturbance[J]. Sadhana, 2015, 40(5): 1531-1553.
[13] Mellinger D W. Trajectory Generation and Control for Quadrotors[D]. Philadelphia: University of Pennsylvania, 2012.
[14] Jungnickel D. Graphs, Networks and Algorithms[M]. Springer, 2005.
[15] Ren W, Atkins E. Distributed Multi-Vehicle Coordinated Control via Local Information Exchange[J]. International Journal of Robust and Nonlinear Control, 2007, 17(10-11): 1002-1033.
Consensus-Based Formation Control Approach for Quadrotor UAVs
Chen Jiemin, Wu Falin, Geng Chenghao, Xu Shan
(School of Instrumentation Science and Opto-Electronics Engineering, Beihang University, Beijing 100191, China) Abstract: Quadrotors are playing an important role in numerous civilian and military applications. In many applications, a team of quadrotors needs to execute a mission while maintaining a specific shape. Compared with conventional system, formation flight can improve the probability of success, increase the anti-interference performance and expand the region of surveillance. In this paper, the quadrotor formation is described as a second-order consensus system based on leader-follower structure and information topology theory, in order to design a formation controller for steady formation flight. The leader and the follower quadrotors are controlled by PID laws. The leader follows the desired trajectory while the followers follow the instruction calculated by the formation controller. A simulation is carried out to analyze the control effect of formation gathering and keeping of quadrotors with control algorithm.
Key words: quadrotor UAVs; formation flight; information topology theory; consensus-based theory; leader-follower formation

