计及感应电动机参数的微电网暂态电压稳定性分析

李润泽 徐 涛

暂态电压稳定指电力系统短期内遭受大扰动后系统保持稳定电压的能力，同样微电网受到大扰动后，也会出现暂态电压失稳现象，严重情况下会致使微电网系统崩溃。大扰动经常由短路故障造成，而扰动过后感应电动机负荷电压是否稳定，决定着微电网电压稳定性，系统中超过60%负荷是由感应电动机构成[1]，暂态电压失稳与感应电动机负荷密切相关。

文献[2]将临界故障清除时间作为暂态电压稳定的判据，并在多节点系统中验证了其有效性。文献[3]提出了一种计算暂态电压稳定临界故障清除时间的方法，通过Matlab仿真验证了其准确性。文献[4]利用拉格朗日因子法，通过计算推理出一种新的电压稳定判据。文献[5]分析了静态负荷与动态负荷不同比例时的电压稳定性，动态负荷比例越大时电压稳定性越差。文献[6]研究了不同条件下多感应电动机起动对微电网电压稳定性影响。然而在微电网系统中，感应电动机参数变化特性对微电网系统暂态电压稳定性影响的研究较少，本文基于风光储微电网系统，通过改变感应电动机参数研究其在各种条件下的暂态电压稳定性。

1 微电网结构与电压稳定控制策略

1.1 微电网结构

微电网主构架为 10kW 双馈风力发电系统、10kW光伏发电系统、20kVA储能系统、10kW感应电动机负荷和 10kW静态负荷的动态微电网仿真模型，如图 1所示。联网运行时公共连接点（PCC）闭合，各设备经变压器连接到主网。当主网或微电网发生故障时，切掉 PCC，由分布式电源（DG）、储能和负荷独立运行。

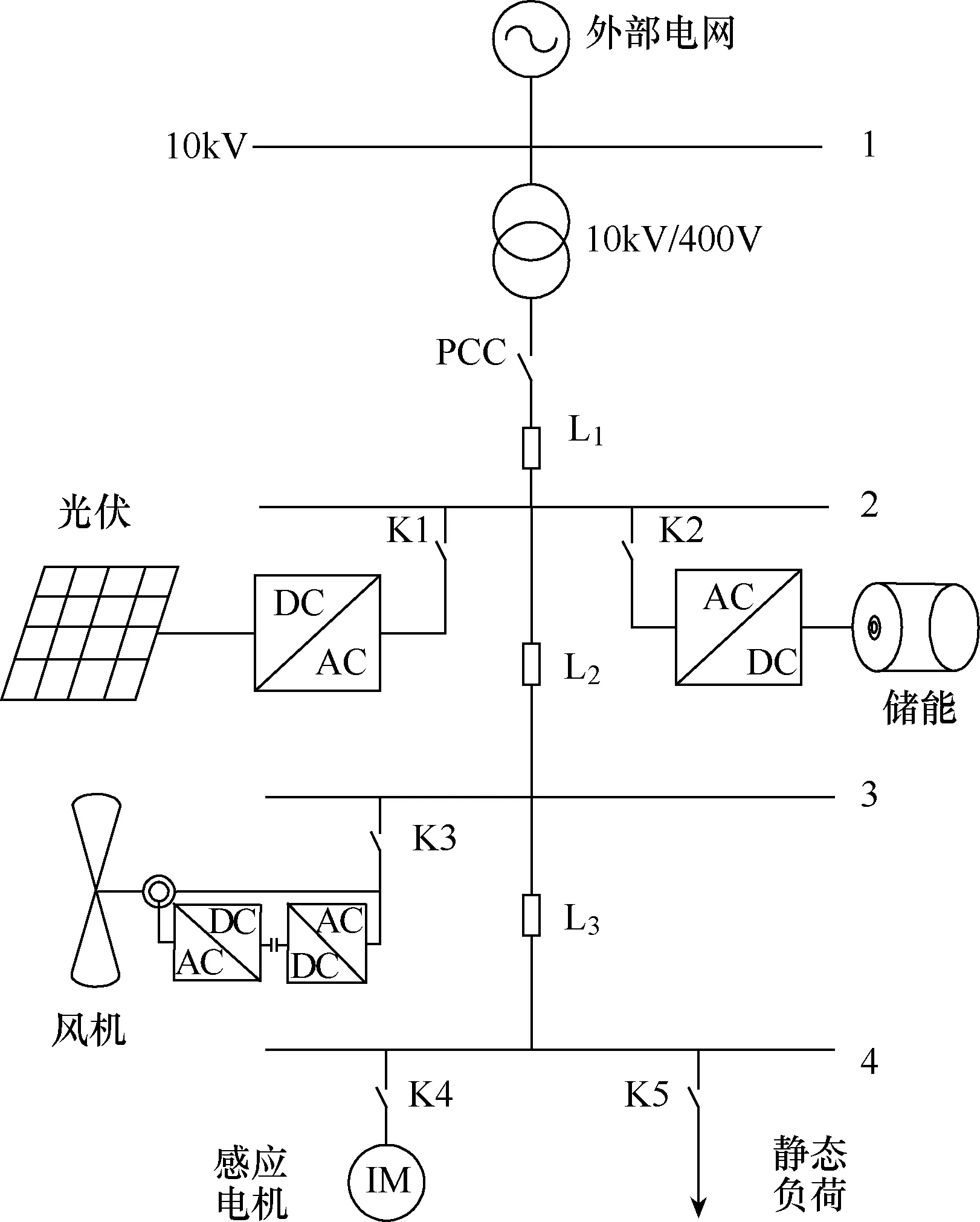
图1 微电网结构图

1.2 电压稳定控制策略

当微电网联网运行时，储能与 DG均采用恒功率控制（PQ）控制方式。当线路L2处发生三相短路故障时，微电网立即转为孤网运行状态，PCC处于断开状态，此时与主网为分离关系，储能则起到稳定系统电压的作用，及时弥补系统电压缺额，控制方式由恒功率控制转为V/F控制，其他DG则继续采用PQ控制方式。储能孤网运行时V/F控制策略如图2所示。

图2 储能V/F控制策略结构图

频率f与参考频率fref比较，经PI调节器输出有功参考 Pref；电压 U与参考电压 Uref比较调制出无功参考 Qref，再经电流环控制生成信号 idref、iqref，通过改变有功和无功参考值使系统电压维持稳定。

双馈风力发电机机侧变流器采用 PQ的控制策略，而网侧变流器采用电流内环电压外环的控制策略。光伏阵列逆变器控制部分采用和风力发电系统机侧变流器部分一样的 PQ控制策略。储能以恒定功率运行，当微电源供给功率过剩时，吸收功率；当功率不能满足负荷的供应时，输出功率。PQ控制结构如图3所示。

图3 PQ控制结构图

图3 中，Pref、Qref分别为有功和无功参考量，idref、iqref分别为d轴和 q轴参考电流。功率外环通过PI控制器调节输出参考指令idref、iqref，经电流内环 PI控制器调节输出电压解耦项 vd1、vq1，再与电压补偿项比较得到指令 vd、vq，最后经矢量坐标变换后对逆变器进行控制，进而得到理想触发脉冲。

2 感应电动机负荷模型

2.1 感应电动机数学模型

感应电动机负荷采用三阶机电暂态模型，即

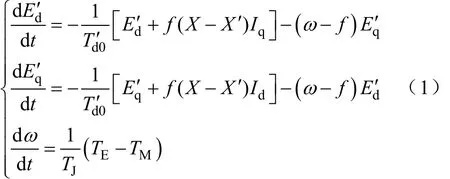
电压方程为

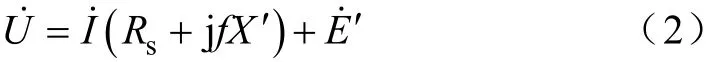
式（1）和式（2）中可描述为

式中， Ed′、 Eq′分别为 d、q轴的暂态电势， Td′0=，I、I分别为定子电流的d、q轴的分量，

dqTd′0为转子绕组时间常数，X、X′分别为稳态与暂态电抗，ω为转子角速度，Xm为激磁电抗，Xs为定子电抗，Xr为转子电抗，TJ为惯性时间常数。

2.2 暂态电压稳定判据

文献[7-8]认为感应电动机电压失稳不一定致使系统电压失稳，系统电压失稳取决于感应电动机失稳后系统电压的稳定情况。文献[3]与文献[9]认为感应电动机电压失稳即为系统电压失稳。据此可知，感应电动机电压失稳是分析系统电压失稳的重要判据，本文微电网暂态电压失稳判据为感应电动机电压失稳。

感应电动机正常运行时，输入电磁功率与输出机械功率保持平衡，电压保持稳定。当微电网在线路L2处受到三相短路故障扰动时，感应电动机电磁功率与机械功率处于非平衡状态，电压处于暂态过程，在短路故障消失后，观察感应电动机电压稳定情况。经过多次仿真，确定感应电动机暂态电压稳定的临界故障清除（CCT）时间为 0.434s，当故障清除时间大于0.434s时，感应电动机电压失稳。图4所示当故障清除时间为0.435s时的感应电动机电压。

图4 感应电动机电压图

3 微电网暂态电压稳定性仿真

3.1 感应电动机参数对微电网暂态电压稳定性影响

1）感应电动机参数选择

选择图1中容量为10kW的单个感应电动机作为仿真主对象，选取感应电动机电压临界时刻感应电动机参数为初始参数。表1所示为感应电动机初始参数。

表1 感应电动机初始参数

3.2 定子电阻对微电网暂态电压稳定性影响

在感应电动机其余参数不变的情况下，改变定子电阻数值，取5组数值且每组数值增加0.02，由表2所示定子电阻在5组数值范围内依次增大时，CCT则相应缩短，变化幅度稳定在4.38%～22.04%之间。由此可知，感应电动机电压稳定性逐渐变差，微电网暂态电压稳定性随着定子电阻的增大而减弱。

表2 感应电动机定子电阻数值与CCT关系

3.3 定子电抗对微电网暂态电压稳定性影响

在感应电动机其余参数不变的情况下，改变定子电抗数值，取5组数值且每组数值增加0.03，由表3所示定子电抗在5组数值范围内依次增大时，CCT则相应缩短，变化幅度稳定在13.29%～17.56%之间。由此可知，感应电动机电压稳定性而逐渐变差，微电网暂态电压稳定性随着定子电抗的增大而减弱。

表3 感应电动机定子电抗数值与CCT关系

3.4 转子电阻对微电网暂态电压稳定性影响

在感应电动机其余参数不变的情况下，改变感应电动机转子电阻数值，取5组数值且每组数值增加0.02，由表4所示转子电阻在五组数值范围内依次增大时，CCT则相应增长，变化幅度稳定在5.88%～10.36%之间。由此可知，感应电动机电压稳定性逐渐变好，微电网暂态电压稳定性随着转子电阻的增大而增强。

3.5 转子电抗对微电网暂态电压稳定性影响

在感应电动机其余参数不变的情况下，改变转子电抗数值，取5组数值且每组数值增加0.02，由表5所示转子电抗在5组数值范围内依次增大时，CCT则相应缩短，变化幅度稳定在6.74%～14.03%之间。由此可知，感应电动机电压稳定性逐渐变差，微电网暂态电压稳定性随着感应电动机转子电抗的增大而减弱。

表4 感应电动机转子电阻数值与CCT关系

表5 感应电动机转子电抗数值与CCT关系

3.6 惯性时间常数对微电网暂态电压稳定性影响

在感应电动机其余参数不变的情况下，改变惯性时间常数，取5组数值且每组数值增加0.05，由表6所示惯性时间常数在五组数值范围内依次增大时，CCT则相应增长，变化幅度稳定在 19.89%～31.80%之间。由此可知，感应电动机电压稳定性逐渐变好，微电网暂态电压稳定性随着感应电动机惯性时间常数的增大而增强。

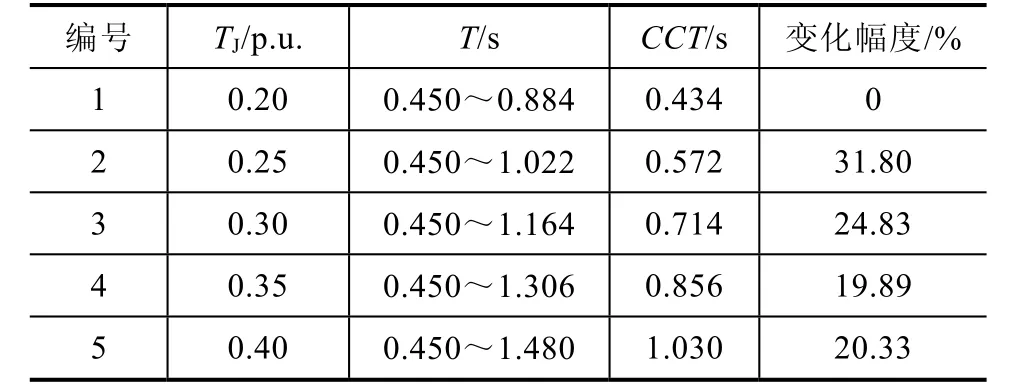
表6 感应电动机惯性时间常数与CCT关系

3.7 负载转矩对微电网暂态电压稳定性影响

在感应电动机其余参数不变的情况下，改变负载转矩，取 5组数值且每组数值增加 0.05，由表7所示，负载转矩在五组数值范围内依次增大时，CCT则相应缩短，变化幅度稳定在 20.66%～27.03%之间。由此可知，感应电动机电压稳定性逐渐变差，微电网暂态电压稳定性随着感应电动机负载转矩增大而减弱。

表7 感应电动机负载转矩与CCT关系

3.8 互感对微电网暂态电压稳定性影响

在感应电动机其他参数不变的情况下，改变感应电动机互感，取5组数值且每组数值增加0.6，由表8所示互感在5组数值范围内依次增大时，CCT则相应缩短，变化幅度稳定在3.815%～6.83%之间。由此可知，感应电动机电压稳定性逐渐变差，微电网暂态电压稳定性随着感应电动机互感增大而减弱。

表8 感应电动机互感与CCT关系

3.9 负荷比例对微电网暂态电压稳定性影响

通过改变感应电动机负荷所占总负荷比例分析微电网暂态电压稳定性，由表9所示随着感应电动机动态负荷比例减小，CCT则相应增长。由此可知，感应电动机电压稳定性逐渐变好，微电网暂态电压稳定性随着感应电动机负荷比例减小而增强。

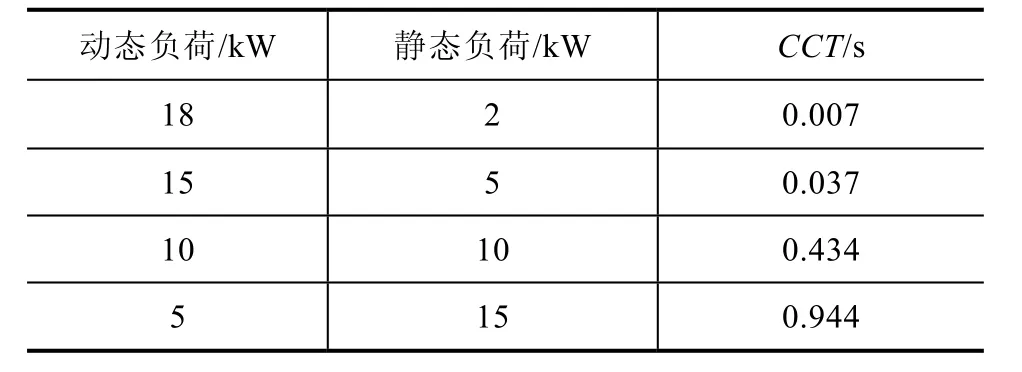
表9 动态与静态负荷比例与CCT关系

4 结论

本文通过构架风光储微电网系统，设计了电压稳定性控制策略，在感应电动机其他参数不变的条件下，改变感应电动机定子、转子、互感、惯性时间常数、负载转矩和负荷比例，利用临界故障清除时间大小来分析微电网在受到短路故障结束后的暂态电压稳定性。结果表明，随着感应电动机定子电阻（0.102～0.182）、定子电抗（0.1317～0.2517）、转子电抗（0.1516～0.2316）、负载转矩（0.60～0.80）、互感（1.394～3.794）和负荷比例（9∶1～1∶3）在其数值范围内逐渐增大，临界故障清除时间相应减小，微电网暂态电压稳定性减弱。随着感应电动机转子电阻（0.100～0.180）和惯性时间常数（0.20～0.40）在其数值范围内逐渐增大，临界故障清除时间相应增大，微电网暂态电压稳定性增强。

[1] 赵兵, 汤涌. 感应电动机负荷的动态特性分析[J].中国电机工程学报, 2009(7)： 71-77.

[2] 李立理, 陆超, 黄志刚. 计及感应电动机的负荷节点暂态电压稳定解析评估方法[J]. 电力系统自动化,2009, 33(7)： 1-5.

[3] 井艳清, 李兴源, 郭晓鸣, 等. 考虑感应电动机负荷模型的暂态电压稳定快速判据[J]. 电力系统自动化,2011, 35(5)： 10-14.

[4] 汤涌, 林伟芳, 孙华东, 等. 考虑负荷变化特性的电压稳定判据分析[J]. 中国电机工程学报, 2010(16)：12-18.

[5] 肖朝霞, 方红伟. 含多分布式电源的微网暂态稳定分析[J]. 电工技术学报, 2011(S1)： 253-261.

[6] 林莉, 朱丽云, 张向伍, 等. 含多感应电动机负荷的微网电压稳定性仿真分析[J]. 电力系统自动化, 2017,41(8)： 78-83.

[7] 李鹏, 余贻鑫, 贾宏杰. 关于更精确的电压稳定极限描述中所需模型与方法的研究[J]. 中国电机工程学报, 2004, 24(10)： 21-26.

[8] Vournas C D, Manos G A. Modelling of stalling motors during voltage stability studies[J]. IEEE Transactions on Power Systems, 1998, 13(3)： 775-781.

[9] 孙华东. 计及感应电动机负荷的电压稳定分析及其应用研究[D]. 北京： 中国电力科学研究院, 2005.

[10] 黄宜平, 马晓轩. 微电网技术综述(英文)[J]. 电工技术学报, 2015(S1)： 320-328.

[11] 武星, 宫芳涛, 赵阳杰. 微电网能量管理解决方案[J]. 电气技术, 2014, 15(S1)： 92-93.

[12] 奚玲玲. 分布式能源微网控制保护与能量管理解决方案[J]. 电气技术, 2014, 15(S1)： 79-81.

[13] 侯李祥, 卓放, 师洪涛, 等. 基于系统稳定性分析的微电网阻抗测量技术[J]. 电工技术学报, 2015,30(22)： 153-162.

[14] 王成山, 武震, 李鹏. 微电网关键技术研究[J]. 电工文摘, 2014(2)： 59-68.

[15] 李晔, 贺启飞, 张保会. 感应电动机稳定性判别与切负荷控制[J]. 智能电网, 2016, 4(4)： 374-378.

[16] 刘楠, 张彦涛, 秦晓辉, 等. 感应电动机负荷对短路电流影响机理研究[J]. 电网技术, 2012(8)： 187-192.