Controlling Thermodynamic Properties of Ferromagnetic Group-IV Graphene-Like Nanosheets by Dilute Charged Impurity

Mohsen Yarmohammadiand Kavoos Mirabbaszadeh

Department of Energy Engineering and Physics,Amirkabir University of Technology,Tehran,Iran

1 Introduction

The properties of graphene,the one-atom-thick sheet of carbon atoms with thesp2hybridization,were first discussed in the literature more than sixty years ago.[1]Since then,graphene has been intensively investigated with focus on its physical and chemical properties.[2]Because of its unique symmetry,electron and hole bands of graphene show linear band crossing at the Fermi level,[3]resulting in a massless Dirac fermion like behavior of charge carriers.It has found several two-dimensional(2D)materials like group-IV graphene-like structures,hexagonal boron-nitride(h-BN)and MoS2,which present null gaps in both flat or buckled con figurations.Although these materials have a honeycomb lattice,but their properties are different.[4−8]The band gap is a measurement of the threshold voltage and on-off ratio of the field effect transistors.[9−10]In recent years,elemental sheets of silicon and germanium(silicene and germanene respectively)have been emerging as strong contenders in the realm of 2D materials.[11−12]There have been several theoretical studies assessing their fundamental properties while experimental analyses are just in their infancy,as practical synthesis methods are being explored to establish well defined fabrication techniques and parameters.Studies predict that such elemental sheets may also possess Dirac fermions similar to graphene and much simpler techniques may become available for their band gap engineering.Although semi-metallic,the main hurdle experienced in realizing silicene and germanene is that unlike graphene,they do not form a van der Waals layered structures in their bulk phase.Hence,they do not exist as freestanding sheets but synthesized as adlayer structures on ordered substrates.[13]Despite this fact,the exceptional findings through theoretical and preliminary experimental analyses,along with its compatibility to the current silicon based electronics,continues to inspire the exploration of 2D silicene and other group-IV elemental materials(germanene,stanene).However,a lot remains to be explored before these materials can be established as viable alternatives for the next generation of electronic applications.[14−15]

Successful realization of single crystal silicon monolayer structures[16−17]through chemical exfoliation shows that 2D silicon monolayers with their low resistivity and extremely thin structures can be quite promising for nanoelectronics. Unlike graphene,silicene has a hexagonal atomic arrangement with a buckled con figuration because of its large ionic radius of silicon atoms,[18−21]as presented in Fig.1.From this point,its sublattices(AandB)sit in two parallel planes with a vertical distance of 0.46 ˚A.[22−23]The low-energy dynamics of fermions in pristine graphene describes by Dirac Hamiltonian but in silicene,germanene and stanene due to the strong spinorbit coupling(SOC),carriers are massive with an energy gap.[24−25]This gap can be modulated via an applied perpendicular EF to its layer,which leads to the many attractive properties.[26−33]Unlike electronic properties,thermal properties of group-IV are still not well studied.Many works show that the thermal conductivity of silicene is predicted around(20–65)W/mK.[34−38]Electronic heat capacity(EHC)of a semiconductor system is defined as the ratio of the heat used by the carriers(here,Diracfermions)to the rise in temperature of the system.[39]On the other hand,magnetic susceptibility(MS)is the degree of magnetization of a material in response to an external applied magnetic field.Furthermore,our system is considered as a ferromagnetic with an exchange field.Electrons in a system scatter from dilute charged impurities with a scattering rate.This induces a characteristic energy scale at Dirac points.For this reason,impurities have a strong effect on physical properties of materials such as electronic and thermal properties for their applications in electronic devices.Motivated by the recent experimental developments and theoretical investigations on 2D monolayer honeycomb structures,in this paper we carry out a systematic study of three similar structures of group-IV elements based on the Green’s function method.

In this work,we have investigated the temperature dependence of EHC and MS in ferromagnetic silicene,germanene and stanene in the presence of dilute charged impurity at Dirac points.Also,at a given impurity concentration(IC)and impurity scattering strength(ISS),EHC and MS have been studied with EF.Green’s function approach is carried out with the Kane-Mele Hamiltonian to study the dynamics of carriers in the system.In this work,impurities are randomly doped on sheets.The organization of this paper is as follows:In Sec.2,the methods together with parameters used in our calculations are outlined.The thermodynamic properties of these structures are investigated in Sec.3.In Sec.4,we present our results regarding the calculations.In Sec.5,our conclusions are presented.

2 Methods

Here is considered a monolayer system on thexy-plane,exposed to the perpendicular EFEz,as illustrated in Fig.1.The system is described by following model in order to study the dynamics of carriers[25,40]

in which the first term denotes the nearest-neighbor hopping with energy oft0and the sum runs over all neighboring pairscreates(annihilates)an electron with spinσ=↑,↓ at sitei.The first two terms illustrate the Kane–Mele Hamiltonian describing the SOC with ΔSO,being→σ=(σx,σy,σz)the Pauli matrices.Also is defined

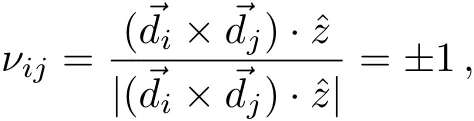
with→diand→djbeing the two typical vectors,which connect the next nearest neighbors,and sum over all such pairs indicated by 〈i,j〉.[41−42]The third term is the staggered sublattice potential term as mentioned before in Sec.1 withςi=+1(−1)forA(B)sites.The final term is related to the induced exchange magnetic field by the magnetic insulator substrate.The low-energy limit of the above Hamiltonian in a ferromagnetic system in presence of a perpendicular uniform EF is described as:[25,43]

whereinvFis the Fermi velocity of carriers for the inplane momentum k=(kx,ky)of the first Brillouin zone.ais the equilibrium lattice constant of structures andτi(i=x,y,z)are the Pauli matrices in the sublattice space.The first term in Eq.(1)is the pristine graphene Hamiltonian(Dirac Hamiltonian)at Dirac cone approximation forK(K′)points indexed byη=+1(−1).This term refers to the intra-layer hopping fromAatoms toBatoms and vice versa.The second term is the Kane–Mele Hamiltonian for the intrinsic SOC.[44]If systems rest onto the surface of a magnetic insulator substrate,an exchange magnetization can be induced asM= ΔSO/2.[45−46]σ=+1(−1)are used for spin-up and spin-down subbands.The Green’s function matrix of the unperturbed system can be readily obtained by following equation

Having substituted Eq.(2)into Eq.(3),the explicit form of the Green’s function matrix is found but has not been written here because it is quite lengthy.The lattice constantsa,SOC and Fermi velocity at the Dirac pointKare given as((3.86,4.02 and 4.70)˚A),((5.42,5.24 and 4.70)×105m/s)and((1.55,23.9 and 73.5)meV)for(silicene,germanene and stanene),respectively.[25]According to the Born approximation in the scattering theory[47]and usingTmatrix,[47]the electronic self-energy matrix of disordered system in the presence of finite but small density of impurity atoms,ni=Ni/N,could be obtained as

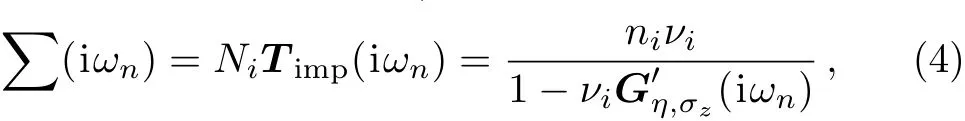
whereNis the number of unit cell atoms andνidenotes the electronic on-site energy,which shows the strength of scattering potential.The local propagator of unperturbed system is given by

In order to include some contributions from multiple site scattering,we replace the local bare Green’s functionby local full one,in the expression of the self-energy matrix in Eq.(4),leading to full self-consistent Born approximation.Under neglecting interstice correlations,the self-consistent problem requires the solution of equation

The electronic self-energy should be found from a selfconsistent solution of Eq.(6).The pertubative expansion for the Green’s function of disordered system is obtained via the Dyson equation[47]as

In the next section,EHC and MS are calculated.

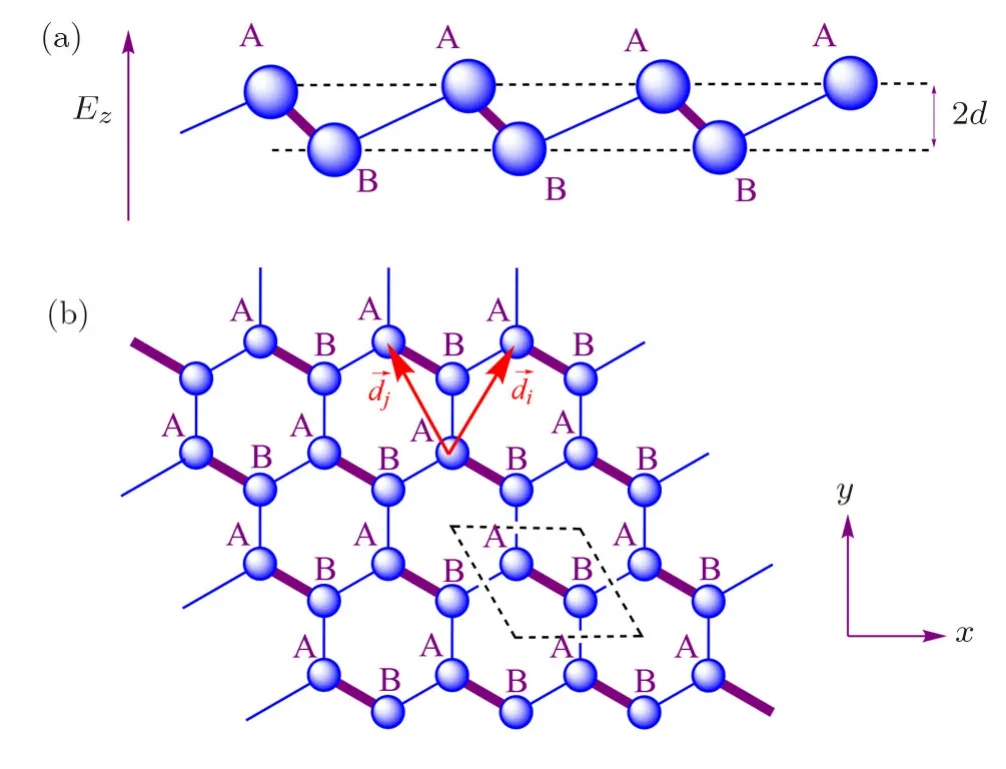
Fig.1 The(a)side view and(b)top view schematic illustration of group-IV graphene-like nanosheets.The A and B sites separated by a distance 2d within the electric field(EF)Ez.The black dashed lines illustrate the Bravais unit cell including two atoms.→diand→djare two typical vectors connecting the next nearest neighbors.

3 Electronic Heat Capacity and Magnetic Susceptibility

Density of states(DOS)can be calculated by trace of the imaginary part of the Green’s function matrix,D(ε)= −ℑ TrG(ε)/π.[48]Taking trace over the quantum numbers,which label the Hamiltonian,engaging Eqs.(1)and(3)along with setting iωn→ε+i0+as an analytical continuation(being 0+a very small real number),the total DOS would be eventuated

whereµdescribes a sub-site andNcis the number of unit cells.The EHC could be introduced by following expression[39]

in whichD(ε)calculated by Eq.(8)andf(ε) =1/[eε/kBT+1](kBis the Boltzmann constant)represents the Fermi–Dirac distribution function.By using Eqs.(8)and(9),the EHC would be obtained as

and MS could be introduced by following expression[39]

in whichf(E)=1/[eε/kBT+1](beingkBthe Boltzmann constant)stands for the Fermi–Dirac distribution function.Calling Eqs.(8)and(11),the MS would be obtained by

4 Numerical Results

In this section,taking into account Eqs.(2),(7),(10),and(12),we obtain the entire low-energy EHC and MS curves around the DiracKpoint and spin-up because of the much number of results besides theK′point and spindown.Because of the unique structure of aforementioned nanosheets and also a symmetry behavior between DiracK(K′)point with spin-up(down)andK′(K)point with spin-down(up),as verified in Refs.[26–27,30,32],we have focused on theKpoint and spin-up cases for reduction of the same results and curves.Also,we have completed our numerical calculations based on the reported parameters in Ref.[25].

It is well-known that EHC of semiconductors at low temperatures is given byC(T)∝ e−Δ/kBT.[39,49]We see that all curves for EHC exhibit the same behavior with respect to the temperature.Remarkable in every curve is an anomalous peak,so-called the Schottky anomaly,which appears over a small range of temperatures when thermal energy reaches to the energy gap between the subbands.[50−51]The Schottky anomaly as an interesting effect can be explained in terms of the changing in the entropy of the system.As we know,at zero temperature only the lowest energy level is occupied and the entropy is equal to zero.In this regard,there is a very little probability of transition to a higher energy level.As soon as the temperature increases,the entropy increases too monotonausly and therefore the probability of the transition goes up.As soon as the temperature closes to the difference between the energy levels in the system,a broad peak appears,which is corresponding to a large change in the entropy for a small change in temperature.At high temperatures,all of levels are occupied,so there is again a little change in the entropy for small changes in temperature and thus a lower heat capacity.[52−53]Here Δ is the combined EF and impurity scattering potentials.Interaction between conducting electrons and dilute charged impurities affects the scattering rate of electrons.

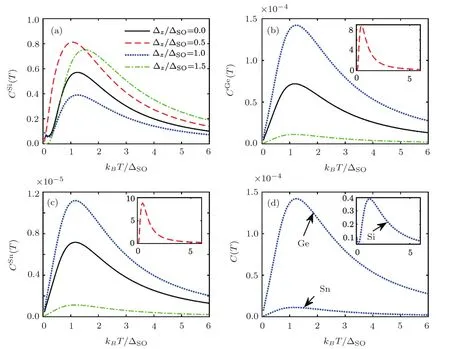
Fig.2 Electronic heat capacity in terms of temperature at different electric field strengths for(a)silicene,(b)germanene,(c)stanene and(d)all structures at Δz= ΔSO.

Fig.3 As Fig.2 but for magnetic susceptibility.

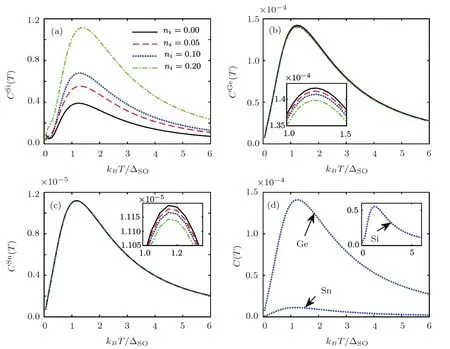
Fig.4 Temperature-dependent electronic heat capacity for various impurity concentrations for(a)silicene,(b)germanene,(c)stanene and(d)all structures at Δz= ΔSO,νi=0.4ΔSOand ni=0.1.

Fig.5 Similar to Fig.4 but for magnetic susceptibility.

Fig.6 Temperature behavior of electronic heat capacity for various impurity scattering strengths for(a)silicene,(b)germanene,(c)stanene and(d)all structures at Δz=(3/2)ΔSO,νi=0.4ΔSOand ni=0.1.

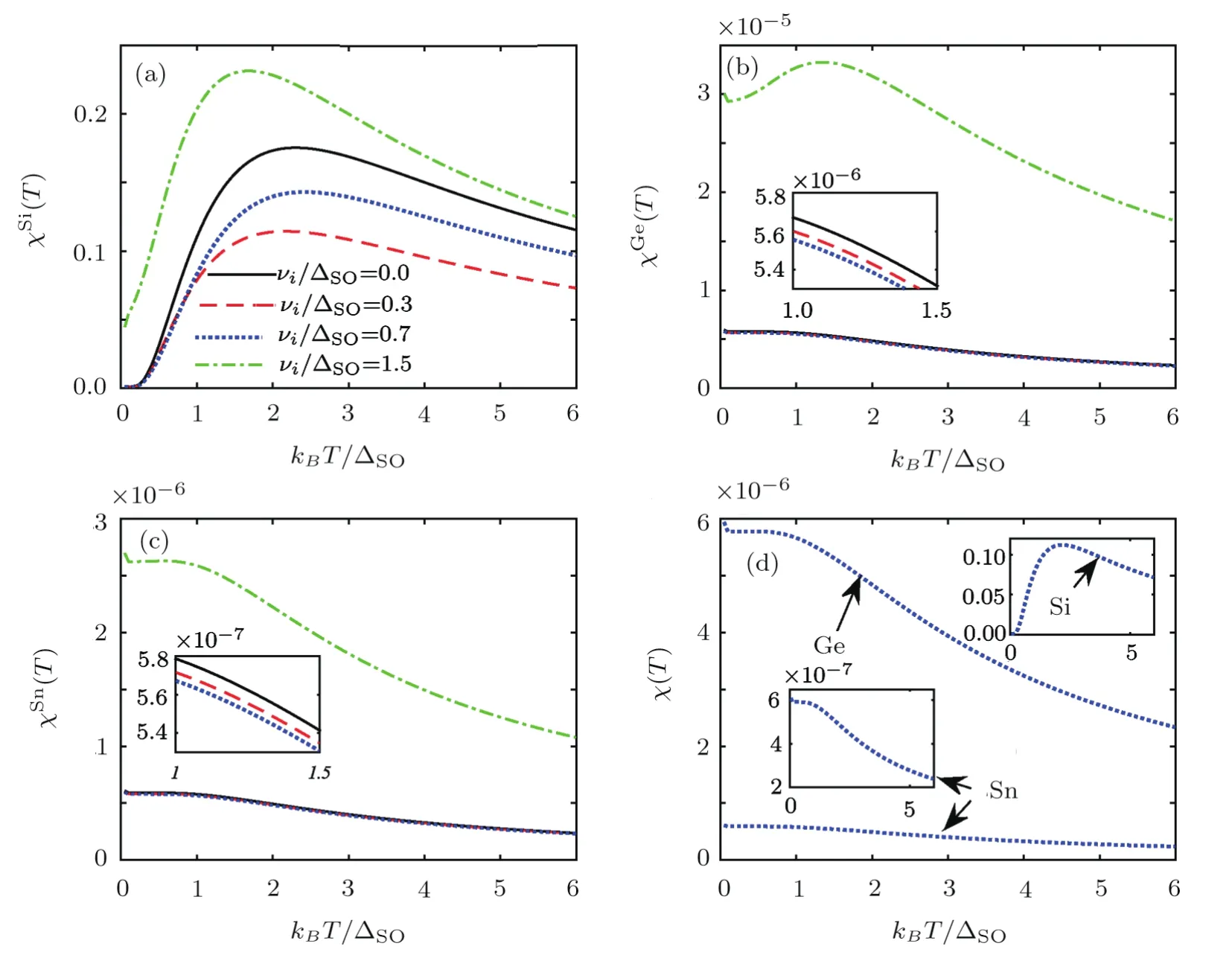
Fig.7 Like Fig.6 but for magnetic susceptibility.

The evaluation of EHC with EF has been presented in Fig.2.For silicene,spin-up band gap decreases at Δz≤ ΔSOwhile increases at Δz＞ΔSO,which is in agreement with derived findings in Ref.[32].It means that the Schottky anomaly appears atkBT＜ΔSO(kBT＞ΔSO)for Δz＜ΔSO(Δz＞ΔSO).For germanene and stanene structures,the spin-up band gaps remain constant because of their large SOC,which does not allow the quantum states to change with EF.In fact,change of Δzin comparison with these large SOCs is negligible.For these nanosheets,there is a critical EF,Δz=(1/2)ΔSO,where EHC is maximum.At low EF strengths,scattering rate is normal and systems see EF as a perturbation that affects their electron transports,but at Δz= ΔSO,systems back to their initial states because of the uniform EF with a smaller transport.For Δz＞ΔSO,systems encounter with a unusual scattering rate and EHC increases.These are invalid for germanene and stanene because of their large SOC.For Δz＞ΔSO,we have minimum EHC for germanene and stanene structures.In Fig.2(d),silicene(stanene)has the maximum(minimum)EHC at Δz=ΔSO.

Figure 3 show the temperature-dependent magnetic susceptibility like Fig.2.Each curve bears a crossover,which originates from degenerated energy levels in the electronic minibands and parts the susceptibility into two temperature regions with a sharp positive slope before the apex and a relatively less negative slope after that.[52]According to the concept of magnetic susceptibility,which is a famous topic in every magnetic books and literatures,we have three magnetic orders based on the MS curves for spins including antiferromagnetic,ferromagnetic and paramagnetic.Susceptibility appears as response of the system to the interaction between magnetic field and spin of carriers,which changes the net magnetization of the system.To investigate the temperature behavior of susceptibility,the competition between thermal energy and mentioned interaction plays a key role in the system,leading to the change of magnetization.It is shown that at low temperatures,spin ordering of antiferromagntic systems changes interestingly with magnetic field and MS increases with temperature(albeit in small ranges).When thermal energy reaches to the band gap size of the system,MSmaxoccurs and after that MS decreases,i.e.,system does not answer to magnetic field at high temperatures.Generally,at low temperatures,magnetic field is dominant and MS increases while at high temperatures,temperature is dominant and MS decreases but with a critical temperature,known as Neel temperature.In fact,magnetic field at low temperatures flips the spins and the number of spins with the same directions increases,which leads to the increase of MS but at high temperatures,magnetic field cannot flip the spins and MS decreases because of the high scattering rate of carriers at high temperatures,as shown in the following figure.In ferromagnetic state,all spins have the same directions and at low temperatures,MS decreases with a severe slope up to the Curie temperature.Finally,paramagnetic materials have the random spin directions and MS decreases slightly with temperature because of the weak coupling between spins and external magnetic field.At first,spin-up have the ferromagnetic con figuration while for Δz＜ΔSOand Δz＞ΔSO,silicene show antiferromagnetic phase and transitions to paramagnetic at Δz= ΔSO.These changes are not valid for germanene and stanene structures and only at Δz＜ΔSO,systems show the antiferromagnetic phase.

Presented in Fig.4 are temperature-dependent EHC for various ICs at Δz= ΔSOandνi/ΔSO=0.4.One can see that EHC increases withniand the band gap size does not change for silicene.Interestingly,EHC decreases withnifor germanene and stanene,which it can be understood by their large intrinsic SOC.Also,it is necessary to say that these changes are at 1＜kBT/ΔSO＜2 and 1＜kBT/ΔSO＜3/2 for germanene and stanene,respectively.Figure 4(d)presents silicene(stanene)has the EHCmax(EHCmin).Figure 5 shows that impurity transited the magnetic order of the spins-up from paramagnetic to ferromagnetic phase by flipping.Germanene and stanene do not have phase transition withni.Silicene(stanene)responses to the external magnetic field as maximum(minimum)behavior as shown in Fig.5(d).

Finally,we have investigated the temperature behavior of EHC and MS of these systems for various ICCs in Figs.6 and 7.Generally,EHC decreases withνi/ΔSOin silicene.Also,the band gap decreases withνi/ΔSObecause the crossover moves towards the lower temperatures.In germanene and stanene,EHC decreases slightly withνi/ΔSOup toνi＜ΔSOwhile increases forνi＞ΔSO.For MS results,according to the previous descriptions on magnetic order,silicene’s phase is antiferromagnetic while germanene and stanene are at ferromagnetic phase and all structures have MSmaxatνi＞ΔSO.

5 Summary

In summary,based on symmetry aspects and the massive Dirac theory combined with the Green’s function method,we derived the temperature behavior electronic heat capacity and magnetic susceptibility of silicene,germanene and stanene with electric field,impurity concentration and impurity scattering strength.Spin-up band gap changes with the mentioned above quantities because of the change of the scattering rate of carriers.We have found that the impurity-dependent magnetic susceptibility curves lead to a phase transition from ferromagnetic to paramagnetic and antiferromagnetic phases.

[1]A.H.Castro Neto,F.Guinea,N.M.R.Peres,K.S.Novoselov,and A.K.Geim,Rev.Mod.Phys.81(2009)109.

[2]A.K.Geim,Science 324(2009)1530.

[3]P.R.Wallace,Phys.Rev.71(1947)622.

[4]K.F.Mak,C.Lee,J.Hone,J.Shan,and T.F.Heinz,Phys.Rev.Lett.105(2010)136805.

[5]A.H.Castro Neto,F.Guinea,N.M.R.Peres,K.S.Novoselov,and A.K.Geim,Rev.Mod.Phys.81(2009)109.

[6]N.M.R.Peres,Rev.Mod.Phys.82(2010)2673.

[7]D.Pacile,J.C.Meyer,C.O.Girit,and A.Zettl,Appl.Phys.Lett.92(2008)133107.

[8]K.S.Novoselov,D.Jiang,F.Schedin,T.J.Booth,V.V.Khotkevich,S.V.Morozov,and A.K.Geim,Proc.Natl.Acad.Sci.USA 102(2005)10451.

[9]Y.Lin,K.A.Jenkins,A.Valdes-Garcia,J.P.Small,D.B.Farmer,and P.Avouris,Nano Lett.9(2009)422.

[10]J.Kedzierski,P.Hsu,P.Healey,P.W.Wyatt,C.L.Keast,M.Sprinkle,C.Berger,and W.A.de Heer,IEEE Trans.Electron Devices.55(2008)2078.

[11]Q.Tang and Z.Zhou,Prog.Mater.Sci.58(2013)1244.

[12]L.C.L.Yan Voon and G.G.Guzmn-Verri,MRS Bull.39(2014)366.

[13]P.Vogt,P.De Padova,C.Quaresima,J.Avila,E.Frantzeskakis,M.C.Asensio,A.Resta,B.Ealet,and G.Le Lay,Phys.Rev.Lett.108(2012)155501.

[14]L.Li,Y.Yu,G.J.Ye,Q.Ge,X.Ou,H.Wu,D.Feng,X.H.Chen,and Y.Zhang,Nat.Nanotechnol.9(2014)372.

[15]H.Liu,A.T.Neal,Z.Zhu,Z.Luo,X.Xu,D.Tomnek,and P.D.Ye,ACS Nano 8(2014)4033.

[16]H.Nakano,T.Mitsuoka,M.Harada,K.Horibuchi,H.Nozaki,N.Takahashi,T.Nonaka,Y.Seno,and H.Nakamura,Angew Chem.118(2006)6451.

[17]R.Krishnan,Q.Xie,J.Kulik,X.D.Wang,S.Lu,M.Molinari,Y.Gao,T.D.Krauss,and P.M.Fauchet,J.Appl.Phys.96(2004)1.

[18]B.Lalmi,H.Oughaddou,H.Enriquez,A.Kara,S.Vizzini,B.Ealet,and B.Aufray,Appl.Phys.Lett.97(2010)223109.

[19]P.E.Padova,C.Quaresima,C.Ottaviani,et al.,Appl.Phys.Lett.96(2010)261905.

[20]B.Aufray,A.Vizzini,H.Oughaddou,C.Lndri,B.Ealet,and G.L.Lay,Appl.Phys.Lett.96(2010)183102.

[21]P.Vogt,P.De Padova,C.Quaresima,et al.,

[22]Z.Ni,Q.Liu,K.Tang,et al.,Nano Lett.12(2012)113.

[23]N.D.Drummond,V.Z’olyomi,and V.I.Fal’ko,Phys.Rev.B 85(2012)075423.

[24]C.C.Liu,W.Feng,and Y.Yao,Phys.Rev.Lett.107(2011)076802.

[25]C.C.Liu,H.Jiang,and Y.Yao,Phys.Rev.B 84(2011)195430.

[26]M.Ezawa,New J.Phys.14(2012)033003.

[27]M.Ezawa,Phys.Rev.Lett.109(2012)055502.

[28]X.T.An,Y.Y.Zhang,J.J.Liu,and S.S.Li,New J.Phys.14(2012)083039.

[29]M.Tahir and U.Schwingenschlogl,Sci.Rep.3(2013)1075.

[30]M.Ezawa,Phys.Rev.Lett.110(2013)026603.

[31]W.F.Tsai,C.Y.Huang,T.R.Chang,H.Lin,H.T.Jeng,and A.Bansil,Nat.Commun.4(2013)1500.

[32]C.J.Tabert and E.J.Nicol,Phys.Rev.Lett.110(2013)197402.

[33]H.Pan,Z.Li,C.C.Liu,G.Zhu,Z.Qiao,and Y.Yao,Phys.Rev.Lett.112(2014)106802.

[34]E.Scalise,M.Houssa,G.Pourtois,B.Broek,V.Afanasev,and A.Stesmans,Nano Res.6(2013)19.

[35]H.P.Li and R.Q.Zhang,Eur.Phys.Lett.99(2012)36001.

[36]M.Hu,X.Zhang,and D.Poulikakos,Phys.Rev.B 87(2013)195417.

[37]Q.X.Pei,Y.W.Zhang,Z.D.Sha,and V.B.Shenoy,J.Appl.Phys.114(2013)033526.

[38]T.Y.Ng,J.Yeo,and Z.Liu,Int.J.Mech.Mater.Des.9(2013)105.

[39]C.Kittle,Introduction to Solid State Physicseighth ed.Wiley,New York(2004).

[40]B.Aufray,A.Vizzini,H.Oughaddou,C.Lndri,B.Ealet,and G.L.Lay,Appl.Phys.Lett.96(2010)183102.

[41]C.L.Kane and E.J.Mele,Phys.Rev.Lett.95(2005)146802.

[42]C.L.Kane and E.J.Mele,Phys.Rev.Lett.95(2005)226801.

[43]T.Yokoyama,Phys.Rev.B 87(2013)241409(R).

[44]L.Chen,B.J.Feng,and K.H.Wu,Appl.Phys.Lett.102(2013)081602.

[45]H.Haugen,D.Huertas-Hernando,and A.Brataas,Phys.Rev.B 77(2008)115406.

[46]Z.Qiao,S.A.Yang,W.Feng,et al.,Phys.Rev.B 82(2010)161414.

[47]W.Nolthing and A.Ramakanth,Quantum Theory of Magnetism,Springer,New York(2009).

[48]E.N.Economou,Green’s Functions in Quantum Physics,3rd ed.Springer-Verlag,Berlin,Heidelberg(2006).

[49]R.K.Pathria,Statistical Mechanics,Oxford Press,London(1997).

[50]B.Velicky,Phys.Rev.184(1969)614.

[51]M.Yarmohammadi,Solid State Commun.250(2017)84.

[52]A.Tari,The Specific Heat of Matter at Low Temperatures,Imperial College Press,London(2003)p.250.

[53]X.Xu,J.Chen,and B.Li,J.Phys.Condens.Matter.28(2016)483001.