PA 6/PET扁平复合纤维界面分布的数值模拟
叶 贺,潘 俊,张荣根,冯 培*,杨崇倡,
(1.东华大学 机械学院,上海 201620; 2.纺织装备教育部工程研究中心,上海 201620)
复合异形纤维纺丝成形过程中,熔体间界面位置分布稳定性是影响复合异形纤维成形质量的关键因素[1]。当两种聚合物熔体在异形微孔流道内流动时,不同的微孔结构参数和纺丝工艺参数会使两种聚合物熔体流动速度和压力产生差异,导致纺丝过程产生不稳定层流,界面位置分布不稳定,导致纺丝时丝条产生扭曲、粘板等现象。
复合纤维的纺丝成形过程中,熔体界面分布的研究大多聚焦于研究聚合物材料、流变特性以及温度对界面分布的影响[2-4],且传统复合纤维的纺丝成形研究[5-7]通常忽略熔体的壁面滑移效应,而在实际纺丝中,喷丝板扁平微孔的长宽比(W/H)、微孔深度(L)以及熔体流量比对纤维成形也具有重要的影响,且壁面滑移的影响不可忽略。因此,作者以聚对苯二甲酸乙二醇酯(PET)和聚己内酰胺(PA 6)为例,分析两种聚合物熔体在复合喷丝板扁平孔道内流动,在动力学数学模型的基础上,考虑壁面滑移这一弹性行为,进行数值模拟,研究扁平微孔的W/H、L以及熔体流量比对复合熔体PA 6和PET界面位置分布的影响。
1 数值方程及模拟参数的设定1.1 纺丝动力学数学模型
理论状态下,复合异形纤维成形过程遵循三大守恒的基本定律,假定熔体不可压缩的前提下,忽略惯性项、丝条重力的影响。其能量方程、动量方程、连续性方程分别如式(1),(2),(3)所示。

(1)
η▽2V-▽P=δ/R
(2)

(3)
式中:ρ为密度;t为时间;V为速度矢量;Cv是熔体的体积热容;T为温度;K为热传导率;τ为应力张量;P为压力;η是黏度;δ为表面张力;R为高斯曲率。
1.2 滑移因子的确定
参照Mooney[8]的方法研究壁面滑移行为:在熔融纺丝过程中,考虑壁面滑移这一弹性行为,假定聚合物熔体不可压缩且为稳态层流,则在扁平微孔中,其滑移速度方程、扁平微孔流量方程以及形状因子方程分别如式(4),(5),(6)所示。
Vs=θξm
(4)
(5)
(6)
式中:Vs为滑移速度;θ为滑移系数;m为幂律指数;ξ为壁面处的剪切应力;W为扁平微孔长度;H为扁平微孔宽度;Q为单孔体积流量;Fq为形状因子;i为1,3,5....;h为函数变换系数。
一般而言,扁平微孔中,W/H大于10,其Fq小于1,故当其在同样体积流量下,与常规矩形微孔形状相比,扁平孔道中聚合物熔体流动时需要的压力降更高。参照汪春[9]所做壁面滑移研究,PET和PA 6熔体的θ分别取为1.5,1.2。
1.3 几何模型
建立几何模型,如图1所示。BS1为PET入口;BS2为PA 6入口;BS3为喷丝孔壁面;BS4为PET与PA 6交界面; BS5为自由面(纤维表面)。
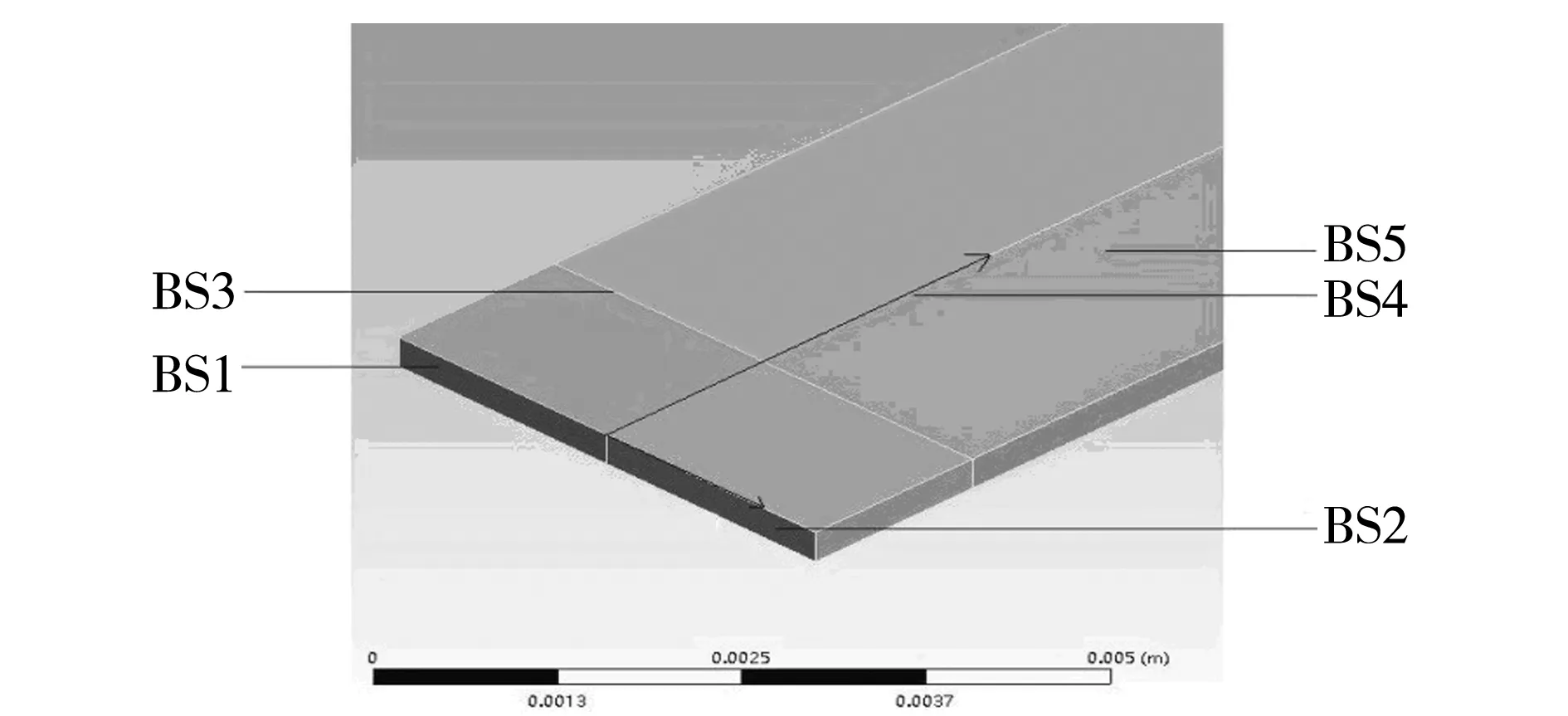
图1 扁平微孔几何模型Fig.1 Geometric model of flat microhole
1.4 模拟参数的设定
模拟参数包括材料物性参数和模拟纺丝工艺参数,见表1和表2。其中,n为非牛顿指数,λ为松弛时间,η0为零切黏度,Cp为热容量,T1为纺丝入口温度,T2为纺丝冷却温度。
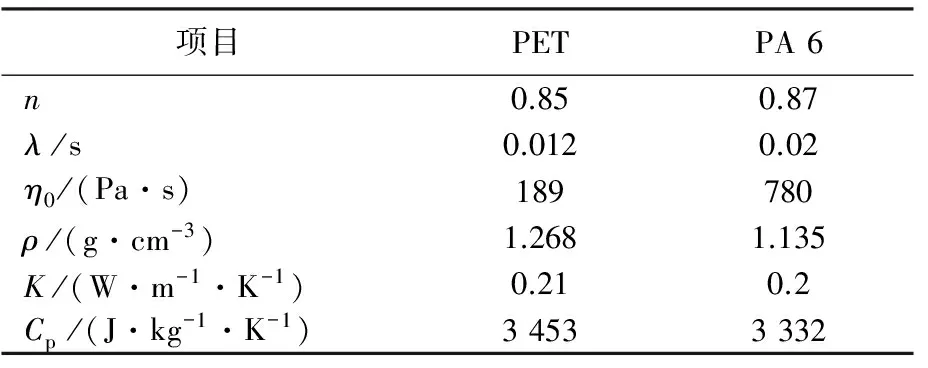
表1 材料物性参数Tab.1 Physical index of feedstocks

表2 模拟纺丝工艺参数Tab.2 Simulated spinning process parameters
1.5 边界条件
数值模拟时,设定以下边界条件:两种流体的流动没有穿透界面;界面之间没有相对滑移;界面上两种聚合物熔体切向速度相同;两侧切向应力张量相等;孔道边界添加滑移系数;流动出口设定作用零法向力和零切向力。
1.6 数值模拟计算
(7)
式中:η∞为无穷零切黏度。
有限元数值计算的迭代算法为Pi-card迭代算法,速度采用Mini-element线性插值,微孔部分设置3D网格重置。
2 结果与讨论
2.1 微孔W/H对界面位置分布的影响
为研究喷丝板微孔W/H对界面位置的影响,在Q为3.2×10-7m3/s、PET:PA 6流量比为1:1不变的情况下,喷丝板微孔L为1.5 mm,喷丝板微孔W/H根据工厂经验分别设置为10,11,12,13,研究熔体流动过程中的界面位置分布规律,计算结果如图2所示。本文中的界面位置偏移量是指PA 6和PET的界面位置偏移量;偏移量为正,代表PET一侧偏向PA 6一侧,偏移量为负,代表PA 6一侧偏向PET一侧;界面相对偏移量可理解为整体变化趋势。

图2 不同W/H时喷丝板孔道内界面位置分布Fig.2 Interface position distribution in spinneret hole with different W/H ratioW/H:1—10;2—11;3—12;4—13
由图2可知,界面偏移量为正,表示PA 6/PET扁平复合纤维界面由PET一侧偏向PA 6一侧。在一定范围内,W/H的不同仅对熔体界面位置产生一定的影响,而对相对偏移量没有产生影响,即随着W/H增大,界面位置偏移量逐渐增大。
由图3可以发现,喷丝板W/H的变化对熔体两侧压力分布影响不大。故喷丝板微孔W/H的变化主要影响到熔体界面位置偏移量的分布。

图3 不同W/H时熔体的等压线分布Fig.3 Isopiestic distribution of melt at different W/H ratio
2.2 微孔L对界面位置分布的影响
为研究微孔L对界面位置的影响,在Q为3.2×10-7m3/s、PET:PA 6流量比为1:1不变的情况下,喷丝板微孔W/H设定为10,分别将微孔L设置为1.2,1.5,1.8,2.0 mm,研究不同L对界面位置分布的影响,结果如图4所示。
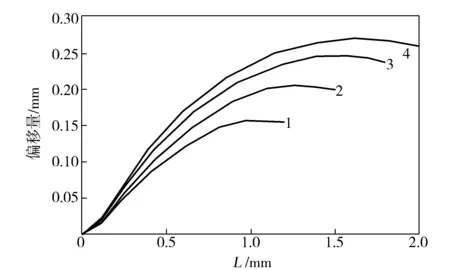
图4 不同L时喷丝板孔道内界面位置分布Fig.4 Interface position distribution in spinneret holes with different LL:1—1.2 mm;2—1.5 mm;3—1.8 mm;4—2.0 mm
由图4可知,界面偏移量为正,表示PA 6/PET扁平复合纤维界面由PET一侧向PA 6一侧偏移。不同的L影响熔体在孔道内流动时的界面分布位置,随着喷丝板L的增大,熔体界面位置偏移量逐步增大,界面相对偏移量也逐步增大。
通过图5对比不同L时熔体的等压线分布可知,熔体两侧压力分布相对均匀,同一截面处压力差别不大。

图5 不同L时熔体的等压线分布Fig.5 Isopiestic distribution of melt at different L
2.3 流量比对界面位置分布的影响
为研究流量比对界面位置的影响,在Q为3.2×10-7m3/s,W/H为10,L为1.5 mm,纺丝温度设定在290 ℃时,设定不同的PET/PA 6流量比。PA 6:PET流量比为1:1,1:2,1:3,2:1,3:1进行数值模拟,计算结果如图6所示。
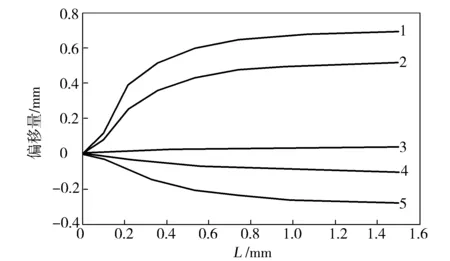
图6 不同PA 6/PET流量比时喷丝板孔道内界面位置分布Fig.6 Interface position distribution in spinneret hole at different PA 6/PET flow ratioPA6:PET流量比:1—1:3;2—1:2;3—1:1;4—2:1;5—3:1
由图6可知,偏移量为正时,表示熔体界面偏向于PA 6一侧,当其为负时,表示熔体界面偏向于PET一侧。复合纺丝时,不同的PA 6/PET流量比会对熔体界面的分布产生较大的影响,会导致喷丝板孔道内熔体界面发生偏移,流量比对喷丝板孔道内的熔体界面的相对偏移量影响较小,但是其对熔体界面位置分布影响巨大。
由图7可以看出,当PET:PA 6流量比为1:1时,界面两侧的剪切流动基本呈对称分布,此时的界面偏移主要是由于PET/PA 6的流动特性差异造成的,即PET流动性差于PA 6流动性,导致界面偏向于PA 6一侧;当PET:PA 6流量比为2:1时,界面位置偏向于PET一侧,原因是PET流量增大时,根据非牛顿流体的剪切变稀特征,界面两侧的剪切速率差值增大,熔体黏度差异增加,引起界面偏移增大,此时界面偏移主要由PET流量的加大导致界面两侧差异的增大造成,此时流量比对界面分布的影响大于材料特性对界面分布的影响。随着PA 6/PET流量比的增大,熔体界面位置偏移量由PA 6一侧逐步减小至PET一侧反向逐步增大;通过图6对比其等压线分布可知:同一截面处的压力差异随着PA 6/PET流量比的增大而逐步减小至反向增大。

图7 不同PA 6/PET流量比时熔体的等压线分布Fig.7 Isopiestic distribution of melt at different PA 6/PET flow ratios
3 结论
a. 在一定范围内,随着W/H值的增大,界面位置偏移量逐渐增大,相对偏移量没有变化;喷丝板W/H的变化对同一截面处熔体两侧压力分布差异影响不大。
b. 不同的喷丝板L影响扁平熔体在孔道内流动时的界面分布位置,随着喷丝板L的增大,熔体界面位置偏移量逐步增大,界面相对偏移量也逐步增大;但熔体两侧压力分布相对均匀,同一截面处压力差异不大。
c. 当总流量不变的情况下,不同的PA 6/PET流量比对界面偏移量的影响很大,随着PA 6/PET流量比的增大,熔体界面位置偏移量由PA 6一侧逐步减小至PET一侧反向逐步增大;同一截面处的压力差异随着PA 6/PET流量比的增大而逐步减小至反向增大。合理的流量比能够减小界面偏移量,改善纺丝时复合扁平纤维的成形效果。
d. 扁平纤维界面分布的数值模拟对与PA 6:PET物性指标类似的其他高聚物的复合纺丝具有指导意义。
参 考 文 献
[1] 纪占国.分层界面滑移对聚合物共挤成型过程影响的数值模拟研究[D].南昌:南昌大学,2008.
Ji Zhanguo.The numerical simulation on influence of interfacial slipping on polymer co-extrusion molding process[D].Nanchang:Nanchang University,2008.
[2] Han C D, Shetty R.Studies on multilayer film coextrusion. I. The rheology of flat film coextrusion[J]. Polym Eng Sci,1976,16(10):697-705.
[3] Puissant S, Vergnes B, Demay Y, et al. A general non-isothermal model for one-dimensional multilayer coextrusion flows[J]. Polym Eng Sci,1992, 32(3):213-220.
[4] Matsunaga K, Kajiwara T, Funatsu K. Numerical simulation of multi-layer flow for polymer melts-A study of the effect of viscoelasticity on interface shape of polymers within dies[J]. Polym Eng Sci,1998,38(7):1099-1111.
[5] 杨崇倡,谭志强,魏蕊,等.扁平纤维纺丝成形研究Ⅰ.扁平纤维纺丝成形的数字模型及模拟分析[J].合成纤维工业,2009,32(3):56-59.
Yang Chongchang,Tan Zhiyin,Wei Rui,et al. Study on flat fiber formation Ⅰ.Mathematical model and simulation analysis of flat fiber formation[J].Chin Syn Fiber Ind,2009,32(3):56-59.
[6] 吕洪,刘正恒,马驿,等.PBT/PET 并列型复合纺丝的研究[J].合成技术及应用,1995,10(1):8-14.
Lv Hong, Liu Zhengheng,Ma Yi, et al.Study on PBT/PET side-by-side conjugate spinning[J]. Syn Tech Appl,1995,10(1):8-14.
[7] 张敏, 孙胜, 贾玉玺. 双层聚合物共挤出过程的数值模拟[J].高分子材料科学与工程,2005,21(6):15-19.
Zhang Min, Sun Sheng, Jia Yuxi.Numerical simulation of double-layer polymer coextrusion process[J]. Polym Mater Sci Eng,2005, 21(6):15-19.
[8] Mooney M. Explicit formulas for slip and fluidity[J]. J Rheol,1931(2):210-222.
[9] 汪春. 纺丝成形过程中聚合物熔体壁面滑移的研究[D].上海:东华大学, 2016.
Wang Chun. Research on wall slip of polymer melt in spinning process[D].Shanghai:Donghua University, 2016.
[10] Gupta S, Uday V, Raghuwanshi A S, et al. Simulation of blow molding using Ansys Polyflow[J]. Apcb Proced, 2013,5:468-473.

