山地风电场采用柔性直流输电的WNN控制
闫 婧,王灵梅
(山西大学自动化系,太原 030013)
对式(1)施以式(2)所示的dq坐标变换[7]
风电具有随机性和波动性,且一般远离负荷,山地风特点尤其显著。传统的风电场采用交流输送,而在能量传输过程中,因交流输电系统的同步性、输电稳定性、输电效率等技术瓶颈问题,交流输送方式已越来越不能完全满足需求[1-2]。VSC-HVDC输电系统能够独立控制其传输的有功功率和无功功率并实现系统的潮流反转,因此非常适合应用于可再生能源并网、孤岛供电和向无源网络供电等领域[3]。
传统的MMC柔性直流输电矢量控制策略包括内环电流控制和外环电压控制[4],采用的是双闭环PI控制方式。在仿真过程中,常规的PI控制存在着参数整定不良和系统运行性能欠佳的缺点,且面对复杂的运行工况时,不能随工况扰动而自动调节,因此对于波动性和随机性较大的山地风柔性直流输电系统,很难保持较好的控制效果。小波神经网络(WNN,wavelet neural networks)是将小波理论和神经网络相结合的一种智能控制方法,通常简称为小波网络,其能够有效地通过伸缩以及平移的方式提取信号的局部特征,并且在提取的基础上进行多尺度分析[5]。
利用小波神经网络能逼近任意非线性函数的特点[6],将小波神经网络应用于柔性直流输电中的外环电压控制。因此,本文首先分析了MMC的基本结构和工作原理,根据其数学模型,以某山地风电场为背景,对该风电场的柔性直流输电提出了小波神经网络控制方法,并以10电平的MMC为例,在PSCAD/EMTDC软件中建立了仿真模型,结合Matlab/Simulink中的小波神经网络控制器,完成了整个系统的仿真验证。
1 MMC-HVDC工作原理
1.1 MMC的模型
MMC-HVDC的系统接线如图1所示,三相模块化多电平换流器(MMC)拓扑结构及子模块(SM)结构如图2所示。
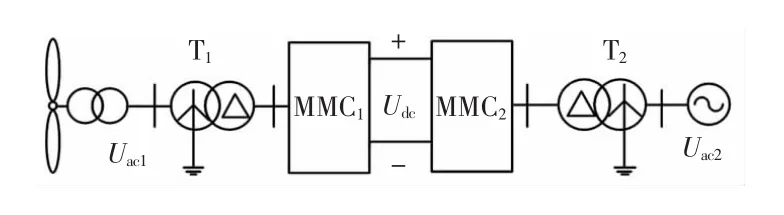
图1 MMC-HVDC系统接线图Fig.1 Configuration of MMC-HVDC system

图2 MMC的拓扑结构Fig.2 Topological structure of MMC
一个换流器有6个对称的桥臂,每个桥臂包含一个电抗器L0和N个子模块,每一相的上下两个桥臂组成一个相单元。2个IGBT与二极管的反向并联单元,再加上一个电容,共同构成一个子模块。子模块输出的2个电平由2个IGBT的工作状态决定。子模块的工作状态如表1所示。每相上下桥臂间串入的电抗器L0用于抑制三相桥臂间产生的环流。
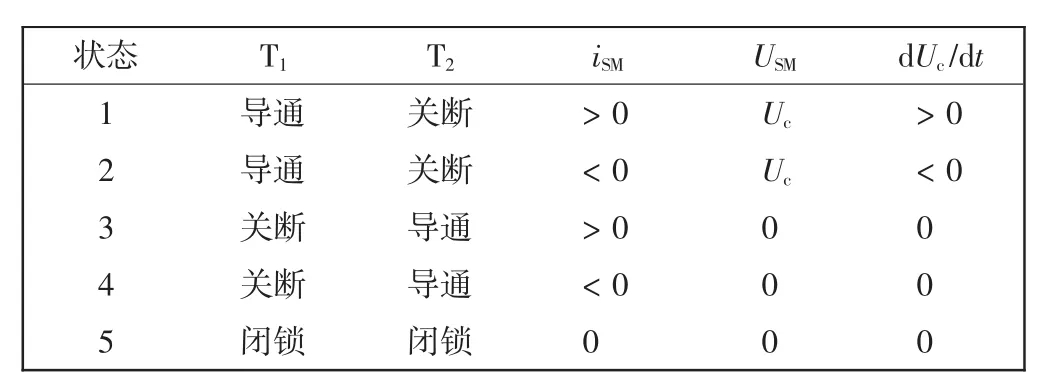
表1 子模块的工作状态Tab.1 Operative mode of submodule
对一个相单元中的上、下桥臂分别应用基尔霍夫电压定律,并表示为三相形式,由图2可得abc坐标系下的数学模型为
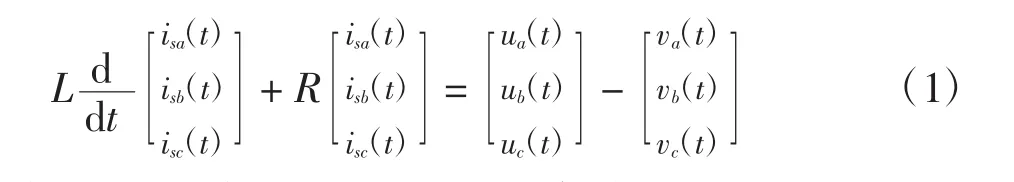
对式(1)施以式(2)所示的dq坐标变换[7]
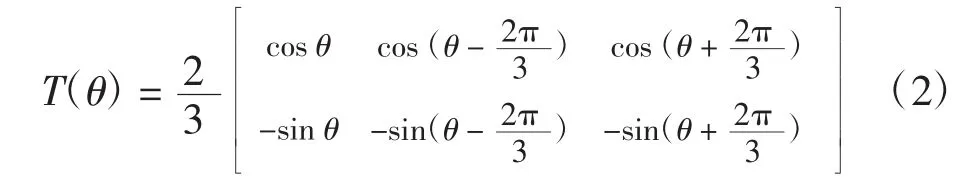
可得到dq旋转坐标系下的数学模型如下

其中:ud、uq分别为dq坐标系下的电网电压分量;vd、vq分别为dq坐标系下的换流器交流侧电压分量;isd、isq分别为dq坐标系下的电网电流分量;ω为旋转角速度;R为三相交流等效电阻;L为交流等效电抗;Udc为直流侧电压。
在式(2)所示的dq变换下,稳态时取d轴方向为电网电压的矢量方向,则有uq=0,MMC交流侧送入换流器的有功功率P和无功功率Q可表示为

1.2 MMC柔性直流输电系统的控制原理
矢量控制包括内环电流控制和外环电压控制。其中,内环电流指令值由外环电压控制器根据有功功率、无功功率和直流电压等指令值的计算得到,通过调节换流器的输出电压参考值udref和uqref,在内环控制下,dq轴电流能够快速跟踪其指令值idref和iqref。内环电流控制器设计如下:
将式(3)改写为如下形式
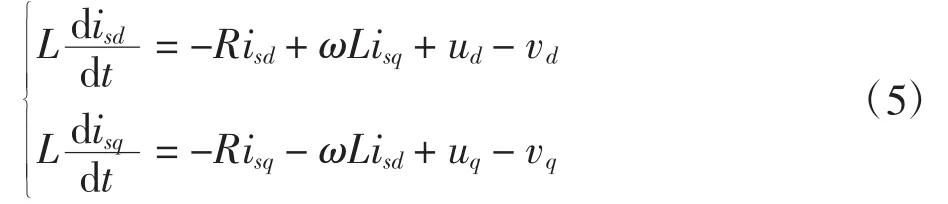
式(5)表明,dq 轴电流除受 ud、uq的影响外,还受电流交叉耦合项ωLisd、ωLisq和电网电压的影响。因此,为消除dq轴之间的电流耦合和电网电压扰动,设计内环电流解耦PI控制器如下
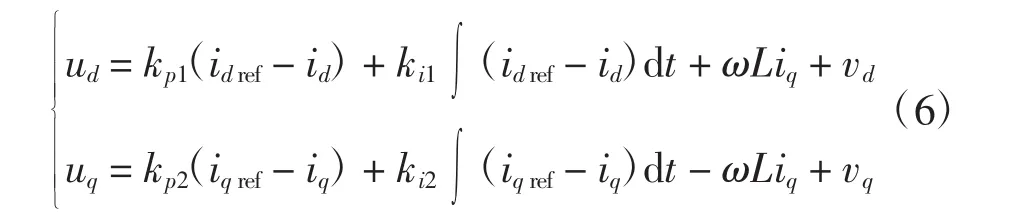
为了保持系统的稳定运行,本文采用定直流电压控制,因此根据直流电压参考值可得到正序d轴电流参考值,其本质是差值控制,具体如式(7)所示

而负序电流的参考值则设置为0,以此实现抑制负序电流、防止电力电子器件过电流的目的。
2 WNN控制系统的建立
2.1 WNN控制原理简介
WNN由输入层、隐含层和输出层组成,其中神经网络隐含层的激励函数由小波函数替代传统函数,相应的输入层到隐含层的权值及阈值分别由小波函数的伸缩系数和平移系数代替[8]。本文使用的是三层前向神经网络,假设输入层神经元个数为m,隐含层为i,输出层为n,其小波神经网络结构如图3所示。

图3 小波神经网络结构图Fig.3 Wavelet neural network structure diagram
本文选用Mexican-Hat小波函数作为激励函数,其实质是Gaussian函数的二次导数,即

其中:Ψ(jx)表示从信号函数 φ(t)得到的小波函数族;X=[x1,x2,…,xm]表示输入向量;ai=[a1,a2,…,ai]和 bi=[b1,b2,…,bi]分别表示小波函数的伸缩和平移系数。bi的改变使小波函数移动,从而具有了时域局部化的特性,不同的值对应不同的时间值。ai的改变使小波函数伸缩,从而具有了频域局部化的特点。Vmi表示输入层节点和隐含层节点之间的权值,Win表示隐含层节点和输出层节点之间的权值。在小波神经网络控制系统中,权值、平移参数和伸缩参数都是待训练的网络参数。
2.2 WNN外环电压控制系统的设计
双环控制策略包含内环电流控制和外环电压控制,为提高系统响应速度,改善动态性能,本文将BP神经网络与外环电压控制相结合,利用小波网络的函数逼近能力,克服传统PI控制的不足。小波神经网络能够根据被控系统的要求,对PI控制器进行调整,输出层对应PI控制器的kp和ki。
将式(7)用增量式数字PI控制表达为
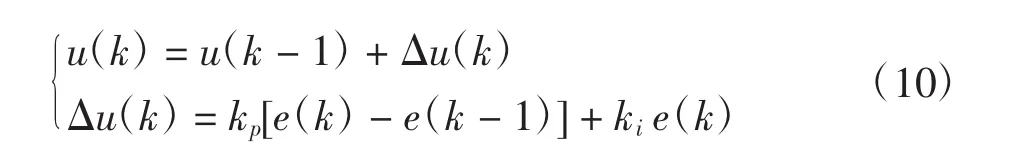
上式还可改写为
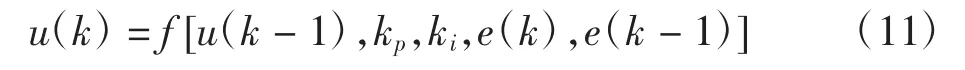
则根据图3,输入层的输入为
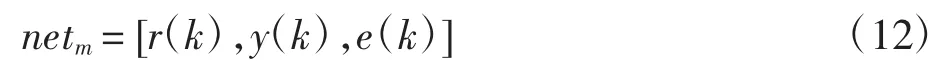
隐含层第i个节点输入和输出分别为

输出层的输入、输出分别为
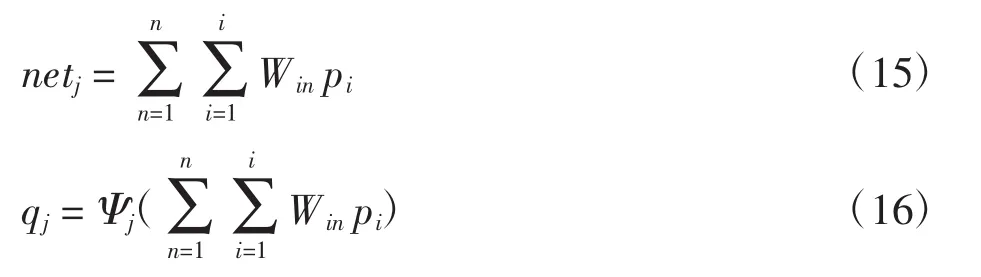
系统的最终误差函数为

对于待训练的网络参数,本文选择BP学习算法的梯度下降法[9]来进行修正,各自的修正公式如下

其中:αi为修正系数,每次循环时,按上述公式调整网络参数,直到E小于某一设定值,具体的网络学习过程如图4所示。
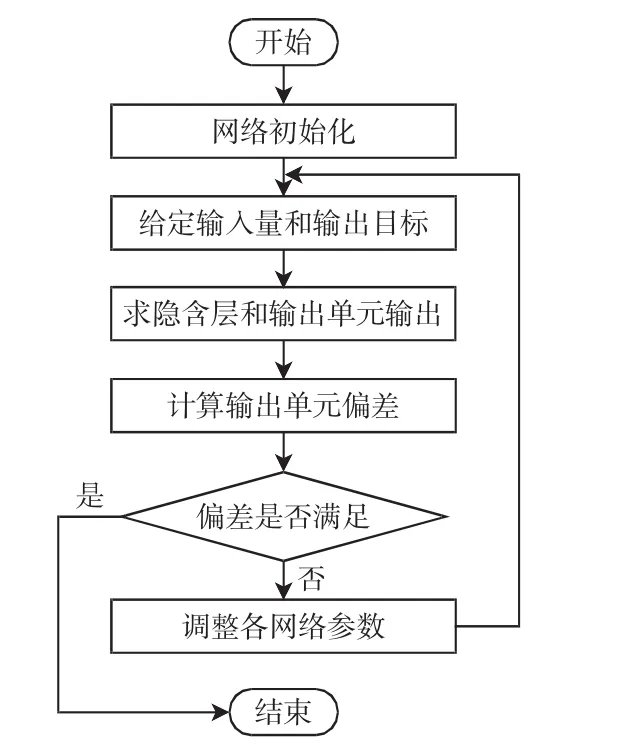
图4 BP神经网络学习过程Fig.4 Learning process of BP neural network
2.3 山地风电场柔性直流输电的WNN控制系统
针对被控系统的运行要求,小波神经网络对PI控制器的kp和ki进行优化调整,直到系统的目标误差函数值达到某一限定值。外环电压PI控制器的参数kp和ki作为神经网络输出层的神经元对应的参数,控制系统结构如图5所示,所设计的小波神经网络结构为3-5-2,即输入层、隐含层和输出层的神经元个数分别为 3、5、2。
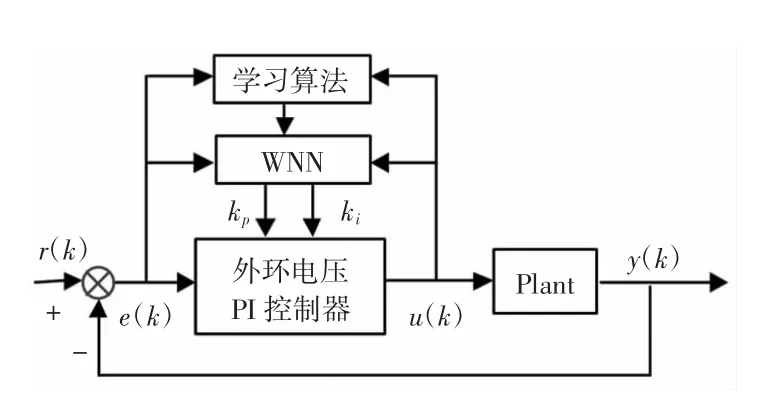
图5 WNN控制系统Fig.5 WNN control system
3 仿真验证
为了验证上述所设计的控制器的正确性和有效性,在PSCAD/EMTDC软件中建立如图1所示的系统,结合Matlab/Simulink中的小波神经网络控制器,对整个系统进行仿真验证,PSCAD/EMTDC与Matlab/Simulink的连接[10]本文不再赘述。系统主要运行参数如下:两端交流系统的额定电压为220 kV,系统阻抗值为7.36 Ω,换流变压器采用Ynd接法,T1与T2的变比分别为210/230 kV和230/220 kV,变压器漏抗为0.2 pu,MMC的单个桥臂子模块数为10,子模块电容为4 600 μF,桥臂电感为4 mH,直流母线电压为400 kV,直流功率P=400 MW,线路采用双极电缆,长度为100 km。系统仿真时间为5 s,在t=4 s时刻,模拟采用定直流电压控制情况下,由于风功率发生突变,导致MMC有功功率最低跌至0.2 pu的情况。仿真结果如图6所示。
如图6所示,图6(a)为定直流电压控制模式下的MMC 直流电压,图 6(b)和图 6(c)分别为 MMC 有功功率和MMC交流侧a相的电流,图6(d)为有功功率的误差百分比。由图6可见,当风速发生突变,有功功率发生波动时,直流电压保持不变,在WNN控制下,误差迅速减小到目标范围之内,随着小波神经网络对网络参数的学习和整定,系统参数具有更好的动态响应,超调小,减小了由于风功率的波动对系统稳定性的影响。

图6 仿真结果图Fig.6 Simulation waveforms
4 结语
本文通过对双环控制器的外环电压控制器进行改进,将传统的PI控制与小波神经网络控制相结合,并以某山地风电场为背景,对该风电场的柔性直流输电采用小波神经网络进行控制。使用BP学习算法的梯度下降法,利用小波网络的函数逼近能力对网络参数进行学习和训练,进而调整PI的比例和积分系数,实现外环电压的控制,克服传统PI控制超调大的不足,具有更好的动态特性,对大规模可再生能源并网具有指导性作用。
[1]田园园,廖清芬,刘涤尘,等.基于VSC-HVDC的风电分散并网下垂控制策略[J].电力系统自动化,2016,40(3):103-109.
[2]任爱平,李旭霞,胡迎迎.山西电网风电出力特性及消纳形势分析[J].山西电力,2016(3):41-44.
[3]FLOURENTZOU N,AGELIDIS V G,DEMETRIADES G D.VSC-based HVDC power transmission systems:an overview[J].IEEE Trans on Power Electron,2009,24(3):592-602.
[4]刘 昇,徐 政,唐 庚,等.VSC-HVDC机电暂态仿真建模及仿真[J].电网技术,2013,37(6):1672-1677.
[5]郑小洋.小波神经网络及其应用[D].重庆:重庆大学,2003.
[6]罗 兵,章 云,黄红梅.小波神经网络与PID相结合的负荷频率控制[J].电力自动化设备,2006,26(1):25-29.
[7]管敏渊,徐 政.模块化多电平换流器型直流输电的建模与控制[J].电力系统自动化,2010,34(19):64-68.
[8]王建平.小波神经网络的内模控制在再热气温控制中的应用[D].北京:华北电力大学,2007.
[9]韩立群,王志新,叶 斌.智能控制理论及应用[M].北京:机械工业出版社,2007:105-114.
[10]乐 健,胡仁喜.PSCADX4电路设计与仿真从入门到精通[M].北京:机械工业出版社,2015:478-486.

