机场能耗的时间序列混合预测方法

王 力，张 超

（中国民航大学电子信息与自动化学院，天津 300300）

时间序列概念起源于1927年，中国在20世纪70年代末到80年代中后期才开始深入研究和应用。传统时间序列分析方法多基于统计学基础，如自回归移动求和平均（ARIMA）模型和条件差异方差（ARCH）模型。支持向量机（SVM）最早是在20世纪60年代依据SLT中结构风险最小化原则提出的一种机器学习方法，能够极大地提高学习机的适应能力，即使由有限数据得到的判别函数对独立测试集仍能够得到较小的误差[1]。其中传统时间序列对线性数据有较好的处理能力，SVM在解决小样本、非线性以及高维模式识别问题中又有许多特有的优势，并能够推广到函数拟合等其他机器学习问题中，如梅倩[2]提出将LS_SVM应用到时间序列中以提高预测精度，通过LS_SVM对原始数据进行预处理，用筛选后的时间序列应用各种处理方法进行预测，也得到了较好的预测精度。上述研究在一定程度上解决了单一模型预测精度不够的问题，泛化能力较好，但在稳定性和能耗异常预测中仍有不足。

本文提出一种基于混合模型的时间序列建模和预测方法，首先对传统的时间序列模型进行改进，得到混沌时间序列预测模型[3]，从而增强时间序列对非线性数据的预测能力，然后将预测残差作为支持向量机SVM的输入，对残差进行处理，进一步增强对非线性数据的处理能力。最后分别采用改进后的混沌时间序列模型、SVM和时间序列混合预测模型3种方法对天津滨海国际机场的能源消耗情况进行建模和预测，实验仿真结果表明，所提出的混合时间序列模型的建模精度和预测效果优于其他模型。

1 研究方法

1.1 混沌时间序列预测模型

时间序列由于其影响因子的不同，可能呈现周期性或非周期性特点，还有一些时间序列数据表现出混沌的特点，因此在对时间序列问题进行分析之前要先对时间序列的性质进行判别[4]。本文采取目前常用的Lyapunov指数法，可以反映混沌系统对初始条件的依赖性，若Lyapunov最大指数大于0，说明时间序列呈现出来的特点是混沌性的。常用的计算方法包括小数据量法、WOLF方法和BBA方法，本文采用WOLF方法对时间序列的Lyapunov指数进行计算。

1.1.1 混沌时间序列的判定

1）设时间序列的延迟时间为τ，观测数据样本总数为n，构建新序列的嵌入维度为m，则相点数为N=n-（m-1）τ，可将n个样本值重构为m×N维的新矩阵，重构后的相点可表示为

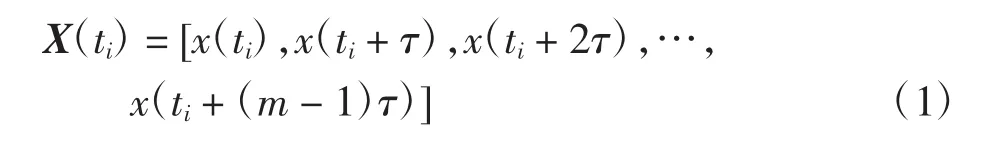
其中：i=1，2，…，N。

2）以第 1 个相点 X（t0）为起点，在相点集合 X（t）中寻找和X（t0）距离最接近的相点X（t）j为终点构建一个初始向量。起始点之间的欧氏距离记为L（t0）=‖X（t）0-X（t）j‖m，m为嵌入维度，增长率均值为Lyapunov指数的估计值。

3）设k为时间步长，t1=t0+k为t0向前递推k步得到的一个新向量，按照第2步中的方法定义这个新的向量对应的距离函数为L（t1），则在对应时间内系统的增长率为

4）重复第2步和第3步，直到计算出所有相点的欧氏距离和对应增长率，然后取所有增长率的平均值为Lyapunov指数的估计值，即

1.1.2 延迟时间的选取

在重构相空间过程中其结构的好坏直接影响后续预测过程的准确程度，所以延迟时间τ是时间序列重构的重要参数，计算延迟时间的方法主要有最小互信息法、平均位移法、（去偏）复自相关法、重构展开法等，其中最小互信息法的应用最为广泛，该方法选取时间序列的第1个最小互信息值作为优化的延迟时间[5]。

首先需要构造一个包含时间序列的非线性特征的互信息函数I，定义由bj在时间序列B中发生的信息而得到关于ai在时间序列A中发生的信息，称为序列A与序列B之间的平均互信息，其函数关系为

其中：A，B代表两个不同的时间序列，如果要在同一个时间序列内部构造平均互信息函数，可假设时间序列[ai，bj]=[x（t），x（t+ τ）]，则式（4）、式（5）可写为

在计算过程中可将样本空间划分成若干模块，然后通过统计各模块中的点数来计算其概率值，一般可选取延迟矢量之间互信函数的第1个极小值点作为延迟时间τ。

试验过程中以石英砂作为试验矿样，细磨试验前将其破碎至0.2mm以下，其粒度组成如表1所示。试验用石英砂的矿石密度为2.65g/cm3，莫氏硬度为7，调浆后浓度控制在45%左右，试验时间控制在0～35min以内，在不同固定时刻进行采样，并用粒度仪分析产品粒度（以-45μm含量作为评价指标）。

1.1.3 最佳嵌入维数的选取

时间序列重构过程中另一个重要的影响参数就是嵌入维度，若选取的嵌入维度过小，原本距离较远的某点可能会变得比较近，影响Lyapunov指数的判断；反之，若选取的嵌入维度过大，在理论上可行，但实际应用中需要更多数据并增加了计算任务量，而且噪声干扰也会变得更加显著，反而影响后续的预测精确度。因此选取一个合适的嵌入维数不仅对时间序列建模有重要意义，也为预测器的阶数选择提供重要依据。通常选取嵌入维度的计算方法主要有奇异值分解法、伪邻近点法（FNN）及饱和关联维数法[6]。本文采用伪邻近点法（FNN）。

伪临近点法（FNN）是基于吸引子空间的几何结构是否被完全打开的一种方法。若所选嵌入维数较小，相当于吸引子投影到低维空间，会使得原本距离较远的点变成邻近点，因而产生了“伪邻近点”，因此可通过计算伪邻近点的比例大小来选取最优嵌入维数。设重构延迟矢量Xi的邻近点为Xj，由欧式空间理论得到Xi和Xj之间的距离为R（im）=‖Xi-Xj‖m，当维数增大至m+1维时距离为R（im+1），若R（im+1）比R（im）大很多，可以认为Xi和Xj是伪近邻点。在具体计算时，可以根据实际情况选取临界值（r一般10≤r≤50），并判断r是否满足以下不等式

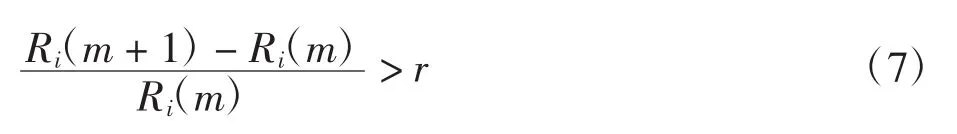
若满足，则Xi和Xj是伪临近点。本文在计算时取r=15，m从2开始取值依次增加，直到伪临近点的数量不再随m值的增大而减少（即此时伪临近点的比例可视为最低），此时的m值即为最佳嵌入维度。

1.1.4 一阶加权局域法预测模型

选取合适的延迟τ和嵌入维度m之后，便可建立一个合适的预测模型来对时间序列进行预测，目前全局预测法、局域预测法、自适应预测法和局域自适应预测法等均为主流的预测方法[7-8]。通过大量已知的仿真结果，一般认为预测效果由差到好依次为：全域法、局域法、加权局域法，本文选用一阶加权局域法来对机场用电量进行预测。

将相空间轨迹的最后一个相点XK作为参考点，把距离此参考点最近的若干相点作为相关参考点，计算各相关参照点到参考相点XK的距离，找出XK的局域参考向量集，设点到 XK点的距离为di，dm是其中的最小值，则可定义点的权值为

其中：i=1，2，…，q；c为常系数，一般取作 1。一阶局域线性模型拟合成为

其中：i=1，2，…，q；e=（1，1，…，1）T；a、b 为待定系数。当嵌入维数为m=1时，为满足平方误差最小原则，可用加权最小二乘法，即

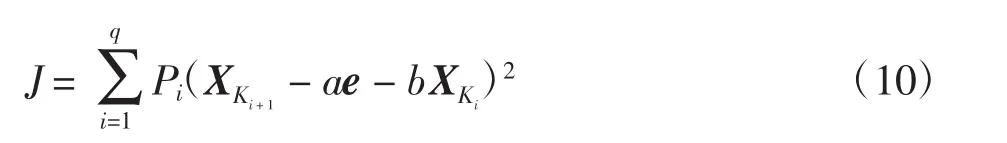
将J分别对a、b求偏导并使其为0，得

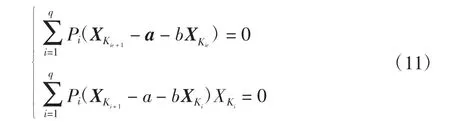
1.2 时间序列混合预测模型

时间序列包括线性自相关结构和非线性结构两部分，即

其中：At代表时间序列的线性部分；St代表时间序列的非线性部分。首相利用混沌时间序列预测模型对线性自相关部分At建模，其所剩的残差部分为

然后用SVM对残差部分进行建模。由以式（14）得到一个残差序列 E（t）=[et-n-m+1，et-n-m+2，…，et-1，et]，构建如下输入矩阵与输出矩阵，即

其中：m为支持向量机输入重构的最佳维数。传统SVM预测模型为

其中：αi和为拉格朗日乘子；K为核函数，一般选取

作为SVM预测模型的核函数[9]。

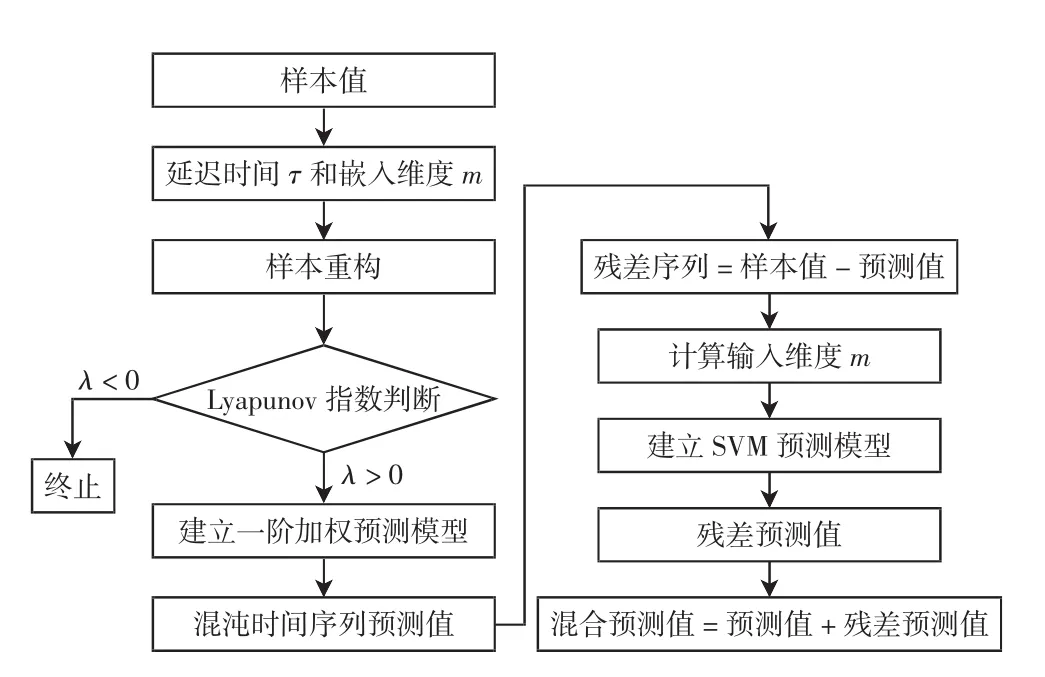
图1 混合预测模型流程图Fig.1 Flow chart of hybrid prediction model

2 天津机场耗电量时间序列实例分析

将天津滨海国际机场2014年1月至2015年12月共104个周耗电量作为实验样本，如图2所示。机场用电能耗影响因素复杂，天气情况、航班进出港情况、人群的流动因素等都会对某一时段的用电量造成较大影响，且变化规律复杂。因为周用电量很有可能是一个混沌的时间序列，首先对其混沌性进行判断，由1.1.1中提到的方法计算机场能耗时间序列的最大Lyapunov指数，结果为λ=0.091 3＞0，因此可以认为这个时间序列是混沌的。由前文介绍的重构理论X（t）i=[x（t）i，x（ti+τ），x（ti+2τ），…，x（ti+（m-1）τ）（]i=1，2，…，N），用最小互信息的方法求得机场能耗数据时间序列的最佳延迟时间为τ=5，如图3所示。继而由伪临近点法得到重构空间的最佳维数m=4，如图4所示。重构后得到88个4维向量即88重构样本。

图2 机场实际能耗数据Fig.2 Airport energy consumption data

图3 互信息法选取延迟时间Fig.3 Mutual information method for delay time selection

针对所选取的机场能耗数据确定出的相空间时选取的延迟时间为5，嵌入维数为4。对机场能耗数据进行重构后，根据1.1.4中的理论建立加权一阶局域预测模型来对这重构后的88个数据进行预测，混沌时间序列模型预测的结果如图5所示，预测的绝对误差（样本值-预测值）和相对误差（样本值-预测值）如图6和图7所示。

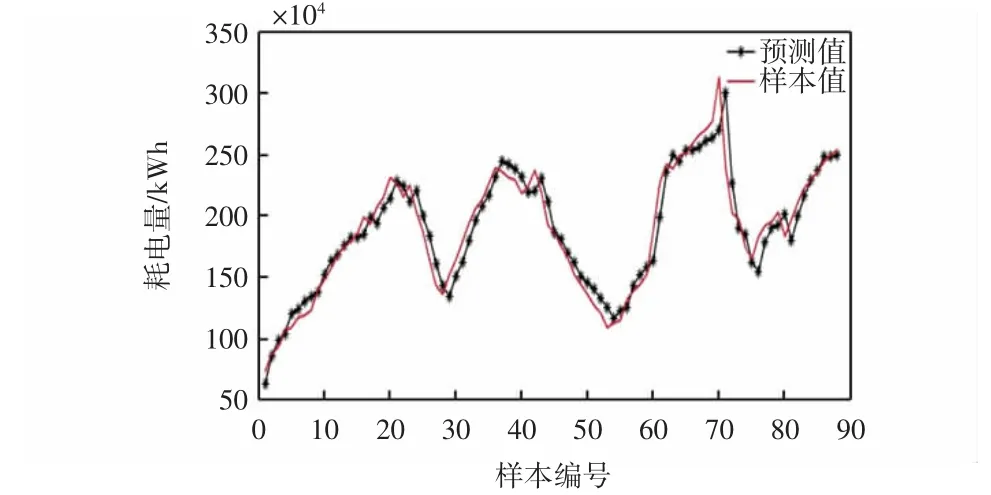
图5 样本值与混沌时间序列模型预测值Fig.5 Sample value and chaotic time series prediction value

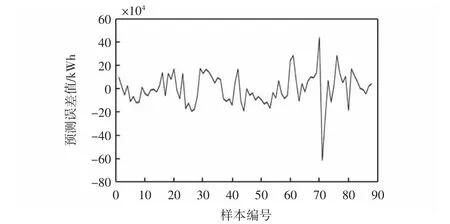
图6 模型预测绝对误差Fig.6 Absolute error of model prediction

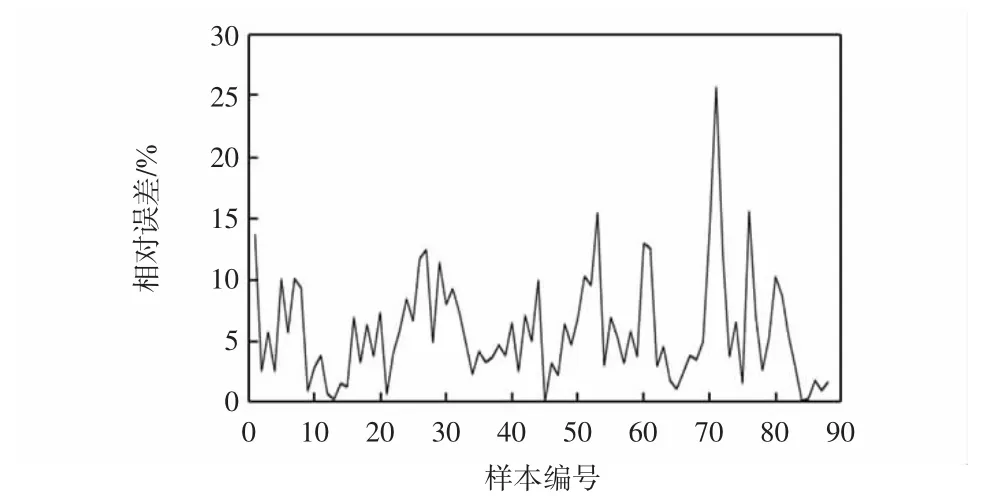
图7 模型预测相对误差Fig.7 Relative error of model prediction

由混沌时间序列建模的预测结果可以看出模型预测的相对误差基本上在0～10%之间，其中有一个点的预测结果偏离较大，预测误差值为-61.41×104kWh（25.67%），明显高于平均绝对误差9.55×104kWh（5.46%）。这是由于时间序列的局限性造成的，其预测结果仅能依据历史数据而不能考虑到外界条件的变化造成的较大的非线性偏差。为得到更好的预测结果，保留该异常点，这也是将预测过程拆分成两部分的好处，可借助SVM对非线性小样本数据良好的预测能力，最大程度地弥补混沌时间序列模型预测过程中产生的非线性误差，从而达到模型改进的目的。

图8 SVM模型误差预测Fig.8 Error prediction of SVM model

图9 样本值与混合模型预测值Fig.9 Sample value and hybrid model prediction value

若以SVM模型单独进行预测，效果也是不尽理想的，预测的绝对误差平均值为9.88×104kWh，平均相对误差为6.34%，其预测结果如图10所示。

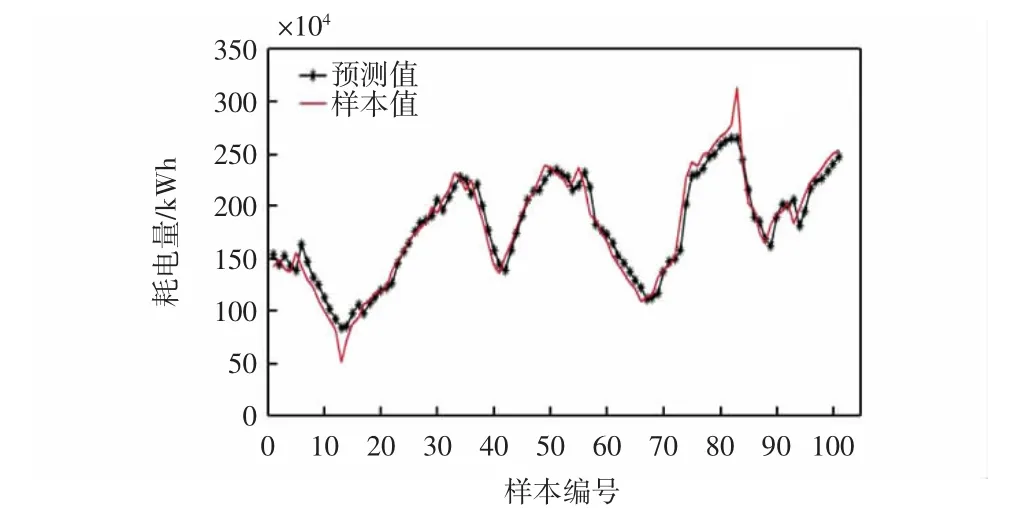
图10 样本值与SVM模型预测值Fig.10 Sample value and SVM model prediction value

3 预测结果与分析

采用支持向量机预测模型、混沌时间序列（一阶加权局域模型）和混合时间序列预测模型分别对天津机场2014年1月至2015年12月中的104周的电能消耗时间序列进行预测，各预测模型的预测结果平均绝对误差（样本值与预测值之差的绝对值的平均值）和平均相对误差（平均绝对误差/样本值）如表1所示。

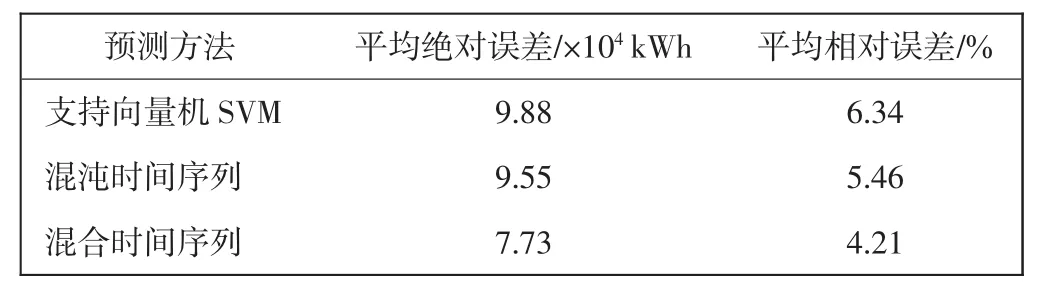
表1 时间序列预测性能比较Tab.1 Time series prediction performance comparison

从表1可以看出混合时间序列预测模型的预测精度要明显好于单一的混沌时间序列模型和单独的SVM预测模型。

4 结语

提出了一种混沌时间序列和支持向量机相结合的预测方法。混沌时间序列主要用于对时间序列的线性部分进行预测，预测结果与样本值的非线性残差部分由支持向量机进行预测。仿真结果表明，混合后的预测模型可以明显提高预测精度，其预测效果好于单独的混沌时间序列预测模型和SVM预测模型。该混合模型展现出了更好的适应能力，为能耗时间序列预测建模提供了一种新方法，针对复杂、影响因素多变的能耗时间序列有较好的应用推广能力。

[1]丁世飞,齐丙娟,谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报,2011,40(1):5-9.

[2]梅 倩.LS-SVM在时间序列预测中的理论与应用研究[D].重庆:重庆大学,2013.

[3]张金良,谭忠富.混沌时间序列的混合预测方法[J].系统工程理论与实践,2013,33(3):763-769.

[4]AWREJCEWICZ J,KRYSKO A V,ZAGNIBORODA N A,et al.On the general theory of chaotic dynamics of flexible curvilinear Euler-Bernoulli beams[J].Nonlinear Dynamics,2015,79(1):11-29.

[5]田中大,高宪文,石 彤.用于混沌时间序列预测的组合核函数最小二乘支持向量机[J].物理学报,2014,63(16):66-76.

[6]王 妍,徐 伟,曲继圣.基于时间序列的相空间重构算法及验证(一)[J].山东大学学报：工学版,2005,35(4):109-114.

[7]MIERCZYNSKI J. Estimates for principal Lyapunov exponents: A survey [J]. Nonautonomous Dynamical Systems, 2014, 1(1):137-162.

[8]穆文瑜,李 茹.基于K-Means聚类的瓦斯浓度预测[J].计算机应用,2011,31(3):702-705.

[9]章永来,史海波,周晓锋,等.基于统计学习理论的支持向量机预测模型[J].统计与决策,2014(5):72-74.