冷弯薄壁C型钢绕强轴偏心受压构件的极限承载力
程睿+刘松松+黄宗明+石宇+崔佳+李哲刚

摘 要:冷弯薄壁型钢结构多采用有效截面法对构件承载力进行计算,该方法计算繁杂且未考虑构件的畸变屈曲性能。直接强度法采用全截面计算各类参数,能够考虑各种单独屈曲模式及其相关屈曲对构件稳定性能的影响,但目前该方法并不能应用于压弯构件。对冷弯薄壁C形钢绕强轴偏压构件的稳定性能进行参数分析,探讨了构件长度、偏心距、腹板高厚比、翼缘宽厚比和卷边高厚比等因素对构件承载力的影响规律。结合有限元分析结果,基于轴压构件和纯弯构件的直接强度法公式,提出了冷弯薄壁型钢绕强轴偏压构件的极限承载力计算方法。
关键词:冷弯薄壁型钢;偏心受压;极限承载力;直接强度法
中图分类号:TU392.1 文献标志码:A 文章编号:1674-4764(2018)01-0009-08
Ultimate strength of C-shaped cold-formed steel members in compression and major axis bending
Cheng Rui1a, 1b, Liu Songsong1b,Huang zongming1a, 1b,Shi Yu1a, 1b,Cui Jia1a, 1b,Li Zhegang2
(1a. Key Laboratory of New Technology for Construction of Cities in Mountain Area, Ministry of Education;2. School of Civil Engineering, Chongqing University, Chongqing 400045, P. R. China;
3. CMCU Engineering Co. Ltd, Chongqing 400039, P. R. China)
Abstract:Effective section method (ESM) is widely used in the design of cold-formed steel structures. However, the influence of distortional buckling of members was hot considered. A new method for the load carrying capacity of cold-formed steel members, direct strength method (DSM), can effectively estimate the ultimate strength for local, distortional buckling and interactive buckling. However, it is not used for beam-columns. The stability behavior of C-shaped cold-formed members eccentrically compressed around the major axis was analyzed. The effects of Length of member, eccentricity and width-thickness ratio of webs, flanges and edge stiffeners on ultimate strength of members were examined in this study. A calculation method of ultimate strength was proposed based on the original DSM axial compression/bending formulas and the finite element analysis results.
Keywords:cold-formed steel members; eccentrically compressed; ultimate strength; direct strength method
目前,針对冷弯薄壁型钢构件承载力的计算主要有两种方法,一是各国规范中普遍采用的有效截面法,该方法主要来自Winter[1]和Mulligan等[2]的研究成果,提出了弹性局部屈曲临界应力及有效宽度的计算公式;另一种是直接强度法,由于有效截面法不能考虑构件的畸变屈曲性能,而直接强度法则能分别考虑各种单独屈曲模式及其相关屈曲对构件稳定性能的影响,且避免了繁杂的有效截面计算,成为目前研究的重点。
目前,对冷弯薄壁型钢受压构件受力性能的研究[3-6,11]主要以轴心受力构件为主,对于常见的压弯构件性能的系统性研究成果并不多[7-10]。虽然,现有研究针对偏压构件承载力计算提出了建议,但大多是围绕有效截面法开展的分析讨论,对直接强度法在偏压构件中的应用关注较少[10-12]。由于直接强度法在压弯构件中的应用研究还处于起步阶段,目前的规范并没有将其纳入其中。因此,需进一步系统研究压弯构件的稳定性能,特别是构件的畸变屈曲性能。
笔者对冷弯薄壁C形钢绕强轴偏压构件的稳定性能进行变参数分析,以考察构件的失稳模式和极限承载力,提出基于直接强度法的冷弯薄壁型钢绕强轴偏压构件的承载力计算方法。
1 冷弯薄壁C型钢偏压构件计算模型
对比验证试验
1.1 试件样本
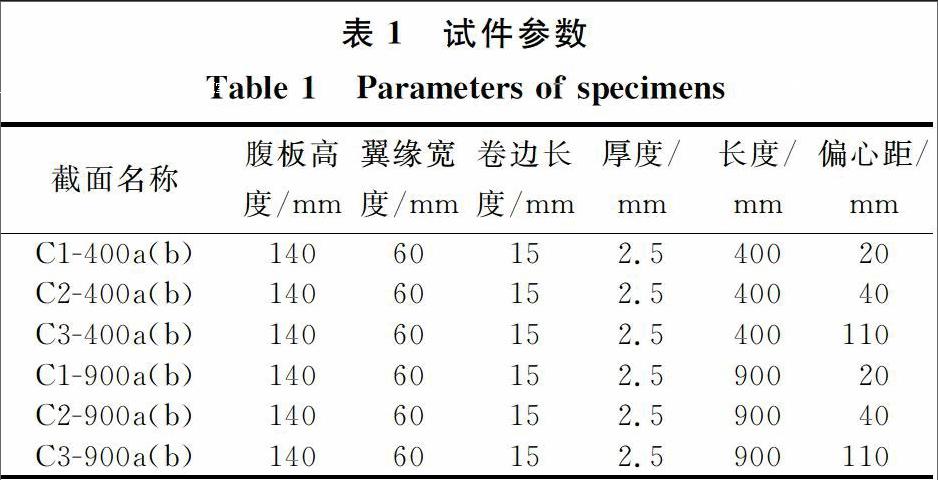
选取不同几何参数的C型钢进行绕强轴偏压稳定性能试验,试件总数共计12根。截面腹板高140 mm,翼缘宽60 mm,卷边长15 mm,厚度为2.5 mm。为了提供不同偏心距荷载作用下的破坏模式和极限承载力的对比验证样本,试验加载偏心值分别取20、40和110 mm,试件长度分为400和900 mm。试件的具体参数如表1所示。所有参数相同的试件加工两件,以a、b区分,其目的是通过相同试件试验的相互验证确保试验结果的可靠性。所有试件均参照文献[11]提出的方法对初始缺陷进行测量。试件所用钢材的材料属性通过标准试件拉伸试验确定,材性试验结果列于表2。endprint
1.2 试验加载装置及加载制度
试验加载装置如图1所示,试件上下端部支座均为单向刀铰支座,支座端板与试件之间采用文献[10]所采用的围箍装置进行连接,该装置通过调节螺杆可实现不同偏心距的加载。试件的应变片布置如图2所示,为校正加载偏心距的大小,分别在试件1/4和3/4高度位置处布置有应变片,以此反算实际偏心距的大小;同时在刀铰支座板上对应于荷载作用线的位置布置位移测点,对试件的轴向变形进行测量,以获得试件加载全过程的荷载与变形曲线。
试验加载采用分级加载,初始阶段每级荷载增量不超过预估极限荷载的5%,当荷载达到预估极限荷载的80%左右时,减小荷载增量至预估极限荷载的2.5%,当荷载开始减小时,可以认为试件达到极限承载力。之后进入卸载阶段,继续测量采集下降段数据,直到试件变形明显或持荷能力迅速下降时停止试验。
1.3 试验结果
图3为试件典型的失稳破坏模式。通过试验观察到,试件的变形由腹板的波形凸曲、翼缘卷边组合体的转动组成,腹板和翼缘的变形往往出现在同一柱高处。当偏心距为20 mm时,试件的破坏模式为以腹板局部屈曲为主伴随翼缘畸变变形(WLB,其屈曲时的波长约为100 mm);当偏心距为40 mm和110 mm时,试件发生以畸变屈曲为主的破坏现象(FDB,其屈曲时的波长约为300 mm)。典型的偏心受压试件荷载轴向位移曲线见图4,图中可以看出,长度为900 mm的试件在到达极限承载力时的变形较400 mm的试件更大,且荷载在峰值后下降更快,说明较长试件的失稳破坏伴随有整体屈曲的影响,而较短试件在发生破坏时,整体屈曲的特征并不显著。
2 有限元分析模型的验证
有限元计算采用大型通用软件ANSYS,计算单元采用弹塑性壳单元Shell181。模型依据实测尺寸建立,边界条件、材料属性以及加载方式均与试验一致。模型采用正方形的网格划分,网格尺寸为10 mm×10 mm。模型中构件的两端建立了与实际的支座板尺寸相同的端板,端板上相应于刀铰的位置即为模型中的约束点和加载点。这部分节点垂直于构件轴向的平动位移均被约束,上端板刀铰位置处节点沿构件轴向的位移也被约束。加载由下往上,荷载以节点荷载的形式施加在下部刀铰位置处的节点上。由于冷弯薄壁型钢截面薄膜残余应力对构件受压性能的削弱作用与弯曲半径处材料屈服强度提高对构件受压性能的增强作用大致相当[13],可以认为二者对构件极限承载力的总体影响效应较小,故有限元分析未考虑残余应力的影响。
图5所示为部分试件失稳破坏模式的对比图,从图中可以看出,试件无论是破坏模式还是变形发生的位置,有限元分析结果与试验的实际情况都一致。表3所列为试件承载力的有限元计算值、试验值以及误差分析,从表中可以看出,有限元分析结果与试验结果比值的最小误差为-2%,最大误差为3%,均值为0.98,标准差为0.048,两者的结果吻合较好。
图6给出这2个试件的试验和有限元的荷载轴向位移曲線的对比图。从图6可知,在达到极限荷载之前,两条曲线的重合度较高,峰值点也基本接近。通过对有限元分析的承载力、破坏模式和荷载位移曲线与试验结果进行对比,表明有限元模型能够较好地模拟构件的实际受力情况,给出一个合理的模拟结果,因此,可以将该模型用于后文的参数分析。
3 冷弯薄壁C型钢绕强轴偏压构件极
限承载力参数分析
冷弯薄壁型钢构件的几何尺寸通常是影响其稳定承载力的主要因素,偏压构件的加载偏心距也会影响到构件的失稳破坏模式。因此,通过变换腹板和翼缘宽度、卷边长度、构件长度及偏心距,对冷弯薄壁C型钢绕强轴偏压构件的失稳模态及承载力进行参数化分析,所选几何参数如表4所示。材料本构模型采用双线性模型,屈服强度为345 MPa,弹性模量取2.06×105 MPa,泊松比取0.3。参数分析结果见表5。后续分析中试件编号规则为:C腹板高度翼缘宽度卷边长度板厚。
3.1 构件长度对构件稳定性能的影响
选取模型C160-60-10-2.5(以腹板局部失稳为主)与模型C160-60-20-2.5(以畸变失稳为主)讨论构件长度对偏压构件稳定承载力的影响,计算结果如图7所示。
结果表明,对于以畸变失稳为主的构件,当构件长度从400 mm增长到1 400 mm时,承载力降低最明显,在计算长度大于1 400 mm之后,承载力下降趋于缓慢。对于以腹板局部失稳的构件,在研究的整个计算长度范围内,承载力随长度的增加而缓慢降低。究其原因,主要是畸变屈曲的半波长度较大,其波长受多种因素影响,当试件长度较短与畸变屈曲半波长接近时,构件支座会对失稳变形的发展起到约束作用,从而提高构件的承载力。而随着构件长度的增加,这种约束效应逐渐减弱,构件的承载力随长度变化的趋势也逐渐趋于缓和。
3.2 偏心距对构件稳定性能的影响
典型的偏心距影响规律如图8所示。从图8可以看出,偏心距对构件承载力的影响显著。当偏心距较小时,随着偏心距增大,构件承载力的降幅较大,之后承载力的降幅逐渐减缓。从表5可以看出,构件的失稳破坏模式也随偏心距增大而发生变化,当偏心距较大时,构件由腹板局部失稳为主的破坏模式转变为畸变失稳模式,即偏心距较大时,构件更容易发生畸变失稳破坏。
3.3 板件宽厚比对构件稳定性能的影响
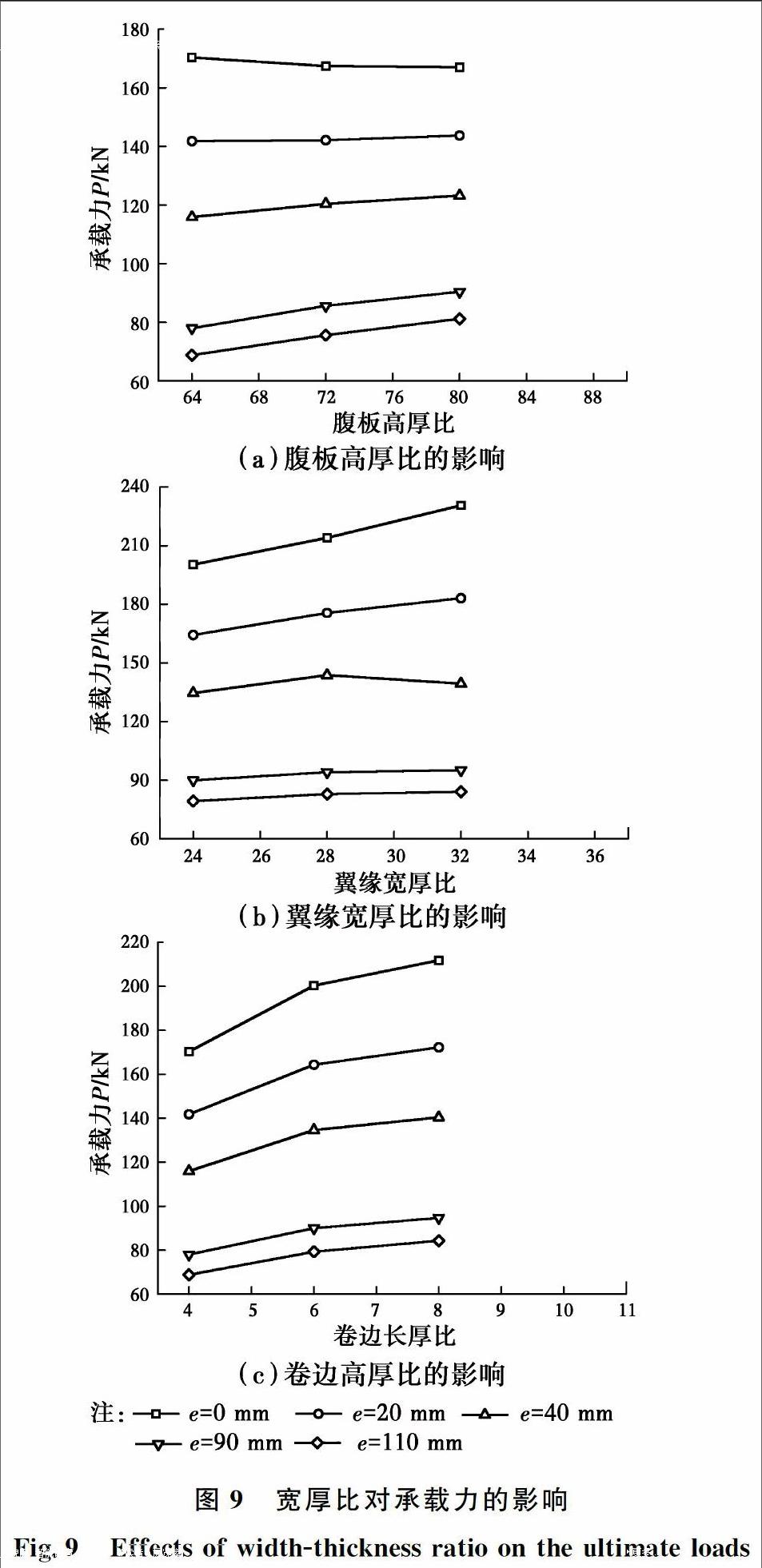
选取长度为1 400 mm构件来研究腹板高厚比、翼缘宽厚比、卷边高厚比与承载力在不同偏心距下的关系,计算结果如图9所示。
1)腹板高厚比 图9(a)所示为腹板高厚比与承载力在不同偏心距下的关系。由图可知,当偏心距为零时,承载力随腹板高厚比的增加有降低的趋势。原因是在于,当构件接近轴压时全截面受压,以腹板局部失稳为主要破坏模式,整体弯曲变形较小,局部失稳受板件高厚比的影响比较明显,高厚比越大越容易失稳,故承载力有所降低。随着偏心距的增大,构件承载力随腹板高厚比的增加而逐渐提高,主要是因为腹板截面的受压区宽度逐渐减小使得腹板板件的稳定承载力有所提高。此外,偏心距增大使得构件截面受拉区扩大,构件在弯矩作用平面外的整体弯扭变形受到限制,从而也提高了构件的承载力。endprint
2)翼缘宽厚比 图9(b)所示为翼缘宽厚比与承载力在不同偏心距下的关系。由图可知,当偏心距较小时,承载力随翼缘宽厚比的增大而显著上升。主要原因在于,此时构件以局部失稳为主要破坏模式,翼缘板件宽厚比的增大使得有效截面增加,因此,承载力会上升。随着偏心距的增大,承载力随宽厚比的增大而上升的趋势逐渐变缓。究其原因,当偏心距较大时,构件以局部屈曲为主控的失稳模式过渡为畸变失稳为主控的破坏模式,在卷边长度不变的情况下,翼缘宽度越大,卷边对其的约束作用越弱,从而使得构件发生畸变失稳的承载力降低;但此时截面受拉区的增加又使得构件的整体刚度增大,这两种对承载力起相反作用的因素相结合使得承载力的变化不再显著,甚至出现降低。
3)卷边高厚比 图9(c)所示为卷边高厚比与承载力在不同偏心距下的关系。从图中可以看出,构件的承载力会随卷边高厚比的增加而增大。主要原因在于,当构件为局部失稳为主控的破坏模式时,卷边高厚比的增加使得有效截面增大,从而提供构件的承载力。当构件为畸变失稳为主控的破坏模式时,卷边高厚比的增加能有效增大卷边对翼缘板的约束作用,限制翼缘板的变形,从而使得构件的承载力提高。
4 构件极限承载力计算方法
目前,规范中普遍采用有效截面法计算构件的极限承载力。该方法需要计算有效截面面积和有效截面模量,随着截面形式复杂化,其计算比较困难,并且该方法基于板件发生局部屈曲对构件承载力的影响而得到,并不能考虑构件的畸变屈曲性能。为了弥补有效截面法的不足,采用全截面计算构件极限承载力的直接强度法越来越受到研究者的重视。目前,直接强度法的研究成果仅适用于轴压或者纯弯受力状态下的简支构件,由于偏心受压构件受力更加复杂,该方法在偏压构件中的应用研究成果还比较匮乏。鉴于直接建立偏压构件的直接强度法公式仍然比较困难,借鉴普钢中对偏压构件寻找P-M关系的思路,基于轴压或者纯弯构件的直接强度法公式,提出适用于冷弯薄壁型钢偏压构件的P-M关系。
4.1 建议公式
1)当构件发生以腹板局部屈曲为主的破坏模式时,P/Pnl与M/Mnl的关系如图10(a)所示,其极限承载力按照式(1)计算。
式中:Pnl、Pnd为根据北美(加拿大)North American specification for the design of cold-formed steel structural members(S136-12)[14]中规定的直接强度法计算公式分别得到的构件在轴压状态下局部失稳和畸变失稳对应的极限承载力。Mnl、Mnd为构件在纯弯状态下局部失稳和畸变失稳对应的极限承载弯矩。
在上述结果中,局部失稳承载力公式计算值与有限元分析值的比值的平均值为0.901,标准差为0.024;对于畸变失稳,平均值为0.903,标准差为0.024。建议公式与有限元分析值吻合较好。
4.2 建议公式适应性校验
建议公式是依据参数分析结果得到的,将试验结果与建议公式计算值进行对比可得,公式计算值与有限元值比值的均值为0.898,标准差为0.084。图11还给出文献[7]和[8]的试验结果与建议公式计算值对比结果,其公式值与有限元值比值的均值为0.774,标准差为0.052。分析结果说明,建议公式可以较好地预测绕强轴偏压构件的局部失稳和畸变失稳时的承载力。
5 结论
对冷弯薄壁C形钢绕强轴偏压构件的稳定性能进行了研究,通过有限元参数分析,探讨了构件长度、偏心距、腹板高厚比、翼缘宽厚比和卷边高厚比等因素对构件承载力的影响规律,得到如下结论:
1)构件的失稳破坏模式随偏心距增大而发生变化。当偏心距较大时,构件由腹板局部失稳为主的破坏模式转变为畸变失稳模式。
2)当构件趋近于轴压时,承载力随腹板高厚比的增加有降低的趋势;随着偏心距的增大,由于腹板受压区宽度的减小和受拉区的约束作用,构件承载力随着腹板高厚比的增加而逐渐提高。
3)当偏心距较小时,承载力随翼缘宽厚比的增大而显著上升。随着偏心距的增大,构件逐渐转向畸变失稳为主的破坏模式,翼缘宽厚比的增大使得卷边的约束作用减弱,从而使构件承载力的提高逐渐变缓。
4)卷边高厚比的增加能有效增大卷边对翼缘板的约束作用,限制翼缘板的变形,从而使得构件的承载力提高。
5)结合大量有限元参数分析,提出了基于直接强度法的偏压构件弯矩-轴力关系式,该公式能较好地预估冷弯薄壁型钢偏压构件分别在以畸变失稳和腹板局部失稳为主的破坏模式下的极限承载力。
参考文献:
[1] WINTER G. Strength of thin steel compression flanges [J]. Transactions of the American Society of Civil Engineers, 1947, 112(1): 527-554.
[2] MULLIGAN G P, PEKZ T. Local buckling interaction in cold-formed columns [J]. Journal of Structural Engineering, 1987, 113(3): 604-620
[3] 何保康, 蔣路, 姚行友,等.高强冷弯薄壁型钢卷边槽形截面轴压柱畸变屈曲试验研究[J].建筑结构学报, 2006, 27 (3): 10-17.
HE B K, JIANG L, YAO X Y, et al. Experimental study on distortional buckling of high strength cold-formed steel lipped channel columns under axial compression [J]. Journal of Building Structures, 2006, 27(3):10-17. (in Chinese)endprint
[4] 李元齊, 沈祖炎, 姚行友, 等. 高强冷弯薄壁型钢卷边槽形截面轴压构件畸变屈曲控制试验研究[J]. 建筑结构学报, 2010, 31(11): 10-16.
LI Y Q, SHEN Z Y, YAO X Y, et a1. Experimental study on distortional buckling contro1 for high-strength cold-formed thin-walled steel lipped channel columns subject to axial compression [J]. Journal of Building Structures, 2010, 31(11): 10-16. ( in Chinese)
[5] YAN J, YOUNG B. Column tests of cold-formed steel channels with complex stiffeners [J]. Journal of Structural Engineering, 2002, 128(6): 737-745.
[6] YANG D, HANCOCK G J. Compression tests of high strength steel channel columns with interaction between local and distortional buckling [J]. Journal of Structural Engineering, 2004, 130(12): 1954-1963.
[7] 宋延勇. 冷弯薄壁型钢偏压构件及自攻螺钉连接承载力试验研究[D]. 上海:同济大学,2008.
SONG Y Y. Experimental study on behavior of cold-formed steel eccentrically compressed columns and self-drilling screw connections [D]. Shanghai: Tongji University, 2008. (in Chinese)
[8] 李元齐, 刘翔, 沈祖炎, 等. 高强冷弯薄壁型钢卷边槽形截面偏压构件试验研究及承载力分析[J]. 建筑结构学报, 2010, 31(11):26-35.
LI Y Q, LIU X, SHEN Z Y, et al. Experimental study and load-carrying capacity ana1ysis of eccentrica1ly-compressed on high-strength cold-formed thin-walled steel lipped channel columns [J]. Journal of Building Structures, 2010, 31(11): 26-35. (in Chinese)
[9] TORABIAN S, ZHENG B F, SCHAFER B W. Experimental response of cold-formed steel lipped channel beam-columns [J]. Thin-Walled Structures, 2015, 89(4): 152-168.
[10] 程睿, 崔佳, 金声, 等. 冷弯薄壁卷边槽钢绕弱轴偏心受压构件承载力试验研究[J]. 建筑结构学报, 2016, 37(7):74-81.
CHENG R, CUI J, JIN S, et al. Experimental study on behavior of lipped channel beam-columns in axial compression and minor-axis bending [J]. Journal of Building Structures, 2016, 37(7): 74-81. (in Chinese)
[11] 王春刚.单轴对称冷弯薄壁型钢受压构件稳定性能分析与试验研究[D]. 哈尔滨:哈尔滨工业大学, 2007.
WANG C G. Stability behavior analysis and experimental study on single-symmetric cold-formed thin-walled steel members under compression loading [D]. Harbin: Harbin Institute of Technology, 2007. (in Chinese)
[12] TORABIAN S, ZHENG B F, SCHAFER B W. Direct strength prediction of cold-formed steel beam-columns [R]. Baltimore: Johns Hopkins University, 2013: 13-72.
[13] DUBINA D, UNGUREANY V. Effect of imperfections on numerical simulation of instability behaviour of cold-formed steel members [J]. Thin-Walled Structures, 2002, 40(3): 239-262.
[14] North American specification for design of cold-formed steel structural members: S136-12 [S]. Mississauga: CSA Group, 2012.endprint

