小学数学思维策略研究
朱秀芸
应当着重培育学生精良的思维模式,训练学生敏锐准确的分析判断能力,提升学生的数学素养。
一、概念化策略
概念化策略指的是当研究对象中的某些要件回环交错时,头绪复杂,不妨把这些要件的性质划归到一个相对集中的抽象而明确的概念里,通过对整体概念的全局把握,删繁就简,抓住要害,使问题迎刃而解。概念化的过程摒除了一些非本质的条件,突出本质条件。因此,常常会使问题朝着简洁明朗的方向得以解决。
概念化策略具体操作形式为:对分散繁复的要件进行归纳抽象处理,然后进行宏观逻辑推理,最后根据结论得出实际问题的解答。思维流程图如下: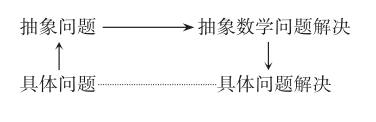
即把具体案例概念化成数学模型,对后者进行理论推演得出粗放型结论,再精细化解决问题。列方程解决问题就是典型的概念化过程。下面提出一个方程解题的例题:某工地原有一批水泥,又运来25袋,用掉34袋后,还剩41袋,这个工地原有水泥多少袋?
解题过程是:设工地原有水泥x袋(用符号代表未知数)x+25-34=41(抽象出运算问题)x=50(得出数学问题的解)
答:原来有水泥50袋(解决具体问题)。上述过程演绎了“模型思路”,即从现实生活情境中提取数量关系,形成模型,用数学符号建立方程,通过解方程,得出实际问题的最后结果。
教师在教学时要懂得运用思维策略,并且善于把这种策略让学生掌握。应对实际题型的根本策略就是生活问题数学化,通过对数学模型的处理,从抽象问题入手解决实际问题。
二、退化策略和质化策略
退化策略是指当面对整体情势难以突破时,可以退化到问题的初始状态从浅层次问题入手,待取得“进展”后再通过类比迁移,如法炮制,解决整体问题。例如,把三维空间转化成二维空间,把二维空间转化为一维空间,将不规则的组合图形切分拆散成规则图形,各个击破。
以圆柱体侧面积求法为例,这是一个典型的退化策略。圆柱体的侧面是一个立体曲面,研究前,先将其展开(退化)成一个二维平面,再依据矩形的面积公式计算其面积,然后根据长(宽)圆柱体的高,宽(长)圆柱体的底面周长,得出圆柱体的侧面积,上述推理过程就是退化策略。
质化策略指的是单独研究条件和结论,找出条件和结论之间的逻辑主线,把各种支线枝干汇聚为一个思考路径,从而使解决问题的方法清晰明朗。例如,一列火车,穿过一座铁桥,火车有200节车厢,每节车厢长4米,铁桥长900米,火车穿过铁桥时每秒行驶100米,火车穿过铁桥需要多长时间?
乍一看题目,条件较为散乱,头绪复杂。此时不妨应用质化策略,先抠住关键条件“火车每分钟行进65米”,再来仔细研究问题“穿过大桥需要多久”,综合考虑,思路就会明朗:。然后再将所有的条件归为二类,一类用来求出速度,一类用来求出路程。在求出路程的时候,将火车看作一个整体,只考虑上桥和出橋时与桥身的距离(火车全长+桥长),然后套用时间公式就可以得到结果。
三、转化策略
从信息处理的角度看,解决问题的整个进程实际上相当于一个捕捉信息加工信息输出意见的过程。信息可以以不同的形式载入,(语言、符号、图片),在加工信息时,一种形式的信号加工受阻可以设法转换形式,进行另一番加工,从而解决问题。小学数学中解题时常见的信号转换模式有:语言信号字符信号(如列方程等);语言信号图片信号(如画线段示意图);图片信号字符信号(用分数表示阴影图形)。在小学数学解题思路中,这种信号转换模式大量存在。比如,应用题都是语言信号,解答时就有必要将语言文字信号转译成字符信号,再进行信息加工;用“分数”表示几何图形的选取部分,是把图形信号转译为数码信号;如“行程问题”“工程问题”等,有时为了直观便捷,会将其转化为线段图,这是把语言信号转译为图形信号。所谓的“数形结合”思想,其实就是图形与数码信号之间的“同声传译”。
综上所述,思维策略的总体思路是将陌生问题纳入到熟悉领域内考虑。关于各种思维策略的具体操作,要根据题型不同而相机处理。可见,在小学数学教学中渗透灌输思维策略,对于培养学生科学素养,训练逻辑思维能力意义重大。(作者单位:江西省赣州市南康区第一小学)endprint

