汾河二库RCC重力坝应急除险加固后多场耦合三维有限元分析

方卫华，王润英，许珉凡

（1.水利部南京水利水文自动化研究所，江苏南京，210012；2.河海大学水利水电学院，江苏南京，210098）

1 概述

汾河二库位于太原市尖草坪区与阳曲县交界的悬泉寺，下游距太原市区30 km，是汾河上游干流上一座具有综合效益的大（2）型水利枢纽工程。枢纽工程由拦河大坝、供水发电洞和水电站组成。其中河床坝基为寒武系凤山组岩层，上部为竹叶状白云岩和薄层及中厚层白云岩，其表层为灰色白云质页岩、竹叶状白云岩互层与条带状含泥白云岩，该层层厚为9.03 m，其中灰色白云质页岩、竹叶状白云岩互层发育在上部，厚约1.5～2.0 m。坝址岩层主要为寒武系上统凤山组和奥陶系下统，透水性微弱。

2007年7 月汾河二库主体工程验收时，遗留的工程有：部分固结灌浆工程、部分帷幕灌浆工程、全部接触灌浆工程及并缝灌浆工程、坝体排水工程。

2014年开始进行以坝肩帷幕灌浆、坝基固结灌浆和坝后连续墙等施工为主的应急除险加固。

汾河二库拦河大坝为碾压混凝土重力坝，考虑到大坝除险加固实施中河床溢流坝段并缝灌浆、坝基地下连续墙及固结灌浆结构空间特性，对河床溢流坝段建立三维有限元模型，分析其加固后正常蓄水位工况条件下的结构性态，评价除险加固工程的效果，为水库正常运行提供决策依据。

2 数值计算方法及计算软件选择

2.1 应力场、位移场求解的基本理论

考虑渗流场、应力场、位移场三场耦合，鉴于规范[1]中混凝土重力坝的应力控制标准基于考虑静水压力、动水压力、扬压力等水荷载作为外力的情况，对应的方式为以材料和水的混合体作为研究对象，考虑总应力状态。这种情况下以应力分量和位移分量表示的渗流场、应力场、位移场耦合的微分方程分别如式（1）和式（2）所示：

式中：σij为总应力张量，以拉应力为正；γc为坝体材料或基岩的饱和容重；Fi为自重以外、包含水压荷载的外荷载i=x,y,z；为剪切模量 ；为 Laplace算子 ；为体积应变。

2.2 大型方程组求解方法及软件选用

为满足计算效率和计算精度的要求，方程组求解采用改进迭代格式的逐步超松弛共轭梯度法，该迭代计算方法的系数矩阵只需要存储非零元素，节省计算机存储容量，而且求解效率高，能保证多自由度有限元计算的有效进行[2]。

2.3 基于COMSOL Multiphysics的渗流计算

2.3.1 渗流方程选择

基于Darcy定律及水流连续性方程的一般渗流偏微分方程为：

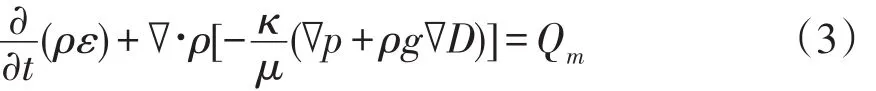
式中：ρ为流体密度；κ为渗透率；μ为流体黏度；p为压力；D为位置水头；Qm为源汇项；ε为孔隙率。

基于Rechards方程的渗流偏微分方程为：

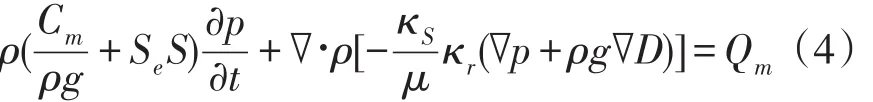
其中：Cm为容水度；Se为有效饱和度；S为储水系数；κS为饱和渗透率；κr为相对渗透率。考虑稳定渗流场，则式（4）的偏微分方程中不考虑这一项。

2.3.2 边界条件

计算稳定渗流场时，在COMSOL Multiphysics边界条件中考虑定水头边界条件和用透水层边界模拟的混合边界条件。

上下游水位以下的定水头边界条件可表达为：

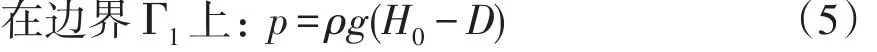
式中：H0为给定的水头；D为高程。

混合边界条件可表达为：

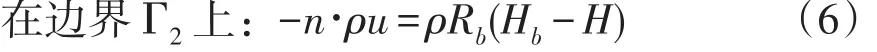
式中：Rb为传导率；Hb为外部压力水头；n为外法线方向；u为渗透压力。

由于渗流自由面及溢出点是未知的，溢出边界属于混合边界，对于复杂渗控系统处理起来较困难。非饱和渗流计算中溢出边界是一个特殊的边界条件。

采用多物理场耦合软件COMSOL Multiphysics进行渗流及多物理场耦合渗流分析。COMSOL Multiphysics是一款基于有限单元法的数值仿真软件，以一般偏微分方程或偏微分方程组为基础建立模型，具有较强的计算性能和多物理场直接耦合能力。COMSOL Multiphysics中提供的透水层边界是一种混合边界条件，并已通过若干算例验证了技术路线的合理性和可行性，可以实现对这一类边界条件的定义[3-4]。这类混合边界实际上是水头边界与流量边界的组合，求解时通过计算得到压力p的分布进行判断，基于此种情况，可以采用饱和-非饱和渗流模型及固定网格法进行迭代求解来确定混合边界条件下的渗流场。

2.3.3 坝基排水管模拟

文献[5]、[6]的计算结果表明，“以缝代井列”方法能模拟岩体排水孔幕处的流场性态，这种方法适用于排水孔间距小于6 m的排水井列。在水利水利水电工程中，排水孔间距一般都在5 m内[5]，此方法满足要求。在上述文献研究的基础上，在COM-SOL Multiphysics中将“以缝代井列”发展为“以面代井列”方法，建立模型时在排水管列的位置设置内部边界面，无需细分排水管单元，设置边界条件时将坝基排水孔幕设置为内部边界，用透水层边界条件来表达，其外部水头值取为排水井（管）口高程。

2.3.4 应力求解及标准

在COMSOL Multiphysics求解时，先用固体力学模块计算基岩在自重作用下的应力场。在坝体和坝基整体计算时，也采用固体力学模块，考虑渗流的作用，并且将采用固体力学模块计算得到的坝基应力作为整体计算时的坝基的预应力。在此基础上建立三维有限元模型应当满足SL 319-2005《混凝土重力坝设计规范》6.3.4条规定。

3 溢流坝段三维有限元分析

3.1 三维有限元模型建立

三维有限元模型中，坝基上、下游和铅直方向各取1.5倍坝高范围。针对溢流坝段除险加固后的结构特点和几何拓扑性质，模型中考虑溢流坝段的结构型式、坝体材料分区、基岩材料分区及帷幕灌浆、排水、固结灌浆的布置等因素。模型中考虑混凝土地下连续墙结构，坝基灌浆帷幕的厚度取为1.5 m。

3.2 三维有限元边界条件

渗流场计算时，上、下游水位以下取为等水头边界，其水位以上部分为混合边界，所有廊道表面为可能溢出边界，其余边界为不透水边界。

位移场、应力场计算时，坝基底部视为固定约束，坝基两侧x方向取为连杆约束，坝基及并缝灌浆高程（855.0 m）以下坝体左右岸方向（y方向）两侧取为连杆约束。

3.3 三维有限元计算参数

应力场、位移场计算时，坝体和坝基均采用塑性本构关系，屈服准则采用匹配Mohr-Coulomb准则的Drucker-Prager屈服准则，具体力学参数见表1。

下文以河床溢流典型坝段（0+099.0～0+147.2）在上游水位高程为905.7 m、下游水位高程为855.7 m、坝前淤沙高程为875.0 m的工况下为例，进行应急除险加固后的大坝安全性态分析。

3.4 溢流坝段计算结果及分析

3.4.1 渗流场

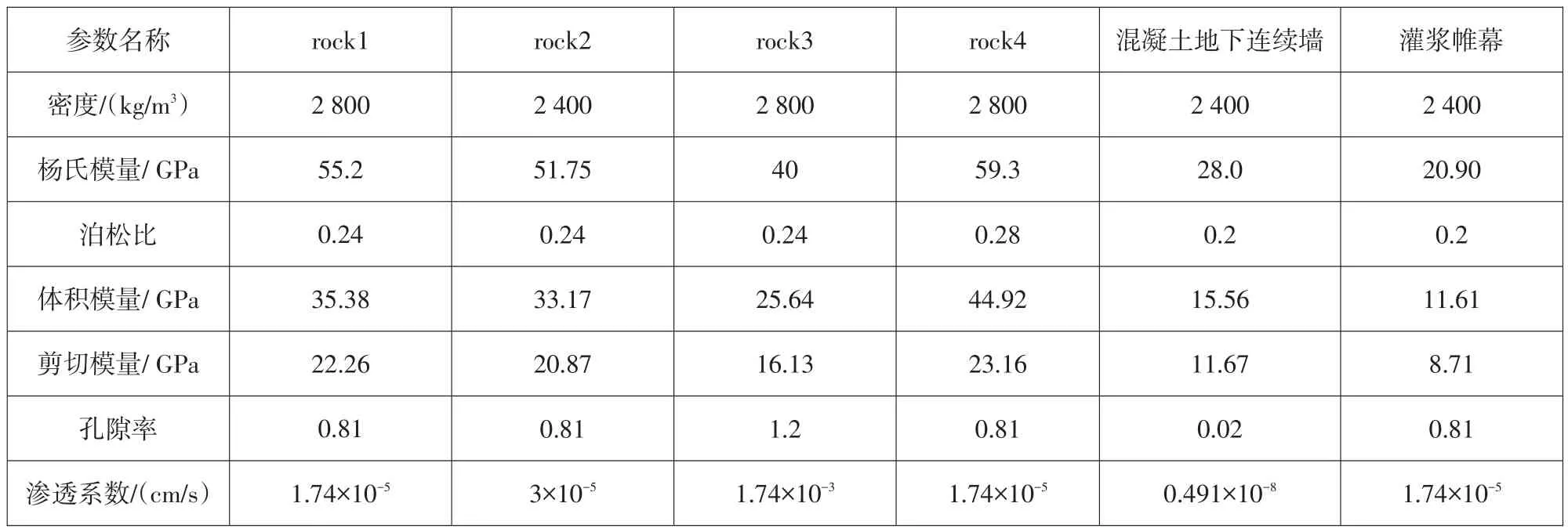
表1 坝基材料的计算参数Table 1 Calculation parameters of dam foundation materials

表2 坝基强度计算参数Table 2 Parameters of dam foundation strength calculation

除险加固之后，坝基抽排设施正常发挥作用，坝体和坝基渗流场产生变化，坝体内压力水头和坝基面渗压水头与实际值相比得到一定削减。三维有限元计算得到的渗流场等值面图见图1。

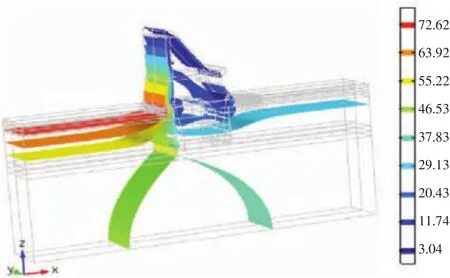
图1 渗流场压力水头等值面图Fig.1 Isopleth map of seepage field

3.4.2 位移场

图2～4为坝体x方向位移、z方向位移和总位移云图，其最大值和最小值及它们发生的位置列于表3中。结合图、表分析可知：坝体在x方向产生向下游的位移，最大值为3.92 mm，发生在堰顶，最小值为0.095 5 mm，发生在基槽下游侧坝趾处。坝体在z方向发生向下的沉降，绝对值最大为3.17 mm，发生在挑流鼻坎处；绝对值最小为0.840 mm，发生在坝体底部混凝土垫层上游侧坝踵处。总位移最大值为4.92 mm，发生在堰顶略偏下游侧；最小值为0.845 mm，发生在基槽下游侧坝趾处。

3.4.3 应力

应力以拉为正，以压为负。坝体第三主应力及垂直应力云图见图5和图6。坝体第三主应力及垂直应力最大值和最小值及它们发生的位置列于表4中。图7为垂直应力的拉应力分布示意图，图8为垂直应力局部位置拉应力分布示意图。

图2 x位移云图Fig.2 Cloud map of x-direction displacement

图3 z位移云图Fig.3 Cloud map of z-direction displacement

图4 总位移云图Fig.4 Cloud map of total displacement

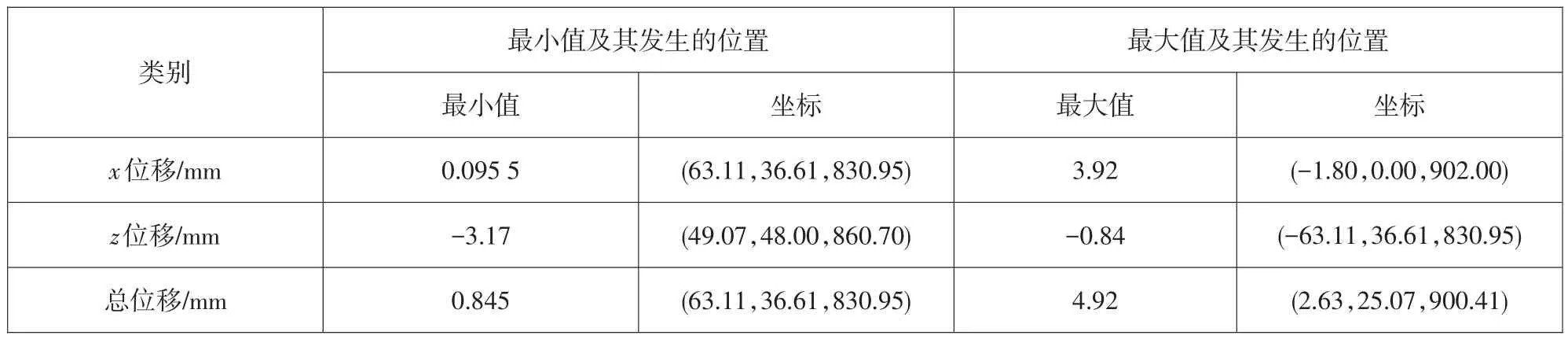
表3 工况5坝体位移最大值和最小值及其位置Table 3 Maximum and minimum displacement of dam body and their locations

图5 第三主应力云图Fig.5 Cloud map of minor principal stress

图7 垂向拉应力分布示意图Fig.7 Distribution of vertical tensile stress

图8 局部位置垂向拉应力分布示意图Fig.8 Distribution of vertical tensile stress in some components

表4 坝体应力最大值和最小值及其位置Table 4 Maximum and minimum stress of dam body and their locations

计算显示：坝体第三主应力的最小值为-5.17MPa，即最大主压应力为5.17 MPa，发生在下游廊道底部的上游侧。从图8可以看出，在廊道表面附近、上游坝踵、挑流鼻坎、反弧段、堰顶都有拉应力产生，其中，堰顶最大拉应力为0.003 85 MPa，上游坝踵处的最大拉应力为0.010 1 MPa，反弧段最大拉应力为0.098 5 MPa。

根据调查，坝基寒武系上统白云岩的饱和抗压强度为95.59～179.60 MPa，奥陶系下统白云岩的饱和抗压强度为67～239 MPa[7]；C20混凝土的轴心抗压强度标准为13.4 MPa，轴心抗拉强度标准值为1.54 MPa。坝踵部位拉应力较小，且拉应力区宽度小于坝底宽度的0.07倍且小于坝踵至帷幕中心线的距离，均满足规范要求。

4 结语

汾河二库除险加固后大坝安全性态的计算结果显示，各物理场分布基本符合相关规律，表明COMSOL Multiphysics软件可用于多场耦合分析。计算结果显示，除险加固后大部分变形、渗流和应力在合理区间内，除险加固工程基本达到预期效果。但应力场计算结果显示，在廊道表面附近、上游坝踵、挑流鼻坎、反弧段、堰顶都有拉应力产生，应加强相关区域相关物理量的安全监测（如廊道裂缝、渗流、钢筋锈蚀等的监测），进一步检验施工效果和计算的准确性。

[1]SL 319-2005,混凝土重力坝设计规范[S].

[2]林绍忠.对称逐步超松弛预处理共轭梯度法的改进迭代格式[J].数值计算与计算机应用,1997,18(4):266-270.

[3]Chui T M,Freyberg D L.The use of COMSOL for integrated hydrological modeling[C].Proc.,COMSOL Conf.2007 Boston,COMSOL AB.Newton.Mass.,2007：217-223.

[4]徐轶,徐青.基于COMSOL Multiphysics的渗流有限元分析[J].武汉大学学报(工学版),2014,47(2):165-170.

[5]王恩志,王洪涛,王慧明.“以缝代井列”——排水孔幕模拟方法探讨[J].岩石力学与工程学报,2002,21(1):98-101.

[6]杜京浓,宋汉周,霍吉祥,等.混凝土重力坝基础排水孔模拟方法对比分析[J].勘察科学技术,2015(2):9-13.

[7]水利部水利水电规划设计总院.山西省汾河二库水利枢纽工程蓄水安全鉴定报告[R].1993.