浮筒式拦污栅受力分析

袁希晨

（湖北省汉江崔家营航电枢纽管理处，湖北襄阳，441049）

0 前言

水电站上游来水中会携带大量漂浮物，如清理不及时致使杂物堵塞进水口，会加剧水头影响，导致机组频繁调整负荷直至停机，严重影响发电站的日常运行[1-2]。在进水口前增设一道浮筒式拦污栅作为进水口综合拦污系统的第一道保护，是解决此问题的一种简单、方便、经济、有效的方法。浮筒式拦污栅通常由一定数量的浮筒组成，通过钢丝绳串联成一链状，可简化为柔性结构体系[3]，一般如图1所示进行布置。目前国内文献中对浮筒式拦污栅的讨论重点多集中在设计方案与经验设计上，对其理论设计体系的研究不多[4-6]。笔者采用抛物线而非悬链线理论简化推导过程，所建的数学模型能较真实地对其受力情况进行客观反映，为实际工程设计提供一定参考。

1 钢丝绳受力分析情形假定

浮筒式拦污栅在进水口前水域中会受到极为复杂的风速、漂浮污物、水波与水流作用，受力情况会有所不同，如按结构-流体耦合综合考虑其受力情况，很难进行分析[7-9]。笔者在此对计算模型进行简化假定：（1）因其自身重量完全可被浮筒抵消，可简化为纯平面受力体系，把风速、漂浮物、水波与水流的作用力简化为直接作用于钢丝绳；（2）浮筒式拦污栅可简化为一定数量段刚体，以理想光滑钢丝绳铰联结成完全柔性机构；（3）在理论情况下存在一条能表征钢丝绳呈平衡稳定状态下的平面内折线，此平面内折线可表征其大多数情况下受载荷时的形状，在此形状下可确定唯一的受力情况；（4）参考实际漂浮物对浮筒式拦污栅的作用情况，受力情况可简化为受两组均匀分布的水平作用载荷，受力情况如图2所示。

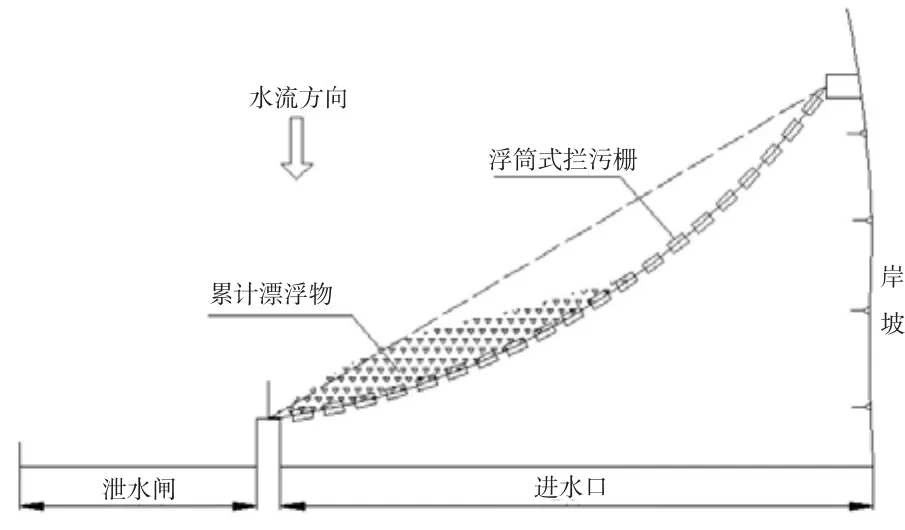
图1 浮筒式拦污栅布置图Fig.1 Layout of floating trash rack

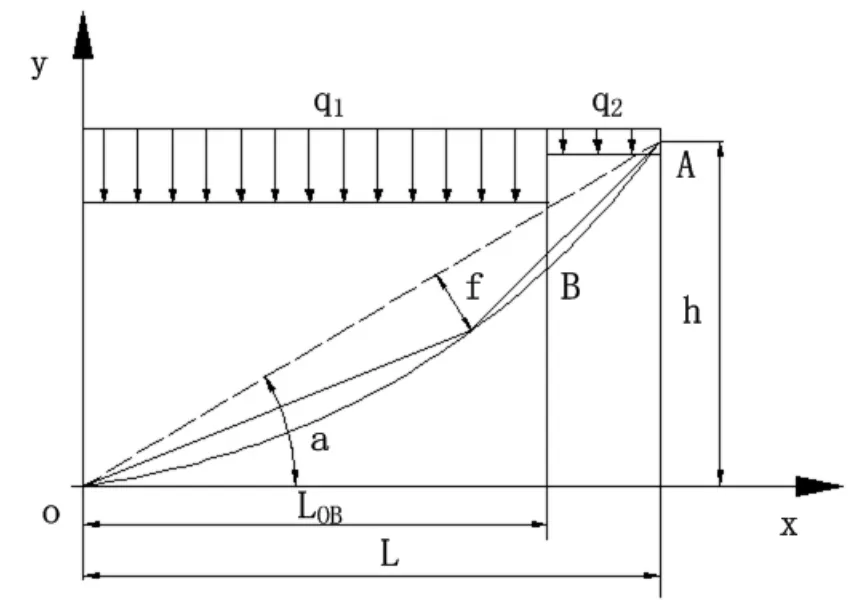
图2 浮筒式拦污栅受力示意图Fig.2 Load of floating trash rack

2 钢丝绳受力分析

2.1 钢丝绳产生的弛度与所受拉力之间的关系

在前述假定情况下，拦污栅布置于O、A点之间，因受外力的作用呈一弧形OBA状，O、A间水平距离为L，O与A连线到拦污栅上最大距离为弛度f，受q1、q2两组均匀分布的不同载荷，O点为XY坐标系的原点，O、A两点之间的y坐标为h，α为OA连线与X轴的倾角。因OB段与BA段受力不同，所以可设 y1=f1(x)表示OB段弧线，设y2=f2(x)表示BA段弧线。

在此对OB段进行单独受力分析，如图3所示，钢丝绳所受拉力为T，把T进行分解后得到水平分力H与垂直分力V，OB弧线上任意一点与X轴切线的夹角为β。因在平面力系中钢丝绳上各点受相等的水平分力，在OB段上任取一dx（0≤x≤LOB）段，在前述假定情况下，dL段所受载荷为q1dx。

图3 OB段受力示意图Fig.3 Load of OB

此时x与x+dx在Y轴的分力增量dV=dHtanβ，由受力分析可看出曲线上任一点处V=Htanβ，dV所受载荷与dx处相同，即：

对式（1）变形积分后可得OB段弧线方程y1，即，经积分为：

式中：C3、C4为积分常数。

当x=L、y=h时，由式（4）可得：

式中：C1、C2为积分常数。

当x=0、y=0时，由（2）式可得：

同上可得BA段弧线方程y2，即：

当x=L1、y1=y2时，由式（2）、（4）可得：

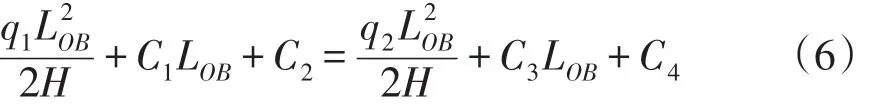
对弧线OB段与BA段分别进行受力分析，如图4所示。

OB段在受TO、TB、Q1三个作用力的情况下处于平衡状态。由前述钢丝绳受力分析情形假定（2）可知TO是向O点的切线方向，TB是在其B点沿着其切线方向，TB为作用力，T'B为反作用力，有即此点yOB'=yBA'。

对式（2）、（4）进行求导得：

当x=LOB时可得：,即：

对式（3）、（5）、（6）、（9）进行联合求解可得：

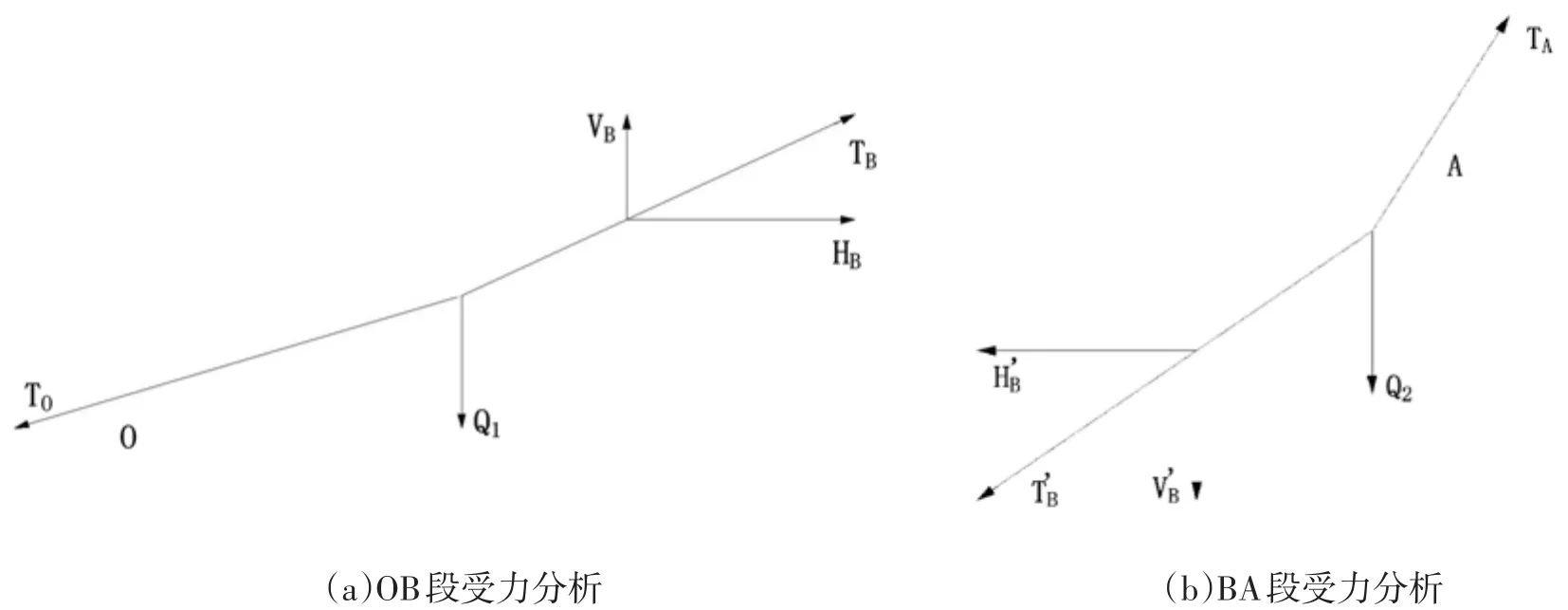
图4 OB、BA段受力分析示意图Fig.4 Load analysis of OB and BA

即可得到图2（q1≠0、q2≠0）中的弧线方程系数，但在实际工况时，由于BA段漂浮污物几乎没有，此段仅受水流作用力，可看成q1≠0、q2=0，可得OB段与BA段弧线方程，即：

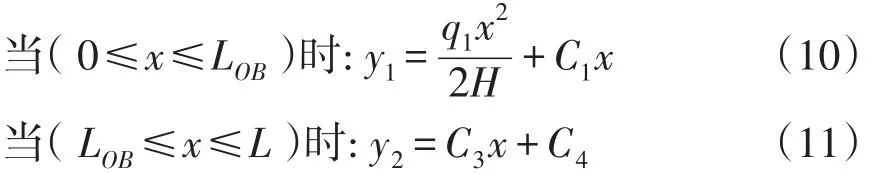
式中：

当漂浮污物累积量增多时，直线OA到弧线OBA的最大距离点会出现在OB段上，即LOB远大于L-LOB，此时

设x点处弧线的弛度为 fx，即：

如 fx有最大值，则有极值0，即，则：

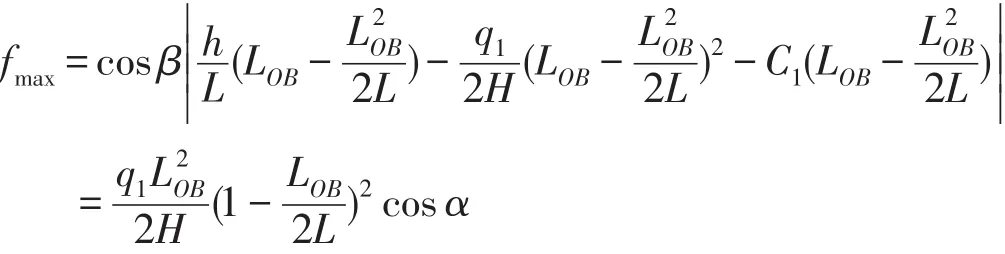
则OBA弧线上任一点所受水平分力为：

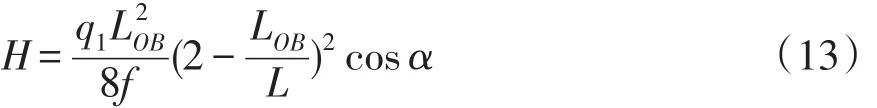
2.2 钢丝绳所受拉力

首先对弧线方程式进行求导可得其斜率，在（q1≠0、q2=0）时，将式代入OB段弧线求导方程式（7）中，可得：

由式（14）可求得OB段弧线上任一点与x轴切线的β夹角值，即：

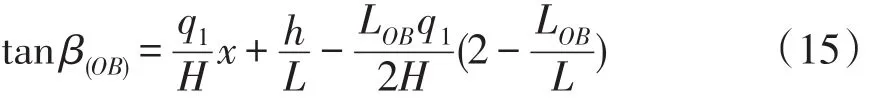
将代入BA段弧线求导方程式（8）中，可得：

此时求得图3中拉力T与其水平分力H之间关系为：

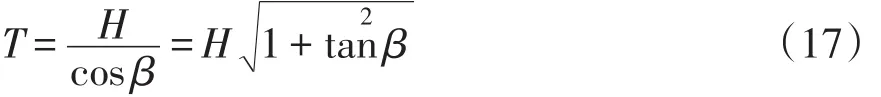
由此同样可以得到钢丝绳弧线的长度：

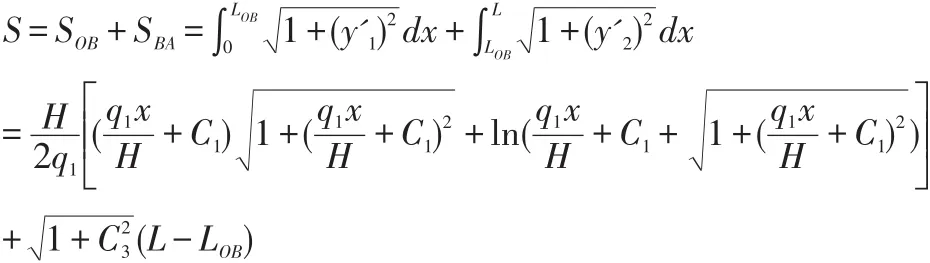
3 结语

笔者采用抛物线而非悬链线理论进行公式推导，对推导过程进行了简化，此数学模型为厂区机组正常运行、不进行弃水的正常情况下的推导，能较真实地反映其受力情况。在实际设计中可通过式（13）与式（17）进行方案优化，例如计算出受力情况后可对弧线两端固定点进行优化设计，或者通过改变弛度使弧线两端固定点受力情况得到改善。文章的讨论范围仅限于平面情况，载荷进行了简化，简化假定有待进一步讨论。通过对平面钢丝绳受力平衡状态进行讨论，可为后续考虑其结构设计、可靠性分析与疲劳寿命计算打下一定基础，为实际工程设计提供参考。

[1]任玉珊,高金花,杨敏.水电站进水口拦污栅水头损失试验研究[J].大坝与安全,2003(4):51-54.

[2]方勇耕,王俊萍.河床式水电站拦污栅堵塞调查研究[J].浙江水利水电学院学报,2004,16(3):36-38.

[3]徐远杰,杨建东,陈辉春,等.水电站进水口漂浮式拦污排张力计算[J].水利学报,2005,36(3):303-308.

[4]高朝辉,仇宝云,问泽杭.泵站拦污栅及其清污研究进展[J].排灌机械工程学报,2006,24(2):10-15.

[5]何宏斌,黄江玲.赵山渡水库漂浮物综合治理措施[J].水电能源科学,2008,26(3):120-122.

[6]许为民.浅谈拦污栅在水利工程中应用[J].科技风,2011(17):178-178.

[7]谢志强.白渔潭水电站活动拦污栅工程的施工特点[J].湖南水利水电,2006(2):4-6.

[8]周坤.水电站进水口浮式拦污排的应用与设计刍议[J].红水河,2012,31(6):5-9.

[9]于晖.浮式拦污栅设计方法的探讨[J].水利水电工程设计,2002,21(3):16-17.