基于复数神经网络求解的拟凸优化问题

李 静

(重庆工商大学 长江上游经济研究中心，重庆 400067)

非线性规划是一个目标或约束函数而不是线性的优化问题，很多现实问题都可以表示为非线性规划。在过去的几十年，针对非线性问题，学术界已经取得很大进展，求解线性和非线性优化问题的各种方法已经出现，并且已在许多领域得以实践。1986，Tank和Hopfield提出了用一个神经网络来求解线性规划问题，自那时以来，许多学者利用该领域的各项技术来解决非线性规划问题。近几年，学者们对优化神经网络进行了大量研究并取得了良好结果。例如，杨永清和曹进德[1]基于Karush-Kuhn-Tucker最优条件和投影方法构建了神经网络模型来解决不可微的非线性规划问题。刘青山和王俊[2]提出了一种单层递归神经网络来解决非光滑凸规划的线性等式约束问题。成龙等[3]用一种递归神经网络来解决带有凸不等式和线性等式约束的非光滑凸规划问题。基于吉洪诺夫正则化方法，边维和薛小平[4]提出了一种差分包络模型化的神经网络来解决线性约束非光滑凸规划问题。然而，该神经网络只能处理凸规划问题，当人们长期关注凸规划时，逐渐发现非凸规划问题的与规划问题一样重要。在非凸规划中，拟凸规划比其他非凸规划更为普遍，其应用在很多领域都有出现，如分式规划、化学、计算机视觉、生产计划和财务计划等[5]；然而，这种优化算法比凸规划困难得多。大多数神经网络不可直接用于求解凸规划，由此，学者们提出了一些新的神经网络来求解拟凸规划问题。例如，胡小林等[6]提出了一种解决神经网络伪单调变分不等式和相关的拟凸优化问题。

同时，在很多科学问题或工程问题中，会出现未知变量是复变量的情况，复变量优化问题广泛应用于交通、自适应滤波、医学影像、遥感等领域。这时，主要任务是找到相应的复变量值，进而求解优化问题。复数域不仅提供了一种简明的表示方法，而且能够保持原始问题的物理特征，因此直接利用复数解决问题的方法更优。解决复变量优化问题时，学者们通常是将复数分为实部和虚部两部分，进而将复变量优化问题转变成实变量优化问题，然后利用实数优化方法解决问题。在复数神经网络中，变量的状态、权重矢量和激活函数等均是复数，不同于实数神经网络，它具有更复杂的特性。关于复数神经网络的稳定性分析方法有很多，如Lyapunov函数法、综合法等。刘小玉、康玲芳等[7]使用综合法研究时间离散复数神经网络模型，推导出了一个确定网络参数的标准。段成军和宋乾坤[8]研究了离散时滞线性阈值神经元的复数神经网络，得到了神经网络结果的有界性、全局吸引性和全局指数稳定性的判定标准。然而，将复数神经网络应用于解决线性和非线性约束下的复数优化问题还没有受到学者们关注。因此，将复数神经网络应用于解决非线性规划下的拟凸优化问题，是一个非常有意义的研究课题。

1 预备知识

1.1 拟凸函数

以下定义和引理中Ω为n维欧式空间。

定义1[9]函数F：Rn→Rn，如果存在一个常数L，对任意的x，y∈Ω，都有‖F(x)-F(y)‖≤L‖x-y‖，其中‖·‖表示Rn上的欧几里得范数，那么F在Ω内是李普希兹连续的。

定义2 如果任意不同的x，y∈Ω都有▽f(x)(y-x)≥0⟹f(y)≥f(x)，那么可微函数f：Rn→R是在集合Ω上的拟凸函数。

引理1[10]如果可微函数f：Rn→R在集合Ω上是拟凸函数，那么x*∈Ω满足(▽f(x*))T(x-x*)≥0，∀x∈Ω，当且仅当f(x*)是f(x)在Ω内的最小值。

定义3[11]如果对任意的x，y∈Ω都有(F(x))T(y-x)≥0⟹(F(y))T(y-x)≥0，那么函数F：Rn→Rn是集合Ω上的拟单调函数。

引理2[12]一个可微函数是拟凸的，当且仅当它的梯度是一个拟单调映射。

1.2 实向量和复向量之间的转化

令z=(z1，z2，…，zn)T，即z∈Cn；由于复数不方便下文的讨论，在此将复变量函数转化为实数域上的函数。不妨令x=(x1，x2，…，xn，y1，y2，…，yn)T，其中xi，yi，i∈[1，n]分别表示zi的实部和虚部.下文的研究都建立在这个转化之上。

1.3 李雅普诺夫稳定性

考虑如下系统：

(1)

其中，f(x)=(f1(x1，x2，…，xn)，f2(x1，x2，…，xn)，…，fn(x1，x2，…，xn))T；x=(x1，x2，…，xn)T。

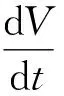
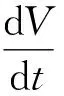
2 复数神经网络模型

2.1 模型介绍

在此引入如下神经网络模型：

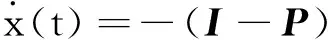
(2)

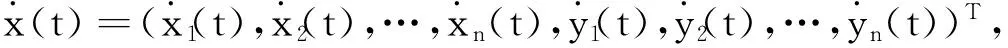
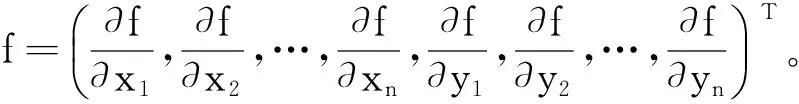
2.2 复数优化问题的转化

这里首先引入一个拟凸优化问题：

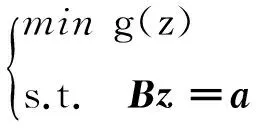
(3)

其中，z=(z1，z2，…，zn)T∈Cn，a∈Cm；目标函数g：Cn→R是一个二次可微的拟凸函数；B∈Cm×n，并且B是一个行满秩矩阵。

不妨令：

可以得出：

可以用实向量x=(x1，x2，…，xn，y1，y2，…，yn)T，xi，yi∈R来表示复向量z=(z1，z2，…，zn)T，zi∈C。

同理可以用一个实向量b来表示a，令

为了将复数优化问题转化为实数域上的优化问题，首先定义如下的辅助函数：

f(x)：R2n→R

其中f(x)=g(z)，z=x+iy.

对复数域上的拟凸优化问题(3)可以做如下变形：

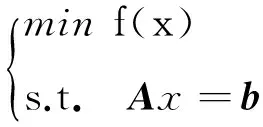
(4)

其中x=(x1，x2，…，xn，y1，y2，…，yn)T∈R2n，b∈R2m；目标函数f：R2n→R是一个二次可微的拟凸函数；A∈R2m×2n，A是一个行满秩矩阵(r(A)=2m<2n)，令

于是Ax=b等价于式(3)中的Bz=a.

到此，将一个复数域上的拟凸优化问题转化为实数域上的拟凸优化问题，后面的讨论都将建立在式(4)的基础上。

2.3 模型推导过程

由引理1可知，x*式(4)的一个最优解，当且仅当(▽f(x*))T(x-x*)≥0，∀x∈Ω={x∈R2n|Ax=b}都成立；其中Ω表示集合{x∈R2n|Ax=b}。

如果存在(x*，y*)∈R2n×R2m满足

(5)

那么，对所有的x∈Ω={x∈R2n|Ax=b}都有

由式(5)的第一个等式可以得到A▽f(x*)-AATy*=0，因为A是一个行满秩矩阵，于是AAT一定是一个可逆矩阵，那么可以推导出

y*=(AAT)-1A▽f(x*)

(6)

把式(6)代入式(5)中可以得到▽f(x*)-AT(AAT)-1A▽f(x*)=0，等价于(I-AT(AAT)-1A) ▽f(x*)=0，令P=AT(AAT)-1A，得到(I-P)▽f(x*)=0

由上述推过程，可以建立如下神经网络模型：

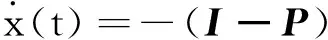
(7)

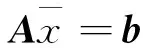
3 神经网络稳定性与收敛性证明

3.1 神经网络模型解的性质

引理3 对任意的初始点x0∈R2n，带有初值条件x(0)=x0的系统式(7)存在唯一解x(t)，以及如果x(0)=x0∈Ω，那么当t≥0时x(t)∈Ω。

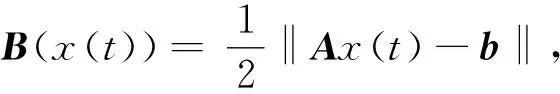
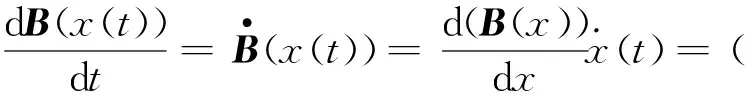
(8)

令x(t)=(x1(t)，x2(t)，…，x2n(t))T，那么

(9)

把Ax(t)，b分别记为Ax(t)=(T1，T2，…，T2m)T，b=(s1，s2，…，s2m)T，那么

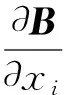
s1)，(T2-s2)，…，(T2m-s2m))T，由式(9)可知：

且Ax(t)-b=(T1-s1，T2-s2，…，T2m-s2m)T；那么

▽B(x)=AT(Ax(t)-b)

(10)

将式(10)代入式(8)，得到：

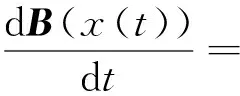
-(Ax(t)-b)TA(I-P)▽f(x(t))

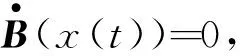
3.2 主要结论及证明

现在介绍关于神经网络式(7)收敛性及稳定性的主要结论。

定理3 对任意的初始点x0∈Ω，神经网络式(7)是李雅普诺夫全局稳定的，而且是收敛于优化问题式(4)的最优解.

证明由引理3可知，对任意的初值点x0∈Ω，在Ω中总存在唯一的局部解x(t)，即Ax(t)=b对所有的t≥0都成立。假设x*是优化问题式(4)的一个最优解，由引理2可以得到：

(▽f(x(t)))T(x(t)-x*)≥0

(11)

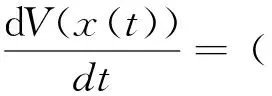
(I-P)▽f(x(t))-(x(t)-x*)T(I-P)▽f(x(t))

因为(I-P)2=(I-AT(AAT)-1A)(I-AT(AAT)-1A)=

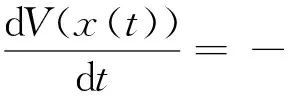
-(▽f(x(t)))T(I-P)2▽f(x(t))=-‖(I-P)▽f(x(t))‖2≤0，因此，对任意的初始点x0∈Ω，总存在唯一的满足李雅普诺夫稳定条件的全局解x(t)。

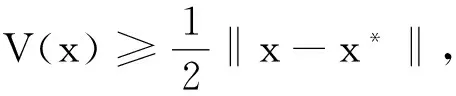
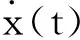
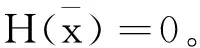
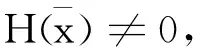
V(x(0))<∞。

本节内容虽然是建立在实数的基础上展开讨论的，但是在第2节中，进行了复数到实数的转化；也就是说把要研究的复数神经网络转化成实数神经网络。第2节中假设合理，推导过程清晰，并不会影响本节的证明，因此本节得出的实数域上的结论完全适用于本文的研究对象.

备注：根据定理3，对于任意初始点x0∈Ω，神经网络系统式(7)收敛到优化问题式(4)的最优解.但是如果初始点x0∉Ω，不能证明神经网络系统式(7)的稳定性。

4 实例验证

下面举一个例子来说明本文中得出的结论在研究复数优化问题时的有效性。

关于优化问题

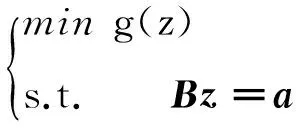
(12)

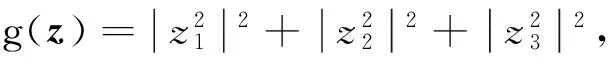
为了得出式(12)的最优解，首先要将复数优化问题转化为实值的优化问题，于是有

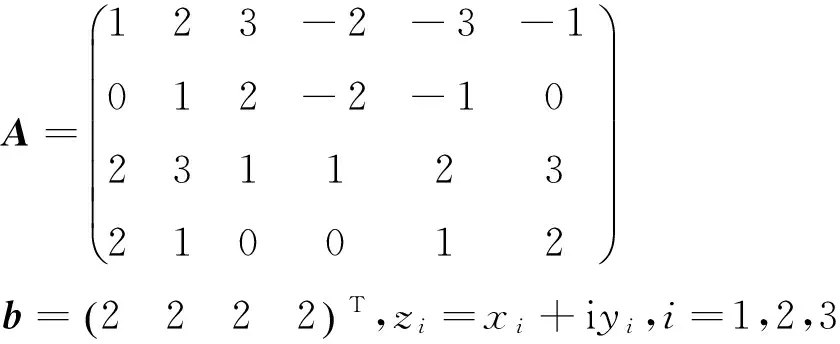
(13)

用传统方法求解上述优化问题。

因为r(A)=r(A，b)=4<6，可知非齐次线性方程组Ax=b有无穷多解，求出通解为

其中k1，k2为任意常数；因此将x代入式(13)中，得出f(x)是关于k1，k2的二元函数。

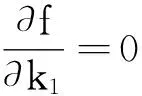
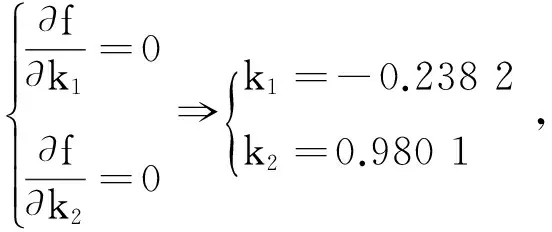
神经网络模型式(2)的解与上述方法得出的结果相同，说明本文得出的定理6是正确的。

[1]YANG Q Y，CAO J.The Optimization Technique for Solving a Class of Non-differentiable Programming Based on Neural Network Method [J].Nonlinear Analysis Real World Applications，2010，11(2)：1108-1114

[2] LIU Q S，WANG J.A One-Layer Recurrent Neural Network for Non-smooth Convex Optimization Subject to Linear Equality Constraints[C]∥International Conference on Neural Information Processing，Springer Berlin Heidelberg，2008

[3] CHENG L，HOU Z G，LIU Y Z，et al.Recurrent Neural Network for Non-Smooth Convex Optimization Problems With Application to the Identification of Genetic Regulatory Networks[J].IEEE Trans Neural Netw，2011，22(5)：714-726

[4] BIAN W，XUE X.Neural Network for Solving Constrained Convex Optimization Problems With Global Attractivity[J].IEEE Transactions on Circuits & Systems I Regular Papers，2013，60(3)：710-723

[5] BAZARAA M S，SHERALI H D，SHETTY C M.Nonlinear Programming： Theory and Algorithms[J].Journal of the Operational Research Society，1994，45(7)：846-846

[6] HU X L ，WANG J .Solving Pseudomonotone Variational Inequalities and Pseudoconvex Optimization Problems Using the Projection Neural Network[J].IEEE Transac-tions on Neural Networks，a Publication of the IEEE Neural Networks Council，2006，17(6)：1487-1499

[7] LIU X Y ，LIN F K，LIU B.A Synthesis Method Based on Stability Analysis for Complex-valued Hopfield Neural Network[C]∥Asian Control Conference，2009

[8] DUAN C J，SONG Q K.Stability，Boundedness and Stability for Discrete-Time Delayed Neural Network with Complex-Valued Linear Threshold Neurons[J].Discrete Dynamics in Nature & Society，2010(5)：1038-1045

[10] KINDERLEHRER D，STAMPACCHIA G.An Introduction to Variational Inequalities and their Applications[M].Academic Press，1980

[11] XIA Y S，LEUNG H，WANG J.A Projection Neural

Network and Its Application to Constrained Optimization Problems[J].IEEE Transactions on Circuits & Systems I Fundamental Theory & Applications，2002，49(4)：447-458

[12] KARAMARDIAN S，SCHAIBLE S.Seven Kinds of

Monotone Maps[J].Journal of Optimization Theory and Applications，1990，66(1)：37-46

[13] 马知恩，周义仓.常微分方程定性与稳定性方法[M].北京：科学出版社，2001

MA Z E，ZHOU Y C.The Method of Qualitative Theory and Stability Theory of Ordinary Differential Equations [M].Beijing：Science press，2001