一种基于区间二型模糊信息熵的TOPSIS多属性决策方法*

周熠烜， 王 熠， 平轶男， 徐立为

(安徽大学 数学科学学院，合肥 230601)

0 引 言

随着社会的进步与发展，管理决策问题已成为社会生活中不可或缺的一部分。而在实际决策问题中[1]，由于客观事物的复杂性、决策者认识上的局限性以及思维判断的模糊性，决策者很难用精确的清晰数来定量描述自己的评价，而更倾向于用“一般好”、“很好”这样定性的语言变量来描述自己的评价信息，在此基础之上，多种语言评价信息例如纯语言[2]、犹豫模糊语言[3]、二元语义模型[4]等被相继提出并应用至群决策、模式识别、工业工程等实际领域中。

语言决策中最核心的问题之一是基于语言信息的词计算。目前，绝大多数处理语言信息的方法可以分为两类。一方面，直接对语言信息进行处理，例如Herrera等和Torra提出了有序语言计算模型[5-6]，即利用语言评价集自身的顺序结构直接对语言符号进行处理。但是这类方法事先定义的语言评价集是离散的，语言信息经过运算后，很难精确对应到初始的语言评价信息集，因此会产生信息的丢失。为此，Herrera等提出了二元语义的计算模型[4，7]，将语言短语看作在其定义域内是连续的，以预定的语言短语集合中的短语和一个数值的形式来表示语言评价信息运算后所获得的所有信息，这样能尽可能地确保原始语言信息的完整与真实。另一方面，是将语言评价信息转化为模糊数。对于语言评价信息取语义函数后，一般得到的还是一个确定的值，因此不能很好地反映语言评价信息本身具有的不确定性。而将语言评价信息转化为模糊数之后，由于模糊数本身具有的隶属度关系，使得语言评价信息保持其原有的模糊性。常见的模糊数有区间模糊数、三角模糊数和梯形模糊数。梯形模糊数在适当的条件约束下可以转化为区间模糊数和三角模糊数。

考虑实际生活中的语言评价信息的复杂性以及多样性，某些语言评价信息并不能用简单的语言术语集来定性地刻画。为此，Mendel教授基于社会语言短语调查[8-9]，将生活中常用的几十个语言评价短语通过EKM算法[10]转化成区间二型模糊集，对区间二型模糊集进行运算后，通过二型模糊逻辑控制器再将最终运算结果还原成普通的语言评价短语。这种方法既保留了原始语言信息的真实性和完整性，还使评价过程和评价结果极其符合实际生活中的语言规则，因此得到了广泛的应用[11]。

TOPSIS方法是一种常用的多目标决策分析方法，是由Hwang 和Yoon[12]于1981 年首次提出，TOPSIS 法是在现有的对象中根据有限个评价对象与最优化目标的接近程度进行排序的方法。Chen[13]提出了基于区间二型模糊数的TOPSIS方法。该方法是通过假设一个正理想方案和一个负理想方案，然后分别确定所提出的方案与正、负理想方案的符号距离。根据符号距离的大小对各方案排序，距离正理想解最近且远离负理想解即为最好方案，由此得到综合评价结果。熵权法是根据各项指标观测值所提供的信息量大小来确定权重的方法，是以决策者预先确立的偏好权数为基础，将决策者的主观判断与目标机的固有信息结合起来，实现主客观的统一。

在实际决策过程中，TOPSIS法中会出现依赖于专家直接给出的权重而失去了客观性的问题。为了克服上述缺点，结合熵权法以及区间二型模糊数本身的一些性质特点，将熵权法拓展到区间二型模糊多属性决策中，给出一种基于改进的区间二型模糊信息熵的TOPSIS多属性决策方法，运用熵权法计算出权重，再用TOPSIS方法进行多属性决策。该方法有利于横向和纵向比较，充分利用原始数据提供的信息，减少主观因素对评价结果的干扰，而且要求实施简单，可以量化评价结果。该方法不仅拓展了传统熵权法的应用范围，而且为区间二型模糊TOPSIS 决策开辟了一条新的道路，使决策者可以直接利用评估信息来做出决策，为决策者提供了便捷，也使得区间二型模糊TOPSIS 方法能更好地应用于实践。

1 基本概念

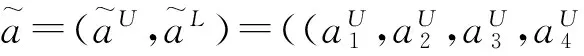
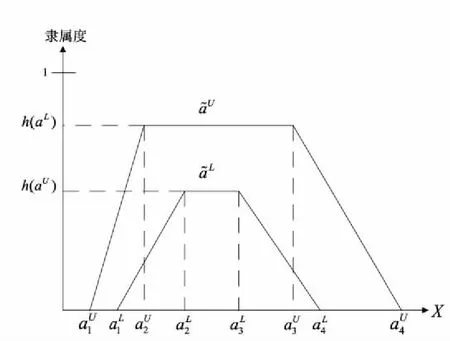
图1 区间二型模糊数Fig.1 Interval type-2 fuzzy number

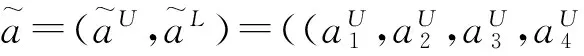
(1) 加法运算：

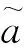
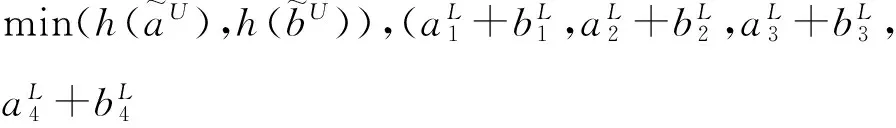
(2) 减法运算：

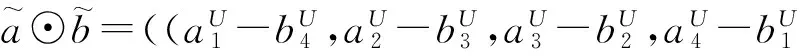
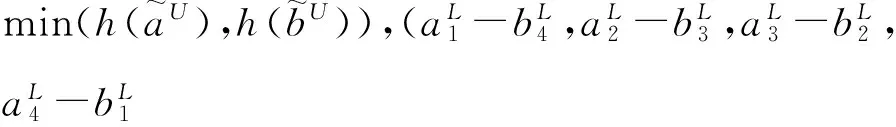
(3) 乘法运算：

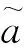
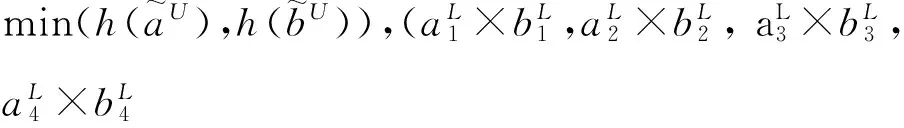
(4) 数乘运算：

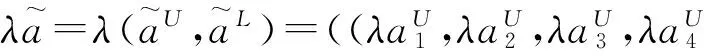
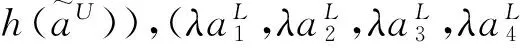
(5) 除法运算：

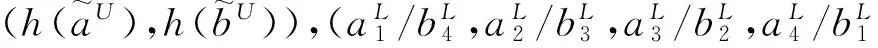
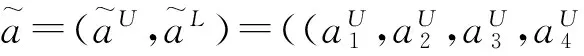
(1)

(2)

2 区间二型模糊信息熵

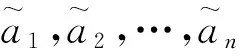
(3)

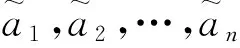
(4)

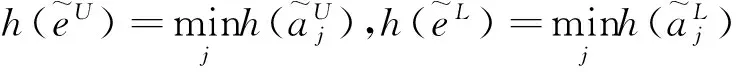
(5)

根据文献[13]，若决策者给出语言变量，则可利用表1中的对应关系，将语言术语转化为区间二型模糊数。

由表1可以看出，语言决策变量转化为区间二型模糊数之后的每个元素均属于闭区间[0，1]，为方便起见，所讨论的区间二型模糊数均指由表1的转化规则转化成的区间二型模糊数，即其所有元素均在[0，1]内，故针对定义3，区间二型模糊信息熵具有下述性质。

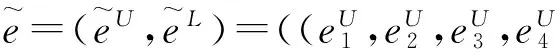
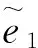
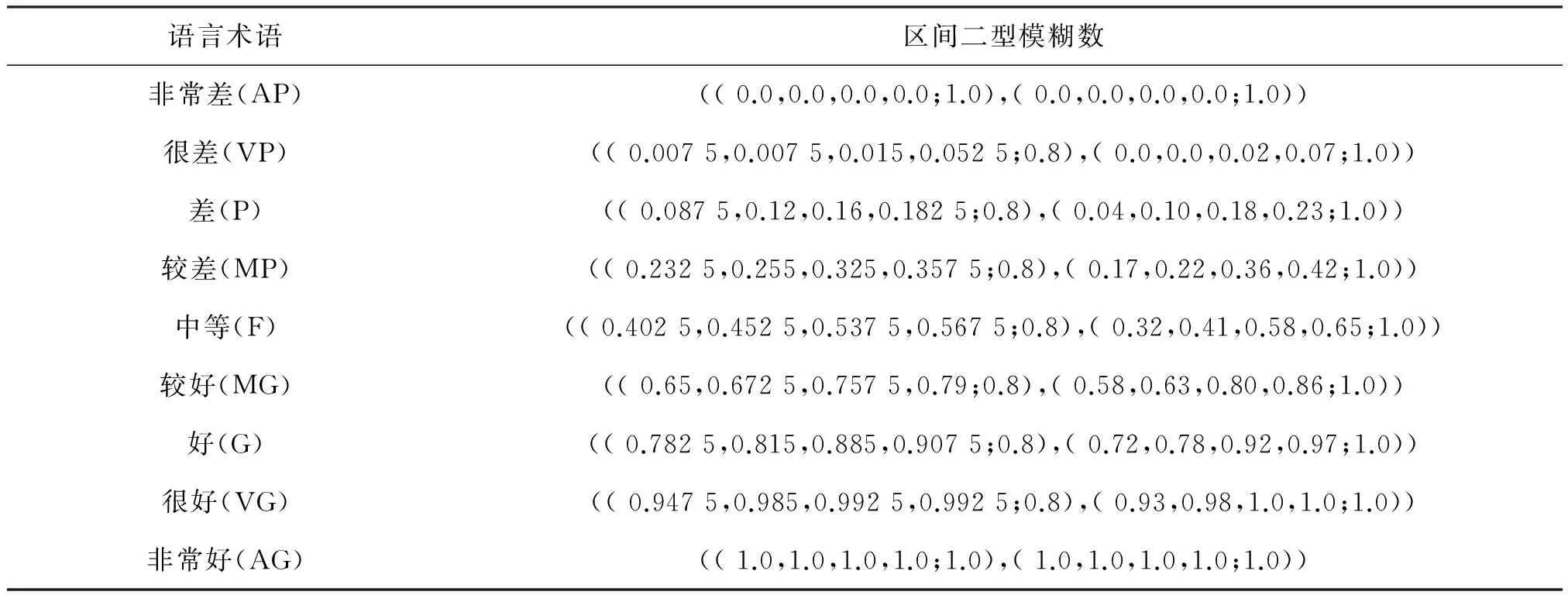
表1 语言术语与其相应的区间二型模糊数Table 1 Linguistic terms and their corresponding interval type-2 fuzzy number

3 TOPSIS多属性决策方法分析

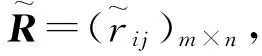
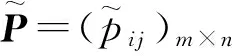
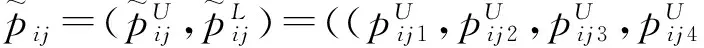
(6)

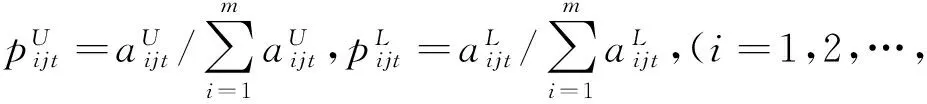
(7)

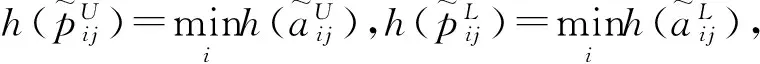
(8)

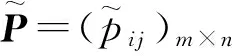
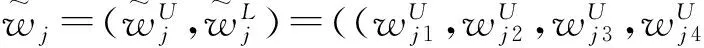
(9)

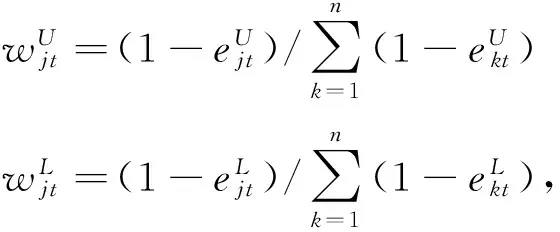
(10)

(11)

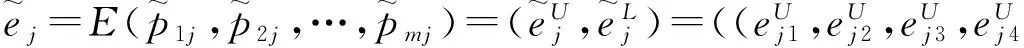
由式(4)和式(5)确定。

为了构建新的TOPSIS多属性决策方法，下面定义两类符号距离矩阵。

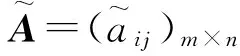
(12)

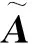
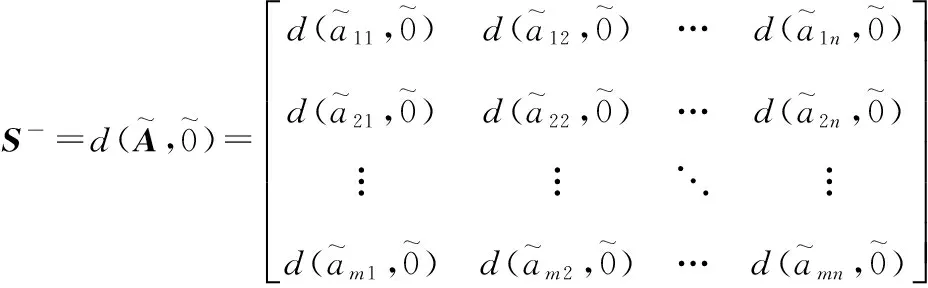
(13)

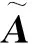
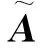
(14)

和加权负符号距离矩阵：

(15)

定义7 称

(16)

为方案xi的贴近度系数。

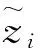
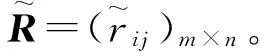
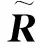
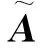
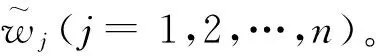
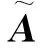
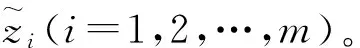
Step7 计算

(17)

同时根据yi的大小对方案xi(i=1，2，…，m)进行排序并择优。

Step8 结束。

4 案例分析

应急物资储存点的选择是应急救援管理的重要问题之一，假设某城市需要从5个备选地x1，x2，x3，x4，x5中选取一个作为应急物资的储存点，现依据4个属性来进行评价，包括地理位置(c1)、储存成本(c2)、建筑结构(c3)和环境状况(c4)。

设专家根据语言集S={AP，VP，P，MP，F，MG，

G，VG，AG}对这5个方案进行评价，得到语言决策矩阵：

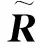
由式(17)知：

故有y5>y3>y2>y4>y1，即x5>x3>x2>x4>x1，最优方案为x5。

相比较于文献[13]来说，笔者在构建区间二型模糊TOPSIS多属性决策方法时，并没有直接给出属性权重，而是通过构建各个属性的区间二型模糊信息熵来获取区间二型模糊属性权重，使得该区间二型模糊TOPSIS多属性决策方法更具有客观性和可靠性，也使得决策结果更具有说服力。

5 结束语

给出了一种新的基于区间二型模糊信息熵的TOPSIS多属性决策方法，与传统的TOPSIS方法相比，优点在于通过定义新的区间二型模糊信息熵来构建区间二型模糊属性权重，这使得决策结果更加客观和有效。在未来的研究中，可以进一步将该方法拓展至其他语言环境中[14-15]，例如二元语义、犹豫语言等，并做进一步的比较研究，同时，还可以应用于教师职称审核、组合预测研究、网络基金评审等社会活动中。

[1] 徐泽水.不确定多属性决策方法及应用[M].北京：清华大学出版社，2004

XU Z S.Uncertain Multiple Attribute Decision Making：Method and Applications [M].Beijing： Tsinghua University Press，2004

[2] ZADEH L A，The Concept of a Linguistic Variable and Its Application to Approximate Reasoning-I[J].Information Science，1975，8：199-249

[3] DODRIGUEZ RM，MARTINEZ L，HERRERA F.Hesitant Fuzzy Linguistic Term Sets for Decision Making[J].IEEE Transaction Fuzzy Systems，2012，20： 109-119

[4] HERRERA F，MARTíNEZ L.A Model Based on Linguistic 2-tuple for Dealing with Multigranular Hierarchical Linguistic Contexts in Multi-expert Decision Making [J].IEEE Tran-sactions on Systems，Man and Cybernetics，Part B： 2001，31： 227-234

[5] HERRERA F，HERRERA-VIEDMA E，VERGEGAY J L.Direct Approach Processes in Group Decision Making Using Linguistic OWA Operators [J].Fuzzy Sets and Systems，1996，79： 175-190

[6] TORRA V.Negation Functions Based Semantics for Order-ed Linguistic Labels [J].International Journal of Intelli-gent Systems，1996，11： 975-988

[7] MERIGó J M，GIL-LAFUENTE A M，Induced 2-tuple Ling-uistic Generalized Aggregation Operators and Their App-lication in Decision-Making [J].Information Sciences，2013，236： 1-16

[8] MENDEL J M，JOHN R I，LIU F L.Interval Type-2 Fuzzy Logical Systems Made Simple [J].IEEE Transactions on Fuzzy Systems，2006，14： 808-821

[9] LIU F，MENDEL JM.Encoding Words into Interval Type-2 Fuzzy Sets Using an Interval Approach [J].IEEE Transac-tions on Fuzzy Systems，2008，16： 1503-1521

[10] KARNIK N N.MENDEL J M.Operations on Type-2 Fuzzy Sets [J].Fuzzy Sets and Systems，2001，122： 327-348

[11]MENDEL J M，WU D.Perceptual Computing： Aiding People in Making Subjective Judgments [M].New Jer-sey：IEEE - Wiley Press，Piscataway，2010

[12]HWANG C L，YOON K.Multiple Attribute Decision Making： Method and Application，a State of the Art Survey [M].Berlin： Spring2Verlag，1981，1-7

[13] CHEN T Y.Signed Distanced-Based TOPSIS Method for Multiple Criteria Decision Analysis Based on Generalized Interval-Valued Fuzzy Numbers [J].International Journal of Information Technology & Decision Making，2011(5)：51-54

[14] 吴群，吴澎，周礼刚.基于联系数的区间二元语义模糊多属性群决策方法[J].重庆工商大学学报(自然科学版)，2016，33(1)： 1-8

WU Q，WU P，ZHOU L G.Interval 2-tuple Linguistic Fuzzy Multiple Attributes Group Decision-making Based on Connection Variables [J].Journal of Chongqing Tech-nology and Business University (Natural Science Edi-tion)，2016，33(1)： 1-8

[15] 吴群，吴澎，周元元，等.2TLCGPOWA算子及其在多属性群决策中的应用[J].计算机工程与应用，2017，53(3)： 47-53

WU Q，WU P，ZHOU Y Y，et al.Generalized 2-Tuple Linguistic Connection Power Ordered Weighted Average Operator and Its Application to Multiple Attribute Group Decision Making [J].Computer Engineering and Applications，2017，53(3)： 47-53